唐先智，王 波，楊樹軍，邸立明，夏懷成

(燕山大學(xué)車輛與能源學(xué)院，秦皇島 066004)

2016043

基于狀態(tài)轉(zhuǎn)移概率的混合動(dòng)力客車控制策略*

唐先智，王 波，楊樹軍，邸立明，夏懷成

(燕山大學(xué)車輛與能源學(xué)院，秦皇島 066004)

建立了混合動(dòng)力客車的數(shù)學(xué)模型，以及動(dòng)態(tài)規(guī)劃的目標(biāo)函數(shù)、狀態(tài)轉(zhuǎn)移方程和迭代方程。提出基于狀態(tài)轉(zhuǎn)移概率的混合動(dòng)力客車動(dòng)態(tài)規(guī)劃控制策略。基于狀態(tài)轉(zhuǎn)移概率對駕駛循環(huán)工況進(jìn)行預(yù)測，使動(dòng)態(tài)規(guī)劃迭代過程中狀態(tài)轉(zhuǎn)移的燃油消耗為基于車速狀態(tài)轉(zhuǎn)移概率的加權(quán)平均值。改進(jìn)后的控制策略可用于實(shí)時(shí)在線控制，無需預(yù)先得知駕駛循環(huán)工況，提高了動(dòng)態(tài)規(guī)劃的實(shí)時(shí)應(yīng)用能力。臺架試驗(yàn)結(jié)果表明，改進(jìn)后的控制策略可以在線對發(fā)動(dòng)機(jī)和電機(jī)所需轉(zhuǎn)矩進(jìn)行合理分配，使電池的電荷狀態(tài)處于平衡狀態(tài)且換擋平穩(wěn)，優(yōu)化了發(fā)動(dòng)機(jī)工作點(diǎn)，提高了整車的燃油經(jīng)濟(jì)性。

混合動(dòng)力汽車；狀態(tài)轉(zhuǎn)移概率；動(dòng)態(tài)規(guī)劃；控制策略

前言

整車控制策略是混合動(dòng)力汽車研究的核心內(nèi)容之一，其控制效果的好壞直接影響混合動(dòng)力汽車的性能。最優(yōu)控制是國內(nèi)外學(xué)者重點(diǎn)研究的內(nèi)容，其中，動(dòng)態(tài)規(guī)劃是解決離散最優(yōu)控制問題最常用的算法。理論上，動(dòng)態(tài)規(guī)劃可達(dá)到最優(yōu)控制，但目前在混合動(dòng)力汽車整車控制的研究領(lǐng)域里，主要用于對門限值控制策略的控制門限進(jìn)行優(yōu)化和作為控制效果的基準(zhǔn)對其他控制策略進(jìn)行評價(jià)，并沒有直接應(yīng)用到整車控制中[1-7]，其主要原因是，動(dòng)態(tài)規(guī)劃是一種逆序計(jì)算方法，迭代從末端開始，到始端為止，逆向遞推，因此需要提前預(yù)知車輛的駕駛循環(huán)工況，這在車輛實(shí)際運(yùn)行過程中很難做到，所以限制了該算法在整車控制中直接在線實(shí)時(shí)應(yīng)用[8-10]。

本文中提出基于狀態(tài)轉(zhuǎn)移概率的混合動(dòng)力客車動(dòng)態(tài)規(guī)劃控制策略。臺架試驗(yàn)表明，改進(jìn)后的控制策略可以在線實(shí)時(shí)對整車進(jìn)行控制，提高了動(dòng)態(tài)規(guī)劃的實(shí)時(shí)應(yīng)用能力，控制效果好，可改善整車的燃油經(jīng)濟(jì)性。

1 混合動(dòng)力客車建模

1.1 混合動(dòng)力客車結(jié)構(gòu)與參數(shù)

本文中以某混合動(dòng)力客車為研究對象，其整車結(jié)構(gòu)如圖1所示，具體參數(shù)如表1所示。

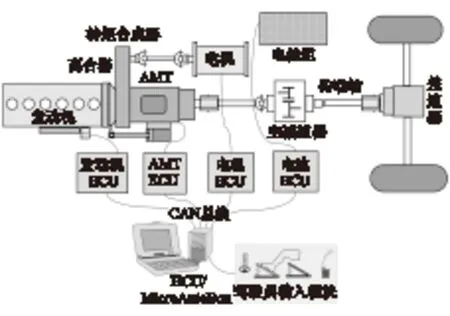
圖1 混合動(dòng)力客車整車結(jié)構(gòu)示意圖

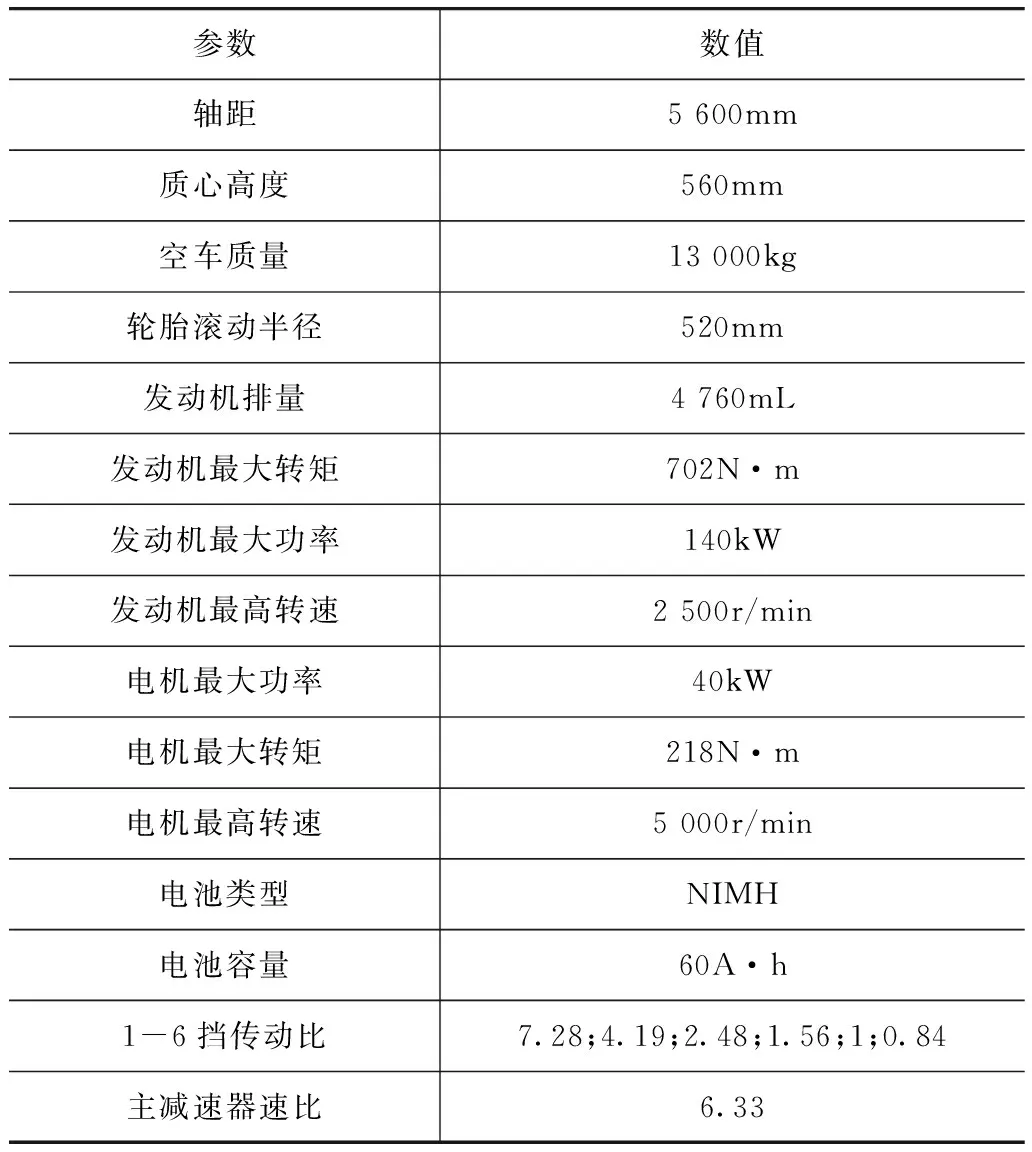
參數(shù)數(shù)值軸距5600mm質(zhì)心高度560mm空車質(zhì)量13000kg輪胎滾動(dòng)半徑520mm發(fā)動(dòng)機(jī)排量4760mL發(fā)動(dòng)機(jī)最大轉(zhuǎn)矩702N·m發(fā)動(dòng)機(jī)最大功率140kW發(fā)動(dòng)機(jī)最高轉(zhuǎn)速2500r/min電機(jī)最大功率40kW電機(jī)最大轉(zhuǎn)矩218N·m電機(jī)最高轉(zhuǎn)速5000r/min電池類型NIMH電池容量60A·h1-6擋傳動(dòng)比7.28;4.19;2.48;1.56;1;0.84主減速器速比6.33

1.2 混合動(dòng)力客車建模

由于本文中不涉及車輛動(dòng)力學(xué)的研究，只研究系統(tǒng)內(nèi)部變量之間的關(guān)系，故將車輛模型簡化為靜態(tài)離散數(shù)學(xué)模型：

(1)

式中：v(k)為k時(shí)刻車速，km/h；v(k+1)為k+1時(shí)刻車速，km/h；M為車輛質(zhì)量，kg；rd為車輪半徑，m；Twh,k為k時(shí)刻車輪轉(zhuǎn)矩，N·m；Fr為滾動(dòng)阻力，N；Fa為空氣阻力，N。

Twh,k=TxRdηd

(2)

式中：Tx為變速器輸出轉(zhuǎn)矩，N·m，x為變速器擋位，x=1,2,…,6；Rd為主減速器速比；ηd為主減速器傳動(dòng)效率。

Tx=Rxηx(Te+TmRcηc)

(3)

式中：Rx為變速器傳動(dòng)比；ηx為變速器傳動(dòng)效率；Te為發(fā)動(dòng)機(jī)轉(zhuǎn)矩，N·m；Tm為電機(jī)轉(zhuǎn)矩，N·m；Rc為轉(zhuǎn)矩合成器速比；ηc為轉(zhuǎn)矩合成器傳動(dòng)效率。

本文中不考慮發(fā)動(dòng)機(jī)的動(dòng)態(tài)特性，因此發(fā)動(dòng)機(jī)的燃油消耗靜態(tài)數(shù)學(xué)模型可通過實(shí)驗(yàn)法簡化為

Wfuel=Wfuel(Te,ωe)

(4)

式中：Wfuel為燃油消耗量，kg/h；Te為發(fā)動(dòng)機(jī)轉(zhuǎn)矩，N·m；ωe為發(fā)動(dòng)機(jī)轉(zhuǎn)速，r/min。

發(fā)動(dòng)機(jī)燃油消耗可根據(jù)當(dāng)前時(shí)刻發(fā)動(dòng)機(jī)的轉(zhuǎn)矩和轉(zhuǎn)速通過發(fā)動(dòng)機(jī)燃油消耗特性查表插值得出。

電機(jī)效率可根據(jù)電機(jī)效率特性查表插值獲得。

ηm=ηm(Tm,ωm)

(5)

式中：ηm為電機(jī)效率；Tm為電機(jī)轉(zhuǎn)矩，N·m；ωm為電機(jī)轉(zhuǎn)速，r/min。

電池的電壓、電流和效率都與溫度有關(guān)，因此電池的建模具有一定的復(fù)雜性。為了簡化模型方便計(jì)算，本文中忽略溫度對電池參數(shù)的影響，電池SOC數(shù)學(xué)模型為

SOC(k+1)=SOC(k)-

(6)

式中：Uoc為電池的開路電壓，V；Rint為電池的內(nèi)阻，Ω；Rt為電池的終端電阻，Ω；Qmax為電池的最大電量，C。

變速器換擋數(shù)學(xué)模型為

(7)

式中：gx(k)為當(dāng)前時(shí)刻擋位；gx(k+1)為下一時(shí)刻擋位；gshift(k)為換擋信號，1表示升擋，-1表示降擋，0表示維持原擋位。

2 控制策略

本文中的動(dòng)態(tài)規(guī)劃控制策略以燃油消耗為基本目標(biāo)函數(shù)，兼顧電池電量平衡和擋位的穩(wěn)定程度，對基本目標(biāo)函數(shù)進(jìn)行修正：

β(SOC(N+1)-SOC(f))2

(8)

式中：bfuel(k)為k時(shí)刻時(shí)這一階段的燃油消耗，kg；gx(k)和gx(k+1)分別為k時(shí)刻和k+1時(shí)刻的擋位；SOC(N+1)為電池SOC的終值；SOC(f)為電池初始值；α和β為權(quán)重因子。

狀態(tài)變量的增加會(huì)導(dǎo)致計(jì)算量成倍地增長，為減少計(jì)算量提高算法的實(shí)時(shí)性，應(yīng)盡量減少狀態(tài)變量的個(gè)數(shù)并且仍能夠反映出系統(tǒng)的特點(diǎn)。混合動(dòng)力汽車燃油消耗由兩部分組成：一部分是發(fā)動(dòng)機(jī)的燃油消耗；另一部分是消耗的電量折算出的燃油消耗。發(fā)動(dòng)機(jī)的燃油消耗可由式(4)求得；電量消耗可由式(6)求得。由于本文中所研究的混合動(dòng)力系統(tǒng)為并聯(lián)結(jié)構(gòu)，若車速和擋位一定，整車需求轉(zhuǎn)矩和發(fā)動(dòng)機(jī)與電機(jī)的轉(zhuǎn)速便可求得。因此與整車的燃油消耗有關(guān)的用來迭代計(jì)算的狀態(tài)變量精簡為車速和電池SOC，其狀態(tài)轉(zhuǎn)移方程如式(1)和式(6)所示。系統(tǒng)的控制量顯然是發(fā)動(dòng)機(jī)轉(zhuǎn)矩、電機(jī)轉(zhuǎn)矩和變速器擋位。

為保證混合動(dòng)力系統(tǒng)安全穩(wěn)定的工作，需要對系統(tǒng)的一些狀態(tài)量和控制量進(jìn)行如下約束：

(9)

動(dòng)態(tài)規(guī)劃算法的核心思想是以每階段代價(jià)函數(shù)之和(即式(8)目標(biāo)函數(shù))最小為目標(biāo)，確定一組最優(yōu)的控制序列。如式(10)和式(11)所示，其中x(k)為k時(shí)刻狀態(tài)變量，u(k)為k時(shí)刻控制變量，x(k+1)為k+1時(shí)刻狀態(tài)變量。也就是要計(jì)算出一組控制序列u(k),u(k+1),…,u(N)，使式(11)表示的代價(jià)函數(shù)值最小。

x(k+1)=f(x(k),u(k))

(10)

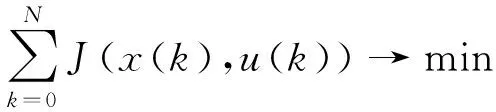
(11)

動(dòng)態(tài)規(guī)劃采用逆序迭代法，如果優(yōu)化過程有N+1個(gè)狀態(tài)，優(yōu)化過程可分為N個(gè)階段，則從第N階段開始迭代，即

Q(x,u,N-1)=J(x(N-1),u(N-1))+

V(f(x(N-1),u(N-1)),N)

(12)

V(f(x(N-1),u(N-1)),N)=0

(13)

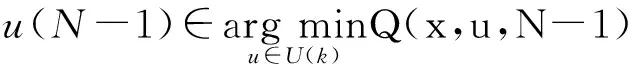
(14)

以此類推，第N-1階段：

Q(x,u,N-2)=J(x(N-2),u(N-2))+

V(f(x(N-2),u(N-2)),N-1)

(15)

V(f(x(N-2),u(N-2)),N-1)=Q(x,u,N-1)

(16)

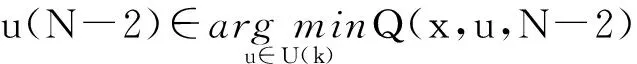
(17)

第k階段(即k-1時(shí)刻到k時(shí)刻)：

Q(x,u,k-1)=J(x(k-1),u(k-1))+

V(f(x(k-1),u(k-1)),k)

(18)

V(f(x(k-1),u(k-1)),k)=Q(x,u,k)

(19)

(20)

第1階段：

Q(x,u,0)=J(x(0),u(0))+

V(f(x(0),u(0)),1)

(21)

V(f(x(0),u(0)),1)=Q(x,u,1)

(22)

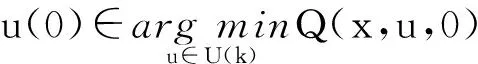
(23)

從而得出最優(yōu)控制序列：

u(0),u(1),…,u(N-1)

由于動(dòng)態(tài)規(guī)劃采用逆序迭代法，故須在確定的駕駛循環(huán)工況下進(jìn)行優(yōu)化計(jì)算。由于在駕駛循環(huán)工況中，車速隨時(shí)間而變化，也就是要預(yù)先知道優(yōu)化過程中每一時(shí)刻的車速。由于車輛在實(shí)際運(yùn)行的過程中，下一時(shí)刻的車速是未知的，因此動(dòng)態(tài)規(guī)劃只能用于離線優(yōu)化，并且優(yōu)化結(jié)果只適用于特定駕駛循環(huán)工況，不能實(shí)時(shí)應(yīng)用[11-14]。

下面將對傳統(tǒng)的動(dòng)態(tài)規(guī)劃進(jìn)行優(yōu)化。假設(shè)在未知駕駛循環(huán)工況的情況下，如果能求出車速的狀態(tài)轉(zhuǎn)移概率，便可預(yù)測出下一時(shí)刻不同車速出現(xiàn)的概率，那么系統(tǒng)狀態(tài)轉(zhuǎn)移的代價(jià)函數(shù)便可根據(jù)下一時(shí)刻車速出現(xiàn)的概率加權(quán)平均得到。也就是說實(shí)際迭代過程中每階段狀態(tài)轉(zhuǎn)移產(chǎn)生的代價(jià)并非兩個(gè)確定車速狀態(tài)轉(zhuǎn)移產(chǎn)生的燃油消耗，而是基于車速狀態(tài)轉(zhuǎn)移概率計(jì)算每種狀態(tài)轉(zhuǎn)移的燃油消耗的加權(quán)平均值。那么在進(jìn)行逆序迭代的時(shí)候就無須預(yù)先知道駕駛循環(huán)工況，即優(yōu)化過程中每一時(shí)刻的車速。因此動(dòng)態(tài)規(guī)劃的迭代方程可優(yōu)化為

Q(x(i),u(i),l)=J(x(i),u(i))+

(24)

x(j)=x(i+1)=f(x(i),u(i))

(25)

V(x(i),l+1)=minQ(x(i),u(i),l)

(26)

u(i)∈arg minQ(x(i),u(i),L)

(27)

式中：j為在狀態(tài)i下一時(shí)刻可能出現(xiàn)的狀態(tài)，j=1,2,…,m；Pij(x)為車速從狀態(tài)i到狀態(tài)j的一步轉(zhuǎn)移概率；δ為收斂因子，其作用是使迭代盡快收斂，0<δ<1；l為迭代次數(shù)，l=0,1,…,L。

其中狀態(tài)轉(zhuǎn)移概率Pij(x)是通過對我國公交客車慢速駕駛循環(huán)工況、公交客車快速駕駛循環(huán)工況、北京駕駛循環(huán)工況、上海駕駛循環(huán)工況和長春駕駛循環(huán)工況等典型駕駛循環(huán)工況進(jìn)行數(shù)理統(tǒng)計(jì)計(jì)算得到。在計(jì)算車速轉(zhuǎn)移概率的過程中用到的各種駕駛循環(huán)工況，是在混合動(dòng)力客車開發(fā)過程中，檢驗(yàn)整車性能時(shí)常用的駕駛循環(huán)工況，能夠代表我國公交客車在各種運(yùn)行條件下的運(yùn)行特點(diǎn)。因此對這些駕駛循環(huán)工況進(jìn)行數(shù)理統(tǒng)計(jì)得到的車速轉(zhuǎn)移概率可以反映出我國公交客車在運(yùn)行過程中車速的變化特點(diǎn)。Pij(x)的計(jì)算公式[15]為

(28)

式中：nij為車速從狀態(tài)i轉(zhuǎn)移到狀態(tài)j發(fā)生的次數(shù)；nitotal為車速從狀態(tài)i轉(zhuǎn)移到其他狀態(tài)次數(shù)的總和。

在計(jì)算車速轉(zhuǎn)移概率時(shí)，首先根據(jù)以上駕駛循環(huán)工況的車速覆蓋范圍選取[0,1,2,3,…,60km/h]為車速的狀態(tài)空間，初始車速為非整數(shù)值時(shí)，均圓整為整數(shù)車速。式(28)中的狀態(tài)i和狀態(tài)j為狀態(tài)空間里任意一個(gè)車速。根據(jù)式(28)便可得出車速從狀態(tài)i變化為狀態(tài)j的概率。通過計(jì)算車速狀態(tài)空間里所有車速的狀態(tài)轉(zhuǎn)移概率便可以得到車速的狀態(tài)轉(zhuǎn)移概率矩陣，如式(29)所示。在動(dòng)態(tài)規(guī)劃算法迭代的過程中，已知當(dāng)前時(shí)刻車速的狀態(tài)，便可鎖定狀態(tài)轉(zhuǎn)移概率矩陣中的一行。這一行中的每個(gè)元素便是由當(dāng)前時(shí)刻轉(zhuǎn)移到下一時(shí)刻各種車速狀態(tài)的概率。在動(dòng)態(tài)規(guī)劃算法實(shí)際迭代的過程中可以查表得到。

(29)

3 臺架試驗(yàn)

為驗(yàn)證優(yōu)化后控制策略的在線實(shí)時(shí)控制效果，進(jìn)行了臺架試驗(yàn)。試驗(yàn)臺架的整體構(gòu)型和動(dòng)力總成參數(shù)與混合動(dòng)力原型客車基本一致，如圖2所示，臺架整體布局如圖3所示。

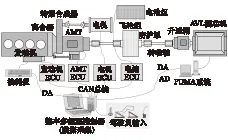
圖2 混合動(dòng)力客車臺架構(gòu)型示意圖

圖3 混合動(dòng)力客車臺架

圖4 行駛阻力模擬裝置

為模擬車輛實(shí)際運(yùn)行過程中的行駛阻力，試驗(yàn)臺架除了有與實(shí)車相同的動(dòng)力總成外，還有行駛阻力模擬裝置，如圖4所示。用AVL公司的底盤測功機(jī)模擬行駛阻力，轉(zhuǎn)速范圍0-3 500r/min，恒定功率為220kW，峰值功率270kW，可進(jìn)行數(shù)據(jù)采集、處理和分析。以北京動(dòng)態(tài)循環(huán)工況為目標(biāo)循環(huán)工況。北京動(dòng)態(tài)循環(huán)工況與傳統(tǒng)的北京循環(huán)工況相比，其動(dòng)態(tài)特性更明顯，是在對大量的公交客車運(yùn)行數(shù)據(jù)統(tǒng)計(jì)的基礎(chǔ)上得到的，既可以作為汽車動(dòng)力裝置選型和設(shè)計(jì)的基礎(chǔ)，又是汽車經(jīng)濟(jì)性、動(dòng)力性和排放性能檢驗(yàn)的標(biāo)準(zhǔn)工況。北京動(dòng)態(tài)工況歷時(shí)1 925s，行程7.24km，經(jīng)歷20個(gè)加減速的過程，最高車速46.7km/h，可以反映出北京客車運(yùn)行的特點(diǎn)和動(dòng)態(tài)特性。圖5為北京動(dòng)態(tài)循環(huán)工況循環(huán)車速時(shí)間歷程曲線。

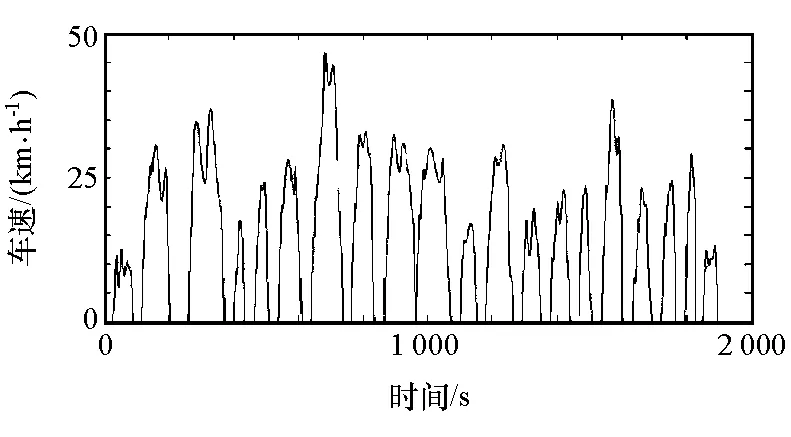
圖5 北京動(dòng)態(tài)循環(huán)工況

在試驗(yàn)中由駕駛員跟隨目標(biāo)循環(huán)工況，檢驗(yàn)基于狀態(tài)轉(zhuǎn)移概率的動(dòng)態(tài)規(guī)劃控制策略的控制效果。要說明的是目標(biāo)循環(huán)工況只作為當(dāng)前時(shí)刻系統(tǒng)狀態(tài)的輸入量。在當(dāng)前時(shí)刻動(dòng)態(tài)規(guī)劃運(yùn)算的過程中，之后時(shí)刻的系統(tǒng)狀態(tài)是未知的，保證臺架試驗(yàn)是實(shí)時(shí)進(jìn)行的。在改進(jìn)后動(dòng)態(tài)規(guī)劃控制策略的控制下，試驗(yàn)臺架實(shí)際車速可以跟蹤目標(biāo)循環(huán)工況，并且換擋平穩(wěn)，如圖6所示。圖7和圖8為發(fā)動(dòng)機(jī)和電機(jī)的工作情況，可見改進(jìn)后的控制策略可以根據(jù)目標(biāo)循環(huán)工況的需求在線對發(fā)動(dòng)機(jī)和電機(jī)的轉(zhuǎn)矩進(jìn)行合理分配。圖9為電池的工作情況，可見電池SOC變化較平穩(wěn)。

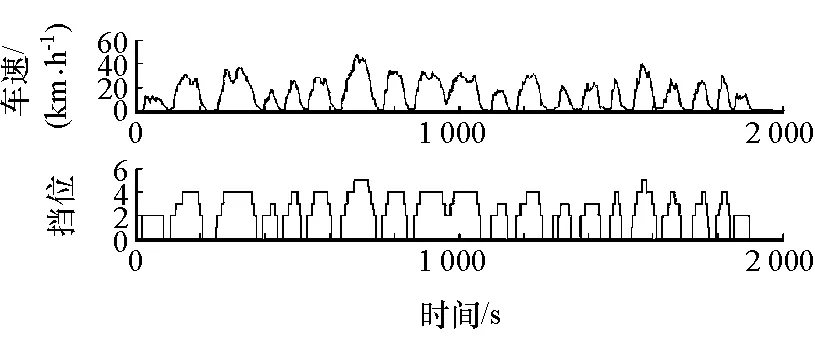
圖6 實(shí)際車速與擋位

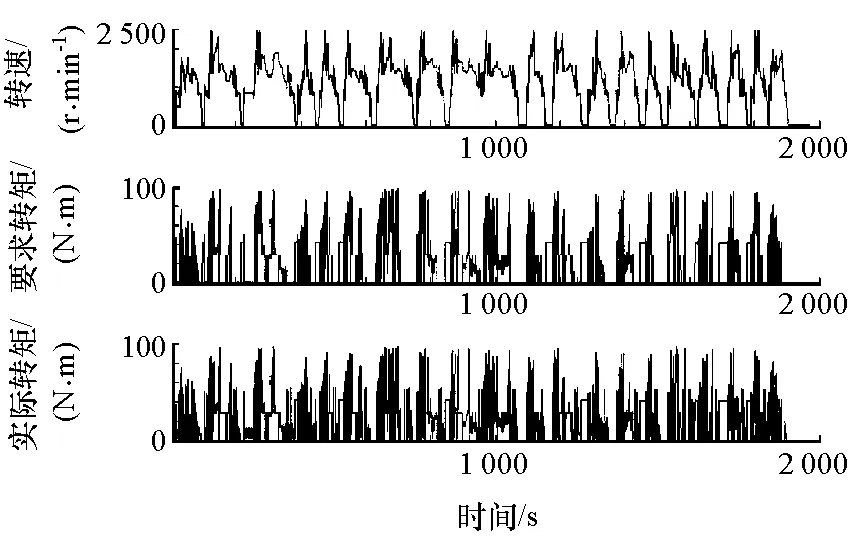
圖7 發(fā)動(dòng)機(jī)工作情況

圖8 電機(jī)工作情況

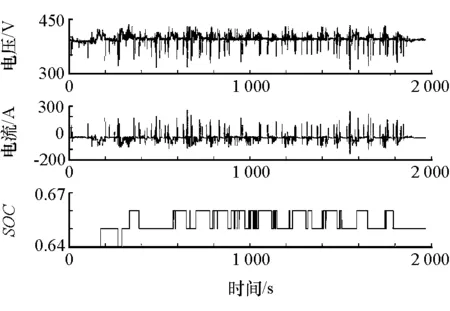
圖9 電池工作情況

為進(jìn)一步檢驗(yàn)控制策略控制效果，對發(fā)動(dòng)機(jī)的工作點(diǎn)進(jìn)行了對比分析。圖10為混合動(dòng)力原型車采用的邏輯門限值控制策略的發(fā)動(dòng)機(jī)工作點(diǎn)，圖11為基于狀態(tài)轉(zhuǎn)移概率的動(dòng)態(tài)規(guī)劃控制策略的發(fā)動(dòng)機(jī)工作點(diǎn)。圖中虛線為發(fā)動(dòng)機(jī)最優(yōu)工作線，可以看到落到發(fā)動(dòng)機(jī)最優(yōu)工作線附近的工作點(diǎn)更多，說明基于狀態(tài)轉(zhuǎn)移概率的動(dòng)態(tài)規(guī)劃控制策略對發(fā)動(dòng)機(jī)工作點(diǎn)的控制效果更好。

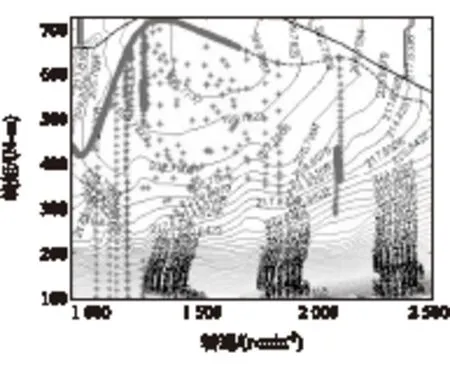
圖10 邏輯門限值控制策略發(fā)動(dòng)機(jī)工作點(diǎn)

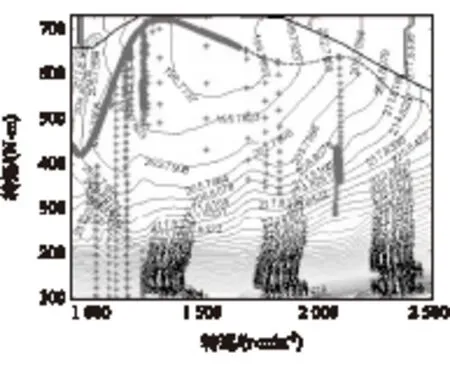
圖11 改進(jìn)后控制策略發(fā)動(dòng)機(jī)工作點(diǎn)

表2為落入發(fā)動(dòng)機(jī)高效率區(qū)域的工作點(diǎn)的統(tǒng)計(jì)結(jié)果。由表可見，原型客車采用的控制策略只有30.60%的工作點(diǎn)落入高效率區(qū)，而基于狀態(tài)轉(zhuǎn)移概率的動(dòng)態(tài)規(guī)劃控制策略控制下的發(fā)動(dòng)機(jī)有45.26%的工作點(diǎn)落入高效率區(qū)，提高了14.66個(gè)百分點(diǎn)。

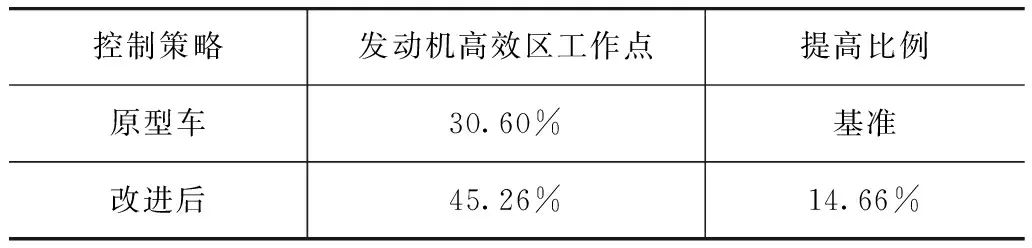
表2 發(fā)動(dòng)機(jī)高效區(qū)工作點(diǎn)對比

臺架試驗(yàn)采用量程為60kg電子秤稱量油箱質(zhì)量的方法，以試驗(yàn)開始前和試驗(yàn)結(jié)束后兩次讀數(shù)的差值作為整個(gè)試驗(yàn)消耗掉的燃油量，并根據(jù)標(biāo)準(zhǔn)GB/T 19754—2005中規(guī)定的電量消耗量和燃油消耗量的換算關(guān)系，計(jì)算出等效油耗。不同控制策略燃油經(jīng)濟(jì)性對比結(jié)果如表3所示。由表可見，基于狀態(tài)轉(zhuǎn)移概率的動(dòng)態(tài)規(guī)劃控制策略控制的百公里等效油耗比原型客車降低了18.88%。

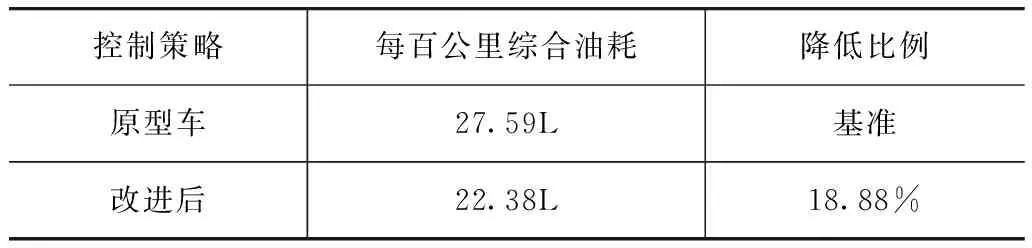
表3 等效油耗對比

4 結(jié)論

(1) 基于狀態(tài)轉(zhuǎn)移概率的混合動(dòng)力客車動(dòng)態(tài)規(guī)劃控制策略在進(jìn)行動(dòng)態(tài)規(guī)劃迭代的過程中可預(yù)測出下一時(shí)刻不同車速出現(xiàn)的概率，并且基于車速狀態(tài)轉(zhuǎn)移概率計(jì)算每種狀態(tài)轉(zhuǎn)移的燃油消耗的加權(quán)平均值。因此改進(jìn)后的動(dòng)態(tài)規(guī)劃控制策略在進(jìn)行優(yōu)化計(jì)算的過程中無需提前知道駕駛循環(huán)工況，為動(dòng)態(tài)規(guī)劃在混合動(dòng)力汽車整車控制中的在線實(shí)時(shí)應(yīng)用提供了理論支撐。

(2) 臺架試驗(yàn)證明：基于狀態(tài)轉(zhuǎn)移概率的混合動(dòng)力客車動(dòng)態(tài)規(guī)劃控制策略可以在線對混合動(dòng)力系統(tǒng)進(jìn)行實(shí)時(shí)控制；能夠根據(jù)目標(biāo)循環(huán)工況的需求在線對發(fā)動(dòng)機(jī)和電機(jī)的轉(zhuǎn)矩進(jìn)行合理分配，換擋平穩(wěn)，電池SOC在預(yù)定的區(qū)域內(nèi)基本保持平衡；相比原型混合動(dòng)力客車，本控制策略可以進(jìn)一步優(yōu)化發(fā)動(dòng)機(jī)工作點(diǎn)，提高整車燃油經(jīng)濟(jì)性。

[1] 朱道偉,謝輝,嚴(yán)英,等.基于道路工況自學(xué)習(xí)的混合動(dòng)力城市客車控制策略動(dòng)態(tài)優(yōu)化[J].機(jī)械工程學(xué)報(bào),2010,46(6):33-38.

[2] 舒紅,劉文杰,袁景敏,等.混聯(lián)型混合動(dòng)力汽車能量管理策略優(yōu)化[J].農(nóng)業(yè)機(jī)械學(xué)報(bào),2009,40(3):31-35.

[3] 鄒淵,侯仕杰,韓爾樑,等.基于動(dòng)態(tài)規(guī)劃的混合動(dòng)力商用車能量管理策略優(yōu)化[J].汽車工程,2012,34(8):663-668.

[4] 浦金歡,殷承良,張建武.并聯(lián)型混合動(dòng)力汽車燃油經(jīng)濟(jì)性最優(yōu)控制[J].上海交通大學(xué)學(xué)報(bào),2006,40(6):947-951.

[5] 隗寒冰,秦大同,段志輝,等.重度混合動(dòng)力汽車燃油經(jīng)濟(jì)性和排放多目標(biāo)優(yōu)化[J].汽車工程,2011,33(11):937-941.

[6] SERRAO L, ONORI S, RIZZONI G. A Comparative Analysis of Energy Management Strategies for Hybrid Electric Vehicles[J]. Journal of Dynamic Systems, Measurement, and Control,2011,133(3):1-9.

[7] MURPHEY Y L, PARK J, CHEN Z H, et al. Intelligent Hybrid Vehicle Power Control-Part I: Machine Learning of Optimal Vehicle Power[J]. IEEE Transactions on Vehicular Technology,2012,61(8):3519-3530.

[8] BIANCHI D, ROLANDO L, SERRAO L, et al. A Rule-based Strategy for a Series/Parallel Hybrid Electric Vehicle: An Approach Based on Dynamic Programming[C]. ASME 2010 Dynamic Systems and Control Conference, Cambridge, Massachusetts, USA, September 12-15,2010:507-514.

[9] KUM D, PENG H, BUCKNOR N K. Supervisory Control of Parallel Hybrid Electric Vehicles for Fuel and Emission Reduction[J]. Journal of Dynamic Systems, Measurement, and Control,2011,133(6):1-10.

[10] ZHANG C, VAHIDI A, PISU P, et al. Role of Terrain Preview in Energy Management of Hybrid Electric Vehicles[J]. IEEE Transactions on Vehicular Technology,2010,59(3):1139-1147.

[11] KIM N, CHA S, PENG H. Optimal Control of Hybrid Electric Vehicles Based on Pontryagin’s Minimum Principle[J]. IEEE Transactions on Control Systems Technology,2011,19(5):1279-1287.

[12] ZHANG C, VAHIDI A. Route Preview in Energy Management of Plug-in Hybrid Vehicles[J]. IEEE Transactions on Control Systems Technology,2012,20(2):546-553.

[13] KUTTER S, BAKER B. An Iterative Algorithm for the Global Optimal Predictive Control of Hybrid Electric Vehicles[C]. IEEE Vehicle Power and Propulsion Conference (VPPC), Chicago, IL, United States, September 6-9,2011:6043004,1-6.

[14] GENG B, MILLS J K, SUN D. Predictive Control for Plug-in Microturbine Powered Hybrid Electric Vehicles Using Telemetry Information[C]. IEEE International Conference on Robotics and Biomimetics, Phuket, Thailand, December 7-11,2011:1468-1473.

[15] DAI J. Isolated Word Recognition Using Markov Chain Models[J]. IEEE Transactions on Speech & Audio Processing,1995,3(6):458-463.

Control Strategy for Hybrid Electric Bus Based on State Transition Probability

Tang Xianzhi, Wang Bo, Yang Shujun, Di Liming & Xia Huaicheng

CollegeofVehiclesandEnergy,YanshanUniversity,Qinhuangdao066004

A mathematical model for hybrid electric bus and the objective function, state transition equations and iterative equations of dynamic programming (DP) are established and an improved DP control strategy for hybrid electric bus based on state transition probability is proposed. Driving cycle is predicted based on state transition probability, to make the fuel consumption by state transition in the process of DP iteration be the weighted mean based on the state transition probability of vehicle speed. The improved control strategy can be used for real time online control without given driving cycle, enhancing the real time application capability of DP. The results of bench test indicate that the improved control strategy can reasonably assign the required torques between engine and electric motor online, resulting in a balance of battery SOC, a smooth gear shift with the working points of engine optimized and the fuel economy of vehicle improved.

HEV; state transition probability; dynamic programming; control strategy

*國家自然科學(xué)基金青年基金(51505414)、國家自然科學(xué)基金(51175449)、河北省高等學(xué)校科學(xué)研究項(xiàng)目(Z2015081)、國家自然科學(xué)基金青年基金(51406174)和燕山大學(xué)博士基金項(xiàng)目(B794)資助。

原稿收到日期為2014年9月28日，修改稿收到日期為2014年12月28日。