兩方程模型計算轎車氣動性能的適用性研究*

朱 暉,楊志剛

(同濟大學,上海地面交通工具風洞中心,上海 201804)

2016202

兩方程模型計算轎車氣動性能的適用性研究*

朱 暉,楊志剛

(同濟大學,上海地面交通工具風洞中心,上海 201804)

采用兩方程湍流模型進行穩態數值仿真被廣泛應用于與汽車空氣動力學相關的工程實踐及科學研究中。基于統一的硬件平臺和相關的參數設置，采用Realizablek-ε模型、k-ωSST模型和4種低雷諾數模型對某一車身全尺寸模型外部繞流場進行數值計算。以同一模型的風洞試驗數據為準，通過計算獲得氣動升/阻力、車身表面壓力和尾跡區流場結構等相關信息，對比研究了不同兩方程模型對汽車外流場的計算能力。

轎車；氣動性能；兩方程模型；穩態數值仿真

前言

汽車空氣動力學與車身結構和造型風格直接相關，從而影響燃油經濟性、操控穩定性和視覺美感，成為科學研究及產品研發過程中的核心內容之一。

目前，計算流體力學方法被廣泛應用于汽車空氣動力學特性研究中，該方法中湍流模型構建或選擇恰當與否直接影響對汽車外部繞流場解算的準確性和實時性[1-3]。

汽車外流場包含附著、邊界層轉捩、局部分離、尾跡大分離流動現象，屬于復雜的高雷諾數臨地面鈍體繞流范疇。基于流動現象特征和穩態分析前提，由于對分離和旋轉等強三維流動具有較高的仿真精度，在兩方程框架中Realizablek-ε模型及k-ωSST模型常被引入針對汽車外流場的數值分析中[4-7]。

低雷諾數模型亦屬于兩方程模型，此類模型避開壁面函數概念，對高雷諾數湍流模型方程中的經驗常數或函數進行近壁衰減和分子黏性效應修正，在學理層面和低雷諾數或簡單三維流動模擬實踐中體現出優勢[8-11]，但對高雷諾數轎車繞流場計算的適用性尚需進一步研究。

本文中以自主研發的低阻車型為對象，在風洞實測數據的基礎上，研究在穩態分析前提下兩方程湍流模型在車體不同部位存在不同運動特征流動的仿真特性，并結合車體所受氣動升/阻力的計算和試驗數據的比較，明確兩方程湍流模型在高雷諾數轎車繞流場數值仿真中的特點與適用性。

1 兩方程湍流模型

Realizablek-ε湍流模型引入部分雷諾應力數學約束，湍動能k及耗散率ε基本方程[12]為

(1)

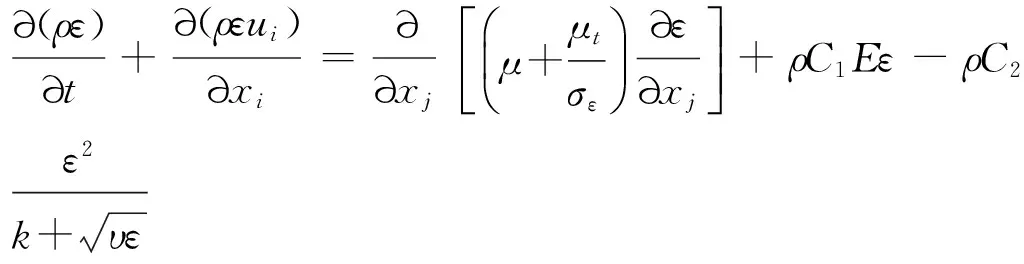
(2)

式中：Gk為由平均速度梯度引起的湍動能k產生項；σk和σε分別為與湍動能k和耗散率ε對應的Prandtl數。

k-ωSST模型湍流模型的湍動能k和ω基本方程[13]為

(3)

(4)

(5)

(6)

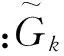
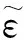
(7)

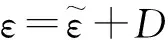
(8)

(9)

(10)

不同的低雷諾數模型對相關參數的模化方式和常數的取值不盡相同。

LS(Launder-Sharma)模型模化方式[14]為

fμ=exp[-3.4/(1+ReT/50)2]

(11)

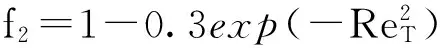
(12)

LB(Lam-Bremhorst)模型模化方式[15]為

fμ=[1-exp(-0.0165Rey)]2(1+20.5/ReT)

(13)

f1=1+(0.05/fμ)3

(14)

(15)

YS(Yang-Shih)模型模化方式[16]為

(16)

(17)

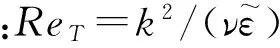
2 流場仿真相關信息

試驗和數值仿真對象統一為自主設計的某款車型的全尺寸模型，其造型特點為：車體A柱與車頭實行一體式設計；車體頂部和C柱實行一體式設計并延伸至車尾；車體側面采用半分體式設計；尾部采用簡潔的“截尾”設計；車型底部光滑；有后視鏡。

模型長L=4622mm，寬W=1783mm、高H=1460mm，軸距為2590mm，輪距為1600mm，正投影面積為2.273m2；輪胎采用帶輻條的仿真輪胎，具體構造如圖1所示。

圖1 模型構造

采用尺度從1～10mm不等的三角形網格對模型表面進行細化劃分，其原因為：(1)車身底部與地面之間間隙狹小，可能導致體網格生成困難或者質量不高，從而加細網格；(2)在型面結合部位流動極易產生扭曲變形，需要細化網格以更好地捕捉流場信息；(3)為保證與試驗狀態完全一致，保留了仿真模型的全部細節(車輪輻條、螺栓、車軸法蘭等)，因此細化面網格。

仿真空間區域，長為模型長的10倍，寬為模型寬的10倍，高為模型高的5倍，阻塞比為1.75%；X軸正向為空氣流動方向(圖中為從左到右),Z軸正向垂直向上，Y軸正向以右手定則確定，如圖2所示。

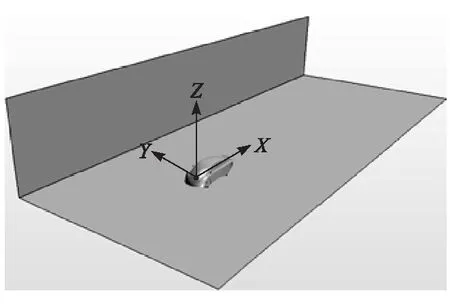
圖2 計算區域

為減輕數值黏性的影響，大部分計算區域劃分為大小不等的六面體網格。為高效利用計算資源并提高計算精度，在包裹模型和流場變化劇烈的局部區域采用統一尺度對體網格進行加密。近壁面第一層網格中心離壁面的法向高度，Realizablek-ε模型和k-ωSST模型以y+(y*)=30～300加以控制，低雷諾數模型以y+<10加以控制。在實現邊界層網格全面覆蓋模型和相關型面細節的條件下，體網格質量控制標準為skewness<0.94。Realizablek-ε模型和k-ωSST模型的總網格數接近2 200萬，低雷諾數模型的總網格數接近3 500萬，具體布局見圖3。

圖3 體網格布局

參照試驗風洞的結構、氣流品質和運行工況，入口處統一采用速度入口邊界條件(velocity inlet)，認為速度均勻分布，U=30m/s，V=W=0；入口湍流強度為1%，湍流黏性比為10；出口采用壓力出口邊界條件，表壓取為0，出口湍流強度和湍流黏性比的確定與進口類似。按車長計算的雷諾數為Re≈9.38×106。

地面和車身(含車輪)皆采用無滑移邊界條件；風洞具備五帶移動系統，為與試驗情況保持一致，車輪采用MRF法模擬轉動，地面采用移動壁面邊界；計算域左右兩側和頂部采用對稱邊界條件。

3 計算結果

風洞試驗在同濟大學地面交通工具風洞中心空氣動力學整車風洞中完成，如圖4所示。

圖4 試驗現場

計算過程中，在監測殘差的基礎上，對車身的阻力系數CD和升力系數CL進行監測。計算結束后統計出的相關數據見表1，表1中相對誤差Err計算以風洞試驗值為準，皆取絕對值。

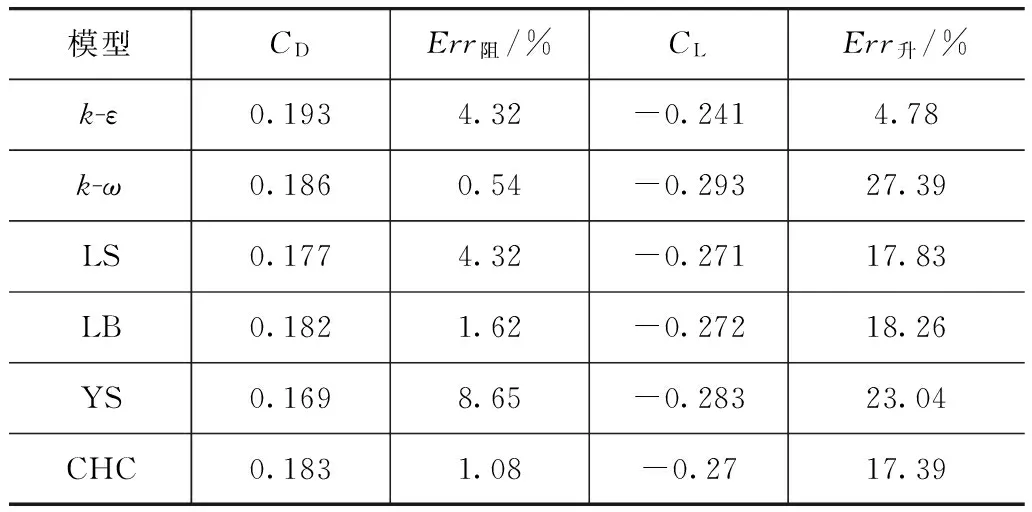
表1 CD及CL比較

由表1可見：k-ωSST模型對氣動阻力的計算準確度最高，CHC和LB模型次之，Realizablek-ε湍流模型和LS模型再次之，相對誤差皆小于5%；Realizablek-ε湍流模型對氣動升力的計算準確度最高，CHC和LS模型次之，LB模型再次之，但只有Realizablek-ε湍流模型計算結果的相對誤差小于5%，其他模型計算結果的相對誤差皆大于15%。

車身表面布置256個測壓點，如圖5所示。壓力數據的采集由電子壓力掃描閥系統(256通道)完成；測壓系統由電子掃描壓力傳感器模塊、測壓點選通接口板、A/D變換板、電子掃描靜態測壓系統的壓力控制單元、數據采集控制單元和微機組成；壓力掃描閥采樣頻率取5Hz，每個樣本點采集300個采樣點，為減少偶然誤差，提高模型表面壓力測量結果的精度和可信性，每個測點采集2個樣本進行數據平均。

圖5 表面測壓點分布

圖6示出車體前部及頂部縱向對稱截面處各測壓點的平均壓力系數。由圖可見：由于前窗及車頂連接處造型特征的連貫性，氣流流經該處時未形成“死水區”，且氣流在車身上部未出現流動不穩定現象，所以6種湍流模型計算結果與試驗值皆符合較好。

圖6 縱向對稱面壓力系數

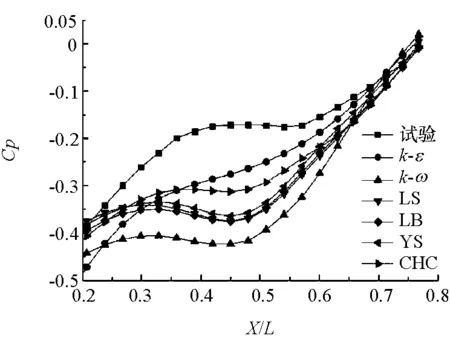
圖7 底部截面壓力系數

圖7示出車體底部縱向對稱截面處測壓點的平均壓力系數。由圖可見，各種模型預測的平均壓力系數(尤其在X/L=0.3～0.6范圍)與試驗結果差別很大。

圖8為車體側面選定測壓點(Z/H=0.145～0.433)的平均壓力系數。由圖可見，各種模型預測的平均壓力系數與試驗值都比較接近，尤其是X/L>3以后吻合很好。

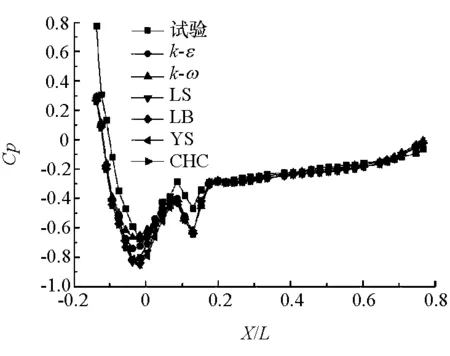
圖8 車體側面壓力系數

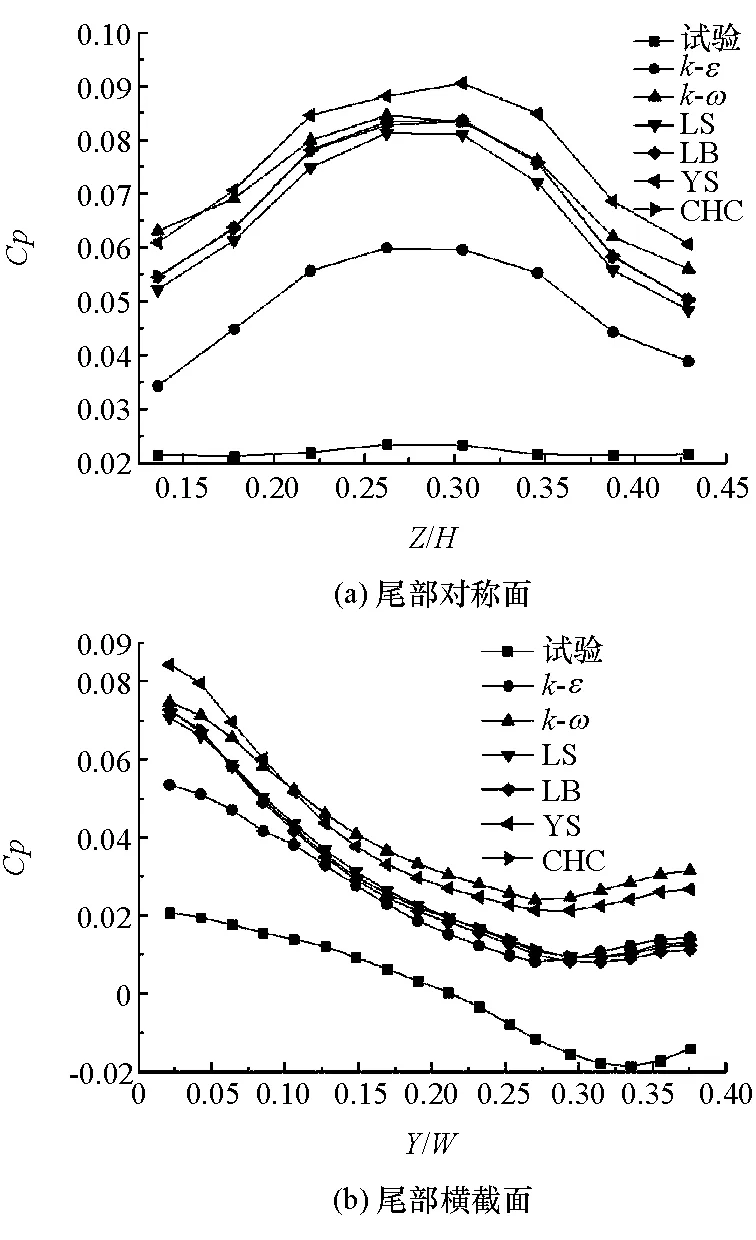
圖9 尾部截面壓力系數

圖9為車體尾部測壓點的平均壓力系數。由圖可見，由于車體尾部大分離結構的存在，使6種湍流模型計算結果在數值上與試驗值皆存在較大偏差，但趨勢基本一致。對于尾部縱向對稱面測點(圖9(a))，Realizablek-ε湍流模型明顯優于其他模型，其次是LS和LB模型與CHC模型，YS模型的計算值與試驗值相差最大；而對于尾部橫向截面測點(圖9(b))，Realizablek-ε，LS，LB和CHC模型預測能力相當，k-ωSST模型的計算值與試驗值相差最大。總之，在針對車體尾流區大分離結構的計算實踐中Realizablek-ε模型計算能力最強，LS，LB和CHC模型能力相當，k-ωSST和YS模型較差。

流線圖形式具有清晰直觀的特點，有利于對流場結構進行比較，圖10示出縱截面處6種湍流模型算得的車體尾跡區流場尾渦的特征。

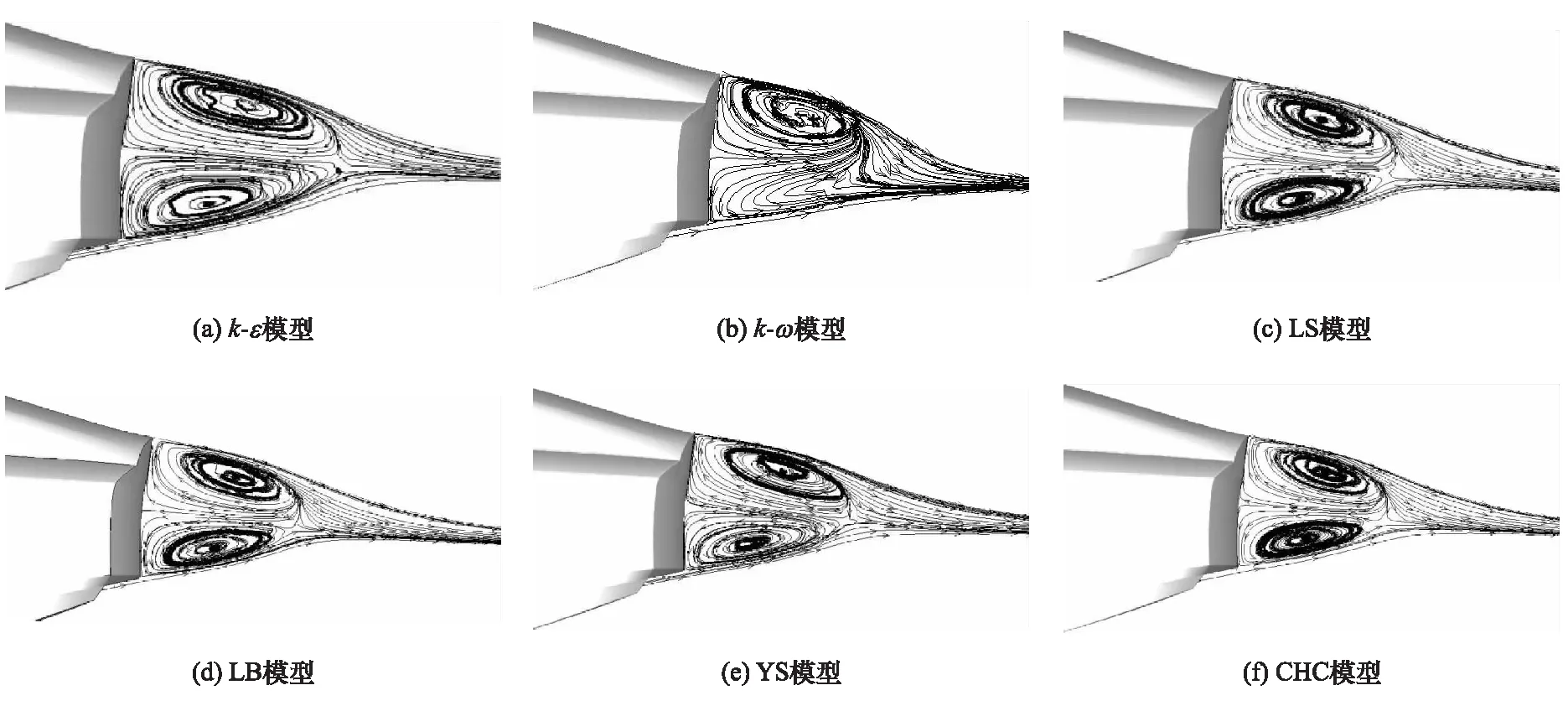
圖10 截面尾渦

由圖10可見：除k-ωSST模型外，其他5種湍流模型皆計算出尾跡區存在對渦的現象，且對渦尺度基本一致。綜合圖9與圖10所示數據可知：YS模型對車尾剪切流動特征預測過度。在整車風洞中使用PIV等流場精確顯示技術尚存在困難，因此本次風洞試驗未獲取流場信息，但由圖10可知，在針對尾跡區臨地面流動的計算中，有兩種可能：(1)k-ωSST模型預測不足；(2)其他兩方程模型預測過度。

4 結論

基于相同網格結構、同類型湍流模型相同量級的網格數量、相同的仿真設置、統一的硬件配置；以試驗數據為準，通過對比分析升/阻力系數、表面壓力和尾跡區流場結構，總結數值仿真中兩方程湍流模型穩態計算能力如下：

(1) 對流動三維性弱及未出現分離的車體頭部，分離點明確的車體頂部區域流動，6種湍流模型預測能力相當，且與試驗值符合良好；

(2) 對車體底部存在地面效應的流動，CHC模型預測能力最強，Realizablek-ε模型存在趨勢失真現象；

(3) 對車體側部三維性強且分離點不穩定區域流動，6種湍流模型預測能力相當，與試驗值相比趨勢一致性良好；

(4) 對車體尾部分離點明確但存在大分離結構流動，6種湍流模型計算值與試驗值相比趨勢一致性良好，Realizablek-ε模型計算能力最強，YS模型存在剪切流動特征預測過度現象；

(5) 結合CD和CL比較數據，Realizablek-ε模型對高雷諾數臨地面鈍體繞流場的預測能力強，但針對車體底部的計算結果可能存在趨勢失真現象，CHC模型對高雷諾數臨地面鈍體繞流場的預測能力最均衡，但額外多出1 200萬單位網格對應的計算量。

[1] HUCHO W H. Aerodynamics of road vehicles[M]. 4nd ed. SAE Inc,2004.

[2] 谷正氣.汽車空氣動力學[M].北京:人民交通出版社,2005.

[3] 傅立敏.汽車空氣動力學[M].北京:機械工業出版社,1998.

[4] 王夫亮,傅立敏.側風對轎車氣動特性影響的數值模擬研究[J].哈爾濱工業大學學報,2006(8):1255-1258.

[5] 龔旭,谷正氣,李振磊,等.側風狀態下轎車氣動特性數值模擬方法的研究[J].汽車工程,2010,32(1):13-16.

[6] 張英朝.汽車空氣動力學數值模擬技術[M].北京:北京大學出版社,2011.

[7] 谷正氣,姜波,何憶斌,等.基于SST湍流模型的超車時汽車外流場變化的仿真分析[J].汽車工程,2007,29(6):494-496.

[8] HRENYA C M, BOLIO E J, CHAKRABARTI D, et al. Comparison of low Reynolds numberk-εturbulence models in predicting fully developed pipe flow[J]. Chemical Engineering Science,1995,50(12):1923-1941.

[9] GANESH R I, SAVASH Y. Comparison of low Reynolds numberk-εmodels in simulation of momentum and heat transport under high free stream turbulence[J]. International Journal of Heat and Mass Transfer,1999,42:723-737.

[10] SUSHIL K R, MANAB K D. Comparison of two low Reynolds number turbulence models for fluid flow study of wall bounded jets[J]. International Journal of Heat and Mass Transfer,2013,61:365-380.

[11] CARLA C, RUI S, FERNANDO G, et al. Application of different low Reynoldsk-εturbulence models to model the flow of concentrated pulp suspensions in pipes[J]. Procedia Engineering,2015,102:1326-1335.

[12] SHIH T H, LIOU W W, SHABBIR A, et al. A newk-εeddy viscosity model for high Reynolds number turbulent flows-model development and validation[J]. Computer and Fluids,1995,24(3):227-238.

[13] MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal,1994,32(8):1598-1605.

[14] LAUNDER B E, SHARMA B I. Application of the energy dissipation model of turbulence to the calculation of flow near a spinning disc[J]. Letters in Heat and Mass Transfer,1974,1:131-139.

[15] LAM C K G, BREMHORST K. A modified form of thek-εmodel for predicting wall turbulence[J]. Journal of Fluids Engineering,1981,103(3):456-460.

[16] YANG Z, SHIH T H. New time scale basedk-εmodel for near-wall turbulence[J]. AIAA Journal,1993,31(7):1191-1198.

[17] JONES W P, LAUNDER B E. The calculation of low Reynolds number phenomena with a two-equation model of turbulence[J]. International Journal of Heat and Mass Transfer,1973,16:1119-1130.

[18] CHANG K C, HSIEH W D, CHEN C S. A modified low Reynolds number turbulence model applicable to recirculating flow in pipe expansion[J]. Journal of Fluids Engineering,1995,117:417-423.

[19] HSIEH W D, CHANG K C. Calculation of wall heat transfer in pipe-expansion turbulence flows[J]. International Journal of Heat and Mass Transfer,1996,39:3813-3822.

A Study on the Applicability of Two-equation Models to theCalculation of Aerodynamic Performance of Sedan

Zhu Hui & Yang Zhigang

TongjiUniversity,ShanghaiAutomotiveWindTunnelCenter,Shanghai201804

The steady-state numerical simulations with two-equation turbulence models are widely used in engineering practice and scientific research related to vehicle aerodynamics. Based on the same hardware platform and related parameters setting, Realizablek-εmodel,k-ωSST model and four low Reynolds number models are adopted to conduct numerical calculation on the flow field around a full scaled vehicle body model. According to the related information on aerodynamic lift and drag, the surface pressure on vehicle body and the wake structure of flow field, with the wind tunnel test data of the same model as reference base, the calculation abilities of different two-equation models regarding vehicle exterior flow filed are comparatively studied.

car; aerodynamic performance; two-equation model; steady-state numerical simulation

*上海市地面交通工具風洞專業技術服務平臺(16DZ2290400)資助。

原稿收到日期為2015年10月13日，修改稿收到日期為2015年12月14日。