地鐵車輛牽引逆變器熱管散熱器的溫升試驗及熱仿真

丁　杰，張　平

(1.湘潭大學 土木工程與力學學院，湖南 湘潭　411105；2.南車株洲電力機車研究所有限公司 南車電氣技術與材料工程研究院，湖南 株洲　412001)

牽引逆變器是地鐵車輛的關鍵部件，而絕緣柵雙極型晶體管(Insulated Gate Bipolar Transistor，IGBT)模塊是牽引逆變器中最為核心的器件。根據IGBT模塊的失效機理可知，其在封裝時各層材料的熱膨脹系數不一致，在長期高溫熱循環作用下可發生鋁鍵合線斷裂或脫落、硅芯片與襯板之間及襯板與基板之間的焊料層老化、柵極氧化層損壞和芯片失效等[1-3]。因此，IGBT模塊的散熱設計至關重要。

設計地鐵車輛牽引逆變器時，大多數采用熱管散熱器加走行風冷的方式，這樣可以省去風道和風機，簡化牽引逆變器的柜體結構，減少風機故障隱患和振動噪聲的影響[4-5]。但由于地鐵線路站點多、站間距短，列車啟停、加減速頻繁，使牽引逆變器的電氣參數不斷變化，導致IGBT模塊的損耗也實時改變；加之走行風速有快有慢，使熱管散熱器的散熱能力也相應變化，因此僅計算熱管散熱器和IGBT模塊某一工況的穩態溫升是無法準確評估熱管散熱器的性能和IGBT模塊的疲勞壽命的，有必要對其瞬態溫升進行計算。

目前，研究熱管散熱器和IGBT模塊溫升的方法可分為試驗分析法[6]和仿真分析法[7]。試驗分析法可在實驗室或實際運行的車輛中進行，優點是測試的溫升數據可信度高，缺點在于無法直接測量封裝于絕緣材料中芯片及焊料等部位的溫度。仿真分析法大多基于電氣、熱等學科建立仿真模型并進行單獨計算。電氣仿真借助Matlab/Simulink，Saber和Simplorer等軟件建立主電路仿真模型，得到IGBT模塊的電壓、電流等信息，進而計算芯片損耗。熱仿真主要有熱阻抗網絡、有限元、有限體積和模型降階等方法。熱阻抗網絡法將三維結構的導熱物體映射成為熱阻和熱容串級連接的一維熱阻抗網絡模型，使用方便、計算量很小，然而結溫、殼溫和熱管散熱器溫度是虛擬的理論平均值，與實際三維結構不同部位表現出明顯的溫度梯度有較大差異，且難以考慮同一熱管散熱器上不同IGBT模塊之間以及同一IGBT模塊中不同芯片之間的熱耦合效應[7]。有限元法需要將IGBT模塊和熱管散熱器的幾何結構劃分為有限元網格，在熱管散熱器與冷卻介質的接觸面設置等效對流換熱系數，而且計算時用較小的時間步長才能得到較為準確的瞬態溫度場計算結果，因此對計算機資源要求較高且求解速度慢。有限體積法是計算流體動力學(Computational Fluid Dynamic，CFD)中應用最為廣泛的方法，需要將IGBT模塊、熱管散熱器和冷卻介質劃分為有限體積網格，自動計算流固耦合面的對流換熱系數，其計算結果比有限元法更符合實際情況，然而邊界層對流動與換熱的影響使得網格尺寸被限制為較小的值，導致網格數量大幅度增加至數千萬，與此同時，流體區域的壓力與速度耦合，需要消耗大量的計算機資源進行迭代，才能得到收斂的穩態計算結果；并且，計算瞬態問題時，每一時間子步的迭代計算需要消耗計算機資源且計算結果文件需要數GB的硬盤存儲空間，因此，瞬態CFD計算的代價遠遠超出有限元法，極少應用于實際工程中的復雜對象。模型降階法[8-11]采用Krylov子空間、平衡截斷、正交分解、積分全等變換等算法得到階次較低的近似模型，可以在較高準確性基礎上極大提高計算效率。Simplorer和Caspoc等部分商業軟件包含了模型降階的功能，可以實現多個軟件的聯合仿真，由于商業軟件為了保證計算效率，輸出結果是多個探測點的變量變化曲線，很難輸出和云圖顯示整個物理場的數據，因此不能完全滿足實際的應用需求。

為快速、準確地分析地鐵車輛牽引逆變器熱管散熱器的性能及其IGBT模塊的溫升，本文首先搭建單個變流模塊的溫升試驗裝置，通過試驗得到可用于熱管散熱器熱仿真計算的輸入條件及驗證仿真結果準確性的試驗數據；然后采用FLUENT軟件對熱管散熱器進行穩態CFD仿真，得到其溫度場和對流換熱系數的分布；再將有限元法與模型降階法相結合，開發快速計算程序，最后通過Matlab/Simulink軟件實現熱與電氣的聯合仿真，以有效解決復雜工況的瞬態計算問題。

1　溫升試驗

1.1　試驗裝置

某地鐵車輛牽引逆變器采用二電平電壓型直—交逆變主電路，其主要參數為：額定電壓DC750 V，額定輸出容量600 kVA，輸出電壓0～585 V，輸出頻率0～160 Hz，開關頻率500 Hz，額定輸出電流600 A，牽引工況最大輸出電流有效值884 A，制動工況最大輸出電流有效值1 156 A，額定工作點效率0.98，采用直接轉矩控制方式。當車輛處于牽引工況時，直流電經過高壓電器箱、濾波電抗器箱分別對2個IBCM60G1型變流模塊供電，經牽引逆變器輸出三相變壓變頻的交流電向4臺異步牽引電機供電。當車輛處于再生制動工況時，牽引逆變器將異步牽引電機輸出的三相交流電變成直流電并反饋回電網，或由制動電阻消耗掉。三相交流電逆變及電阻制動消耗環節的開關管均為FZ1600R17KF6C-B2型IGBT模塊。

考慮到IGBT模塊的芯片被絕緣材料封裝起來，無法對其直接進行溫度測量，因此在熱管散熱器的安裝面上布置PT100熱電阻進行溫度測量。熱管散熱器上測溫點的布置情況如圖1所示。圖中：V2—V7和V1，V8分別為實現三相逆變和電阻制動功能的IGBT模塊；J1—J3為溫度繼電器；1#—6#為相鄰的IGBT模塊間的測溫點；7#為J2的測溫點。

圖1　測溫點布置情況

在實驗室條件下進行溫升試驗的基本步驟為：首先在變流模塊組裝之前于熱管散熱器上布置測溫點，然后將其與總裝后的牽引逆變器、通風機、風罩、電源和負載(牽引電機)等相連，再將測溫點的數據線連接至溫度巡檢儀和計算機，最后進行試驗測試和數據分析。

考慮到實驗室條件下不能真實模擬走行風且只有1臺牽引電機作為負載，因此重點研究在減小變流模塊1的輸入電流時熱管散熱器的溫升情況。在變流模塊1的翅片部分設計1個風罩，通過軸流通風機進行吹風，連接通風機的風罩部分為圓形，包裹翅片的風罩部分為矩形，風罩中間部分采用漸變的形式并設置整流隔柵，以使通風機的出風盡量均勻地吹向熱管散熱器。在風罩入口處布置1個熱電偶，用于測量牽引逆變器附近的空氣溫度。搭建的試驗裝置如圖2所示。

圖2　試驗裝置

1.2　試驗結果

在風罩入口和出口處分別測得9個點的風速值，如圖3所示。由圖3可以看出：與入口處其他部位相比，中心點處的風速因通風機的阻擋而偏小，入口上部的風速高于下部，而冷卻空氣經過通風機、風罩、熱管散熱器翅片及外罩后，出口上部的風速低于下部，出口處風速與入口處風速不對應的情況說明風罩內的空氣流動是非常復雜的。

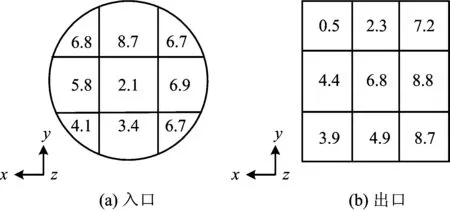
圖3　風罩入口和出口處的風速測量結果(單位： m·s-1)

根據風罩入口處的風速測量結果，可以計算出平均風速約為5.7 m·s-1。

圖4為由各測溫點得到的溫度變化曲線。由圖4可以看出：試驗開始后0～30 min內溫度上升速度很快，30 min后上升速度逐漸變緩；風罩入口處空氣的溫度為31.1 ℃，持續試驗220 min后升為33.8 ℃，這是由于試驗場地的空間較為狹窄，變流模塊1產生的熱量難以有效耗散至實驗室外部，且牽引逆變器周圍還存在其他工作中的試驗設備，導致風罩入口處的空氣溫度不斷上升；隨著試驗時間的推移，各測溫點的溫度與風罩入口處空氣溫度的差值趨于平穩，說明熱管散熱器的溫升達到了平衡狀態，因此風罩入口處空氣溫度的變化在試驗誤差允許范圍內；測溫點中4#的溫度最高、3#的溫度次之，而6#的溫度最低，這主要是由于V1和V8未工作且處于冷卻空氣上游、持續工作的V4和V5處于冷卻空氣最下游所致。

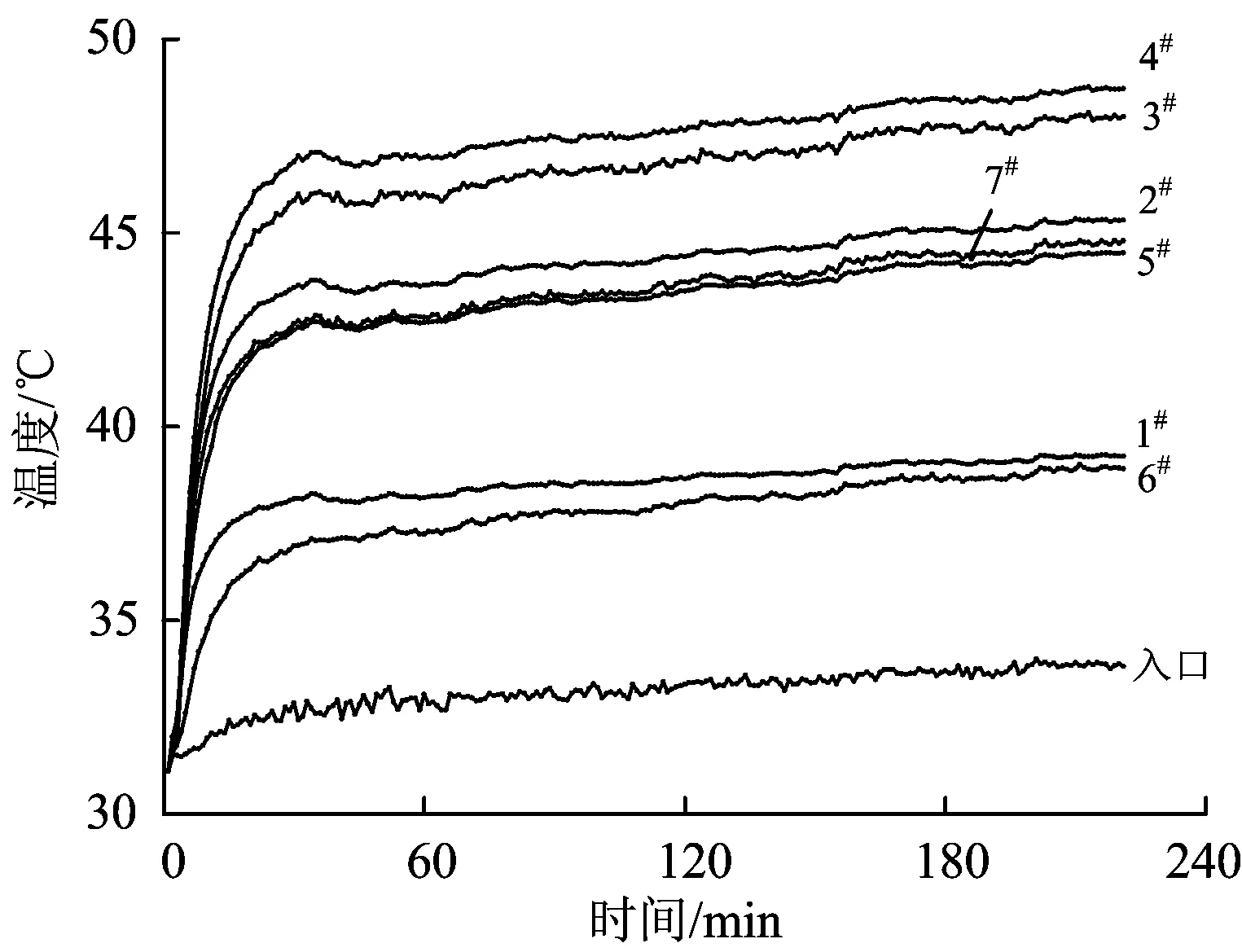
圖4　溫升試驗得到的溫度變化曲線

2　CFD穩態熱仿真分析

2.1　CFD仿真模型

熱管散熱器內部涉及復雜的相變過程，目前還很難對其本身進行數值模擬。較為常用的方法是將熱管假設為軸向導熱系數很高、徑向導熱系數為熱管材料導熱系數的實體棒桿[4-6]。由于IGBT模塊中包含AlSiC基板、焊料、銅層、AlN基片、芯片和絕緣材料，因此結合各層材料的厚度和整個模型的復雜程度，將仿真模型中網格的基本尺寸設置為2 mm，遠離熱管散熱器的流體區域網格尺寸設置為5 mm。以風罩為參照，將被風罩包裹的變流模塊1的流體外邊界設置為壁面邊界條件；變流模塊2因為沒有被外罩包裹，故將其流體區域適度擴大，并將其流體外邊界設置為壓力出口條件。利用HyperMesh軟件建立六面體為主的高質量網格，數量為3 862萬個，其中流體區域的網格數量為2 520萬個。

為便于熱仿真結果與溫升試驗數據的對比，以溫升試驗條件作為熱仿真計算的輸入條件。考慮到風罩內的空氣流速分布極為不規則，為簡化仿真條件的參數設置，將風罩入口處的風速設為5.7 m·s-1、空氣溫度設為33.8 ℃。假設冷卻空氣在風道內的流動狀態為完全湍流，采用標準k—ε模型進行模擬。利用FLUENT軟件和DELL T7600臺式工作站對CFD仿真模型進行穩態計算，可以得到收斂的仿真結果。

2.2　穩態仿真結果

圖5為冷卻空氣在試驗裝置內流動時不同截面處冷卻空氣的流速分布云圖。由圖5可以看出：冷卻空氣受熱管散熱器翅片、熱管和外罩的阻擋，在不同部位處的流速分布并不相等，在局部截面面積小的區域其流速可達到最大值，為16.61 m·s-1。

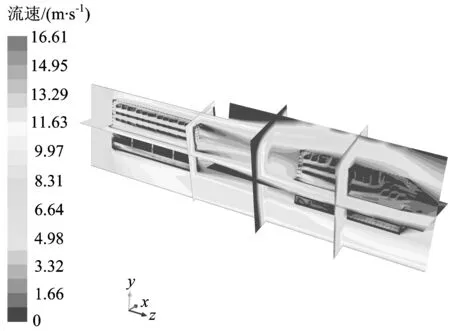
圖5　不同截面的冷卻空氣流速分布云圖

圖6為經過87 h仿真計算得到的變流模塊1的熱管散熱器及IGBT模塊溫度場分布云圖。由圖6可以看出：因冷卻空氣主要沿z坐標軸正方向流動，處于冷卻空氣最下游的V4和V5這2個IGBT模塊的溫度最高，可達55.43 ℃；V1和V8模塊的溫度最低，這是由于它們不發熱且位于冷卻空氣的上游；1#—7#測溫點的溫度分別為39.65，45.81，49.02，48.95，45.61，39.49和45.33 ℃，其中3#點的溫度略高于4#點的，這與溫升試驗結果有區別的主要原因是試驗中通風機入口處冷卻空氣的風速不均勻，而仿真時假設入口處的冷卻空氣風速完全相等；對比仿真結果與試驗數據可知，各測溫點溫度的相對誤差不超過5%，說明仿真結果的準確性。

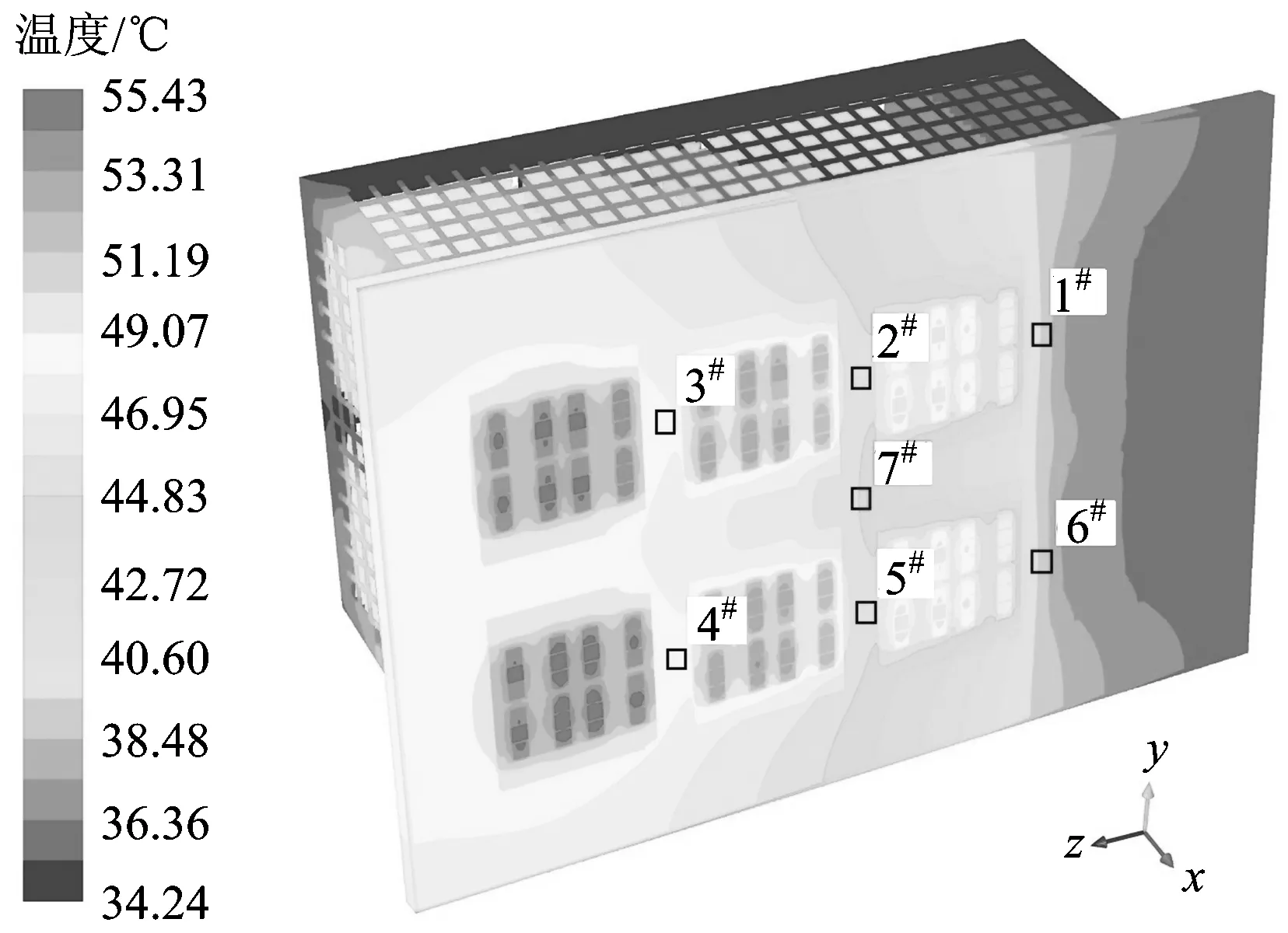
圖6　熱管散熱器及IGBT模塊的溫度場分布云圖

圖7為變流模塊1的熱管散熱器對流換熱系數分布云圖。由圖7可以看出：冷卻空氣流經散熱片、熱管、外罩和底板時，會產生不同程度的對流換熱作用，從而表現出對流換熱系數值的差異，即對流換熱系數的分布并不一致；對流換熱系數值大的區域表示對流換熱較為充分，反之則不充分。

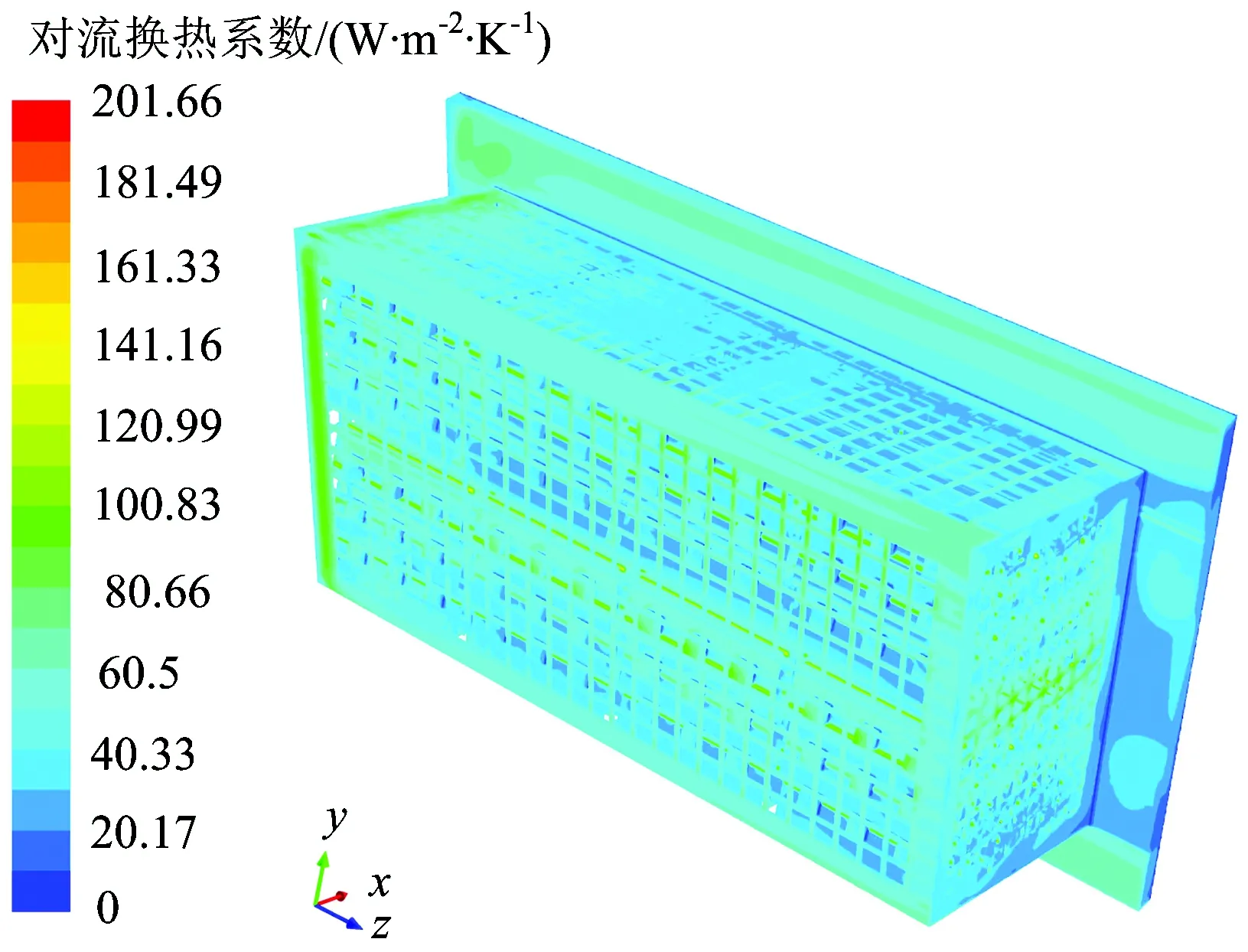
圖7　熱管散熱器的對流換熱系數分布云圖

對流換熱系數分布處于CFD模型中流體和固體相接觸的流固耦合面上，流體與固體之間的熱量通過這些面進行傳遞，因此在有限元模型只需考慮固體和流固耦合面的換熱，則對流換熱系數分布是有限元模型中非常關鍵的邊界條件。在大多數有限元法和模型降階法的工程應用中，將邊界條件即對流換熱系數設為常數，這種處理方式與實際情況有差異，這也是有限元法的計算精度低于有限體積法的根本原因。

3　快速瞬態熱仿真分析

3.1　理論基礎

圖6所示的溫度場分布是經過較長計算時間得到的穩態結果，而圖4所示的溫度變化曲線是通過溫升試驗得到的瞬態數據，故為了更好地實現仿真結果與溫升試驗數據的對比，需要進行瞬態熱仿真。考慮到CFD仿真的準確性高但計算效率非常低，故在滿足計算精度的前提下為進一步實現熱管散熱器和IGBT模塊瞬態導熱問題的快速計算，可將圖7所示的對流換熱系數分布插值至有限元模型中，以保證有限元模型與CFD仿真模型的邊界條件一致，再結合有限元法及模型降階法中最基本和最重要的Krylov子空間法[8-11]進行程序開發。

利用有限元法計算熱管散熱器和IGBT模塊等固體區域的溫度場時，瞬態導熱問題的微分方程為

(1)

式中：ρ為密度；cp為定壓比熱容；T為溫度；t為時間；λx，λy和λz為沿物體3個主方向的導熱系數；q為物體內部的熱流密度。

有限元模型的邊界條件分為給定溫度、給定熱流密度和給定對流換熱系數3種。由微分方程等效積分形式的伽遼金提法，在空間域離散后得到包含n個有限元模型節點數目的1階常微分方程組矩陣方程如下。

(2)

式中：Cp為熱容矩陣；K為熱傳導矩陣；P為溫度載荷列陣；φ為節點溫度列陣。

式(2)涉及到大規模矩陣運算，消耗的計算機資源較大，Krylov子空間法可以將物理模型的大規模狀態空間投影到以1組基矢量為特征的低維空間(降階階數r通常取5～50，主要取決于時間步長[12]，該數值遠小于原有階數n)，從而有效降低矩陣的維度，并在保證計算結果準確性的基礎上大幅度降低計算規模來提高計算效率。

3.2　快速計算程序

文獻[13]介紹了模型降階法在IGBT風冷散熱器上進行瞬態問題快速計算的算例，并給出了提取熱傳導矩陣及熱容矩陣、求解降階模型的部分源程序。針對算例中只能計算單一熱源、不同軟件間手動操作、計算效率存在提升空間等問題，本文進行了改進并開發了快速計算程序。具體為：針對不同的IGBT模塊芯片依次設置不同熱源的參數并提取相應的矩陣文件，降階后的矩陣使用常微分方程求解器進行求解，然后將結果投影到原模型上。通過時間步與循環功能重復熱源設置、求解和投影等步驟，自動實現多熱源多載荷步的瞬態計算，其中的時間步由固定步長改為變步長，大幅度減少載荷子步的計算量。借助Matlab軟件的調用功能實現程序的自動化，大大簡化程序使用的復雜度。使用GRUS稀疏矩陣求解器的算法代替Matlab軟件自帶的矩陣分解算法，從而進一步提高了模型降階法的計算效率。

3.3　仿真與試驗的對比分析

利用HyperMesh軟件，網格基本尺寸取8 mm，將變流模塊1的熱管散熱器和IGBT模塊劃分為如圖8所示的有限元粗糙網格，其中單元數目為212 125個，節點數目為165 560個。

將圖7所示的對流換熱系數分布插值到有限元模型的流固耦合面上，且以試驗工況為輸入條件，冷卻空氣的初始溫度取33.8 ℃，利用ANSYS軟件可以在1 min內計算出如圖9所示的穩態溫度場分布云圖。由圖9可以看出：V4模塊的芯片溫度最高，為55.105 ℃，1#—7#測溫點的溫度分別為39.46，45.58，48.82，48.72，45.38，39.30和45.11 ℃，與圖6所示的CFD仿真結果相比，溫度云圖分布規律一致且溫度值的差異小于1%，說明將由精細網格CFD模型得到的對流換熱系數分布插值到粗糙網格有限元模型是非常有效的，這可以說明此步驟使有限元模型的計算規模急劇減小，計算速度提高了數千倍。根據牛頓冷卻定律可知，通過對流換熱系數的引入，可以將風冷、水冷等所有的對流換熱過程以簡單的規律進行描述，因此，利用較少數量的有限元粗糙網格和對流換熱系數插值的方法進行瞬態熱仿真，可以推廣應用到其他類型的對流換熱應用中。

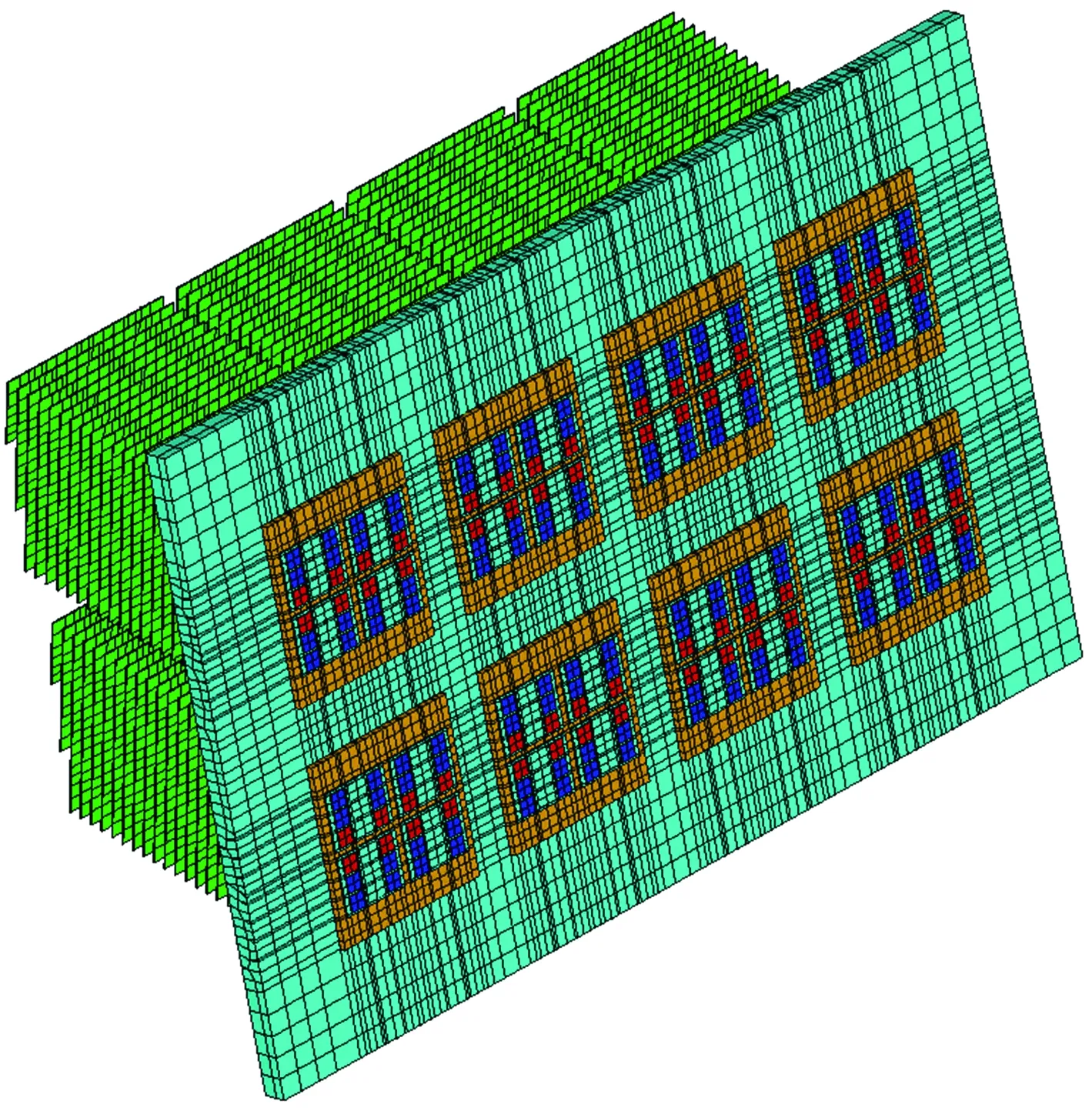
圖8　有限元網格

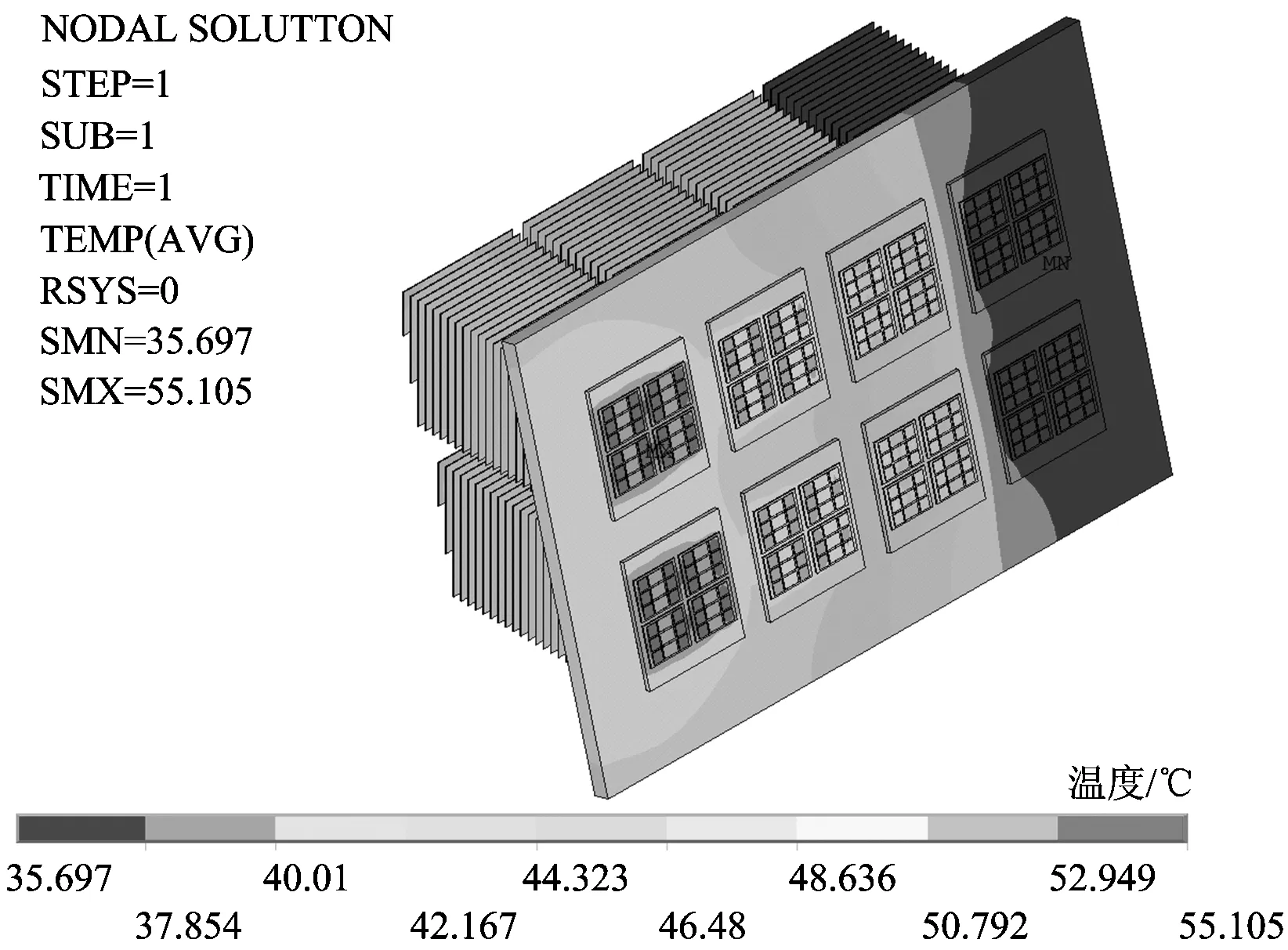
圖9　基于對流換熱系數插值的有限元模型溫度場分布云圖

取降階階數為5，利用快速計算程序對圖8所示的有限元模型進行時間范圍為0～10 000 s的瞬態計算，可用2 min左右計算出如圖10所示的熱管散熱器的溫升曲線。由圖10可以看出：在0～1 000 s時間范圍內溫度迅速上升，之后溫度上升的速度變緩，10 000 s時刻的溫度處于完全穩定狀態；將圖10所示的仿真結果與圖9所示的穩態溫度場結果進行比較，發現最高溫度和1#—7#測溫點的溫度計算結果完全一致，說明快速計算程序所用方法的可行性與準確性。

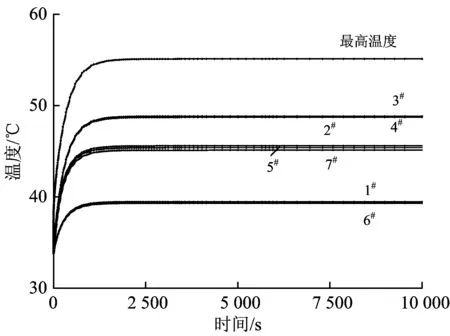
圖10　基于快速計算程序的溫升曲線

在時間范圍相同的條件下，利用ANSYS軟件對圖8所示的有限元模型進行瞬態計算，則需要耗時約5 h才能得到如圖11所示完全一致的溫升曲線，說明筆者開發的快速計算程序的計算準確性和計算效率很高。

4　電氣—熱聯合仿真

4.1　電氣仿真

由IGBT模塊的用戶手冊可知，其損耗與電流、管壓降及結溫有關，因此可將導通電壓、開通損耗等曲線擬合成二次函數[14-15]。在選用Matlab/Simulink的SimPowerSystems模型庫建立地鐵車輛主電路的電氣仿真模型時，IGBT模塊的損耗等復雜工況的計算常使用線性化的參數，而不是實際的隨二次函數變化的參數，這不利于反映電流周期及暫態變化對功耗波動的影響，因此下面對IGBT模塊的損耗計算方法進行改進。

IGBT模塊的損耗來自IGBT芯片和二極管芯片。其中，對于IGBT芯片主要計算其導通狀態下的損耗以及開通和關斷過程中的開關損耗，而忽略其關斷狀態下的損耗；對于二極管芯片主要計算其導通狀態下的和反向恢復過程中的損耗，而忽略其關斷狀態下的和開通過程中的損耗。

以單個橋臂上管IGBT芯片為例，當IGBT模塊的電流大于0時，通過擬合的二次函數計算出電流通過該模塊時的開關損耗，以下管IGBT芯片脈寬調制下降沿判斷單次開關是否結束，開關結束時則累加而得IGBT模塊的開關損耗。通過擬合的二次函數計算電流流過模塊時的導通功率，再經過積分得到IGBT模塊導通損耗。將IGBT模塊開關損耗和導通損耗進行累加，再計算出1個周期內的損耗平均值，即為IGBT芯片的平均損耗。以單個橋臂上管二極管芯片為例，當IGBT模塊的電流小于0時，通過查找導通功耗表得出電流通過該模塊時的導通功率值，然后再積分得到導通損耗。當橋臂輸入電流大于0時，通過擬合的二次函數計算開關損耗，以下管二極管脈寬調制上升沿判斷上管二極管是否反向恢復，二極管反向恢復時則累加而得到二極管反向恢復損耗。將二極管導通功耗和反向恢復損耗進行累加，再計算出1個周期的損耗平均值，即為二極管芯片的平均損耗。其他IGBT模塊損耗的計算與上管相同，不做贅述。

圖11為在電機的全速范圍(電機轉速在20 s內從0加速至300 rad·s-1)內，利用主電路電氣仿真得到的電機電磁轉矩和IGBT模塊損耗隨時間變化的曲線。

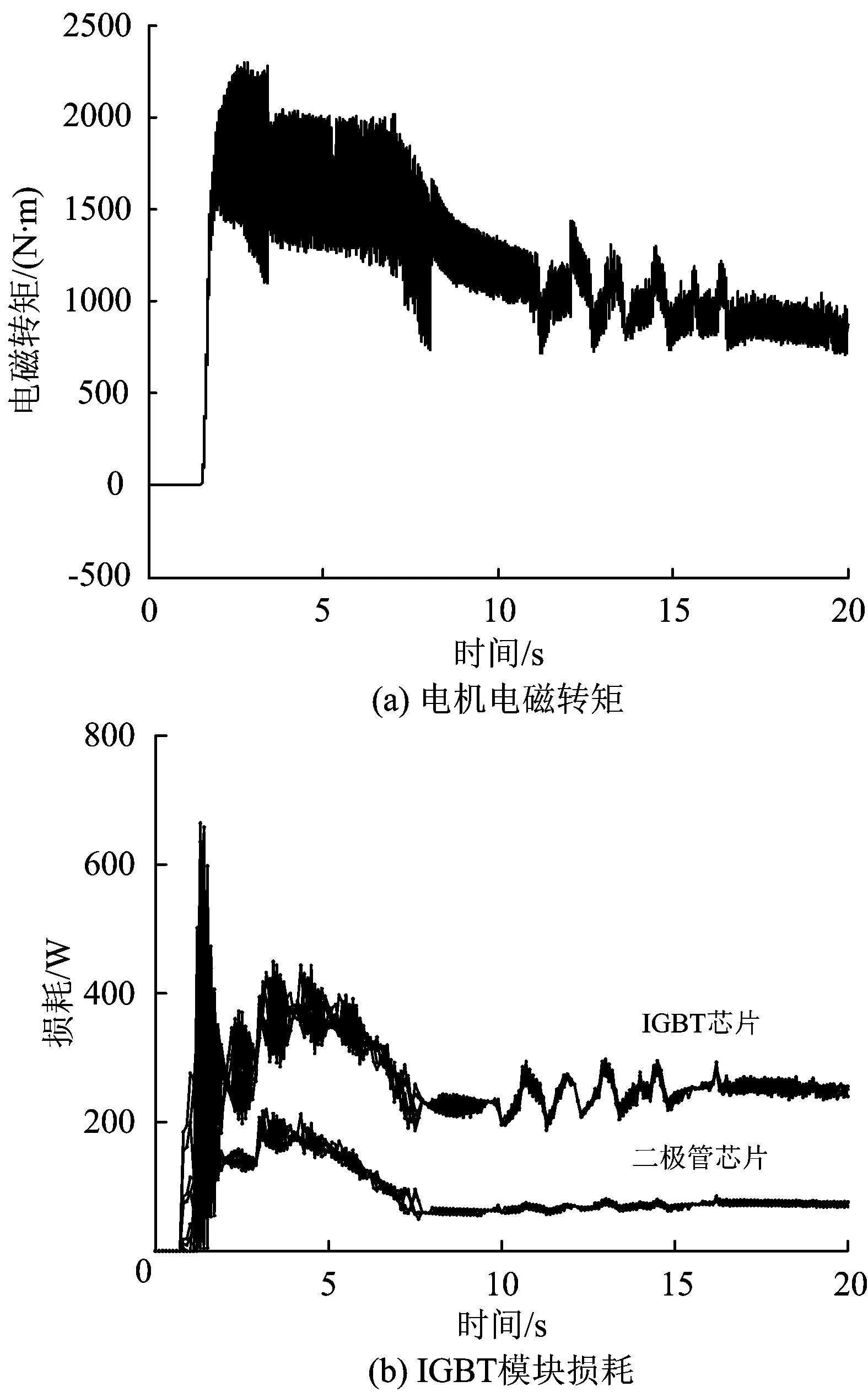
圖11　電機全速范圍內的主電路電氣仿真結果

4.2　瞬態熱仿真

以圖11(b)所示的IGBT模塊損耗數據為快速計算程序的輸入，對圖8所示的有限元模型進行瞬態計算，可在7 min內計算出如圖12所示的溫升曲線。由圖12可以看出：V2—V7的芯片在不同時刻產生變化的損耗，可以直接影響其溫度的響應；熱管散熱器安裝面上的各測溫點因稍遠離產生損耗的芯片，相應的溫度受到的影響較小；V1和V8距離產生損耗的芯片較遠，相應的溫度受到的影響最小，這除與距離熱源的遠近有關外，還與熱管散熱器底板具有較大的熱容量有關。

圖12　全速范圍的溫升曲線

以圖11(b)所示的IGBT模塊損耗數據為ANSYS軟件的輸入，對圖8所示的有限元模型進行瞬態計算，可得到與圖12完全一致的計算結果，但計算消耗的時間長達34.7 h，說明筆者開發的快速計算程序具有很高的計算效率和準確性，與電氣聯合仿真可為解決復雜工況的瞬態熱仿真問題提供有力支持。

5　結　語

針對某地鐵車輛牽引逆變器的IGBT模塊和熱管散熱器的溫升問題，首先在實驗室條件下完成了溫升測試，然后以試驗結果為輸入開展了CFD穩態熱仿真、快速瞬態熱仿真和電氣—熱聯合仿真，試驗數據及不同的仿真方法驗證了筆者開發的快速計算方法可同時滿足計算效率與計算精度的要求，為解決復雜的瞬態熱仿真問題提供了1種新的途徑。

[1]LUTZ J, SCHLANGENOTTO H, SCHEUERMANN U, et al. Semiconductor Power Devices, Physics, Characteristics, Reliability[M]. Berlin: Springer-Verlag Berlin Heidelberg, 2011, 380-409.

[2]CIAPPA M. Selected Failure Mechanisms of Modern Power Modules[J]. Microelectronics Reliability, 2002 (42): 653-667.

[3]HAMIDI A, KAUFMANN S, HERR E. Increased Lifetime of Wire Bond Connections for IGBT Power Modules[C]//16th IEEE Applied Power Electronic Conference and Exposition(APEC). Anaheim: IEEE, 2001: 1040-1044.

[4]丁杰, 唐玉兔. 地鐵牽引變流器的熱管散熱器的數值模擬[J]. 大功率變流技術, 2012 (5): 31-33.

(DING Jie, TANG Yutu. Numerical Simulation of Heat-Pipe Radiator for Metro Vehicle Converter[J]. High Power Converter Technology, 2012(5): 31-33. in Chinese)

[5]PERPINA X, JORDA X, VELLVEHI M, et al. Long-Term Reliability of Railway Power Inverters Cooled by Heat Pipe-Based Systems[J]. IEEE Tractions on Industrial Electronics, 2011, 58(7): 2662-2672.

[6]唐強. IGBT元件熱管冷卻傳熱性能的實驗與數值研究[D]. 蘭州: 蘭州交通大學, 2013.

(TANG Qiang. Experimental and Numerical Analysis on Heat Transfer Performance of Heat Pipe Cooling for IGBT Component[D]. Lanzhou: Lanzhou Jiaotong University, 2013. in Chinese)

[7]YUN Chansu, MALBERTI P, CIAPPA M, et al. Thermal Component Model for Electrothermal Analysis of IGBT Module Systems[J]. IEEE Transactions on Advanced Packaging, 2001, 24(3): 401-406.

[8]蔣耀林. 模型降階方法[M]. 北京: 科學出版社, 2010.

[9]WILHELMUS H A Schilders, HENK A van der Vorst, JOOST Rommes. Model Order Reduction: Theory, Research Aspects and Applications[M]. Berlin: Springer, 2008.

[10]TAMARA Bechtold, EVGENII B Rudnyi，JAN G Korvink. Dynamic Electro-Thermal Simulation of Microsystems-a Review[J]. Journal of Micromechanics and Microengineering, 2005, 15(11): 17-31.

[11]RUDNYI E B, KORVINK J G. Model Order Reduction for Large Scale Engineering Models Developed in ANSYS[J]. Lecture Notes in Computer Science, 2006, 3732(1): 349-356.

[12]YANG Y J, YU C C, SHEN K Y. MEMS Heat Transfer Arnoldi-Based Macromodels and the Study of Minimum Required Orders[J]. Tamkang Journal of Science and Engineering, 2005, 8(3): 185-190.

[13]丁杰, 唐玉兔. 模型降階方法在瞬態熱仿真中的應用[J]. 機車電傳動, 2014(5): 51-55，65.

(DING Jie, TANG Yutu. Application Research of Model Order Reduction Method in Transient Thermal Analysis[J]. Electric Drive for Locomotives, 2014 (5): 51-55，65. in Chinese)

[14]白保東, 陳德志, 王鑫博. 逆變器IGBT損耗計算及冷卻裝置設計[J]. 電工技術學報, 2013, 28(8): 97-106.

(BAI Baodong, CHEN Dezhi, WANG Xinbo. Loss Calculation of Inverter IGBT and Design of Cooling Device[J]. Transactions of China Electrotechnical Society, 2013, 28(8): 97-106. in Chinese)

[15]楊寧, 宋術全, 李紅. 高速動車組輔助變流器箱體的熱仿真設計方法[J]. 中國鐵道科學, 2013, 34(3): 87-92.

(YANG Ning, SONG Shuquan, LI Hong. Thermal Simulation Design Method for the Auxiliary Converter Case of High-Speed EMU[J]. China Railway Science, 2013, 34(3): 87-92. in Chinese)