基于無刷直流電機的伺服系統低速性能仿真研究

王 括，田勝利，李 清，王 鑫

（北京精密機電控制設備研究所，北京，100076）

基于無刷直流電機的伺服系統低速性能仿真研究

王 括，田勝利，李 清，王 鑫

（北京精密機電控制設備研究所，北京，100076）

伺服系統低速運動時，無刷直流電機轉速低，運動平穩性差，容易產生力矩波動，引起低速爬行現象。為解決這一問題，在伺服系統位置環的基礎上引入電流環，其中電流環采用分時反饋策略，根據霍爾信號邏輯對三相電流進行選擇；位置環采用神經網絡比例、微分、積分控制，并仿真驗證伺服系統性能。仿真表明通過雙閉環及神經網絡PID控制能較好改善系統性能。

低速；雙閉環；分時反饋；神經網絡PID

0 引 言

機電伺服系統是以電動機為動力驅動元件的伺服系統，目前廣泛應用于火箭、導彈、機器人等領域[1]。與有刷電機相比，無刷直流電機采用電子換相，消除了機械電刷帶來的摩擦影響；與永磁同步電機相比，無刷直流電機控制不必進行復雜空間矢量變換，控制方法簡單，且其永磁體為均勻的瓦片形結構，較易制造，因此無刷直流電機在機電伺服系統中的應用越來越廣泛[2～7]。

由于電機力矩存在波動，受摩擦、電機換相、驅動電路等限制，伺服系統低速運行過程中經常出現爬行現象，因此引入電流閉環限制力矩波動[8]。

對于大部分機電伺服系統，應用傳統比例、微分、積分（Proportion Integral Derivative，PID）控制通常可以滿足其要求，PID控制結構簡單，對誤差控制有魯棒性，通過調整比例、積分、微分系數可以改變系統的響應特性。然而實際伺服系統中通常存在非線性、參數的時變及不確定性，因此傳統PID可能無法適應高性能指標的要求。

近年來，神經網絡發展迅速，在醫學、圖像處理、人工智能等領域已有廣泛應用。人工神經網絡可以逼近任意復雜的非線性關系，然而單純的神經網絡控制存在對初值選擇敏感、不易收斂等弊端，因此將神經網絡與PID控制結合運用。通過反向傳播（Back Propagation，BP）神經網絡在線調整比例、積分、微分系數，選擇合適的初值使其達到收斂效果。

本文通過采集相電流并通過霍爾信號得到電流分時反饋，位置環采用神經網絡PID控制，通過仿真與普通PID控制進行對比，達到優化效果。

1 無刷直流電機伺服系統

機電伺服系統通常由電機、控制器、驅動器、傳感器、傳動裝置等組成，位置-電流雙閉環系統結構如圖1所示。

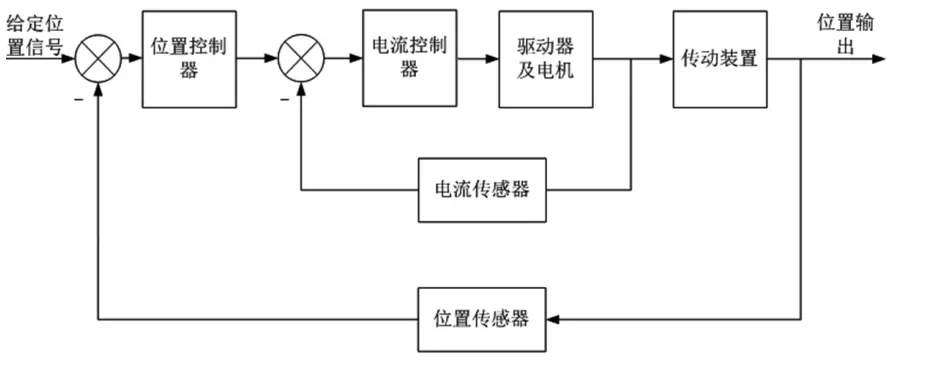
圖1 伺服系統結構

根據無刷直流電機原理建立電壓、電流與轉矩方程：

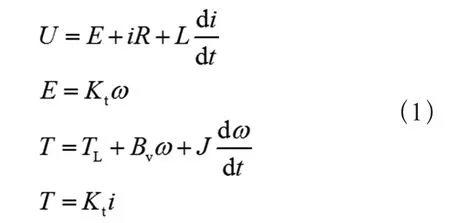
式中 U為母線電壓；ω為電機轉速；i為相電流；E為感應電動勢；T為電磁轉矩；L為電樞電感；R為電樞電阻；Kt為轉矩系數；J為轉動慣量；TL為負載轉矩；Bv為阻力系數。

忽略負載力矩，并經過拉普拉斯變換及簡化得到電機轉速與電壓關系的數學模型：

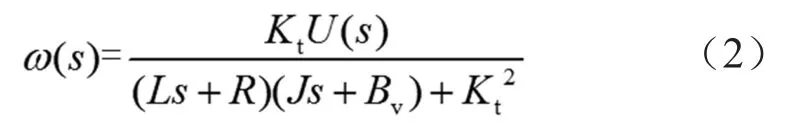
2 分時電流獲取方法

由于伺服系統母線電流中含有控制驅動器消耗的電流，因此需要通過電流采集芯片采集相電流，根據霍爾傳感器信號邏輯可以得到當前時刻導通相，通過模擬通道的數據選擇器可以選出當前正向相電流。

根據霍爾信號邏輯圖得到數據選擇器選通端輸入信號與三相霍爾信號關系式：

式中 B，A為數據選擇器選通端輸入信號；HA， HB，HC為三相霍爾信號邏輯；分別為HA， HC取反。

圖2為電流選擇電路。

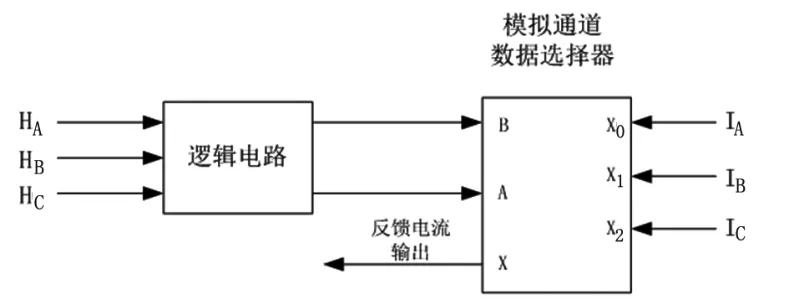
圖2 電流選擇電路

3 基于神經網絡的PID算法

神經網絡PID算法從結構上可以分為輸入層、隱含層、輸出層3層，通過調節神經元網絡權值改變神經網絡輸出即PID參數。圖3為神經網絡PID系統原理。

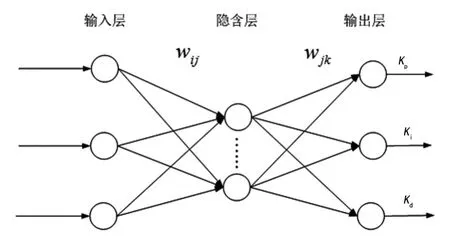
圖3 神經網絡PID原理

隱含層及輸出層的活化函數分別用正負對稱的sigmoid函數和非負的sigmoid函數表示，活化函數能夠增強網絡的映射功能，同時提高收斂速度。取性能指標函數其中，r(k)為位置指令輸入；y(k)為位置反饋；e(k)為誤差。根據最速下降法修正網絡權值系數，沿負梯度方向搜索，控制策略采用加入慣量項的方法，使BP網絡訓練時振蕩較小。權值修正公式為

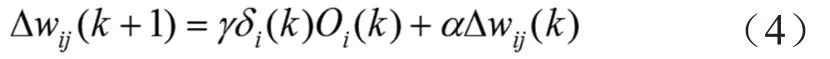
式中 Δwij為網絡間權值的變化量；Oi為第i個神經元的實際輸出；δi為第i個神經元的權值修正的局部梯度；γ為學習速率；α為慣量因子。

采用直接PID控制，根據梯度運算方法可得輸出層局部梯度：

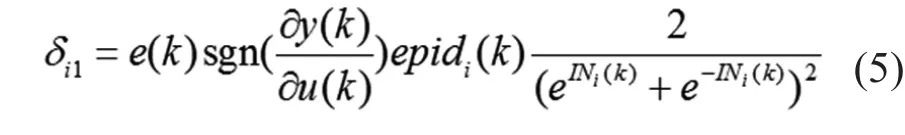
式中 INi(k)為輸出層神經元的輸入；u(k)為PID控制輸出；y(k)為位置反饋；epidi(k)(i=1,2,3)分別為位置誤差、位置誤差變化率、位置誤差積分。

隱含層局部梯度：

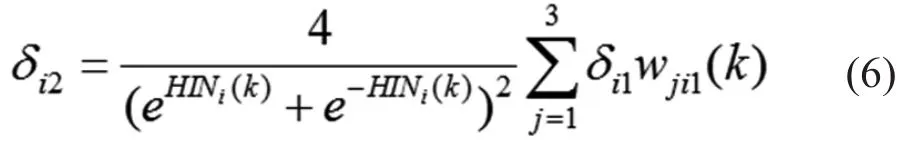
式中 HINi(k)為隱含層神經元輸入；wji1(k)為輸出層權值。

根據以上分析，在本文中BP神經網絡PID控制算法在Simulink中可以通過下述步驟進行：

a）步驟1：選定BP網絡結構為3-5-3，即3個輸入層神經元，5個隱含層神經元，3個輸出層神經元。給出各神經元權值的初值，均選取為0.5，同時選定學習速率η=0.99，慣性系數α=0.000 1；

b）步驟2：采樣得到位置指令r(k)，位置反饋y(k)，計算e(k)=r(k)-y(k)。

c）步驟3：計算BP神經網絡各層神經元輸入、輸出值，其中輸出層的輸出為控制參數Kp，Ki，Kd。

d）步驟4：采用直接式PID控制，根據誤差e(k)計算出控制量輸出u(k)，u(k)=Kp.e(k)+Ki.Σe(k)+Kd. (e(k)-e(k-1))。

e）步驟5：進行神經網絡在線學習，根據權值修正公式得到修正后的權值。

f）步驟6：令k=k+1，返回步驟2。

系統采用電流環與位置環雙閉環控制，由于位置環對系統產生決定性影響，因此位置環應用神經網絡PID控制與普通PID進行比較，電流環控制采用比例、積分（Proportion Integral，PI）控制。

4 仿真結果

根據機電伺服系統原理建立主要包括控制器模塊、脈沖寬度調制（Pulse Width Modulation，PWM）產生模塊、功率管邏輯開關模塊、三相驅動模塊、電機本體模塊、機械傳動模塊的整體伺服系統，其Simulink模型如圖4所示。

圖4 雙閉環系統Simulink模型

選用maxon某型號電機，電機及傳動機構折算至電機軸上的轉動慣量為2.7×10-7kg·m2，其中，相間電阻ra=2.71 Ω，相間電感La=2.31×10-4H，反電動勢系數ke=0.013 3 (V·s)/rad，轉矩系數KT=0.013 3 (N·m)/A，阻力系數Bv=5×10-9N·m·s。為與實際系統對應，選擇位置反饋信號采樣時間為1 ms，分辨率為0.01°，摩擦采用Stribeck模型作為負載力矩疊加至系統中。電流采集部分通過前文所述方式，采集三相電流并進行選擇，得到電流反饋。

位置控制器分別應用普通PID和神經網絡PID，在參數初值相同情況下進行小角度位置信號仿真。初值選取Kp=10，Ki=0.05，Kd=0.024神經網絡PID參數浮動范圍為Kp=5～15，Ki=0.025～0.075，Kd=0.012～0.036。

輸入0.1°，4 Hz正弦信號，圖5、6分別為神經網絡PID及普通PID仿真結果。由于位置指令角度較小且頻率不高，因此可以認為伺服系統處于低速運行狀態，可以明顯看到普通PID平頂寬度較大，同時相角滯后較小。圖7為神經網絡PID參數變化。

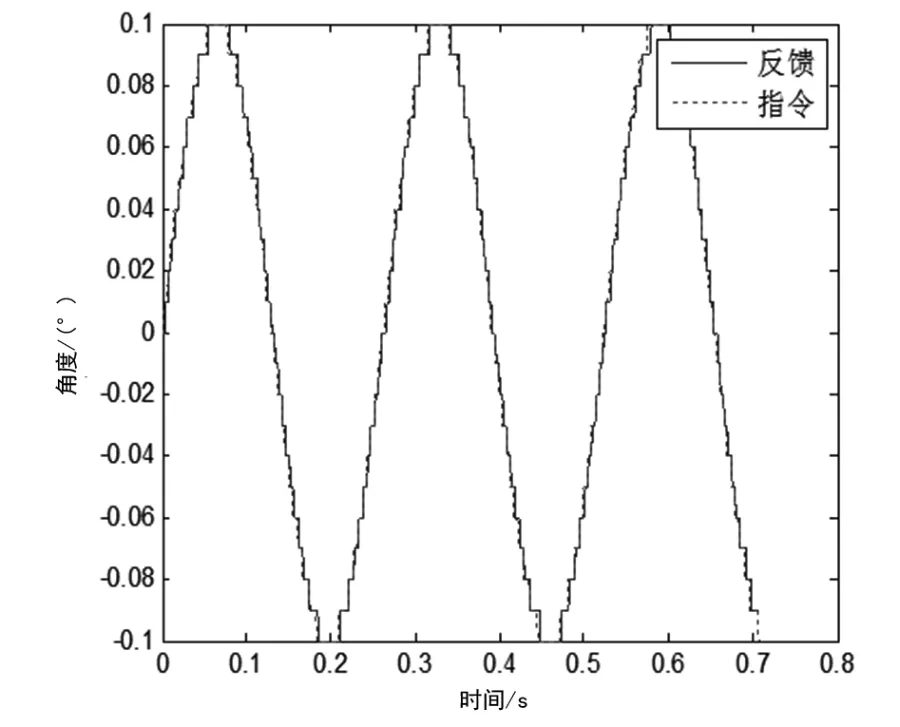
圖5 0.1°，4Hz神經網絡PID控制

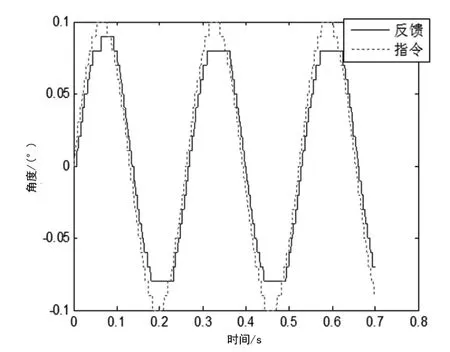
圖6 0.1°，4Hz普通PID控制

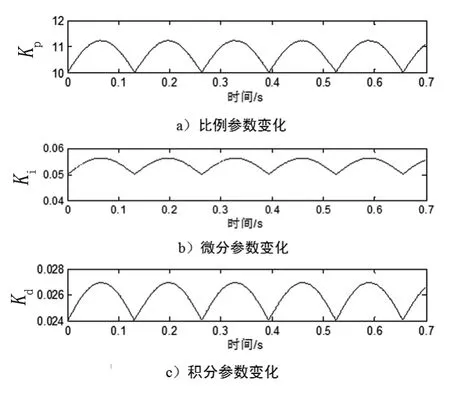
圖7 神經網絡PID參數變化

5 結束語

根據仿真結果可以看出，位置輸入為小幅值正弦信號時，神經網絡PID能實時改變PID參數，更好地跟蹤給定信號，改進系統的低速性能。同時可以看出PID參數隨時間變化曲線，其趨勢為指令速度低時增大控制參數，使得系統對小誤差信號響應效果更好。

[1] 黃玉平, 李建明, 朱成林. 航天機電伺服系統[M]. 北京: 中國電力出版社, 2013.

[2] 夏長亮. 無刷直流電機控制系統[M]. 北京: 科學出版社, 2009.

[3] 深秀風. 永磁無刷直流電機電磁轉矩脈動抑制技術的研究[D]. 哈爾濱:哈爾濱理工大學, 2009.

[4] 王亮, 宗元. 電機低速運行“爬行”現象的研究[J]. 儀器儀表與分析監測, 2011(3): 18-21.

[5] 陶桂林. 無刷直流電機及其系統研究[D]. 武漢: 華中科技大學, 2004.

[6] 周小慶. 高速無人機電動舵機控制器的設計與實現[D]. 杭州: 浙江大學, 2010.

[7] 吳森堂. 飛行控制系統[M]. 北京: 北京航空航天大學出版社, 2005.

[8] Wang S, Li T C, Wang Z G. Commutation torque ripple reduction in brushless DC motor drives using a single current sensor[J]. Electric Machines & Control, 2008, 37(6): 16-17.

Research on the Performance at Low Speed of the Servo System Based on the Brushless Direct Current Motor

Wang Kuo, Tian Sheng-li, Li Qing, Wang Xin
(Beijing Research Institute of Precise Mechatronics and Controls, Beijing, 100076)

When the servo system moves in low speed, there will be low speed of BLDCM, bad motion stability, torque ripple and phenomenon of slow moving. To solve the problem, current loop based on the servo position loop is used. Current feedback in turn can be used in the current loop and the three-phase current can be chose based on Hall signal. Using Neural Network PID controller in the position loop and the system performance will be proved by simulation. The simulation shows that system performance can be improved by double closed-loop and neural network PID.

Low speed; Double closed-loop; Current feedback in turn; Neural network proportion integral derivative

V448.22

A

1004-7182(2016)05-0092-04

10.7654/j.issn.1004-7182.20160519

2016-05-15；

2016-06-08

王 括（1991-），男，助理工程師，主要研究方向為機電伺服機構