小學生計算錯誤的成因分析及應對策略

沈春桃

【關鍵詞】小學生 計算 錯題 成因分析

【中圖分類號】G 【文獻標識碼】A

【文章編號】0450-9889（2016）02A-0011-02

去年9月，我們課題組申報了市基礎教育研究小課題《數學課堂教學中“錯誤資源”的利用研究》。近一年來，成員們時刻關注學生的錯誤，及時收集學生的錯誤情況，分析學生出錯的原因，尋找避免錯誤的策略，并嘗試將學生的錯誤轉變為課堂的有利資源。課題組認為，數學學習活動中學生說錯話，做錯題是正常的。2011年版數學課程標準也指出：讓學生形成堅持真理、修正錯誤、嚴謹求實的科學態度。對于這些計算錯誤，即使教師或家長再三強調，學生仍會經常出現。原因何在？實驗中，我們發現了一些規律性的問題，尋找、分析了造成計算錯誤的七大原因，并總結出一些策略，供同仁參考。

一、概念理解不清晰

計算知識是建立在數學概念的理解基礎之上的，如學生對“數位”“進一位”“退一位”“滿十進一”“借一當十”等一系列相關概念的理解不清晰，就不能根據計算法則、定律、公式、性質等知識正確地進行計算。

例1中，學生計算豎式“3700÷200”時，被除數和除數同時縮小100倍，余數也跟著縮小了100倍，因為余數“1”是在百位上余下來的，表示1個100。這道題反映出學生的位值概念不清晰，當應用商不變性質豎式計算時，缺乏對余數的意義的真正理解。

應對策略：要讓學生切實掌握與計算有關的以下概念知識：1.數的認識：要引導學生理解個位、十位等數位上的數所表示的數值，知道相同的數字在不同的數位上表示的數值是不同的。2.運算定律和運算性質：要幫助學生總結加法、乘法的運算定律及減法、除法的一些運算性質，指導學生利用這些定律和性質來使計算變得簡捷、迅速。3.計算法則：整數、小數、分數的四則運算都有它們獨自的計算法則，每種計算法則都是根據數的意義、性質和運算定律推導出來的。如多位數加法法則“數位對齊，個位加起，滿十進一”學生肯定要知道。4.運算順序：運算順序是在四則混合運算過程中，對運算先后次序的一種規定，它是保證計算正確的前提，必須讓每一個學生都掌握。

二、算理掌握不到位

算理是計算的道理，是計算的依據。算理掌握了，就解決了“為什么這樣算”的問題。教學中教師要幫助學生弄清算理，使學生不僅知其然而且知其所以然，否則，出現錯誤的可能性就大得多。

如例2，被減數個位上“0”不夠減“8”，要向十位借“1”，而十位又是“0”，只能又向百位借“1”，當作10個“十”，10個“十”被個位借走了1個“十”，那么十位上就只剩下9個“十”，“9”減“5”得“4”，不是“5”。因為學生不明上述算理，影響了對連續退減法計算法則的掌握，自然造成錯誤。

應對策略：弄清算理，以理馭法。如果只是通過反復“演練”來達到計算正確、熟練的話，學生終因算理不清、知識遷移的范圍極為有限而無法解決各類計算問題。教學時我們應該通過教具演示說明算理，通過學具操作展示算理，通過聯系實際講清算理，通過展示思路理清算理。

三、常用口算不熟練

口算又稱心算，是指不借助工具直接通過大腦思維想出結果的一種計算方法。2011年版數學課程標準強調“應重視口算，加強估算……”，可見，口算在計算能力培養上具有重要地位。我們認為：口算是筆算的基礎，筆算依靠口算，口算在日常生活中有廣泛的應用。學生如果對口算不熟，就會直接導致整道題的計算錯誤。

例3：64-49=25。在口算退位減法中，學生很容易把十位直接相減，而未考慮到個位夠不夠減的情況。

例4：24×5=100。學生計算這道題時與常用的口算數據“25×4=100”混淆，想當然地把“24×5”當成“25×4”來口算了。

例5中，學生根據數據特征，想靈活運用運算定律或性質自覺進行簡便計算，可對于“多減了要加回去”的口算方法不熟練，又繼續“減2”，自然造成計算錯誤。

應對策略：加強口算，學會估算。1.基本口算要熟練，如“20以內數的進位加法和退位減法”及乘法口訣表內的乘除法，要讓學生達到脫口而出的水平。2.常用數據要熟記，如“25×4=100”，“24×5=120”，“25×8=1000”，3/4=0.75也=75%等。3.簡便口算要自覺，要訓練學生利用數據特征和運算關系，應用定律和性質自覺簡算，如一看到“48×25”，便想到用“（48÷4）×（25×4）=12×100=1200”來算。4.要經常進行口算練習，且應該貫穿于教學活動的全過程，要結合教學內容有針對性、有目的地進行。5.要讓學生養成估算的習慣。無數事實說明：一個人在一天活動中估算和差積商的次數，遠比進行精確計算的次數多得多，算前估一估，方向更明確;算后估一估，結果更準確。

四、式題感知不精細

算式由數據與運算符號組成，因為無情節，外顯形式枯燥，所以難以引起學生的興趣與注意。學生面對算式時往往不夠認真、精細，粗略一看，便下手計算，常將45、208、20002等數當成54、268、2002來算。尤其是不少學生帶著情感色彩看式題，如當學習了“湊0”或“湊整”的簡便計算后，這些方法會對學生的感知產生強刺激，使學生忽略運算的順序、計算的法則，導致計算錯誤。如例6就是典型的受“湊整”方法強刺激影響而忽略運算順序的案例。

例7中，學生看到“12”與“3”正好可以約分，這一特征成了“強刺激”，于是未考慮運算順序便約分計算。

例8中，題目“能簡算的用簡便方法計算”的要求與“3/4-3-4相減又剛好等于0”成了“強刺激”，學生也不想運算的順序怎樣便直接先減再乘了。

應對策略：加強對比，防止負遷移。在學生形成新概念、掌握新知識后，我們要將相近、相似、易混、易錯的內容組織在一起進行對比練習，以便讓學生區別異同，全面感知式題的數據、符號、運算順序等，進一步提高計算能力。如5×9=45，6×9=54;4×9=36，7×9=63;再如“16×5”與“15×6”，“1÷2.5”與“2.5÷1”;又如“13-0.9+0.1”，“2.4-0.4÷2”等。

五、解題意志不堅強

學生在遇到式題數據較大、較為陌生或過于繁雜時，缺乏耐心和堅強意志，內心煩躁，想很快完成計算，便不考慮選擇合理的算法，導致錯誤率提高。如“25.8×0.46+2.58×5.4”，此題乍一看，會給人“山重水復疑無路”的感覺，如果學生不細心審題，綜合運用相關知識，選擇簡便方法，化繁為簡，而只是按運算順序去計算，肯定因為復雜難算而出現大面積的錯誤。

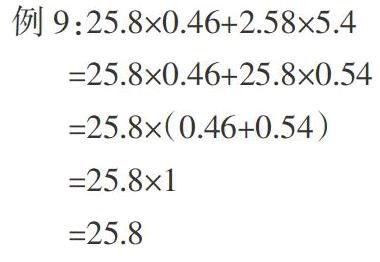
例9中，學生先運用“積的變化規律”，把“2.58×5.4”轉化為“25.8×0.54”或把“25.8×0.46”轉化為“2.58×4.6”，再運用乘法分配律，便能使式題“眉清目秀”，解題心情也能達到“柳暗花明又一村”之快感。

應對策略：分層練習，形式多樣，激發興趣。計算題枯燥乏味，學生當然希望快點完成，尤其當題目涉及數字大、計算復雜時，肯定會缺乏耐心，產生厭煩情緒。因此，設計練習時要分層，由易到難，而且要變換練習形式，刺激學生感官，使學生始終保持積極的心態完成計算。長期訓練，學生的解題意志便會堅強。當然，讓學生樹立責任感、自信心，力爭算一題，對一題，不畏困難也是很有必要的。

六、集中注意不穩定

有的學生容易對計算這種單調乏味的學習產生疲勞，集中注意的穩定性較差，注意的范圍也比較狹窄，尤其是在同一時間內要把注意力分配到多個對象時，極易造成顧此失彼、丟三落四的錯誤。

應對策略：變換形式，強化訓練。根據小學生的年齡及心理特點，教師應創設富于情趣的計算活動，保持學生的注意力。如低年級常采用的“對口令”“接力賽”就是很好的形式。比如，教師出示數字“10”，一個學生說“7”，另一個學生說“3”;一個學生說“2”，另一個學生說“8”;或出示數字“100”，讓學生連續“減8”等。中高年級可常進行一些兩步計算口算題訓練，由教師口述前半題，學生口算出得數后記在腦海里，再看卡片上的后半題，算出最后得數。

七、定勢思維常干擾

定勢思維既有積極影響又有消極影響，積極影響能促進知識正遷移，消極影響則干擾新知的學習。學生在計算時，常常會受固有的思維模式、原有的計算法則干擾，影響新的計算方法的掌握。如剛學習小數加減法時，受整數加減法方法定勢思維影響而導致計算失誤。

學生上課不認真聽老師分析講解，沒有將“相同數位對齊”再加減，做作業時常受“末位對齊”方法影響，出現不必要的錯誤。

應對策略：1.強化審題意識，可訓練學生自問自答如下問題“數字與符號抄對了嗎？”“是什么運算？”“先算什么，再算什么？有簡便嗎？”等。2.在設計練習時，要有意創造克服思維定勢的情境。如無規律編排四則計算的口算題，培養學生具體問題具體分析的習慣。3.要加強對比練習，對比新舊知識，相似或相近的計算等，促使學生在計算中進一步認識四則運算的意義及相互關系，建構完整的認知結構。

以上七種錯誤原因并不是孤立的，而是互相聯系、互相影響，有些錯誤包含了上述多種原因。找到了造成學生計算錯誤的成因就能有針對性地找到解決策略，那么幫助學生減少計算失誤就不再是難事了。

（責編 黎雪娟）