臨界點效應在個人所得稅籌劃中的應用

□文/申永化 謝艷霓

（1.中國重型機械研究院股份公司；2.慶安集團有限公司 陜西·西安）

個人所得稅是調整征稅機關與自然人（居民、非居民人）之間在個人所得稅的征納與管理過程中所發生的社會關系的法律規范的總稱，是以自然人取得的各項應稅所得為對象征收的一種稅。個人所得稅的征稅項目有：工資、薪金所得；個體工商戶生產經營所得；對企事業單位的承包經營、承租經營所得；勞務報酬所得；稿酬所得；特許權使用費所得；財產租賃所得；財產轉讓所得；利息、股息、紅利所得；偶然所得；經國務院財政部門確定征稅的其他所得。不同類型的所得適用不同的費用扣除規定，分別對應不同的稅率和計稅方法。

隨著我國經濟的發展，人們的收入水平不斷提高，需要繳納個人所得稅的人越來越多，對個人征稅的項目也涉及11個項目之多，做好納稅籌劃與個人切身利益密切相關，因此個稅納稅籌劃成為了很多人關注的問題。

按國稅總局《國家稅務總局關于調整個人取得全年一次性獎金等計算征收個人所得稅方法問題的通知》這一規定，行政機關和企事業單位向其員工發放的全年一次性獎金將不再按單獨一個月工資、薪金所得計算納稅，改為將員工當月內取得的全年一次性獎金，除以12個月，按其商數確定適用稅率和速算扣除數。這種計算方法如果運用得當，可以大大減輕個人的納稅負擔。下面結合2011年實行的新個人所得稅法舉例說明一次性發放獎金可以少繳納個人所得稅，及如何做到最優的工資與獎金分配。

（一）

案例1：假定某人年收入100，000元，每月四金數額為800元。

方案① 月工資6000元，獎金28，000元一次性發放：

納稅額=12×［（6000-3500-800）×10%-105］+（28000×10%-105）=2760

方案② 月工資6，000元，獎金28，000元分12次平均發放：

納稅額=11×［（6000+28000/12-3500-800）×10%-105］+［（6000-3500-800）×10%-105］+（28000/12×10%-105）=3475

明顯可以看出，方案①比方案②少交稅715元，一次性發放獎金能夠明顯減輕個人所得稅稅負。

（二）

據筆者了解，目前很多企業都知道全年一次性獎金具有節稅的效果，也紛紛在采用這種辦法，但是他們并沒有意識到在個人全年收入一定的情況下，不同的工資與獎金分配組合對納稅總額也存在很大的影響。

現舉例說明合理分配二者比例的重要性，以（一）中結論為依據，獎金一次性發放。為方便計算，假設在扣除基數3，500元的基礎上暫不考慮應扣除的社保保險等費用。

案例2：某人年收入120，000元，發放組合如以下兩種：

①月工資8，500元，獎金1，8000元。

納稅額=12×［（8500-3500）×20%-555］+18000×3%=5880

②月工資8，499.90元，獎金18，001.2元。

納稅額=12×［（8499.90-3500）×20%-555］+（18001.2×10%-105）=7034.88

以上計算，案例2中組合①明顯優于組合②，組合②中的月工資只比①少0.10元，而個稅則要多納1，154.88元，這兩種差別不大的分配方法造成的納稅差距如此巨大。由此可以看出，當總收入一定時，如何調整工資與獎金之間的比例對納稅產生非常重大的影響，這也是納稅籌劃的關鍵所在。根據筆者調查發現，很多單位在合理避稅方面采取了多種策略，雖然在一定程度上也減少了應繳稅額，但是從合理安排工資與獎金的分配比例來看，并沒有使納稅額最低，以至于無形中讓企業和個人遭受不少損失。幾分錢或幾十元錢的區別往往引發的納稅差額是上百倍，甚至是上千倍，因此如果單位在這方面沒有意識或相應措施，每年多繳納的個稅將是超乎想象的，尤其是對那些高收入階層、職工人數較多的企業而言，這種影響更大。

兩種不同方案繳納個人所得稅的巨大差異引起了筆者的關注，因此更進一步對這一問題進行研究。

為什么案例2中在總收入不變的情況下，差異不大的分配方法會產生如此大的納稅差距？因為在兩種分配方案中，獎金數額雖然相差甚少，但是獎金為18，000元時所對應的稅率按照 1，500（18000/12）對應的稅率來確定，為 3%；為 18，001.2 元時對應的稅率按照1，500.10（18001.20/12）對應的稅率來確定，為10%。獎金的微量變化導致對應稅率的大幅度變化是導致應交個稅差異的根本原因。

（三）

本文就此問題進行進一步探討，企圖尋求一種規則，遵循這一規則在一定數額的年收入中分配工資與獎金（本文暫不考慮任何支出以及其他方面的因素），可以使繳納的稅額最低。

令B=年收入，B＞60000（因為如果年收入小于此數，不管把獎金數額定為多少，只要獎金一次性發放，就能使所交納的所得稅額最低，所以在此不必作討論）；Y=應繳納的個人所得稅額。

設：X為一次性發放的獎金數額，0≤X≤B；月工資=（B-X）/12；M1為月工資扣除費用的余額所對應的稅率，C1為稅率M1對應的速算扣除數；M2為獎金除以12其商數所確定的適用稅率，C2為稅率M2對應的速算扣除數。則：

Y=12｛［（B-X）/12-3500］×M1-C1｝+M2×X-C2

=（M2-M1）X+（B-42000）M1-12×C1-C2

在本假設中，只要X的值確定，M1、M2、C1、C2都可以根據稅率表查出確定值。所以，在X取定一個確定值時，可以把｛（B-42000）M1-12×C1-C2｝看成一個常數。因此，所列方程就是一個關于X的一元一次方程。當M2-M1＜0時，此函數為遞減函數；當M2-M1＞0時，此函數為遞增函數；當M2-M1=0時，此函數是一條平行于X軸的直線。

根據個人所得稅稅率表納稅等級劃分，當獎金數額在區間［0，B］由小變大時，M2的值會由小變大，M1的值會由大變小。所以Y值先遞減再遞增一定會存在一個最小值，且這個最小值是在M2≤M1情況下取得的。由于這是一個實際運用問題，獎金的變動引起工資的變動，隨之引起二者對應的稅率變動，在［0，B］這個區間內，要綜合考慮二者的變動將X的取值［0，B］分段，在每段的兩端分別是這一段函數的最大值和最小值。通過分析得知，由于B＞60000，所以在實際工作中只要X能夠取到以下區間：（0，18000］，（18000，54000］，（54000，108000］，（108000，420000］， （420000，660000］， （660000，960000］，（960000，+∞），雖然函數在這些區間內是非連續函數，但是在這些區間的兩端一定分別取得在該區間內的最大值和最小值。因此在實際工作中進行工資和獎金的分配時，根據年收入的多少，分別取這些區間的端點值為獎金數額計算應繳納的個人所得稅，納稅額最少的那一組就是最優組合方案。

現舉一個實例來驗證前面的推導結果。

案例3：假設年收入為200，000元

由于獎金數額的增減會影響到工資數額，而他們所對應的稅率也在隨之變動。因此綜合考慮二者對應稅率的變動，將區間［0，200000］劃分成以下幾個區間進行討論。

①當0≤X≤18000時，獎金對應的稅率M2=3%，工資扣除費用后對應的稅率M1=25%。

Y=12｛［（200000-X）/12-3500］×25%-1005｝+3%×X

=-0.22X+27440

此函數圖像如圖1所示。（圖1）

從圖1可以看出該段函數是一個遞減函數，當X=18000時取的Y的最小值23480。

②當18000＜X＜50000時，獎金對應的稅率M2=10%，工資扣除費用后對應的稅率M1=25%。

Y=12 ｛［（200000-X）/12-3500］×25%-1005｝+（10%×X-105）

=-0.15×X+27335

此函數圖像如圖2所示。（圖2）

從圖2可以看出該段函數是一個遞減函數，當X無限接近50，000時取的Y的最小值19，835。

③當50000≤X≤54000時，獎金對應的稅率M2=10%，工資扣除費用后對應的稅率M1=20%。

Y=12｛［（200000-X）/12-3500］×20%-555｝+（10%×X-105）

=-0.1×X+24835

此函數圖像如圖3所示。（圖3）

從圖3可以看出該段函數是一個遞減函數，當X=54000時取的Y的最小值19，435。

④當54000＜X＜104000時，獎金對應的稅率M2=20%，工資扣除費用后對應的稅率M1=20%。

Y=12｛［（200000-X）/12-3500］×20%-555｝+（20%×X-555）

=24835

從圖4可以看出這段函數是一條線段，Y恒定為24385。（圖 4）

⑤當104000≤X≤108000時，獎金對應的稅率M2=20%，工資扣除費用后對應的稅率M1=10%。

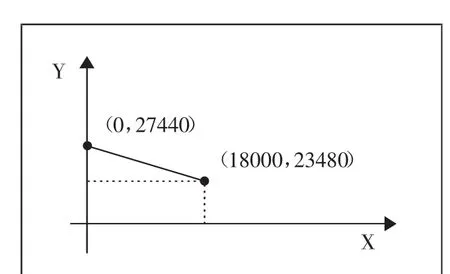
圖1

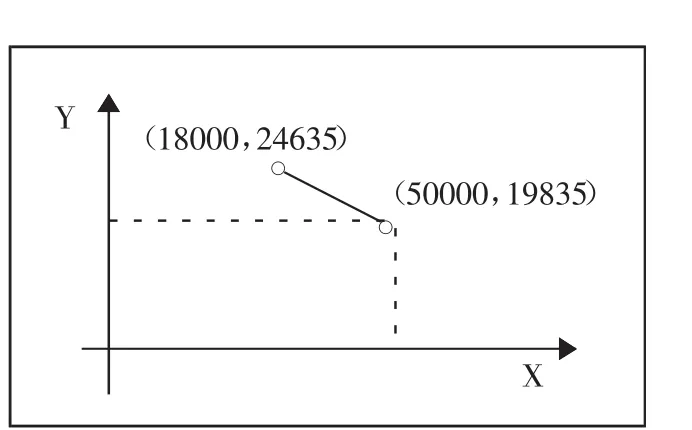
圖2

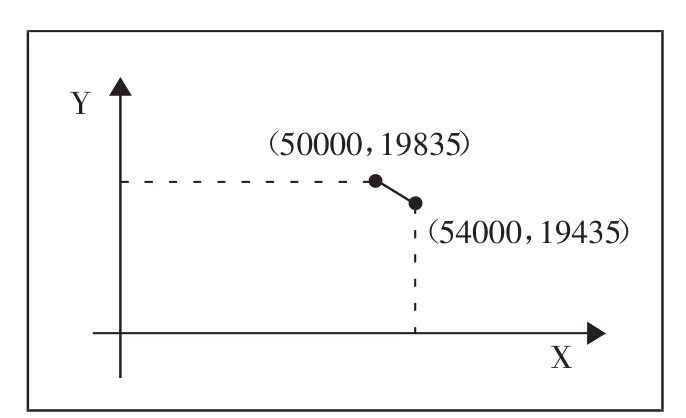
圖3

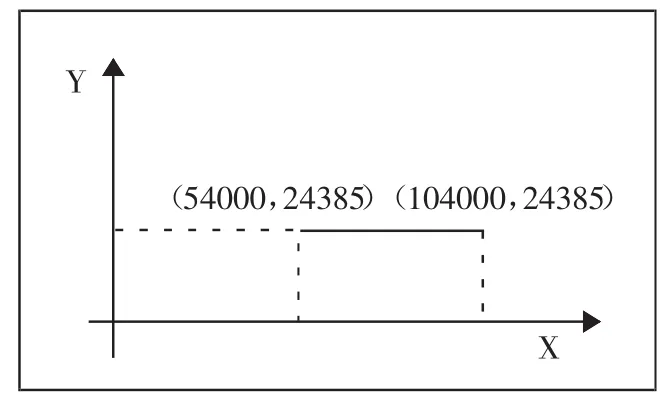
圖4

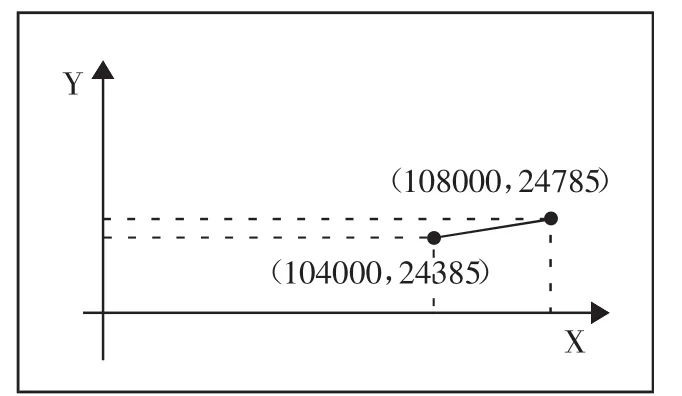
圖5

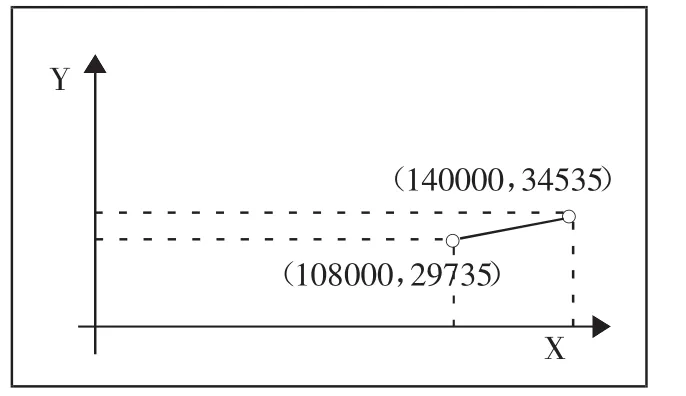
圖6

Y=12｛（200000-X）/12-3500］×10%-105｝+（20%×X-555）

=0.1×X+13985

此函數圖像如圖5所示。（圖5）

從圖5可以看出這段函數是一個遞增函數，當X=104000時取的Y的最小值24，385。

⑥當108000＜X＜140000時，獎金對應的稅率M2=25%，工資扣除費用后對應的稅率M1=10%。

Y=12 ｛［（200000-X）/12-3500］×10%-105｝+（25% ×X-1005）

=0.15×X+13535

此函數圖像如圖6所示。（圖6）

從圖6可以看出這段函數是一個遞增函數，當X無限趨近108000時取得Y的最小值。

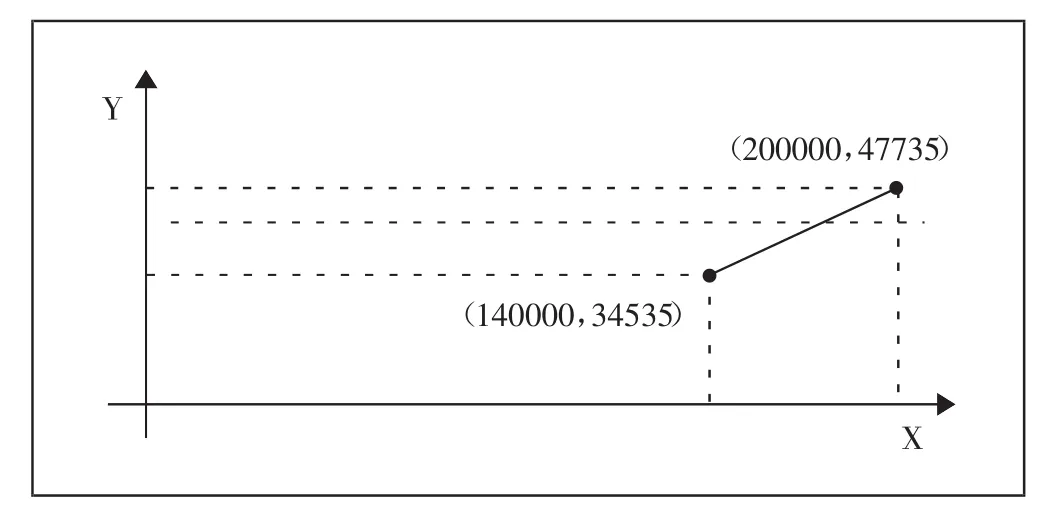
圖7

⑦當140000≤X≤200000時，獎金對應的稅率M2=25%，工資扣除費用后對應的稅率M1=3%。

Y=0.22×X-3735

此函數圖像如圖7所示。（圖7）

從圖7可以看出這段函數是一個遞增函數，當X=140000時取的Y的最小值34，535。

綜合考慮這七個分段函數，得出X=54000時，Y取得最小值19435。當把這些分段函數合起來可以看到，函數在［0，54000］區間是二段不連續遞減函數，在（54000，104000］區間是一段平行于X軸的線段，在［10400，200000］區間是二段不連續遞增函數。在上述三個區間的端點分別取得該函數的最大值和最小值。

這一實例的結果與前面的推導結果相符。所以，根據前面的分析計算筆者總結出一個規則，在年收入一定的情況下，不考慮任何支出以及其他方面的因素，可以確定工資和獎金最優組合。即根據年收入的多少，分別取獎金等于18，000元、54，000 元、108，000 元、420，000 元、660，000 元、960，000 元來計算應繳納的所得稅（需要注意的是：根據前面的分析得知，如果獎金所對應的稅率大于每月工資時，這種組合值屬于遞增函數上的點，一定不是最優組合，因此不用考慮），所得稅最少的那一組所對應的工資與獎金就是最優組合。■