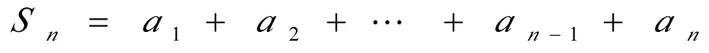例談中職數學中數形結合思想的滲透
——等差數列前項和公式的推導
◆楊 薇
(麗水市職業高級中學)
例談中職數學中數形結合思想的滲透
——等差數列前項和公式的推導
◆楊 薇
(麗水市職業高級中學)
針對中職生數學學習現狀,結合教材,提出數形結合借助圖形,推導等差數列前N項和求和公式以及結合中職學生思維的依賴性,遲緩性,被動性等特點,用數形結合的方法類比面積公式記憶求和公式。通過以形助數培養學生的數形結合思想,激發學習興趣、激勵學習信心。
數形結合 思想方法 中職生 等差數列前N項和公式 應用
數形結合是一種數學研究、數學思考、數學應用的思想方法,其本質就是根據數與形之間的對應關系,通過數與形的相互轉化來解決數學問題,因此數形結合是提高中職學生數形轉化能力和遷移思維能力的非常有效的途徑。
下面以《等差數列前N項和公式推導》教學為例說明數形結合思想如何在教學中進行滲透。
環節一:創設易于“數形結合”的情境
欣賞一段視頻——泰姬陵,泰姬陵是全部用白色大理石建成的宮殿式陵園,傳說她的陵寢中有面大理石墻壁,墻壁上有一個等邊三角形的圖案,用了相同大小的圓寶石鑲嵌而成的(如圖),一共有100層,那么你能計算出這100層一共有多少顆寶石嗎?

創設“數形結合”的情境是激活學生學習的內驅力,從而激發學生的學習熱情,是調動學生積極學習的有效方法。學生對高斯的算法是熟悉的,知道采用“首尾配對”的方法來求和
1+2+3+4+…+100=(1+100)+(2+99)+(3+98)+…+(50+51)=5050
雖然可以求出答案,但是他們對這種“首尾配對”方法的認識僅僅還是處于模仿、記憶的階段,不能靈活的運用。為了促進學生對這種算法的進一步理解,設計了問題一。
環節二:等差數列求和公式的推導
1.問題一:這個全等三角形的圖案中,第1層到第15層一共有多少顆寶石?
這是一個求奇數項和的問題,如果只是簡單的使用“首尾配對”將不能直接給出答案,而要將奇數項問題轉化為偶數項求解,進而引申出一個問題:求若干個前自然數之和是不是需要看其項數的奇偶呢?即求1+2+3+……+n需討論n的奇偶呢?而對于這種需要分類討論的問題中職生們往往望而卻步,不知從何下手,進而引導學生思考是否還有更簡捷的做法?
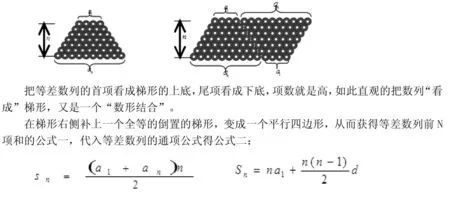
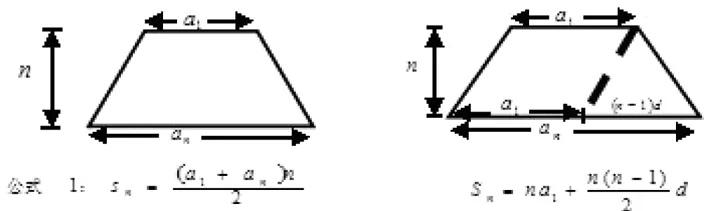
利用多媒體課件的進行直觀演示:把全等的一個三角形倒置,與原圖補成平行四邊形,啟發誘導學生觀察思考。
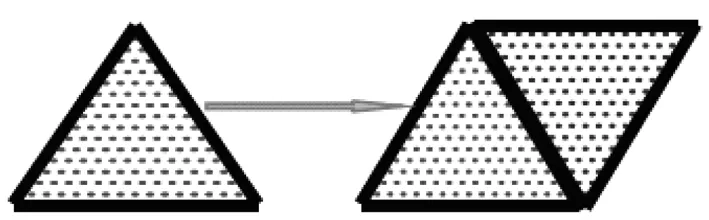
回憶初中學過的三角形面積公式的推導,補上一個全等的三角形就變成了平行四邊形,那每層的個數都相等(1+15=16),共有15層,非常直觀,容易的得出算法。這種借助幾何圖形的直觀特點,引導學生使用熟悉的幾何方法:把“全等三角形”倒置,與原圖補成一個平行四邊形,從而求出答案。這正是數形結合思想方法的最好滲透,具體、直觀,體現的恰到好處。
2.問題二:圖案中從第1層到第n層(1 從求確定具體的的前n個正整數之和到求一般項數的前n個正整數之和,目的在于讓學生領會從特殊到一般的研究方法。 問題三:在公差為d的等差數列中,定義前n項和為,如何求? 聯想到練習題中堆木料的例子,從直觀的圖像出發,把等差數列“看成”一個梯形,引導學生實現從一個數列“配對”的方法發展到兩個數列的“配對”,為“倒序相加方法”做一個鋪墊。 如圖所示: 幾何圖形能非常直觀地啟發學生的推導思路,幫助理解知識,因此作為中職的數學老師在平時的教學中,更要鼓勵學生借助幾何直觀進行思考,滲透了數形結合的數學思想,培養數形結合的學習意識,學會用圖來幫助理解數,真正的學活起來。 本環節從數形結合的角度設計一系列的問題,目的也就是引導學生從“形”出發探究等差數列求和公式,避免了用首尾相加的方法要討論的項數的奇偶問題,更直觀形象的推導出求和公式,也為后面公式的記憶奠定了基礎。 環節三:類比梯形面積公式記憶求和公式,體會數形結合的魅力 教師可做適當的提示引導聯想到將兩個公式與梯形面積公式建立聯系。將求和公式1與梯形面積公式建立聯系,其實初中所學的梯形面積公式的推導也正是利用了倒置的思想。 公式2與梯形面積的另一種推導方法相類比。用“割”的方法,把梯形分割成一個平行四邊形和一個三角形,所求梯形面積就是這兩部分面積之和。 借助圖形的輔助,充分利用圖形直觀形象的特點,類比著記憶數學公式,不僅可以激發中職生的學習興趣,還能更有效地提高學習效率。這種采用形狀記憶法的好處就是圖形和公式互相印證,互相提醒。用這種方法記憶數學公式,學生不僅便于理解,而且記憶特別深刻。同時,有了圖形的介入,學生不需要死記硬背,對公式的理解加深了,學習數學興趣也得到了提高,公式的記憶自然也就更高效了。 環節四:變式練習,進一步滲透數形結合的思想 一個筆架,最下面一層放10支筆,往上每一層都比它下面 一層多放5支,最上面一層放90支.這個筆架上共放著多少支筆? 學生獨立完成變式訓練題,提高了學生將實際問題轉化為等差數列模型的能力,也強化數形結合的意識,滲透等差數列前n項和公式與梯形面積公式結構的類比記憶達到了對求和公式的辨析應用效果,進一步加深了數形結合這一思想方法的印象。 本課例“潤雨細無聲式”的滲透了數形結合的思想方法,使學生對數形結合這一基本數學思想有了更深刻的理解和認識,充分的體會到了數形結合所帶來的魅力。利用數與形的轉換,繞過一些學習障礙,使得許多學生不易理解的問題變得明了了。通過以形助數培養學生的數形結合思想;借助于幾何直觀類比記憶公式,真正掌握公式。 縱觀整個中職數學教學,大部分都是在數形結合的思想指引下展開的,只有靈活、有效的用好數形結合這個工具,才能真正理解、掌握、運用數學知識和數學方法,從而提高學生的數學分析思維能力和解決數學問題的能力,以及學生的邏輯思維能力和形象思維能力。相信長此以往一定能樹立起中等職業學校學生學習數學的信心。 [1]韋中慶.數形結合思想在解題中的應用.中學教學參考,2011. [2]王佳燈.數形結合解題中要注意的幾個問題.數學教學,2005,(5). [3]張宏良.淺談數學教學中的數形結合思想.衡水學院學報,2005,(3):24. [4]康小玲.數形結合法.數學教學通訊,2002,(5):46.