淺談《幾何畫板》在初中數學教學中的應用

沈琦

【摘要】 初中數學教學的最大難點，莫過于函數和幾何這兩大板塊，其概念的抽象以及動態的變化過程，都給教師的教學、學生的學習，帶來了很大的困難.因此，運用信息技術輔助教學，引起了越來越多教師的重視.在眾多的教學軟件中，《幾何畫板》因其圖形編輯方面的優勢，受到許多教師的喜愛.運用《幾何畫板》，能更好地激發學生學習的熱情，切實有效地提高課堂教學的效率.

【關鍵詞】 幾何畫板；初中數學教學；二次函數；變式教學

數學課程標準指出：教師要充分考慮信息技術對數學學習內容和方式的影響，開發并向學生提供豐富的學習資源，把現代信息技術作為學生學習數學和解決問題的有力工具，有效地改進教與學的方式，使學生樂意并有可能投入到現實地、探索性地數學活動中去.就數學學科而言，尤其是幾何以及涉及圖像的函數教學，《幾何畫板》具有不可替代的優越性.下面，筆者結合自己在教學中的例子，談一點體會.

一、利用《幾何畫板》研究二次函數y = ax2及y = a（x + m）2的平移

二次函數的平移，是對數形結合思想的集中體現，傳統的教學方法中，教師會引導學生先將y = ax2及y = a（x + m）2的圖像畫出，然后逐一進行類比，通過觀察它們的異同，尋找其中的變化規律.這種教學方法的弊端是：

① 要作多個函數的圖像，課堂效率較低；且對函數性質的認識受限于圖像是否畫得足夠規范；

② 無法有效地從運動的觀點來揭示問題的本質，學生往往一知半解，容易形成教師的“一言堂”.尤其是對圖像平移“左加右減”這一規律的認識，往往容易與坐標平移“左減右加”相互混淆，教學效果不佳.

利用《幾何畫板》，可以有效解決這些問題，以下是筆者上課的片段：

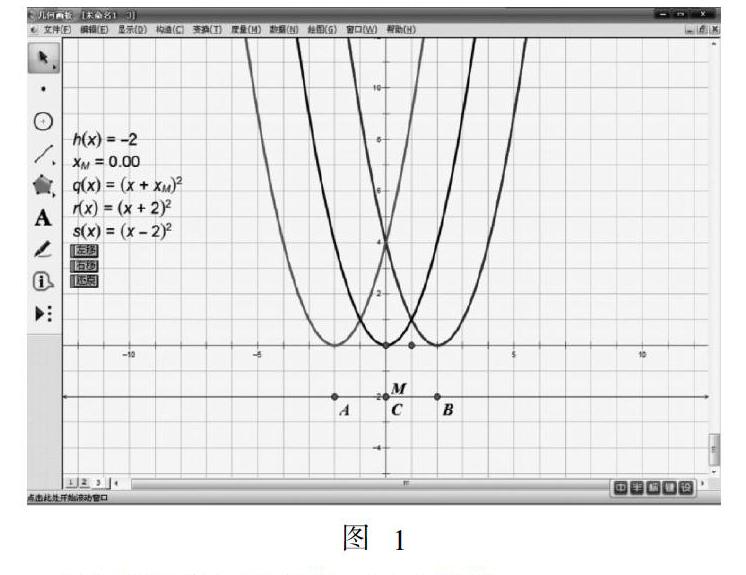
片段1：利用《幾何畫板》研究拋物線y = x2，y=（x + 2）2以及y = （x - 2）2之間的關系.

第一步：利用“繪圖”菜單下的“定義坐標系”功能建立平面直角坐標系，再利用“繪制新函數”功能構造任意直線（如直線y = -2）；

第二步：在平面直角坐標系中繪制以下三點A（-2，-2）、B（2，-2）、C（0，-2），以及在直線y = -2上的任意一點M，度量出點M的橫坐標XM；

第三步：依次在坐標系中，繪制二次函數y = （x + xm）2，y = （x + 2）2以及y = （x - 2）2的圖像；

第四步：依次選中M點和A點，利用“編輯”菜單下“操作類按鈕”構造“移動”按鈕，將其改名為“右移”；依次選中M點和B點，構造“左移”按鈕；選中M點和C點，構造“還原”按鈕.（如圖1）

此時，教師通過對“左移”、“右移”、“還原”三個按鈕的控制，提出以下問題：

師：在平移的過程中，拋物線的什么不變？什么發生了改變？

生1：開口方向不變.

生2：頂點坐標和對稱軸發生了改變.

師：拋物線y = （x + 2）2的頂點坐標和對稱軸分別是什么？

生3：頂點坐標是（-2，0），對稱軸是直線x = -2.

師：拋物線y = x2向哪個方向平移多少個單位，可以得到拋物線y = （x - 2）2？

生：向右平移2個單位.

緊接著，我與學生一起概括了拋物線y = a（x + m）2的性質，以及它與拋物線y = ax2的關系.通過對這一動態過程的觀察，學生很容易地得出m的值對整個平移過程中的影響，直觀明了，易于理解，也就印象深刻.

二、利用《幾何畫板》進行變式教學

初中數學提倡變式教學，教師通常在保持教學內容核心本質不變的前提下，改變其外在的某些屬性，引導學生從不同的角度去換位思考，從而更準確的認識所學知識點的本質和內涵.以圖形教學為例，教師可以從變換問題的條件和結論，或者對圖形作間隔、缺損、重疊、交錯等方式的處理，來達到變式教學的目的.

在傳統的課堂中，教師為了進行變式教學，往往需要耗費許多寶貴的時間來大量地板書作圖，而畫出來的圖形有時不夠準確，又都是靜態的，容易掩蓋一些內在規律，也就很難真正引起學生主動探究的欲望，教學效果大打折扣.

《幾何畫板》作為一種專門研究動態幾何的教學軟件，在這方面有著明顯的優勢.下面是筆者關于《三角形的中位線》一課中的一道課本練習題的教學過程.

片段2：首先，教師利用幾何畫板，出示原題以及相關圖形.（如圖1）

求證：順次連接四邊形四條邊的中點，所得的四邊形是平行四邊形.

并引導學生通過聯結四邊形對角線，利用三角形中位線定理完成證明.

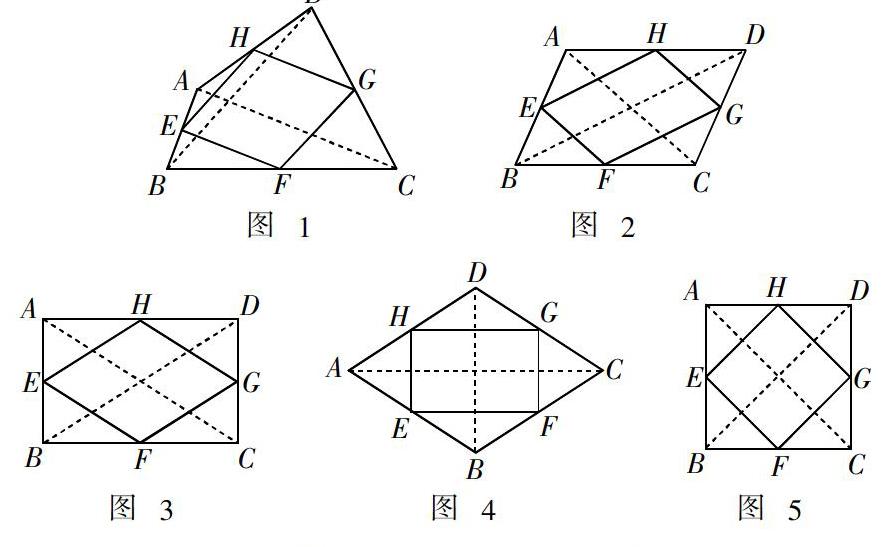
接下來，開始進行變式教學：（如圖2～5）

變式一：若四邊形ABCD是平行四邊形，則四邊形EFGH是什么形狀的圖形？

變式二：若四邊形ABCD是矩形，則四邊形EFGH是什么形狀的圖形？

變式三：若四邊形ABCD是菱形，則四邊形EFGH是什么形狀的圖形？

變式四：若四邊形ABCD是正方形，則四邊形EFGH是什么形狀的圖形？

此時教師進一步提問：四邊形EFGH的形狀與四邊形ABCD的什么因素有關？并運用幾何畫板不斷變換四邊形ABCD的形狀，只保持對角線相等或垂直.從而總結得出：四邊形EFGH的形狀是由四邊形ABCD對角線的關系所決定的.

在這節課的教學過程中，教師事先利用《幾何畫板》制作好教學課件，將問題逐一展示，不斷深入挖掘問題的本質，《幾何畫板》處理信息量大、圖形顯示鮮明準確的優點得到了淋漓盡致的體現.

在以上兩個例子中，充分體現了運用《幾何畫板》輔助教學的兩個優勢：

1. 培養學習興趣，提高教學效率

美國教育家布盧姆早就說過：學習的最大動力，是對學習材料的興趣.有時，總是有些無法入門的感覺，久而久之，還容易產生畏懼心理，究其原因，首先是這部分內容過于抽象，不易理解.其次，在學習方式上，它與其他內容也有很大的不同，一味地埋頭計算是很難學好的.尤其是函數的性質，死記硬背往往容易將幾個函數的性質混淆在一起.事實上，教材在處理函數性質時，知識的建構也始終是圍繞圖形來展開的.在探究函數性質的過程中，需要學生和老師一起，繪制大量的圖形，然而利用黑板的傳統教學中，基本只能處理靜態的函數圖像，無法將運動的過程演示出來.學生在學習時，往往只能依靠自己的抽象思維，一旦無法透徹理解，就只能將老師講的結論強行記住，教學效果自然不佳.通過使用《幾何畫板》，既可以讓教師節省大量的繪圖時間，又能動態的展示函數圖像的形成以及變化過程.教師還可以將幾個函數的圖像事先畫在一個屏幕上，引導學生對這些圖形進行對比和分析，教學效率的提升是顯而易見的.如果條件允許，教師還可以教學生操作《幾何畫板》的基本方法，引導學生自主探究一些課本中的簡單問題.從而更能激發學生學習的熱情，有助于發揮學生的主體性、積極性和創造性.在這個過程中，學生能更深切地認識到，數與形相結合，才是學好函數的最重要的途徑.

2. 深入變式教學，擴大課堂容量

新課改的不斷深入，告訴我們要注重培養學生應變能力，創新能力.而“變式教學”是實現這一目標的有效途徑之一.通過“變式教學”，一題多變，一題多解，使學生對原先陳舊的問題產生一種新鮮感，從而產生濃厚的學習興趣，更好地參與到課堂學習中去.幾何的變式教學中，往往需要對現有的圖形作出各種改變，無論是時間還是空間上，都會加大教師教學的難度.使用《幾何畫板》，教師可以輕易地解決這個難題.教師可以事先利用《幾何畫板》畫好圖形，然后根據教學設計的需要，隨意改變原題的題設和結論，同時改變圖形的結構，而不必重新再畫圖形.在進行問題的小結時，還可以將之前出現的各種情況一并展示給學生，從而使學生對問題本質的把握更加深刻.

華羅庚曾說過：“數缺形時少直觀，形少數時難入微；數形結合百般好，隔離分家萬事休”.《幾何畫板》在教學中的使用，能有效地將抽象的數學知識形象化，擴大知識的內涵，豐富教師講課的方式，減輕學生學習的困難.利用《幾何畫板》，更能提高學生對學習的興趣，培養學生善于觀察、勤于總結、自主學習、探究問題的習慣.當然，作為一種輔助教師教學的工具.它也一定有其局限性.事實上，任何教學輔助軟件，都不能取代教師本身在課堂中的作用.一個再好的課件，如果沒有高水平的教師去駕馭它的話，充其量也不過是一個精美的圖形軟件而已，《幾何畫板》當然也無法例外.因此，教師必須處理好兩者之間的平衡關系，在教學中應更加認真地專研教材，仔細備課，真正地做好課件，用好課件，發揮它最大的教學功能.