天線罩和導引頭隔離度對制導系統(tǒng)影響研究

鄭　多, 林德福, 徐興華, 祁載康

(1.北京理工大學宇航學院, 北京 100081; 2. 北京自動化控制設備研究所, 北京 100074)

?

天線罩和導引頭隔離度對制導系統(tǒng)影響研究

鄭多1, 林德福1, 徐興華2, 祁載康1

(1.北京理工大學宇航學院, 北京 100081; 2. 北京自動化控制設備研究所, 北京 100074)

摘要：針對相控陣雷達導引頭的隔離度寄生回路問題,分析了天線罩和導引頭隔離度產(chǎn)生的原因,建立了考慮天線罩和導引頭隔離度的制導系統(tǒng)動力學模型,基于線性時不變系統(tǒng)穩(wěn)定性判據(jù)和無量綱化法研究了天線罩和導引頭隔離度共同作用對制導系統(tǒng)穩(wěn)定工作域的影響。利用無量綱伴隨函數(shù)法研究了天線罩誤差斜率和導引頭隔離度不同疊加情況對脫靶量收斂的影響。研究表明,單一研究天線罩或?qū)б^隔離度所得結(jié)論對導彈制導系統(tǒng)設計缺乏實際指導意義,制導系統(tǒng)穩(wěn)定工作區(qū)域受到天線罩和導引頭隔離度共同作用的影響,二者的疊加情況不同,對制導系統(tǒng)的穩(wěn)定工作區(qū)域和脫靶量收斂的影響不同。正反饋疊加將嚴重影響脫靶量收斂和制導系統(tǒng)穩(wěn)定性,應盡量避免。

關(guān)鍵詞：全捷聯(lián)相控陣雷達導引頭; 天線罩和導引頭隔離度; 穩(wěn)定域; 脫靶量

0引言

隨著相控陣雷達技術(shù)在機載雷達上的成功應用,世界軍事強國正在嘗試將該技術(shù)應用在導引頭上以提高導引頭性能[1]。相控陣雷達導引頭具有波束掃描靈活、視場大、跟蹤速度快、抗干擾能力強等優(yōu)點,可大幅提高導彈的整體技戰(zhàn)術(shù)指標[2]。相控陣雷達導引頭采用全捷聯(lián)安裝方式,使用相控陣天線組代替?zhèn)鹘y(tǒng)的雷達天線和機械結(jié)構(gòu),利用與彈體固聯(lián)的相控陣雷達探測器和陀螺儀的測量信息進行數(shù)學平臺解耦得到制導信號。然而刻度尺系數(shù)誤差、動力學差異和信息處理延遲都會產(chǎn)生導引頭隔離度問題,與天線罩誤差斜率引起的隔離度問題共同作用,嚴重影響制導系統(tǒng)性能。

關(guān)于天線罩的隔離度問題Nesline 等[3-4]學者已經(jīng)對天線罩誤差斜率引起的隔離度寄生回路穩(wěn)定性問題進行深入研究,得到了考慮天線罩誤差斜率隔離度寄生回路穩(wěn)定域,并分析了其對制導系統(tǒng)性能的影響。同時比較提出一種天線罩斜率誤差補償方案,該方案可適當減小對升力面的限制。Zarchan等[5]研究了基于抖動濾波技術(shù)的天線罩誤差斜率補償方案。關(guān)于天線罩誤差斜率估計補償方法的研究,同時還有學者Peterson D[6]、Lin J[7]、Tiwari P K[8]、Song T L[9]等。關(guān)于全捷聯(lián)相控陣雷達導引頭隔離度問題,王嘉鑫等[2,10]首先基于時不變理論,研究了全捷聯(lián)相控陣雷達導引頭隔離度寄生回路的穩(wěn)定性問題,分析了隔離度對制導系統(tǒng)參數(shù)和性能的影響。同時基于時變系統(tǒng)的Lyapunov穩(wěn)定性理論研究了全捷聯(lián)導引頭隔離度對比例導引制導系統(tǒng)有限時間穩(wěn)定性的影響,得出隔離度正反饋易使得比例導引系統(tǒng)提前失穩(wěn)的結(jié)論。

經(jīng)過分析可知,目前關(guān)于相控陣雷達導引頭隔離度問題的研究,只針對天線罩誤差斜率和導引頭隔離度之一進行研究,如文獻[2,10]。而相控陣雷達導引頭受到天線罩和導引頭隔離度的共同作用,單一分析天線罩或?qū)б^隔離度的研究結(jié)果缺乏實際指導意義。

本文首先分析了相控陣雷達天線罩和導引頭隔離度產(chǎn)生的原因,建立了含有天線罩和導引頭隔離度寄生回路的比例導引制導系統(tǒng)模型。基于時不變系統(tǒng)理論,研究了含有隔離度計生回路的制導系統(tǒng)穩(wěn)定域,比較天線罩誤差斜率和導引頭隔離度共同作用下穩(wěn)定域的變化情況。最后,研究了天線罩和導引頭隔離度共同作用對制導系統(tǒng)主要參數(shù)的影響,并分析天線罩誤差斜率和導引頭隔離度不同疊加情況對制導系統(tǒng)脫靶量的影響。

1比例導引制導系統(tǒng)動力學模型

1.1天線罩斜率模型

天線罩是雷達導引頭的必備裝置,可以防止導彈在飛行中受到氣流擾動的影響。同時將天線罩做成錐形,減小氣動阻力,優(yōu)化導彈的氣動特性。

由于天線罩形狀和材料的原因,雷達波束穿過天線罩時會產(chǎn)生彎曲或折射,目標從它的真實位置好像被移動到了折射角η處,如圖1所示，造成視線角偏差,進而影響導彈制導控制系統(tǒng)性能。折射角的符號和幅值取決于導引頭與目標連線所穿過的天線罩部分,一般情況下折射角很小(小于1°),但其變化率將改變制導系統(tǒng)內(nèi)部動力學,影響脫靶量的收斂情況,甚至導致制導控制系統(tǒng)穩(wěn)定性的問題[3]。

圖1　天線罩折射下雷達天線測量關(guān)系

可知,天線罩長細比越大,利于導彈氣動特性,而此時天線罩導致的彈目視線的偏差角增大,不利于制導系統(tǒng)工作,設計時需折中選擇。天線罩誤差斜率模型可以使用以下經(jīng)驗公式[3]進行估計:

(1)

式中,FR為天線罩長細比,FR=LRadome/dRadome,因而要在氣動性能、隱身性能和電磁性能之間做折中選擇;ds為拋物面天線罩直徑(略小于天線罩直徑);ε為天線罩材料介電常數(shù),ε由材料決定,并且隨溫度變化;B為設計頻率偏差;λ為信號波長;km為品質(zhì)因數(shù),表示制造工藝的好壞,其值高表示天線罩的研磨成型好;RT為天線罩瞄準誤差斜率最大期望擺動值的90%。

天線罩的設計工程需在導彈的氣動特性和制導系統(tǒng)影響之間進行折中考慮,天線罩誤差斜率R與總的天線罩斜率擺動值RT有關(guān),故可以取R=±0.5RT,由于復雜工作環(huán)境的影響,使得天線罩斜率誤差是時變的,R=±0.5RT表示取天線罩誤差斜率變化的最大值,圖2給出了RT的變化曲線。

圖2　天線罩斜率變化曲線

由圖2可知,天線罩斜率隨天線罩長細比的增大而線性增大,設計頻率B的偏差將會改變天線罩斜率隨天線罩長細比的變化速率。根據(jù)圖2可以計算天線罩誤差斜率的最大偏差,例如假設設計頻率偏差B=5%,雷達天線波長λ=30.48 mm,天線罩拋物面直徑ds=26.52 cm,設計天線罩長細比FR=3,則RTds/λ=0.8,計算可得RT=0.92,所以天線罩誤差斜率最大偏差為R=±0.046,可根據(jù)計算的最大天線罩誤差斜率對制導系統(tǒng)設計提供指標約束,對導彈的總體設計具有參考價值。

1.2導引頭隔離度模型

根據(jù)彈目幾何關(guān)系,相控陣雷達導引頭角度測量關(guān)系如圖3所示。

圖3　相控陣雷達導引頭穩(wěn)定跟蹤狀態(tài)幾何關(guān)系

圖3中，q為慣性系下真實目標彈目視線角;qs為慣性系下雷達波束空間指向角;θ為彈體系下彈目視線角;η為天線罩瞄準誤差角。

天線罩瞄準誤差角曲線η=f(θ)的斜率稱為天線罩斜率誤差,故定義天線罩誤差斜率為

(2)

根據(jù)上述定義,當導引頭進入穩(wěn)定跟蹤狀態(tài)時,相控陣雷達導引頭測量角度表達式為

(3)

假設雷達天線輸入輸出成線性關(guān)系,設增益為ks(ks>0),穩(wěn)定跟蹤狀態(tài)下近似有qs≈q,則可得

(4)

相控陣雷達導引頭的解耦表達式為

(5)

式中,?gyro由陀螺儀測量得到,考慮刻度尺系數(shù)誤差的影響可表示為?gyro=kg?M。考慮天線罩和導引頭隔離度的制導系統(tǒng)模型如圖4所示。

圖4　考慮天線罩和導引頭隔離度的制導動力學模型

由圖4可知,基于相控陣雷達導引頭的比例導引制導系統(tǒng)隔離度寄生回路由兩部分組成：一部分由于雷達天線罩誤差斜率的存在,使得彈體姿態(tài)耦合進入制導指令,形成天線罩誤差斜率隔離度寄生回路;另一部分由于刻度尺系數(shù)誤差的存在(kg≠ks),使得彈體姿態(tài)不完全解耦,耦合進入制導指令,形成導引頭隔離度寄生回路。二者產(chǎn)生的機理不同,但均會導致彈體姿態(tài)信息耦合進入制導信息形成隔離度寄生回路,改變導彈制導系統(tǒng)的內(nèi)部動力學,影響制導系統(tǒng)的性能。

2相控陣雷達制導系統(tǒng)穩(wěn)定域影響研究

2.1剩余制導時間對制導系統(tǒng)穩(wěn)定域的影響

為了便于研究,對隔離度進行如下定義：

(6)

圖5　簡化后考慮天線罩和導引頭隔離度的制導系統(tǒng)動力學模型

圖5給出了考慮天線罩和導引頭隔離度的比例導引制導系統(tǒng)動力學模型。使用四階動力學模型等效導引頭濾波器和過載駕駛儀動力學[11],其中Tg為制導系統(tǒng)等效時間常數(shù)，Rd為天線罩誤差斜率和導引頭不完全解耦引起的總隔離度水平。根據(jù)圖5可得隔離度寄生回路傳遞函數(shù)為

(7)

(8)

(9)

令Km=Rd(Vc/Vm)N′,則根據(jù)式(9)可得含有隔離度寄生回路的制導系統(tǒng)的特征方程為

(10)

(11)

采用系數(shù)固定法,分別在tgo/Tg=∞,tgo/Tg=10,tgo/Tg=5處分析制導回路的穩(wěn)定性(其中tgo/Tg=∞時,表示制導回路斷開,研究的穩(wěn)定域為隔離度寄生回路的穩(wěn)定域)。根據(jù)勞斯判據(jù)[12],求得不同tgo/Tg處,制導系統(tǒng)穩(wěn)定的參數(shù)約束條件,如圖6所示。

圖6　不同tgo/Tg處,制導系統(tǒng)穩(wěn)定區(qū)域變化情況

由圖6可知,無論是天線罩誤差斜率,還是導引頭刻度尺系數(shù)誤差引起的隔離度問題,制導系統(tǒng)的穩(wěn)定域都具有類似的特點:①負反饋的穩(wěn)定區(qū)域大于正反饋的穩(wěn)定區(qū)域;②隨著無量綱剩余制導時間的減小,制導系統(tǒng)的正反饋穩(wěn)定區(qū)域變小,對負反饋無影響;③彈體氣動外形、有效導航比和彈目相對速度與導彈速度比以及隔離度水平彼此相互制約,需要從總體的角度進行整體優(yōu)化設計,以滿足導彈制導系統(tǒng)的任務需求。

根據(jù)線性系統(tǒng)穩(wěn)定性約束條件,可求得天線罩誤差斜率和導引頭隔離度分別作用下,不同Tα/Tg時,制導系統(tǒng)臨界穩(wěn)定tgo/Tg隨隔離度變化曲線,如圖7 所示。

圖7　臨界穩(wěn)定tgo/Tg隨隔離度變化曲線

由圖7 可知,無量綱攻角滯后時間常數(shù)Tα/Tg相同時,隨著隔離度的加大,臨界穩(wěn)定tgo/Tg加大,穩(wěn)定區(qū)域越小;正反饋相同隔離度水平時,Tα/Tg增大,臨界穩(wěn)定tgo/Tg越大,穩(wěn)定區(qū)域越小。上述結(jié)果表明,從穩(wěn)定性角度考慮,隨著導彈與目標的不斷接近,tgo/Tg減小,基于隔離度寄生回路(假設tgo/Tg→∞,將制導回路斷開)穩(wěn)定域?qū)Ρ壤龑б茖到y(tǒng)隔離度所提的指標,將會失去實際指導意義。

2.2天線罩誤差斜率和導引頭隔離度共同作用下的制導系統(tǒng)穩(wěn)定域

在導彈的初步設計中,導彈的氣動外形、飛行環(huán)境確定后,則最大的Tα/Tg基本確定,根據(jù)確定的最大Tα/Tg,則可以得到對應的保證比例導引制導系統(tǒng)穩(wěn)定的工作區(qū)域。此處取N′=4,Vc/Vm=1,(Tα/Tg)max=2.50,則該條件下的比例導引制導系統(tǒng)穩(wěn)定工作區(qū)域如圖8所示。

由圖8可知,僅考慮導引頭刻度尺系數(shù)誤差引起的隔離度或天線罩誤差斜率引起的隔離度時,根據(jù)氣動參數(shù)(Tα/Tg)max,可以確定隔離度指標約束,即導引頭隔離度水平需要保證在[(Rs)min,(Rs)max]之內(nèi),天線罩誤差斜率應保證在[Rmin,Rmax]之內(nèi),可保證制導系統(tǒng)穩(wěn)定工作。

實際飛行狀態(tài)下,導引頭刻度尺系數(shù)誤差和天線罩誤差斜率共同作用,影響制導系統(tǒng)性能。由于天線罩誤差斜率和導引頭隔離度的符號不確定性,導致在導彈飛行過程中可能出現(xiàn)最惡劣的情況:天線罩誤差斜率和導引頭隔離度同時出現(xiàn)正反饋或負反饋,可描述為:當ks>0時,kg0,此時天線罩誤差斜率和導引頭隔離度共同作用下引起的總隔離度為負反饋;當ks>0時,kg>ks且R<0,天線罩誤差斜率和導引頭隔離度共同作用下引起的隔離度為正反饋。以上情況將嚴重加大隔離度寄生回路的反饋增益,增大彈體姿態(tài)信息耦合進入制導回路的比重,造成更加嚴重的隔離度問題。天線罩誤差斜率和導引頭隔離度同時存在,制導系統(tǒng)總隔離度可能變化范圍為

導致制導系統(tǒng)總的隔離度變化區(qū)間加大,使得分別基于天線罩誤差斜率或?qū)б^隔離度對整個制導系統(tǒng)提供的指標約束不能滿足制導系統(tǒng)穩(wěn)定工作,失去實際指導意義。

天線罩誤差斜率和導引頭隔離度共同作用下的制導系統(tǒng)穩(wěn)定域如圖9所示。

圖8　制導系統(tǒng)穩(wěn)定工作區(qū)域

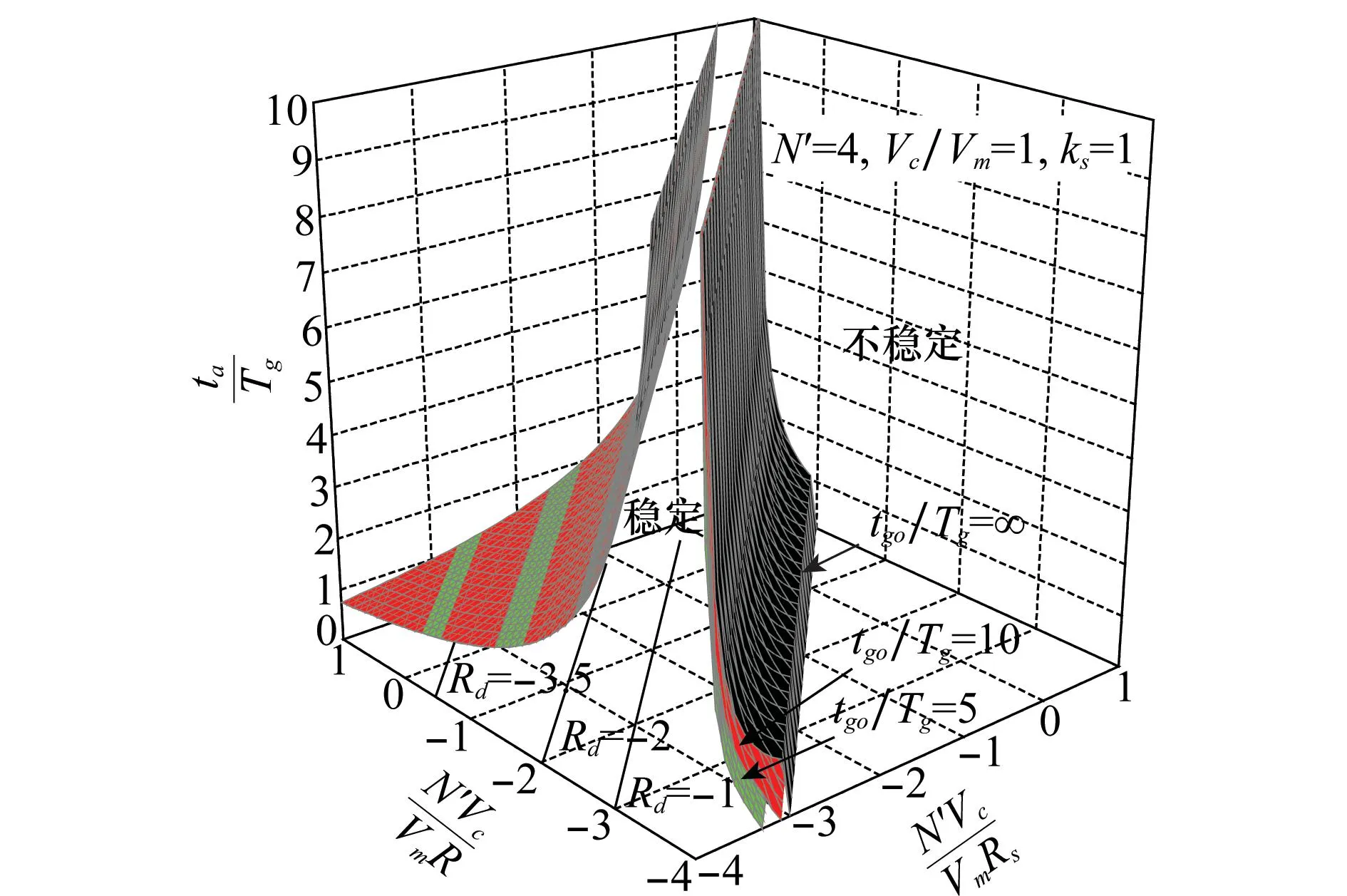
圖9　天線罩誤差斜率和導引頭隔離度共同作用下的制導系統(tǒng)穩(wěn)定域

由圖9可知,導引頭隔離度和天線罩誤差斜率共同作用影響制導系統(tǒng)穩(wěn)定域,且受到無量綱剩余制導時間的影響。當無量綱剩余制導時間tgo/Tg減少時,制導系統(tǒng)穩(wěn)定域減小。天線罩誤差斜率和導引頭隔離度疊加關(guān)系滿足表達式Rd=Rs-ksR,當ks為定值時,天線罩誤差斜率和導引頭隔離度的函數(shù)關(guān)系在其所在平面內(nèi)構(gòu)成直線簇,該直線簇斜率均為ks,而具體位置由Rd確定。當制導系統(tǒng)總隔離度Rd保持不變時,制導系統(tǒng)穩(wěn)定約束下的氣動參數(shù)(Tα/Tg)max不變。當天線罩誤差斜率范圍[Rmin,Rmax]和導引頭隔離度水平[(Rs)min,(Rs)max]確定后,制導系統(tǒng)穩(wěn)定工作區(qū)域基本確定。

3天線罩誤差斜率和導引頭隔離度共同作用對制導系統(tǒng)的影響

3.1對等效制導系統(tǒng)參數(shù)的影響

由于隔離度寄生回路的存在,相當于在制導系統(tǒng)引入了不確定增益的反饋回路,改變了制導系統(tǒng)的內(nèi)部動力學,必然影響制導系統(tǒng)參數(shù),其中最重要的就是對制導時間常數(shù)和有效導航比的影響。

3.1.1對等效制導時間常數(shù)的影響

制導系統(tǒng)等效時間常數(shù)TGEF可以由下式的一次項系數(shù)表示：

(12)

將式(12)無量綱化,等式左右同時除以制導系統(tǒng)時間常數(shù)Tg,得到無量綱等效制導時間常數(shù)

(13)

圖10　無量綱等效制導時間常數(shù)變化曲線

(14)

3.1.2對有效導航比的影響

令s→0時,隔離度寄生回路處于穩(wěn)態(tài),可以求得有效導航比,表達式為

(15)

對式(15)進行尺度變換,等式兩邊同時除以N′,則可以表示為

(16)

由圖11可知,在天線罩誤差斜率和導引頭隔離度共同作用下,天線罩誤差斜率R在±5%內(nèi)變化時,對有效導航比幾乎無影響。有效導航比隨組合參數(shù)N′(Vc/Vm)Rd的增大而增大,隔離度寄生回路正反饋增大有效導航比,隔離度寄生回路負反饋降低有效導航比。

圖11　有效導航比變化曲線

3.2對制導精度的影響

初始速度指向偏差和目標閃爍噪聲是影響雷達體制制導系統(tǒng)精度的主要誤差源,定義初始速度指向偏差角為ε,目標閃爍噪聲的功率譜密度為ΦGN,詳細參數(shù)定義如表1所示。

表1　雷達制導體制典型干擾源參數(shù)定義

根據(jù)如上定義,建立典型干擾情況下相控陣雷達導引頭比例導引制導系統(tǒng)無量綱伴隨模型,如圖12所示。

圖12　典型干擾作用下的比例導引制導系統(tǒng)伴隨模型

根據(jù)上述分析可知,相控陣雷達導引頭制導系統(tǒng)的隔離度問題受到天線罩誤差斜率和導引頭隔離度共同影響,由于導彈在飛行過程中二者變化的不確定性,導致最后制導系統(tǒng)總的隔離度不同。取N′=4,Tα/Tg=3,天線罩誤差斜率為±5%和導引頭隔離度為±3%可保證隔離度寄生回路不失穩(wěn),假設ks=1,則二者不同疊加情況見表2。

根據(jù)圖12建立的無量綱伴隨模型,可以求得不同疊加情況下初始速度指向偏差和目標閃爍噪聲引起的脫靶量收斂情況,如圖13所示。

表2　天線罩誤差斜率和導引頭隔離度疊加情況　%

圖13　不同疊加情況無量綱脫靶量曲線

由圖13可知,天線罩誤差斜率和導引頭隔離度不同疊加情況將影響初始速度指向偏差和目標閃爍噪聲引起的脫靶量的收斂。工程上最不希望,也是最嚴重的情況為圖13中情況3所示,天線罩誤差斜率和導引頭隔離度構(gòu)成的隔離度寄生回路均是正反饋,此時疊加將進一步增大正反饋增益,導致隔離度寄生回路失穩(wěn),脫靶量發(fā)散。

取無量綱末制導時間tF/Tg=10,制導系統(tǒng)參數(shù)取N′=4,Vc/Vm=1,ks=1,通過無量綱伴隨法可求得在不同天線罩誤差斜率情況下,制導系統(tǒng)典型干擾引起的脫靶量隨導引頭隔離度的變化關(guān)系,如圖14所示。

由圖14可知,在天線罩誤差斜率和導引頭隔離度共同作用下,當雷達天線增益系數(shù)ks和天線罩誤差斜率R保持不變時,初始速度指向偏差和目標閃爍噪聲引起的脫靶量隨著導引頭隔離度的加大而增大;導引頭隔離度保持不變,脫靶量隨天線罩誤差斜率的增大而減小。天線罩誤差斜率和導引頭隔離度保持不變時,無量綱攻角滯后時間常數(shù)Tα/Tg越大,脫靶量越容易發(fā)散。同時可知脫靶量受到導引頭隔離度負反饋的影響較小,而對導引頭隔離度正反饋更加敏感。

圖14　天線罩影響下,無量綱脫靶量隨導引頭隔離度變化曲線

根據(jù)上述結(jié)論可知,天線罩誤差斜率和導引頭隔離度共同作用下,二者構(gòu)成的隔離度寄生回路同號反饋疊加情況,正反饋對制導系統(tǒng)的影響遠大于負反饋。故在實際工程應用中,將天線罩和相控陣雷達導引頭一體化設計,可考慮適當主動改變角速度陀螺的刻度尺系數(shù)kg,以使得在天線罩和相控陣雷達導引頭隔離度共同作用下,使其較大概率地出現(xiàn)隔離度負反饋,降低二者共同作用對制導系統(tǒng)的影響。同時將天線罩和導引頭進行整體標定,以最低程度地減小隔離度天線罩誤差斜率和導引頭隔離度的共同作用對制導系統(tǒng)的影響。

4結(jié)論

本文首先分析了全捷聯(lián)相控陣雷達導引頭的制導系統(tǒng)天線罩誤差斜率和導引頭隔離度產(chǎn)生寄生回路的原因,建立了在天線罩和導引頭隔離度共同作用下的比例導引制導系統(tǒng)模型,研究了無量綱制導剩余時間、天線罩和導引頭隔離度對比例導引制導系統(tǒng)穩(wěn)定性影響,并分析了單一研究天線罩或?qū)б^隔離度所得結(jié)論的局限性。根據(jù)所建模型,求得天線罩誤差斜率和導引頭隔離度共同作用下的制導系統(tǒng)穩(wěn)定域。最后,采用無量綱伴隨法,研究了相控陣雷達導引頭典型干擾作用下,天線罩誤差斜率和導引頭隔離度不同疊加情況對制導系統(tǒng)脫靶量收斂的影響。通過研究分析,可得出以下結(jié)論:

(1) 全捷聯(lián)相控陣雷達導引頭受到天線罩誤差斜率和導引頭隔離度的共同影響,制導系統(tǒng)的總隔離度水平為二者隔離度的疊加,基于天線罩誤差斜率或?qū)б^隔離度提出的指標約束無法保證制導系統(tǒng)穩(wěn)定工作,需要考慮二者疊加情況確定制導系統(tǒng)穩(wěn)定域。

(2) 隨著無量綱制導剩余時間tgo/Tg的減小,比例導引制導系統(tǒng)的正反饋穩(wěn)定域?qū)p小,負反饋不受影響。此時基于tgo/Tg=∞的假設(將制導回路斷開,只研究隔離度寄生回路的穩(wěn)定性)求解的穩(wěn)定域?qū)⒉辉贊M足穩(wěn)定性要求。天線罩誤差斜率和導引頭隔離度共同作用下,制導系統(tǒng)的總隔離度體現(xiàn)為二者的疊加,對氣動參數(shù)Tα/Tg設計、打擊目標的彈目接近速度和導彈速度比要求更加嚴格。

(3) 天線罩誤差斜率和導引頭隔離度共同作用下,將改變制導系統(tǒng)內(nèi)部動力學,影響制導系統(tǒng)參數(shù)。等效制導時間常數(shù)的靈敏度受到相控陣雷達導引頭天線增益的影響,將會導致天線罩誤差斜率和導引頭隔離度疊加的權(quán)重不同。天線罩誤差斜率和導引頭隔離度疊加情況的不同,對制導系統(tǒng)脫靶量收斂的影響也不同,最嚴重的情況為同號正反饋疊加,將使得脫靶量迅速發(fā)散。

參考文獻：

[1] Fan H T,Yang J,Zhu X P. Research on beam stabilization technology of phased array radar seeker[J].ActaAeronauticaetAstronauticaSinica,2013,34(2):387-392.(樊會濤,楊軍,朱學平.相控陣雷達導引頭波束穩(wěn)定技術(shù)研究[J].航空學報,2013,34(2):387-392.)

[2] Wang J X,Lin D F,Qi Z K,et al. Study on disturbance rejection rate parasitical loop of strapdown phased array radar seeker[J].TransactionsofBeijingInstituteofTechnology，2013,33(11):1124-1129.(王嘉鑫,林德福,祁載康,等.全捷聯(lián)相控陣雷達導引頭隔離度寄生回路研究[J].北京理工大學學報,2013,33(11): 1124-1129.)

[3] Nesline F W,Zarchan P. Radome induced miss distance in aerodynamically controlled homing missile[C]∥Proc.oftheAIAAGuidance,NavigationandControlConference,1984:99-115.

[4] Nesline F W,Nesline M L. Wing size vs radome compensation in aerodynamically controlled radar homing missiles[J].JournalofGuidance,Control,andDynamics,1986,9(6): 645-649.

[5] Zarchan P,Gratt H. Adaptive radome compensation using dither[J].JournalofGuidance,Control,andDynamics,1999,22(1):51-57.

[6] Peterson D,Otto J,Douglas K. Radome boresight error and compensation techniques for electronically scanned arrays[C]∥Proc.ofthe2ndAnnualAIAASDIOInterceptorTechnologyConference,1993.

[7] Lin J,Chau Y. Radome slope compensation using multiple-model Kalman filters[J].JournalofGuidance,Control,andDyna-mics,1995,18(3): 637-640.

[8] Tiwari P K,Vora P,Bhattacharjee R N. In flight radome error compensation through simulated test data[C]∥Proc.oftheAIAAGuidance,Navigation,andControlConferenceandExhibit，2005.

[9] Song T L,Lee D G,Shin S J. Active homing performance enhancement with multiple model radome slope estimation[J].ProceedingsoftheInstitutionofMechanicalEngineers,PartG:JournalofAerospaceEngineering,2005,219(3): 217-224.

[10] Wang J X,Lin D F,Qi Z K,et al. Effect of strapdown seeker disturbance rejection rate on stability of PNG system[J].InfraredandLaserEngineering, 2013(10): 2608-2613. (王嘉鑫,林德福,祁載康,等.全捷聯(lián)導引頭隔離度對制導穩(wěn)定性的影響[J].紅外與激光工程,2013(10): 2608-2613.)

[11] Zarchan P.Tacticalandstrategicmissileguidance[M].Virginia:American Institute of Aeronautics Astronautics,2007.

[12] Dorf R C, Bishop R H.Moderncontrolsystems[M]. 11th ed. Pearson Education,1995.

鄭多(1987-),男,博士研究生,主要研究方向為飛行器總體設計,導航、制導與控制技術(shù)。

E-mail:zhengduohello@126.com

林德福(1971-),男,教授,博士研究生導師,博士，主要研究方向為飛行器總體設計,無人飛行器自主導航、制導與控制技術(shù)。

E-mail: lindf@bit.edu.cn

徐興華(1989-),女,助理工程師,碩士研究生,主要研究方向為飛行器自主導航技術(shù)。

E-mail: xuxinghua_bit@163.com

祁載康(1936-),男,教授,博士研究生導師,主要研究方向為飛行器總體設計,導航、制導與控制技術(shù)。

E-mail: qzk@bit.edu.cn

網(wǎng)絡優(yōu)先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20141120.2111.010.html

Effect of radome and seeker disturbance rejection rate

parasitic loop on guidance system

ZHENG Duo1, LIN De-fu1, XU Xing-hua2, QI Zai-kang1

(1.SchoolofAerospaceEngineering,BeijingInstituteofTechnology,Beijing100081,China;

2.BeijingInstituteofAutomaticControlEquipment,Beijing100074,China)

Abstract:Aimming at the problem of the disturbance rejection rate parasitic loop of the strapdown phased array radar seeker in practical engineering applications, the causes of the radome and seeker disturbance rejection rate parasitic loop are analyzed, the guidance system model which considers the disturbance rejection rate parasitic of the radome and the seeker is established, the effect of the radome and seeker disturbance rejection rate parasitic loop on the gui-dance system stability region is studied. Based on the dimensionless adjoint function method, the effect of superposition of the radome and seeker disturbance rejection rate parasitic loop on the convergence of miss distance is studied. Researches show that singly studing the disturbance rejection rate parasitic loop of the radome or the seeker is of less practical engineering significance for the design of the missile guidance system, the staility region of the proportion navigation guidance system is affected by the coactions of the radome and seeker disturbance rejection parasitic loop, the gui-dance system stability region and miss distance are affected by different superposition cases. Miss distance and guidance system stability are seriously affected by positive feedback superposition, which should be avoided.

Keywords:strapdown phased array radar seeker; radome and seeker disturbance rejection rate parasitic loop; stability region; miss distance

作者簡介：

中圖分類號：TJ 765.3

文獻標志碼：A

DOI:10.3969/j.issn.1001-506X.2015.07.20

基金項目：國家自然科學基金(61172182)資助課題

收稿日期：2014-07-11；修回日期：2014-10-30；網(wǎng)絡優(yōu)先出版日期：2014-11-20。