基于專業(yè)模塊的高等數(shù)學(xué)實驗課的設(shè)計研究

班曉倩

摘要：文章結(jié)合財經(jīng)類大學(xué)專業(yè)特點，提出了基于專業(yè)模塊的高等數(shù)學(xué)實驗課的設(shè)計理念，旨在發(fā)揮Matlab軟件優(yōu)勢，激發(fā)學(xué)生學(xué)習(xí)高等數(shù)學(xué)的積極性，提高教學(xué)效率，使數(shù)學(xué)實驗課成為完善課堂教學(xué)的輔助。

關(guān)鍵詞：數(shù)學(xué)實驗；教學(xué)改革；實驗?zāi)K

中圖分類號：G712 文獻(xiàn)標(biāo)志碼：A 文章編號：1674-9324（2016）02-0273-02

為提高學(xué)生的實踐創(chuàng)新能力，高等院校各門課程陸續(xù)開設(shè)了實驗課程，將計算機引進(jìn)了課堂。作為公共基礎(chǔ)課的高等數(shù)學(xué)也納入實驗課的開設(shè)課程。較早進(jìn)入這一領(lǐng)域的是吳贛昌主編了《大學(xué)數(shù)學(xué)立體化教材》系列叢書，這套叢書是應(yīng)用多媒體承載數(shù)學(xué)課堂的一個典范。同時期高等數(shù)學(xué)在財經(jīng)類大學(xué)也開始了數(shù)學(xué)實驗課的嘗試。高等數(shù)學(xué)開設(shè)數(shù)學(xué)實驗課的根本目的是為學(xué)生介紹數(shù)學(xué)軟件Matlab在高等數(shù)學(xué)中的應(yīng)用，介紹與高等數(shù)學(xué)相關(guān)的命令操作，以達(dá)到普及數(shù)學(xué)軟件使用的目的。通過近年不斷探索和嘗試，結(jié)合財經(jīng)大學(xué)人才培養(yǎng)方案，融合教學(xué)改革，總結(jié)部分財經(jīng)大學(xué)開設(shè)實驗課的經(jīng)驗案例。

一、財經(jīng)大學(xué)開設(shè)數(shù)學(xué)實驗課的定位

高等數(shù)學(xué)實驗課定位在高等數(shù)學(xué)課堂教學(xué)的輔助。財經(jīng)大學(xué)兼顧理工、經(jīng)濟(jì)管理兩個模塊，培養(yǎng)目標(biāo)是高素質(zhì)的經(jīng)濟(jì)管理類人才，學(xué)生要具備經(jīng)濟(jì)理論知識，更重要的是掌握學(xué)習(xí)的方法，具備較高動手能力和創(chuàng)新能力，高等數(shù)學(xué)實驗課開設(shè)目標(biāo)與財經(jīng)院校人才培養(yǎng)目標(biāo)一致，在掌握知識點情況下，能發(fā)揮創(chuàng)新性，提出并解決新的問題。學(xué)生學(xué)習(xí)首先是感知教材，再理解教材，為完善教學(xué)環(huán)節(jié)，提高教學(xué)效率和學(xué)生學(xué)習(xí)效率，可以提借助數(shù)學(xué)軟件Matlab的數(shù)值計算以及作圖功能，將抽象的定理直觀化，將定理及性質(zhì)的經(jīng)濟(jì)意義最大程度地直觀地展現(xiàn)在學(xué)生面前，更有利于學(xué)生接受定理，理解定理的經(jīng)濟(jì)意義。

二、基于模塊的高等數(shù)學(xué)實驗設(shè)計理念

在數(shù)學(xué)實驗設(shè)計環(huán)節(jié)。數(shù)學(xué)實驗課承載了雙重任務(wù)，一是介紹數(shù)學(xué)軟件的使用，教會學(xué)生會初步使用數(shù)學(xué)軟件解決高等數(shù)學(xué)問題，二是課堂教學(xué)的有益補充，數(shù)學(xué)實驗課為完善教學(xué)效果、完整教學(xué)課堂起到關(guān)鍵作用，在實驗設(shè)計上凸顯專業(yè)模塊的特點。鑒于此，提出基于模塊的高等數(shù)學(xué)實驗設(shè)計理念，目的是將高等數(shù)學(xué)數(shù)學(xué)實驗設(shè)計與專業(yè)模塊結(jié)合，設(shè)計出專業(yè)特點的數(shù)學(xué)實驗。在設(shè)計實驗時，教師可遵循以下方式，經(jīng)濟(jì)管理類實驗由基礎(chǔ)實驗+經(jīng)濟(jì)管理類體驗實驗構(gòu)成，理工類實驗由基礎(chǔ)實驗+理工類體驗實驗構(gòu)成。

在數(shù)學(xué)實驗課的實施環(huán)節(jié)。首先，由于數(shù)學(xué)實驗課課時有限，為提高教生雙方實驗課效率，編寫一本MATLAB軟件相關(guān)命令的使用手冊，發(fā)給每一位學(xué)生，學(xué)生沒有背命令的后顧之憂，就可以把重心放于鍛煉動手能力，嘗試解決新問題。其次，與單一的講授命令不同，教師結(jié)合課程要求，選擇3～5個基礎(chǔ)實驗進(jìn)行講解和演示，加深學(xué)生對命令使用的掌握，另一方面通過對體驗實驗的演示，加強對課本知識意義的直觀理解。這樣做的優(yōu)勢在于，借助數(shù)學(xué)軟件的特點，彌補課堂教學(xué)在作圖等直觀方面的遺憾，并且能夠讓學(xué)生直觀地看待定理的經(jīng)濟(jì)意義。最后，是學(xué)生通過討論完成實習(xí)作業(yè)的環(huán)節(jié)。教師每節(jié)課預(yù)留出20分鐘完成實習(xí)作業(yè)，并且成為這個環(huán)節(jié)的監(jiān)控者，既觀察學(xué)生的反饋情況，同時更及時有效地解決學(xué)生操作過程中遇到的問題。在這一環(huán)節(jié)中，教師要鼓勵學(xué)生討論，激發(fā)學(xué)生的參與意識。

在高等數(shù)學(xué)實驗課的考核環(huán)節(jié)。教師可以通過多媒體監(jiān)控系統(tǒng)觀察每位學(xué)生的練習(xí)情況，給出一個初步分?jǐn)?shù)。進(jìn)一步，參與學(xué)生練習(xí)、討論情況給出修正分?jǐn)?shù)，最后由實驗報告完成情況給出高等數(shù)學(xué)實驗課的成績。數(shù)學(xué)實驗的實驗報告可以不拘于形式。鼓勵學(xué)生分組完成實驗報告，自選完成2～3道實驗問題。題目可以選擇高等數(shù)學(xué)教材上的問題，鼓勵學(xué)生可以自編問題。

三、以導(dǎo)數(shù)知識點為例，設(shè)計實驗案例

1.基礎(chǔ)實驗：函數(shù)的導(dǎo)數(shù)和微分。

例1 已知函數(shù)y=x·sin3x，求■■，dyx=πΔx=0.1

Matlab程序：

syms x y h %定義變量

h=0.1 %自變量改變量h

y=x*sin（3*x） %輸入函數(shù)

dy=diff（y，x，1） %調(diào)用Matlab函數(shù)diff完成求導(dǎo)

k=subs（dy，x，pi） %調(diào)用Matlab函數(shù)subs完成求導(dǎo)

數(shù)值

ywf=k*h %用微分公式求出微分值

2.經(jīng)管體驗實驗：邊際函數(shù)的經(jīng)濟(jì)意義。

例2 設(shè)巧克力糖每周的需求量q是關(guān)于價格p的函數(shù)q=■。求當(dāng)p=10元時，巧克力糖的邊際需求量，并說明其經(jīng)濟(jì)意義。

Matlab程序：

syms q p h

h=[-5：0.1：10]； %價格差h取為[0，10]區(qū)間的

任意實數(shù)

q=1000/（2*p+1）^2 %需求價格函數(shù)

dq=diff（q，p） %邊際需求函數(shù)

qbj=subs（dq，p，10） %當(dāng)價格p=10元時的邊際需

求

q1=subs（q，p，10）； %當(dāng)價格p=10元時的需求量

q2=subs（q，p，10+h）； %當(dāng)價格p=10+h元時的需

求量

qzs=q2-q1 %qzs為需求量改變量

qwf=qbj*h； %qwf為價格改變量h下的微

分

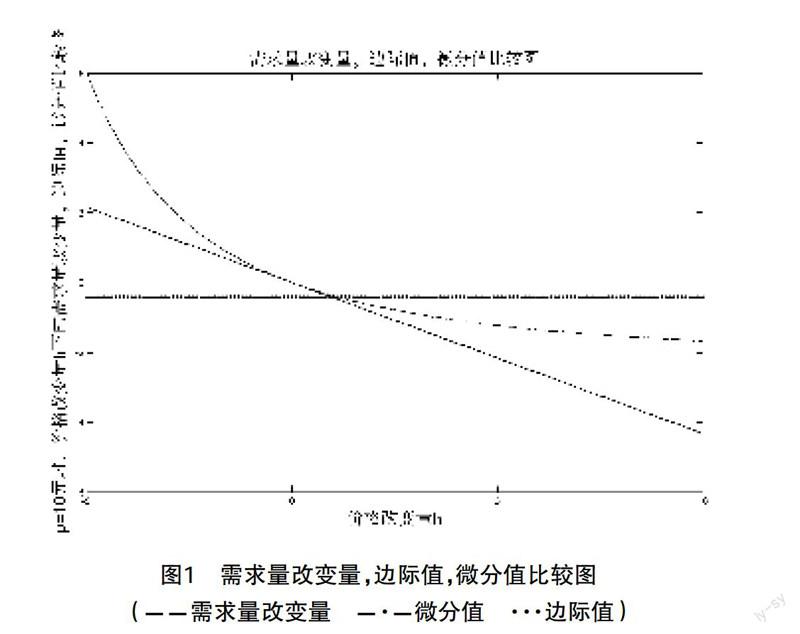
plot（h，qzs，'--'，h，qbj，'*'，h，qwf，'-'） %plot函數(shù)作出需求量改變量，邊際需求，微分值的圖像

結(jié)果和圖形顯示如下：

dq=-4000/（2*p+1）^3

qbj=-0.4319

通過圖示學(xué)生可以觀察到，在價格改變量h=1附近，邊際值與需求量改變量非常接近，所以容易理解邊際值的經(jīng)濟(jì)意義，當(dāng)價格改變一個單位時，邊際值近似等于需求量改變量。同時觀察到，隨著價格改變量的減小或增大，即|h|→0或|h|→∞時，邊際值與需求量改變量差距越來越大，而微分值與需求改變量的差距小于邊際值與需求改變量的差距，所以當(dāng)價格改變量|h|→0或|h|→∞時時，微分近似等于需求量改變量，這就是微分的經(jīng)濟(jì)意義。

四、基于專業(yè)模塊的高等數(shù)學(xué)實驗設(shè)計的意義

實驗課不是教師滿堂灌程序命令，基于模塊的高等數(shù)學(xué)實驗理念圍繞學(xué)生的專業(yè)特點，將定理的意義，通過設(shè)計實驗成為直觀的表象，既演示了數(shù)學(xué)軟件的操作，又讓學(xué)生觀察到定理的意義，給高等數(shù)學(xué)課課程教學(xué)帶來了活力。其次，學(xué)生在教師的指導(dǎo)下進(jìn)行討論和實驗作業(yè)，可增強學(xué)生的參與意識，激發(fā)其探索和創(chuàng)造精神，有助于培養(yǎng)學(xué)生合作能力和解決實際問題的能力，為學(xué)生培養(yǎng)創(chuàng)新能力打基礎(chǔ)。最后，基于模塊的高等數(shù)學(xué)實驗設(shè)計，其案例設(shè)計濃縮了發(fā)現(xiàn)—解決問題的過程，隨著視角的不同，教師可以設(shè)計出不同的體驗案例，這對學(xué)生是一種積極的導(dǎo)向和信號，能激發(fā)學(xué)生勇敢探索，體驗到學(xué)習(xí)的進(jìn)步和發(fā)現(xiàn)的樂趣。

參考文獻(xiàn)：

[1]吳贛昌，等.微積分[M].北京：中國人民大學(xué)出版社，2006，4.

[2]丁衛(wèi)平，李新平.基于數(shù)學(xué)實驗的高等數(shù)學(xué)教學(xué)改革[J].高等理科教，2007，（02）.