一種新的多傳感器群內(nèi)目標精細跟蹤算法

(海軍航空工程學院信息融合研究所,山東煙臺264001)

0 引言

在現(xiàn)實環(huán)境中,經(jīng)常因為不可控制或特定人為目的等因素,會在一個較小的空域分布范圍內(nèi)構(gòu)成一個復雜的目標群,如空間碎片的分裂、彈道導彈突防過程中伴隨的大量碎片及誘餌、掠海飛行的導彈和飛機群等,這些目標空域分布范圍較小,運動特征差異不明顯,相對運動速度較低且特性接近。目標跟蹤領(lǐng)域?qū)⒋祟惸繕朔Q為群目標[1-5]。

在一些實際應用中,與群的整體態(tài)勢相比,往往更關(guān)心群內(nèi)個體目標的情況[3-4]。例如,航天器在軌爆炸后所產(chǎn)生的空間碎片會形成一個群目標,這個群目標將會嚴重威脅太空安全,為消除太空安全隱患,必須精確掌握每一個碎片的運動軌跡,簡單跟蹤群整體已無法滿足工程實際需求;再如,當面對敵方群飛機突防時,為更好地進行戰(zhàn)術(shù)攔截和打擊,要求在探測系統(tǒng)只能部分分辨飛機群的條件下,盡可能精確地估計出群中飛機的個數(shù)及各架飛機的運動軌跡,以便為后續(xù)的作戰(zhàn)決策提供精確的信息支持。此時,為改善跟蹤效果,工程上通常利用多套不同的設備、從不同測向獲取群目標測量數(shù)據(jù),進行數(shù)據(jù)互聯(lián)和融合等處理,多傳感器探測下群內(nèi)目標的精細跟蹤成為必須解決的問題。

但傳統(tǒng)的多目標跟蹤算法[6-15]難以有效跟蹤非機動群內(nèi)目標,因為與傳統(tǒng)多目標相比,雜波環(huán)境下群內(nèi)目標的回波特性明顯復雜,傳統(tǒng)跟蹤算法對群目標回波復雜性考慮不足,漏跟、錯跟、多跟現(xiàn)象嚴重。此外,現(xiàn)有群目標跟蹤算法[16-24]大多基于群整體進行跟蹤,未考慮群內(nèi)目標的精細跟蹤問題;而小部分考慮群內(nèi)目標航跡維持的算法跟蹤環(huán)境又相對單一,難以工程應用。

因此,為解決該問題,本文深入分析群內(nèi)目標回波特性,提出了一種基于形狀方位描述符[25]的集中式多傳感器群內(nèi)目標精細跟蹤(Centralized Multi-Sensor Refined Tracking within Group Targets Based on Shape and Azimuth Descriptor,CMSRT-GT-SAD)算法,并建立了多種典型的仿真環(huán)境,驗證了本文算法的有效性。

1 系統(tǒng)描述

集中式多傳感器群內(nèi)目標跟蹤問題是在雜波中用NS個傳感器上報到融合中心的量測實現(xiàn)群內(nèi)每個目標的狀態(tài)更新。設系統(tǒng)的動態(tài)方程為

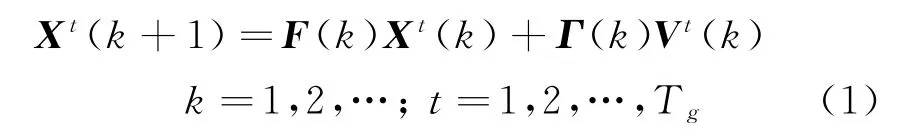
式中:X t(k+1)∈R n為k+1時刻目標的全局狀態(tài)向量;F(k)∈R n為狀態(tài)轉(zhuǎn)移矩陣;T g為第g個群中的目標個數(shù);Γ(k)∈R n,h為噪聲分布矩陣;V t(k)為離散時間白噪聲序列,且E[V t(k)]=0,E[V t(k)V t(k)T]=Q t(k)。

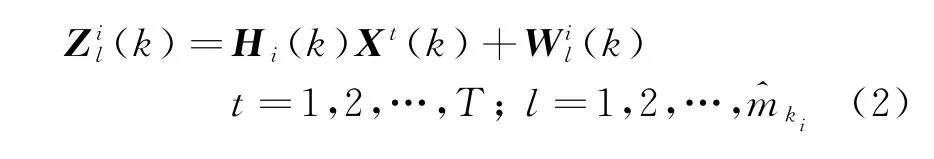
并假定各傳感器間的量測誤差是統(tǒng)計獨立的。

2 CMSRT-GT-SAD算法

2.1 群目標形狀矢量的建立

由群目標的定義可知,在非機動模式下相鄰時刻群內(nèi)目標真實回波構(gòu)成的圖形相似。基于這一原理,可以利用形狀方位描述符[25]分別表示出群內(nèi)各目標狀態(tài)更新值和可能關(guān)聯(lián)量測構(gòu)成的圖形。

形狀方位描述符是數(shù)字圖像處理中描述空間圖形的一種常用方法,由圖像方位框的高度、寬度、面積、比率,以及圖像約束框的高度、寬度、面積、比率、最大半徑、最小半徑、最小半徑角、最大半徑角共12個分量組成[25]。

假設G t(k-1)為k-1時刻第t個群目標,群中包含4個目標,圖1中的圖形A為G t(k-1)的形狀示意圖,t1,t2,t3,t4為群內(nèi)各目標的位置。則利用形狀描述符建立A的形狀矢量為

式中:ω1為圖像方位框的高度,圖像方位框為沿圖像行動方向圍繞物體的最小矩陣,如圖2中的矩形B所示;ω2為B的寬度;ω3為B的面積;ω4為B的比率,即B的面積與A的面積之比;ω5為圖像約束框的高度,圖像約束框為沿圖像主軸方位的包圍物體最小的矩形,如圖3中的矩形C所示;ω6為C的寬度;ω7為C的面積;ω8為C的比率,即C的面積與A的面積之比;ω9為最小半徑,即A的重心與A的邊界元素之間的最小距離;ω10為最大半徑,即A的重心與A的邊界元素之間的最大距離;ω11為最小半徑角,即最小半徑向量相對于水平軸線的角度;ω12為最大半徑角,即最大半徑向量相對于水平軸線的角度。

需要注意的是,當處理直線等特殊圖形時,Ωt(k-1)中的有些分量可能無法獲取,此時可去掉這些分量。由上述描述可知,形狀矢量Ωt(k-1)唯一地表示了圖形A,若兩個圖形的圖形矢量相同,則判定這兩個圖形一致。

在每個時刻更新群內(nèi)各目標狀態(tài)矢量的同時,更新各群航跡的形狀矢量;記k-1時刻群航跡t的形狀矢量為…,12。

圖1 群目標G t(k-1)的形狀示意圖

圖2 圖像方位框示意圖

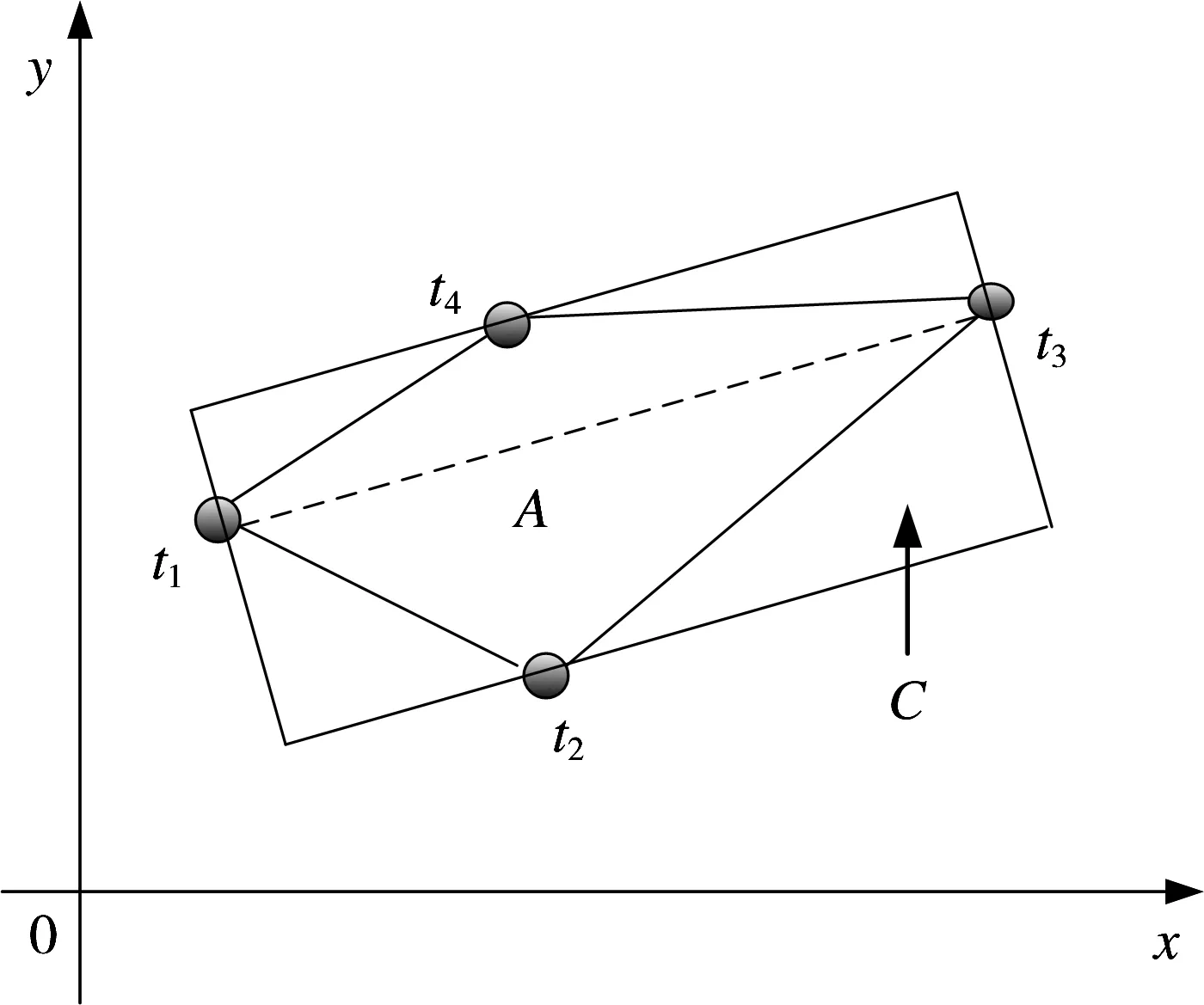
圖3 圖像約束框示意圖

2.2 相似度模型的建立

以G t(k-1)中各目標在k時刻的一步預測值為中心建立關(guān)聯(lián)波門,設Z(k)中落入關(guān)聯(lián)波門的量測集為

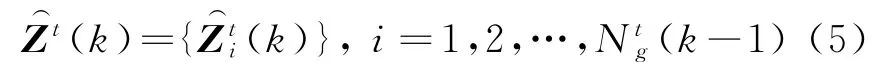
針對傳感器s,基于式(7)建立矢量τ:

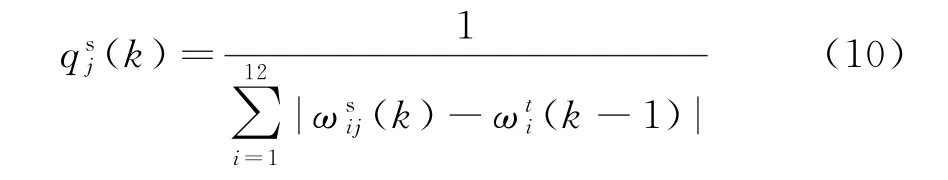
基于式(10),構(gòu)建相似度集合Qs(k)=越大,說明為真的概率越大。為便于比較說明,需要進行歸一化處理,在此定義ρsj(k)為

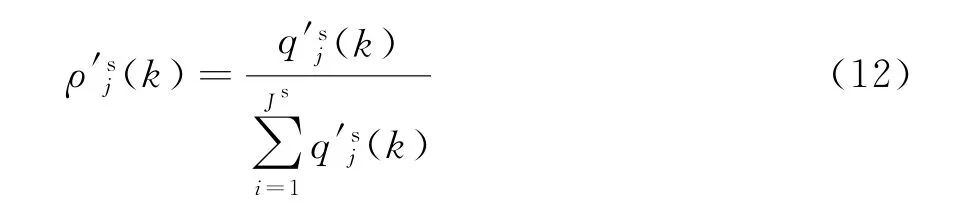
式中,

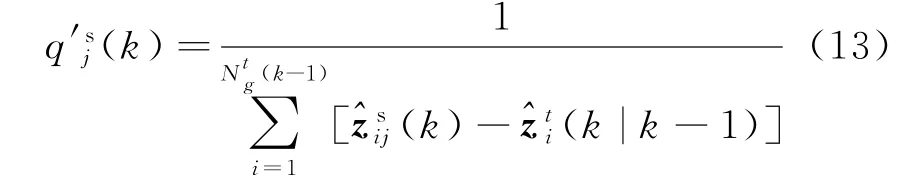
2.3 冗余圖像的剔除

當利用多傳感器對群目標進行探測時,可以獲得對應同一群目標的多幅圖像,所以需要進行冗余圖像的剔除,在此基于選主站的思想解決該問題。

表示選擇傳感器s?為主站,并利用傳感器s?上報的量測集對G t(k-1)進行狀態(tài)更新。

2.4 基于粒子濾波的狀態(tài)更新

3 仿真驗證與分析

為驗證說明算法的性能和有效性,設定兩種典型的群目標運動情況,從算法跟蹤精度、實時性、有效跟蹤率三個方面分析算法的跟蹤性能,并與傳統(tǒng)多傳感器多目標跟蹤算法中性能優(yōu)越的基于數(shù)據(jù)壓縮的集中式多傳感器多假設(數(shù)據(jù)壓縮CMS-MHT)算法[9]進行比較。

3.1 仿真環(huán)境

假定傳感器為3部2D雷達,參數(shù)設置如表1所示。

表1 傳感器參數(shù)設置表

1)環(huán)境1:模擬兩個交叉運動的密集群目標。設在一兩維平面上存在8個目標,構(gòu)成2個群,均作勻速直線運動。前4個目標組成第1個群,各目標的初始位置分別為(5 000 m,800 m),(5 200 m,1 000 m),(5 550 m,1 200 m),(5 700 m,1 400 m),初始速度均為(-200 m/s,300 m/s);第5～8個目標組成第2個群,各目標的初始位置分別為(-5 000 m,8 000 m),(-5 200 m,8 200 m),(-5 550 m,8 400 m),(-5 700 m,8 600 m),初始速度均為(100 m/s,300 m/s)。

仿真中雜波的產(chǎn)生分為兩部分。對普通目標T0而言,以T0為中心在極坐標下建立一個邊長為[10σρ,10σθ]的矩陣,在此矩陣中均勻產(chǎn)生λ1個雜波;對群目標G而言,計算群目標的中心點為中心在極坐標下建立一個邊長為[2ΔGρ+10σρ,2ΔGθ+10σθ]的矩陣(其中ΔGρ,ΔGθ分別為G中各量測在極坐標系兩坐標軸上的最大差值),在此矩陣中均勻產(chǎn)生λ2個雜波。在此,取λ1=2,λ2=4。

2)環(huán)境2:為驗證各算法耗時和有效跟蹤率隨雜波的變化情況,在環(huán)境1的基礎(chǔ)上,雜波的取值如表2所示。

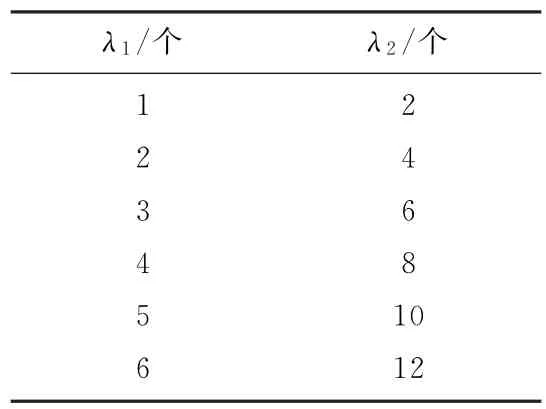
表2 環(huán)境2中雜波取值表

3.2 仿真結(jié)果及分析

圖4為環(huán)境1中群目標真實態(tài)勢圖,從圖中可以看出兩個群目標交叉運動。圖5和圖6分別為環(huán)境1中CMSRT-GT-SAD算法和數(shù)據(jù)壓縮CMS-MHT算法的均方根位置、速度誤差比較圖。從圖中可以看出,本文算法能對目標進行有效跟蹤,均方根位置誤差小于60 m,均方根速度誤差小于2 m/s;而數(shù)據(jù)壓縮CMS-MHT算法的跟蹤效果不理想,在50步以后均方根位置誤差高達300 m以上,均方根速度誤差高達12 m/s以上,在對跟蹤精度要求較高的實際場合中已無法滿足工程要求。

表3為環(huán)境2中各算法有效跟蹤率及算法耗時隨雜波數(shù)變化比較表。從表中可以看出,對應于同樣的雜波數(shù),CMSRT-GT-SAD算法的有效跟蹤率較高,當雜波數(shù)為(6,12)時,有效跟蹤率仍維持在75%以上;數(shù)據(jù)壓縮CMS-MHT算法的有效跟蹤率明顯低于本文算法,當雜波數(shù)為(6,12)時,其有效跟蹤率僅為39.34%,已不能滿足工程需求。此外,隨著雜波數(shù)的增加,兩種算法的有效跟蹤率均有所下降,但數(shù)據(jù)壓縮CMS-MHT算法的下降幅度明顯大于本文算法。

圖4 群目標真實態(tài)勢圖

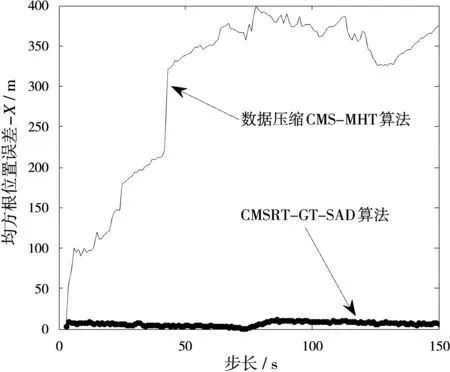
圖5 X方向均方根位置誤差比較圖

圖6 X方向均方根速度誤差比較圖

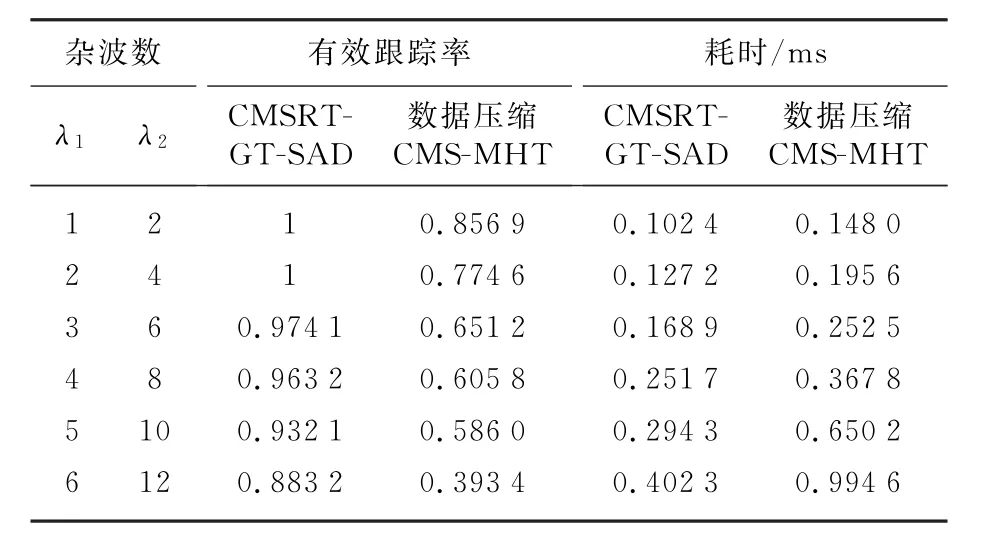
表3 各算法有效跟蹤率及算法耗時隨雜波數(shù)變化比較表

由表3可知,對應同樣的雜波數(shù),CMSRTGT-SAD算法的單次更新耗時小于數(shù)據(jù)壓縮CMS-MHT算法。隨著雜波數(shù)的增加,兩種算法的單次更新耗時均有所增大;但數(shù)據(jù)壓縮CMSMHT算法的增加幅度較大,當雜波數(shù)為(6,12)時,其單次更新耗時已高達0.994 6 ms,在對實時性要求較高的實際場合中已不能滿足工程要求。

4 結(jié)束語

為解決多傳感器群內(nèi)目標的精細跟蹤問題,利用相鄰時刻同一非機動群內(nèi)目標真實回波空間結(jié)構(gòu)相對固定的特性,基于形狀方位描述符,提出了CMSRT-GT-SAD算法。經(jīng)仿真驗證表明,該算法能較好地實現(xiàn)多傳感器探測下非機動群內(nèi)目標的精細跟蹤。

但當群目標發(fā)生整體機動、分裂、合并、分散等機動時,CMSRT-GT-SAD算法將不再適用,因為各探測周期群內(nèi)目標真實回波的空間結(jié)構(gòu)會發(fā)生變化。多傳感器探測下群內(nèi)目標的機動跟蹤是后續(xù)研究的重點和難點。

[1]耿文東.編隊目標跟蹤綜述[C]∥第十屆全國雷達學術(shù)年會,北京:中國電子學會,2008:367-371.

[2]邢鳳勇,熊偉,王海鵬.基于聚類和Hough變換的多編隊航跡起始算法[J].海軍航空工程學院學報,2010,25(6):624-628.

[3]PENG Z H,SUN L,CHEN J,et al.Path Planning of Multiple UAVs Low-Altitude Penetration Based on Improved Multi-Agent Coevolutionary Algorithm[C]∥30th Chinese Control Conference,Yantai:IEEE,2011:4056-4061.

[4]QIN Zhen,SHELTON C R.Improving Multi-Target Tracking via Social Grouping[C]∥25th IEEE Conference on Computer Vision and Pattern Recognition,Providence,Rhode Island:IEEE,2012:1972-1978.

[5]趙盟盟,張群,陳怡君,等.一種用于空間群目標分辨的滑動窗軌跡跟蹤算法[J].宇航學報,2015,36(10):1187-1194.

[6]何友,王國宏,關(guān)欣,等.信息融合理論及應用[M].電子工業(yè)出版社,2010.

[7]TRAN A,MANZANERA A.A Versatile Object Tracking Algorithm Combining Particle Filter and Generalised Hough Transform[C]∥International Conference on Image Processing Theory,Tools and Applications,Orleans,France:IEEE,2015:105-110.[8]ZHOU H,GAO Y,YUAN G,et al.Adaptive Multiple Cues Integration for Particle Filter Tracking[C]∥IET International Radar Conference,Hangzhou:IET,2015:1-6.

[9]張晶煒,熊偉,何友.基于數(shù)據(jù)壓縮的多傳感器多假設算法[J].北京航空航天大學學報,2007,33(12):1448-1451.

[10]JIN Y,DING Y,HAO K,et al.An Endocrine-Based Intelligent Distributed Cooperative Algorithm for Target Tracking in Wireless Sensor Networks[J].Soft Computing,2015,19(5):1427-1441.

[11]陳帥,鄭世友,張世倉.并行多傳感器多目標跟蹤系統(tǒng)性能優(yōu)化算法[J].計算機仿真,2015,32(10):69-73.

[12]陳金廣,江夢茜,馬麗麗,等.具有形狀信息的多傳感器群目標跟蹤算法[J].計算機工程與應用,2015,51(17):210-216.

[13]BEARD M,REUTER S,GRANSTR?M K,et al.Multiple Extended Target Tracking with Labeled Random Finite Sets[J].IEEE Trans on Signal Processing,2016,64(7):1638-1653.

[14]BEARD M,VO B T,VO B N.Bayesian Multi-Target Tracking with Merged Measurements Using Labelled Random Finite Sets[J].IEEE Trans on Signal Processing,2015,63(6):1433-1447.

[15]金亮亮,劉亞云.一種改進自適應機動目標跟蹤算法[J].雷達科學與技術(shù),2014,12(1):97-100.

[16]郭巳秋.粒子群優(yōu)化目標跟蹤方法及技術(shù)[D].北京:北京理工大學,2015.

[17]邵燕生.一種面向圖像信息傳輸?shù)哪繕烁櫵惴ㄑ芯縖J].計算機與數(shù)字工程,2015,43(12):2155-2157.

[18]PANAKKAL V P,VELMURUGAN R.A Factor Graph Approach for Efficient JPDA Implementation in Multi-Target Tracking[C]∥IEEE Aerospace Conference,Bigsky,MT:IEEE,2015:1-15.

[19]PLOPLYS N J,KENEFIC R J.Multiple Hypothesis Tracking Using Maximum Weight Independent Set:US9291708[P].2016-03-22.

[20]KIM C,LI F,CIPTADI A,et al.Multiple Hypothesis Tracking Revisited[C]∥IEEE International Conference on Computer Vision,Santiago,Chile:IEEE,2015:4696-4704.

[21]吳曉雨,吳凌琳,楊磊.基于壓縮感知的粒子濾波跟蹤算法[J].系統(tǒng)工程與電子技術(shù),2015,37(11):2617-2622.

[22]張明杰,康寶生.一種基于圖模型的粒子濾波跟蹤方法[J].計算機應用研究,2016,33(2):590-593.

[23]陳飛.多目標跟蹤的邊緣分布貝葉斯濾波方法研究[D].深圳:深圳大學,2015.

[24]于洪波,王國宏,曹倩.基于聚類的多目標自適應互聯(lián)跟蹤算法[J].中國科學:信息科學,2015,45(8):953-967.

[25]PRATT W K.數(shù)字圖像處理[M].鄧魯華,張延恒,譯.北京:機械工業(yè)出版社,2005.