基于改進PIDNN滑模控制的電壓型PWM整流器

彭一芯　魏建勛　黃輝先　方鑫　陸建龍

摘要：針對傳統(tǒng)滑模變結構控制在三相電壓型PWM整流器中應用時參數(shù)攝動所引起的抖動現(xiàn)象，提出一種改進PID神經(jīng)網(wǎng)絡的滑模變結構在線控制方法，將PID三個參數(shù)作為神經(jīng)網(wǎng)絡隱藏層的神經(jīng)元，利用PID算法響應快、無靜差的特點以及神經(jīng)網(wǎng)絡的在線自學習能力，實時對滑模趨近律參數(shù)進行修改，從而縮短系統(tǒng)狀態(tài)進入滑模面的時間并減小抖動。對選取的價值函數(shù)進行改進，使算法不會陷入局部最優(yōu)而逼近全局最優(yōu)解，并對系統(tǒng)的全局穩(wěn)定性進行分析。通過仿真和實驗驗證，結果表明該方法能使系統(tǒng)全局穩(wěn)定，抖動有明顯削弱且具有更好的動態(tài)響應。

關鍵詞：PWM整流器；滑模變結構；PID神經(jīng)網(wǎng)絡；趨近律；全局最優(yōu)解

中圖分類號：TM46 文獻標識碼：A

1引言

在電力電子技術應用領域中，PWM整流器具有實現(xiàn)能量雙向流動、直流側(cè)電壓恒定、電網(wǎng)諧波低、功率因素可調(diào)等特點，因而得到了廣泛使用。近幾年，針對PI控制器的缺點提出了一種滑模變結構控制（SMVSC）策略，其物理實現(xiàn)簡單，對參數(shù)變化和擾動不靈敏，響應速度快，適用面廣，能夠很好的應用于PWM整流器中，然而滑模變結構控制在本質(zhì)上的不連續(xù)開關特性將會引起系統(tǒng)的抖振，使得穩(wěn)定性降低的同時增加了控制器的運算量。

針對滑模變結構控制中的抖振現(xiàn)象，本文提出了一種改進PID神經(jīng)網(wǎng)絡復合控制（PIDNN）與滑模變結構相結合的控制方案，相比于傳統(tǒng)滑模變結構控制，新的方案具有實時性好，無需精確的數(shù)學模型，魯棒性強，在數(shù)字信號處理器（digital signalprocessor，DSP）上易于實現(xiàn)，能夠很好的減小系統(tǒng)抖振等特點。

2三相電壓型PWM整流器數(shù)學模型

三相電壓型PWM整流器主電路如圖1。圖中e_a、e_b、e_c為相位互差120°的三相交流電壓，i_a、i_b、i_c為三相交流側(cè)電流，R為交流側(cè)等效電阻、L為濾波電感、U_dc為直流側(cè)電壓，i_L為負載電流，R_L為負載電阻，C為負載電容，以及s_a、s_b、s_c為整流器IGBT的開關函數(shù)。

由于三相靜止坐標系下的數(shù)學模型具有非線性時變特性，不利于控制系統(tǒng)的設計。根據(jù)功率不變原則，將三相靜止坐標系下的數(shù)學模型轉(zhuǎn)換到d-q同步旋轉(zhuǎn)坐標系，轉(zhuǎn)換后的數(shù)學模型如下：

式中：e_d、e_q為交流側(cè)電動勢的d、q分量；i_d、i_q為交流側(cè)電流的d、q分量；s_d、s_q為整流橋d-q坐標系下的開關函數(shù)。

3雙閉環(huán)滑模變結構控制算法設計

3.1電壓外環(huán)滑模面的選取與計算單元的設計

滑模變結構控制器設計主要包括兩個環(huán)節(jié)，一是滑模面的選取，其次是趨近律的設計。

在三相VSR雙閉環(huán)控制系統(tǒng)中，內(nèi)環(huán)有功電流i_d是電壓外環(huán)計算所得到的內(nèi)部變量，則在系統(tǒng)滑模面的設計時需要控制的變量為外環(huán)電壓U_dc和內(nèi)環(huán)無功電流i_q。為了使得輸出直流電壓穩(wěn)定在給定值，需滿足等式U_dc=U_dcref。設計如下滑模面：

根據(jù)式（1）將電壓狀態(tài)變量表達式帶入式（2），得：

3.2電流內(nèi)環(huán)無功電流i_q滑模面選取

為了滿足系統(tǒng)在單位功率因素下運行，設計滑模面如下：

3.3趨近律的選擇

為了使系統(tǒng)狀態(tài)更快到達切換面且改善趨近運動的動態(tài)品質(zhì)，本文采用了滿足存在性、可達性和穩(wěn)定性要求的指數(shù)趨近律進行趨近，令：根據(jù)式（1）可得如下狀態(tài)方程：

根據(jù)式（1）、（6）、（7）、（8）、（9）可以得出滑模控制律為：

在指數(shù)趨近律公式中，kS可以保證系統(tǒng)狀態(tài)偏離切換面很遠時，以較快的速度到達滑模面。當S趨近于0時，kS趨近于0，但是由于Lεsgn（S）并不趨近于0，使得S也不趨近于0，而且系統(tǒng)參數(shù)和電力電子開關器件都具有一定的滯后性，造成系統(tǒng)狀態(tài)在滑模面上來回的運動，從而產(chǎn)生顫振的現(xiàn)象。所以對于Lεsgn（S）中系數(shù)e的選擇變得極其重要，若ε選擇太小，會使得系統(tǒng)達到滑模面的速度過慢，若ε選擇太大，則會使得系統(tǒng)出現(xiàn)超調(diào)甚至不穩(wěn)定的現(xiàn)象。

為了解決上述問題，設計了一種改進PID神經(jīng)網(wǎng)絡控制器，實時對趨近律參數(shù)進行調(diào)整，最大限度的減小抖動。

4改進PID神經(jīng)網(wǎng)絡控制器設計

4.1PID神經(jīng)網(wǎng)絡控制系統(tǒng)結構

PID神經(jīng)網(wǎng)絡是一種多層前向神經(jīng)網(wǎng)絡，與一般神經(jīng)網(wǎng)絡的不同點在于隱藏層的選擇上。一般神經(jīng)網(wǎng)絡中神經(jīng)元的輸入一輸出特性都是靜態(tài)的相同的，而PID神經(jīng)網(wǎng)絡的隱藏層由比例元、積分元、微分元組成，將PID控制規(guī)律融入到神經(jīng)網(wǎng)絡中，它具有PID控制器響應快、超調(diào)小、無靜差的特點和神經(jīng)網(wǎng)絡的在線自學習能力，同時也克服了一般神經(jīng)網(wǎng)絡中的許多缺點。由于PIDNN結構簡單，實現(xiàn)較易，采用DSP等芯片進行實現(xiàn)，算法運算量不大，因此可以很好的使用在實際工程應用。PIDNN結構形式如圖2所示。

控制器采用2-3-1的3層BP神經(jīng)網(wǎng)絡，輸入層輸入分別為給定值r（k）和實際測量值y（k）。

輸入層狀態(tài)函數(shù)為：

式中：l、p、q為輸入的最大限制值。

神經(jīng)網(wǎng)絡中權值是由價值函數(shù)進行訓練更新的，若對初始權值選擇不當，很難保證系統(tǒng)的穩(wěn)定性且容易陷入局部最優(yōu)解。針對這個問題，本文選取的價值函數(shù)為李亞普諾夫穩(wěn)定性判據(jù)所要求的S-ke+e=0條件，后面證明了其不存在局部最優(yōu)解問題：

在三相PWM整流器系統(tǒng)的PIDNN控制器中，兩個輸入信號分別為給定信號和實際測量信號，輸出信號為滑模趨近律增益ε。通過不斷的運算，直到E為一個無限趨近于0的正數(shù)時學習訓練結束，此時已滿足系統(tǒng)穩(wěn)定性要求。在算法中將輸入層到中間層的權值設定為定值：[w_1i，w_2i]=[1，-1]，i=1，2，3，即給定信號與實際測量信號的誤差作為中間層神經(jīng)元的輸入，不進行更新，從而減少了整個系統(tǒng)的計算量。中間層到輸出層的權值通過不斷的訓練得到，其訓練公式為：

4.2局部最優(yōu)解問題

在BP神經(jīng)網(wǎng)絡權值更新時，算法最大的問題就是停留在局部最優(yōu)解上。根據(jù)系統(tǒng)不存在局部最優(yōu)解的條件：當一個函數(shù)的二階導數(shù)不隨著變量改變其符號時，說明函數(shù)變量的曲率符號不變，該系統(tǒng)不存在局部最優(yōu)解。根據(jù)所選取的價值函數(shù)（21），可證明其不存在局部最優(yōu)解。

將所選價值函數(shù)對權值求二階偏導數(shù)：

由式（32）可以看出對所選價值函數(shù)求二階偏導數(shù)其符號始終為正，則該函數(shù)不存在局部最優(yōu)解，但由于神經(jīng)網(wǎng)絡是一種啟發(fā)式算法，不能夠得到精確的全局最優(yōu)解值，但是可以逼近于全局最優(yōu)解，則所得到的解為全局最優(yōu)解或次優(yōu)解。

4.3系統(tǒng)穩(wěn)定性分析

使用李亞普諾夫函數(shù)來判斷系統(tǒng)的穩(wěn)定性，這里選取與價值函數(shù)相同的式子來做判斷：

由此可以看出，當學習步長足夠大時，V為負定，此時的系統(tǒng)是穩(wěn)定的。但在實際應用中，當把學習步長取的太大時，對系統(tǒng)的穩(wěn)定性會產(chǎn)生一定的影響。根據(jù)上述分析，可得到三相PWM整流器PIDD-SMVSC控制原理圖如圖3。

5系統(tǒng)仿真結果及分析

利用Matlab/Simulink平臺搭建了三相電壓型PWM整流器的仿真模型，以本文所提出的方法與傳統(tǒng)滑模變結構控制算法進行仿真對比，驗證其算法的有效性和優(yōu)越性。系統(tǒng)仿真主要參數(shù)為：380V/50HZ正弦交流電輸入，700V直流電壓輸出，交流側(cè)電感為4mH，等效阻抗為0.15 Q，直流側(cè)負載電阻為49Q，電容為235μF。為了使得仿真結果和實物實驗時的參數(shù)基本保持一致，選擇開關頻率為12kHz。

改進PID神經(jīng)網(wǎng)絡滑模控制直流電壓輸出波形如圖4（a）所示，傳統(tǒng)滑模控制直流電壓輸出波形如圖5（a）所示。從兩幅圖的對比可以看出，輸出直流電壓波形都幾乎沒有超調(diào)，但傳統(tǒng)滑模變結構控制達到穩(wěn)態(tài)的時間要長，當達到穩(wěn)態(tài)后，傳統(tǒng)滑模控制的電壓值會在給定電壓±6V之間來回抖動，使得輸出直流電壓質(zhì)量不高。由改進PID神經(jīng)網(wǎng)絡滑模控制算法的仿真波形可以看出，在穩(wěn)態(tài)時的抖動只有±0.05V左右，相比傳統(tǒng)滑模控制方法有明顯的削弱，控制效果更好。

為了進一步的驗證改進PID神經(jīng)網(wǎng)絡滑模控制的動態(tài)性能，分別對負載突變和電壓給定值變化的情況進行了仿真實驗。圖6給出了負載突變時的波形，當系統(tǒng)直流電壓穩(wěn)定后，在0.15S時將負載由50%額定值增至100%額定值。由圖可以看出直流輸出電壓經(jīng)過0.003S恢復至穩(wěn)定值且電流平穩(wěn)的過渡到新的穩(wěn)態(tài)值。

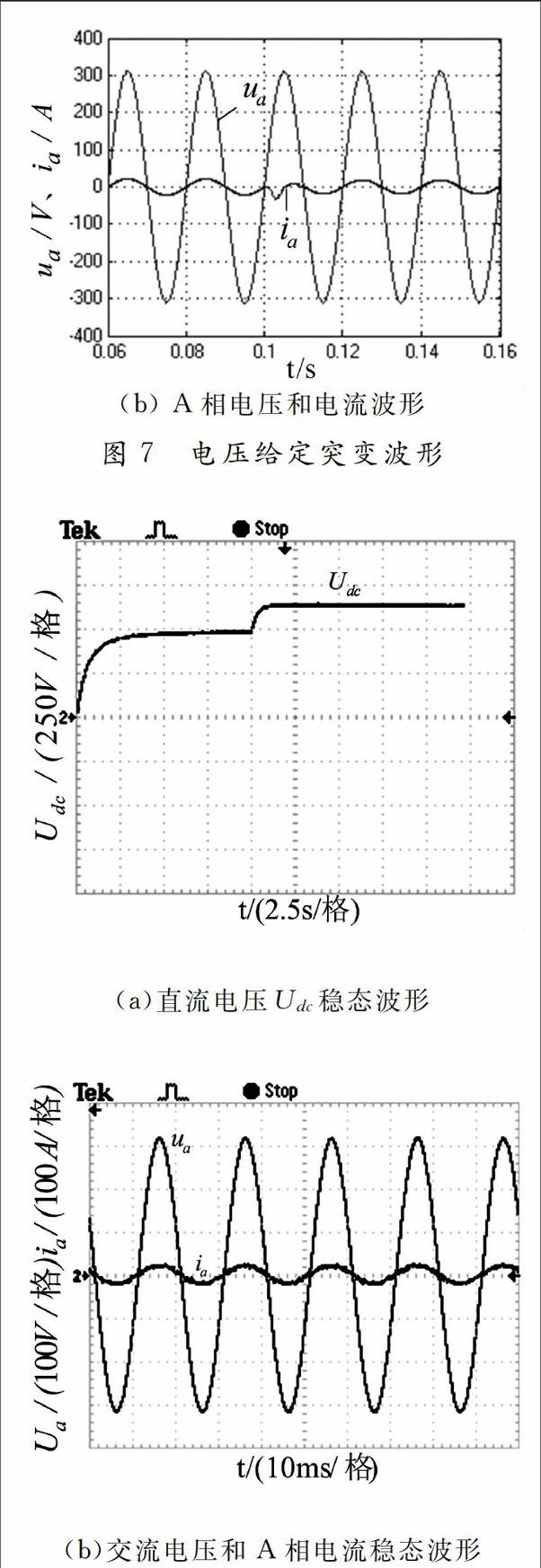
圖7給出了電壓給定突變時的仿真波形，當系統(tǒng)穩(wěn)定后，0.1S時電壓的給定值由700V突變至650V，由圖7（a）仿真波形可以看出經(jīng)過0.01S后到達新的穩(wěn)定狀態(tài)，由圖7（b）可以看出交流電流也很好的過渡到新的穩(wěn)態(tài)，使得電壓突變后同樣保持在單位功率條件下運行。

上述所做的仿真實驗驗證了本文所提出方法的正確性和優(yōu)越性，相比傳統(tǒng)滑模變結構控制能夠更好的消除抖振且具有良好的魯棒性。

6實驗結果

為了驗證仿真結果的正確性，搭建了以TSM320F2818為主控芯片的實驗樣機，主要參數(shù)如下：直流輸出電壓為700V，額定功率為IOKW，IGBT采用三菱公司生產(chǎn)的CMIOODY-24H，交流側(cè)繞線電感為4mH，負載功率電阻為50Ω，負載電容由2個4700μF的電解電容串聯(lián)組成，采用五段式空問矢量技術，其開關頻率為12KHz。圖8（a）為輸出直流電壓波形，由于負載端電容的存在，通電瞬間電容側(cè)相當于短路，從而產(chǎn)生很大的沖擊電流，所以不能直接進行可控整流，而是首先進行帶有軟啟動的不控整流。不控整流10S后直流電壓穩(wěn)定，再由DSP芯片控制進行可控整流。圖8（b）為帶載穩(wěn)態(tài)時的A相電壓電流波形，由圖可以看出，功率因素接近1。圖8（c），（d）分別為帶載和空載時由不控整流到可控整流時直流電壓和交流A相電流波形。圖8（e）為在空載穩(wěn)態(tài)運行后轉(zhuǎn)換為帶載情況下的直流電壓和交流A相電流波形。

7結論

本文在分析了三相電壓型PWM整流器數(shù)學模型的基礎上，針對傳統(tǒng)滑模變結構控制在整流器系統(tǒng)應用時所存在的不足，將改進PID神經(jīng)網(wǎng)絡控制加入到了傳統(tǒng)滑模變結構控制中，使系統(tǒng)不會陷入局部最優(yōu)從而逼近全局最優(yōu)解，利用兩者的優(yōu)點最大幅度的減小了系統(tǒng)的顫振且魯棒性好。由于控制算法簡單，易于在DSP上實現(xiàn)，在搭建的實驗樣機上進行了驗證，取得了很好的控制效果，具有一定的實用價值。