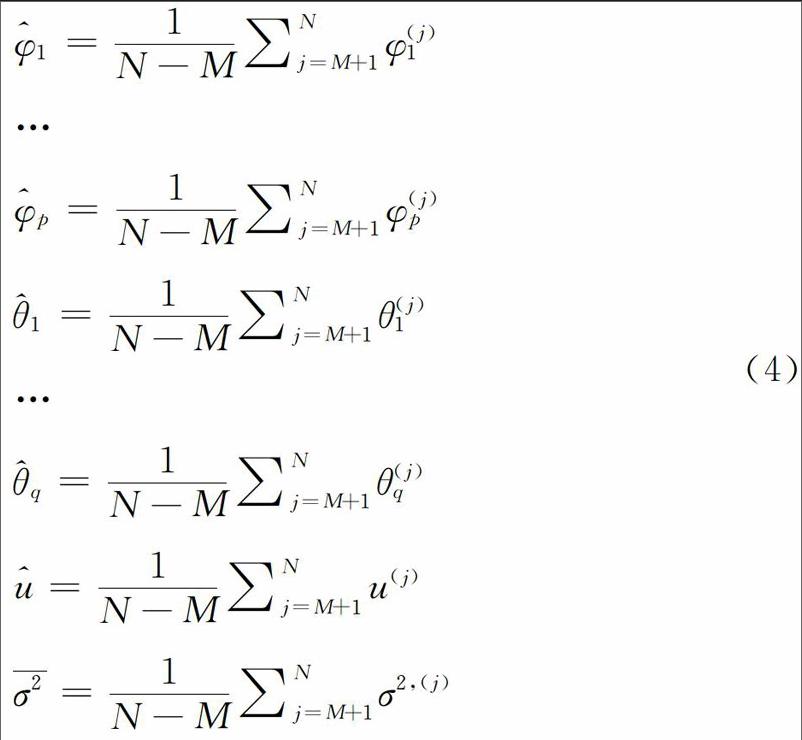湘江流域金屬污染的貝葉斯預測實證研究

劉潭秋　孫湘海

摘要：水環境是一個充滿不確定性的復雜巨系統，傳統水質模型很難體現重金屬污染物在河流中遷移的隨機性。本文選擇ARIMA模型作為重金屬預測模型，運用貝葉斯相關理論進行分析、參數估計和預測，從而不僅獲得點預測結果，而且獲得區間估計和概率預測結果。實例分析證實，基于貝葉斯方法的ARI-MA模型能夠獲得很好的點預測和區間表現。

關鍵詞：時間序列模型；貝葉斯理論；河流重金屬污染；預測

中圖分類號：TP391.9 文獻標識碼：A

1引言

水環境是一個充滿不確定性的復雜巨系統，根據水流流速、污染物的彌散系數、污染物的降解系數與污染物濃度的關系構造的傳統水質模型很難體現重金屬污染物在河流中遷移的隨機性和不確定性。

由Box and Jenkins（1970）提出的自回歸整合移動平均（autoregressivintegratedmoving-aver-age，ARIMA）模型作為最典型的時間序列預測技術，已廣泛應用于各個領域的時序預測研究，水質管理領域亦不例外。此外，貝葉斯統計學作為處理不確定性的一種恰當方法，自上個世紀九十年代起已廣泛被應用于建模。目前，貝葉斯方法廣泛被應用于簡單集總式概念性水文模型的參數和不確定性估計，但很少有研究應用這些方法去估計其他水文模型不確定性，原因是輸入數據和計算時間有限。但是水文研究中，水文建模中的不確定性已經成為一個不可避免的主體。雖然以前只有參數不確定性被關注，但是越來越多的人意識到在建模方法中其它來源不確定性的重要性。

將ARIMA模型與貝葉斯理論相結合，這樣既能夠充分利用ARIMA模型點預測精度較高的優點，又能運用貝葉斯分析和推斷的優勢，實現重金屬污染的概率預測。概率預測不同于點預測，前者不僅能夠給出具體的數值，而且能夠給出出現這個數值結果的可能性（概率），以及在給定的可能性（概率）下，預測結果是什么樣的數值范圍。事實上，自從1969年美國國家氣象局開始制作并發布概率降水預測至今，概率水文預測的概念在國外得到了廣泛的關注，水文學家對此進行了大量的研究，提出了許多方法與模型，極大地豐富了水文預測不確定性研究的理論與實踐，其中貝葉斯預測是一種重要的概率預測方法。

用貝葉斯方法來分析時間序列ARIMA模型，國外己有不少學者做過相關研究，但是將其應用于水質預測，甚或是重金屬污染濃度預測，鮮有人涉足。因此，我們將進行嘗試性研究，這無疑在理論上和實踐上都是一次有益的探索。

2ARIMA模型的貝葉斯推斷

2.1ARIMA模型結構

一個ARIMA（p，o，q）模型的一般表達式為：

其中{X_t}是被研究時間序列，u是常數項，φ_i和θ_i是待估參數，ε_i是隨機誤差項，p和q分別是被研究時間序列和誤差項時間序列的滯后階數且均為正整數。而ARIMA（p，o，q）中“o”表示{X_t}是平穩序列，否則需通過差分處理將其變為平穩序列。

假定被研究變量有T個觀察值，記為X=（X₁，…，X_T）。模型對應的似然函數f（X|ψ）的計算表達式為：

在對模型參數完全未知情況下，可以根據Jeffrey提出的非信息先驗分布設定方法，將模型中參數的先驗分布都被設置為均勻分布，其中模型方差σ²的非信息先驗分布就是f（σ²）∝1/σ²。通常假設模型中各個參數變量是相互獨立的，因此這個聯合先驗密度π（ψ）是各個參數先驗密度的乘積，即π（ψ）=π（φ，θ，u，σ²）=π（φ）·π（θ）·π（u）·π（σ²）∝1/∝，其中-∞<φ，θ，u<-∞，0<σ²<∞。

根據貝葉斯定理，待估參數的后驗密度為：

π（ψ|X）∝f（X|ψ）·π（ψ） （3）

將每個參數的均勻分布式代入上式，就形成模型參數的聯合后驗分布。

在具體的推斷實施過程中，這里采了用Gelf andan dSmith（1990）提出的Gibbs取樣方法，逐一從與各個參數相聯系的滿條件分布取樣。具體步驟為：

6）這樣，就獲得全部參數的第1次完整抽樣，重復上述1）-5）步驟，獲得全部參數的第2次完整抽樣，然后再多次重復上述1）-5）步驟，直至獲得全部參數的第N次完整抽樣。這樣，就形成這個ARIMA模型參數的樣本點序列{φ₁^（j），…，φ_p^（j），θ₁^（j），…，θ_q^（j），μ^（j），σ^2，（j）}_j^N=1。

在實施上述抽樣步驟中，同時監控和檢驗馬爾可夫鏈的收斂，以確保樣本是從平穩分布抽取。目前在實際操作中對于馬爾可夫鏈收斂與否的常用監測方法是樣本圖形分析法、追蹤圖法、自相關圖法，以及一些正式收斂測試法，例如Geweke測試法，Gelman-Rubin測試法等。

2.2ARIMA模型的貝葉斯估計

在完成上述迭代抽樣之后，直接采用如下公式獲得模型參數的均值估計值：

其中，N表示迭代總次數，M表示馬爾可夫鏈收斂前的樣本點。為了避免初始值對最終估計結果的影響，這前M個樣本點必須被拋棄，而這些被拋棄的抽樣迭代部分被稱作燃燒階段。此外，為了保證模型參數貝葉斯估計的準確性，N-M必須是一個足夠大的正整數值，以確保該馬爾可夫鏈收斂。

ARIMA模型的貝葉斯估計，不僅能夠通過4）式獲得模型參數的均值估計值，而且能夠獲得參數其他統計特征值，例如百分位數、標準差等。

2.3ARIMA模型的貝葉斯預測

在貝葉斯方法中，預測是基于所研究變量未來值向量X^F的一個概率分布的構建，并且以過去（被觀察到的）值X向量為條件，并考慮這個預測模型參數ψ的后驗分布。后驗預測密度表達式是：

f（X^F|X）=∫f（X^F|X，ψ）π（ψ|X）dψ （5）

其中f（X^F|X，ψ）是條件預測密度。這個后驗預測密度的MCMC解為：

其中，{ψ^（i）}^Gi=1，是從參數的滿條件分布抽樣獲得，G是馬爾可夫鏈的迭代次數。

這個后驗預測密度f（X^F|X）能夠被解釋為來自條件預測分布f（X^F|X，ψ）的一次平均，權重值是這些參數的后驗概率。貝葉斯預測結果就是預測的可信區間，其反映了所研究現象的不確定性。

3湘江流域重金屬污染的貝葉斯預測實證研究

3.1樣本數據與ARIMA模型的確定

以湘江中下游某個重金屬監測點獲得的一組鎘污染濃度數據為樣本進行實證分析。這組鎘濃度數據是2007-2010年期問每個月固定某個時點鎘在水中濃度的均值，而不是鎘污染濃度隨時間變化的均值，共計40個樣本數據。這些觀測值是等時間間隔連續被記錄的，時間間隔單位是月。選擇前35個樣本數據對神經網絡模型進行訓練，后5個樣本數據則用于與預測結果進行比較，從而驗證模型的預測能力。本次研究所使用的數據與筆者前期開展的使用ARIMA模型來預測重金屬污染濃度研究所使用的數據相同，這樣選擇樣板數據也是便于將本次研究與之前研究工作進行對比。

根據前期研究可知，ARIMA模型的具體表達式為一個ARIMA（1，0，1）模型：

X_t=u+φ₁X_t-1+θ₁ε_t-1+ε_t （7）

其中，X_t表示第t時刻的鎘污染濃度，u是常數項，ε_t是模型殘差項且服從均值為0且方差為常數的學生t分布，φ₁和θ₁是模型需要被估計的參數，這個模型被記為服從學生t分布的ARIMA（1，0，1）模型，或稱為服從學生t分布的ARMA（1，1）模型，建模過程詳見文獻。

3.2模型的貝葉斯分析

基于上述模型的殘差項分布設定，模型的似然函數為：

鑒于本次實證研究對象應用本文所討論方法的相關研究很少，這里采用Jeffrey提出的非信息先驗分布設定方法，在使用傳統ARIMA建模方法獲得參數估計結果基礎上，可將模型的非信息先驗分布設定如下：

π（φ）～Uniform（0，1）

π（θ）～Uniform（-1，0） （9）

π（σ²）～Uniform（0，160）

根據貝葉斯定理，給定數據，模型參數的聯合后驗分布正比于參數聯合先驗分布密度與似然函數的乘積。按照上述對這個ARIMA（1，0，1）模型參數先驗分布的設定，以及顯然這些先驗分布密度相互獨立，因此模型參數的聯合后驗密度就直接正比于模型的似然函數與每個參數先驗密度的乘積，如等式（3）所示。

相應地，參數φ的滿條件分布為：

顯然，這個滿條件分布不服從某個標準的概率統計分布，因此在實施σ²取樣時可采用Metropolis-Hastings算法（參見文獻）。

3.3貝葉斯估計結果

在對所構建的鎘污染濃度預測模型實施完貝葉斯分析后，采用OpenBUGS軟件對模型實施貝葉斯估計。在估計過程中，燃燒期長度選擇為5000次（即，M=5000），觀察自相關圖和追蹤圖可以發現，所有參數的馬爾可夫鏈都很好地收斂了。為了保證估計值的準確性，在燃燒期之后又迭代取樣50000次（即，N=50000）所獲得的樣本點用于（7）式以計算每個參數的馬爾可夫積分，即參數均值估計值。具體結果見表10

3.4貝葉斯預測結果

利用已經完成參數估計的ARIMA（1，0，1）模型來進行預測。首先需要計算預測值的后驗預測密度，根據等式（5），模型的后驗預測密度為

顯然直接對上式積分是很困難的，同樣需要采用MCMC方法來獲得模型的預測結果，即貝葉斯概率預測結果，這樣就很容易預測未來湘江流域鎘污染濃度變化范圍，以及發生可能性，甚至能夠預測極端事件發生的概率。其中貝葉斯均值預測值是通過等式（4）計算得到，其中為了保證馬爾可夫鏈的收斂，G取值了一個相當大的值，即50000。具體預測結果如下一系列表。

由表2可知：貝葉斯概率預測結果表明，在百分位5到百分位95之間所對應的90%可信區間內包含了真實值；貝葉斯概率預測的均值預測結果與ARIMA模型采用傳統建模方法所獲得的點預測結果非常接近真實值，但第二個預測點除外，這也能夠從圖1直觀地感受到。采用常用衡量預測精度的統計量——誤差百分比絕對值均值（MAPE）來進行對比，我們發現貝葉斯均值預測和ARIMA模型的傳統點預測結果所對應的MAPE值分別為0.0542和0.0813，顯然在單個值預測上ARIMA傳統預測方法似乎更優。然而，貝葉斯預測的最大優勢在于其不斷改進的能力，即將實踐經驗不斷融入先驗信息從而不斷改進貝葉斯預測結果，這是傳統ARIMA模型預測所缺乏的。鑒于本研究在應用領域的開創性，因此缺乏相關經驗積累，所以本次貝葉斯預測中所使用的先驗分布采用非信息先驗分布，這是導致這一結果產生的原因。因此，為了進一步改進模型的貝葉斯預測能力，需要在以后的實踐工作中不斷總結預測結果，不斷改進模型參數信息先驗分布的設定，使其不斷逼近真實統計分布。

4結論

將貝葉斯理論和方法與重金屬時間序列預測ARIMA模型相耦合，并對該模型所對應的貝葉斯分析、參數估計和預測理論進行了探討，并在此基礎上實施湘江重金屬污染濃度貝葉斯預測。實例預測結果表明，獲得了較好的均值預測結果和區間預測，而對于現有預測結果的改進有賴于模型參數先驗分布選擇，這需要在預測實踐基礎上不斷改進。