一種LuGre摩擦模型自適應補償的分析及仿真

劉東升　白樺　李文君　宋發興

摘要：介紹一種降低低速轉臺伺服系統在轉動過程中由于摩擦因數影響轉動精度的方法。在低速轉臺轉動的過程中由于摩擦力等的影響，轉臺的速度、位置都會發生偏差，所以在轉臺系統上引入摩擦控制補償。利用公式推理，通過與理論值對比，發現自適應摩擦補償方式與傳統摩擦補償方式相比，其跟蹤誤差大大降低，能有效抑制摩擦干擾對伺服系統的不利影響。進行基于MATLAB環境下的仿真效果。

關鍵詞：摩擦模型；摩擦補償；自適應控制

中圖分類號：TP27 文獻標識碼：A

1引言

轉臺伺服系統低速時的速度精度和速度平穩性是評價轉臺性能好壞的重要標志之一，由于轉臺伺服系統是以經緯度為引導信息，它的位置精度、速度精度和速度平穩性直接影響轉臺所搭載的天線的跟蹤效果，尤其影響轉臺系統的低速性能指標。影響系統低速性能的因素很多，有摩擦力矩，電機波動力矩，測速機的靈敏度，控制系統采樣等。其中最主要的因素是摩擦力矩和電機波動力矩，是摩擦力矩和電機波動力矩造成了轉臺低速運行時的爬行現象、精密定位時的抖動現象以及穩態時有較大的靜差或出現極限環震蕩。由于實際系統都是非線性系統，轉臺在低速運轉時，輸入信號較小，其低速的性能主要取決于非線性因素。其中摩擦力矩是影響性能的主要原因。因此對摩擦力矩進行建模分析，并針對模型進行補償研究，對提高轉臺性能有著重要意義。

2伺服系統的LuGre摩擦模型

在伺服系統中，無論從摩擦現象的角度出發，還是從對其補償的角度出發，對非線性環節建立準確的數學模型，其都是很重要的。已建立的摩擦模型很多，有Karnopp模型、LuGre模型以及綜合模型。其中，LuGre模型是Canudas等在1995年提出的典型伺服系統摩擦模型，此模型對摩擦過程復雜的動態、靜態特性描述準確，如爬行、極限環振蕩、滑前變形、摩擦記憶及靜態Stribeck曲線。此模型描述如下：

對于伺服系統，用式（1）表示：

其中，J為轉動慣量，θ為轉角，μ為控制力矩，F為摩擦力矩。設變量Z代表接觸面鬃毛變形，則F可由下面的LurGre模型來描述：

式中，σ₀、σ₁，稱為動態摩擦參數，F_c、F_s、α、V_s稱為靜態摩擦參數，其中，F_c為庫侖摩擦，F_s為靜摩擦，a為粘性摩擦系數，V_s為切換速度。

2.1基于LurGre摩擦模型的PID控制補償

PID控制是現在自控工程中常用到的一種補償方法，參數易調節，但對于摩擦補償效果不好。我們采用Simulink仿真工具，對PID補償效果進行仿真。仿真圖和模型分別如圖1、圖2所示。

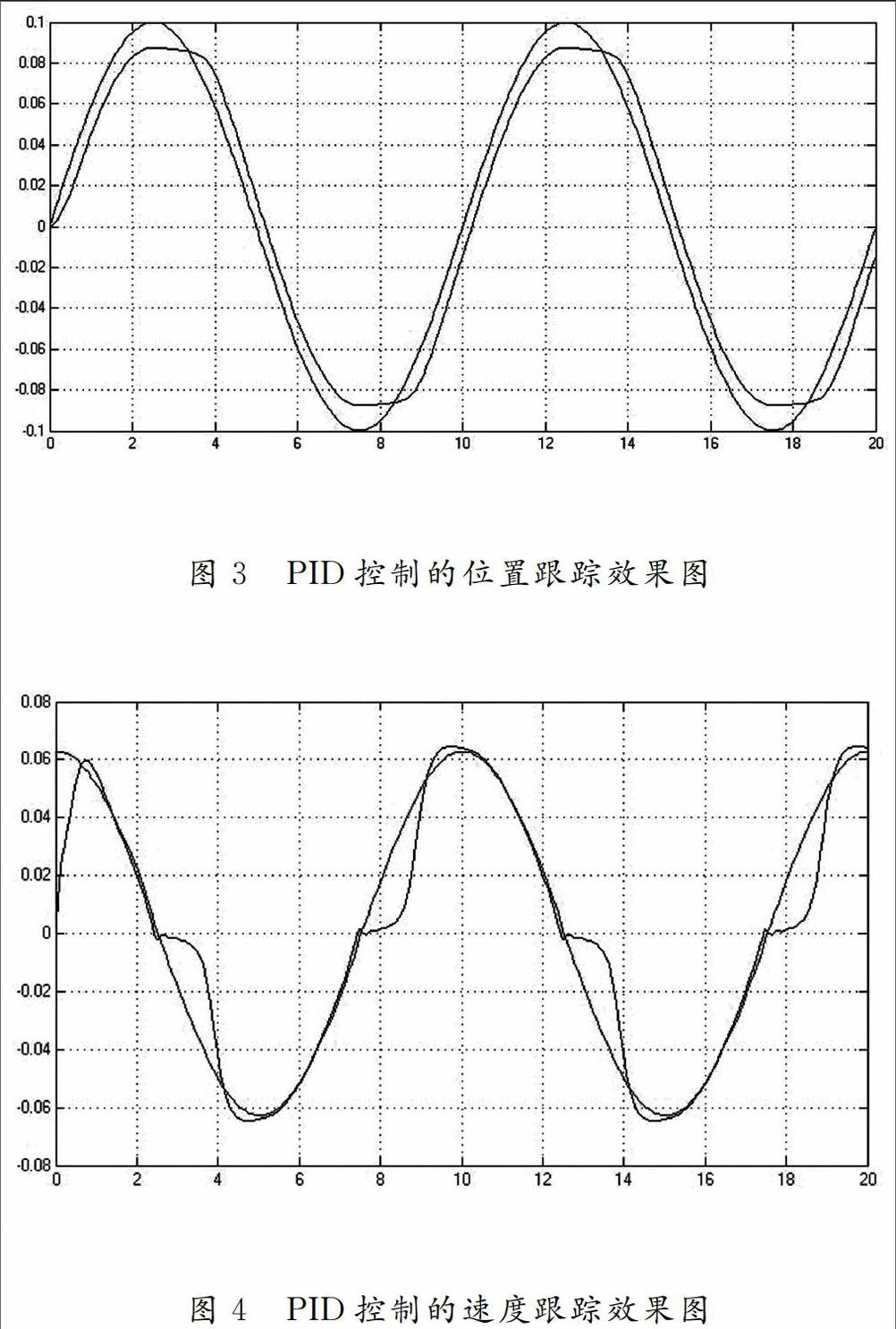
根據伺服系統式（1）及摩擦模型式（2）～式（4），取J=1.0，σ₀-260，σ₁=2.5，α=0.02，F_s=0.34，V_s=0.01。輸入位置指令r（t）=0.1sin（0.2πt）。采用PID控制，取K_p=20，K_d=5.0，仿真時間為20s。其位置和速度跟蹤效果如圖3、圖4所示。

從圖3、圖4的仿真結果看出，在帶摩擦的條件下，采用PID控制對其進行補償，其位置有“平頂”現象，速度跟蹤有“死區”現象，控制的魯棒性較差，不能滿足高精度跟蹤要求。因此必須對LuGre摩擦模型采用更好的補償方法。

2.2基于LuGre摩擦模型的自適應補償

2.2.1基于LuGre摩擦模型的自適應補償設計

由于LuGre模型中有一個不確定的狀態量Z。在實際中，常用觀測器對其觀測，根據觀測結果對伺服系統實現摩擦補償，有助于伺服系統性能的提高。該模型包含LuGre動態模型和自適應控制器，控制器包含參數的自適應律和等效PID控制律，用來估計未知LuGre參數，從而給予補償。最后采用了Lyapunov方法證明，該方法能滿足對期望位置信號的漸近跟蹤。如圖5所示典型電機系統。

由圖5系統模型，可得系統動態方程：

其中σ、σ₀、σ₁是自適應補償參數，自適應補償的重點是設計一個非線性的控制器來補償這些參數的變化。對于位置跟蹤控制，系統誤差方程為：

θ_d（t）為期望位置信號，其兩階可導，k為正值的反饋增益，e₁（t）為位置跟蹤誤差。將式（12）代入式（13）得：

可以看出Lyapunov函數導數是非正函數，可以保證誤差e₂，觀測器誤差z₀、z₁以及未知參數誤差σ、σ₀、σ₀一致有界，由e₁、e₂得知，e₁保證有界，根據期望信號θ_d、θ_ed的定義，可以保證θ_ed、θ、θ一致有界；根據摩擦估計誤差定義，可以得到摩擦狀態Z一致有界，進一步估計，一致有界，從而得到控制規律U₁的有界性。

2.2.2基于LuGre摩擦模型的自適應補償仿真

基于LuGre摩擦模型的自適應補償的simu-link仿真如圖6所示。其中取相關補償參數c=10，β₀=150，β₁=50，β=55。

假定正弦疊加信號，通過自適應補償模型，觀測該信號位置和速度補償效果，結果表明，LuGre摩擦模型的自適應補償在很大程度上減小了摩擦的影響，基本清除了位置跟蹤的“平頂”和速度跟蹤的“死區”現象，從而提高了位置、速度的跟蹤精度。其穩態誤差可控制在1.7*10^-3。左右。位置跟蹤和速度跟蹤效果分別如圖7和圖8所示。

3結束語

在低速轉臺的轉動過程中，由于摩擦因素的影響，必須引入補償系統，給予補償。經過比較分析，得到基于LuGre摩擦模型的自適應補償系統是最適合本低速轉臺伺服系統的，有助于伺服系統性能的提高。最后采用了計算機仿真方法證明，該方法能保證對期望位置信號的漸近跟蹤。合理選擇分析參數，完全可以使跟蹤結果在試驗誤差允許范圍內。