衛星數據加擾方式對OQPSK調制信號的影響分析

江 潔，張風源，陳 劼，林閩佳

（上海航天電子技術研究所，上海 201109）

0 引言

電波主要是在自由空間傳播，信道參數較穩定，信道的主要干擾是加性高斯白噪聲。在此恒參信道中，用相移鍵控（PSK）調制方式可獲得最佳的接收性能，并能有效利用衛星頻帶，因此在現發射機設計中正交相移鍵控（QPSK）調制方式得到了廣泛應用。偏移正交相移鍵控（OQPSK）的實現難度與QPSK相同，但OQPSK的非線性抑制能力更好，目前已成為衛星數據多通道并行下傳方案中的主要調制方式。

OQPSK調制技術已較成熟，相關研究文獻并不多，分析基帶數據流對調制影響則更少。目前，衛星研制中多次出現了傳輸頻譜畸變等現象。與典型調制頻譜相比，畸變頻譜信號主包絡在固定位置出現明顯凹陷，工程中多用增加擾碼長度選取特定碼片臨時解決，未見相關文獻對此現象進行研究。為在工程實踐中更好地使用OQPSK調制技術，本文對基帶數據加擾方式與OQPSK調制頻譜變化進行了研究。

1 衛星數傳信號處理流程

數傳系統主要完成星上各載荷遙感數據的接收、格式化編排、數據復接、加擾、數據存儲、調制、放大、濾波等處理后通過天線下傳信號。數傳鏈路模型如圖1所示，幀格式如圖2所示［1－2］。

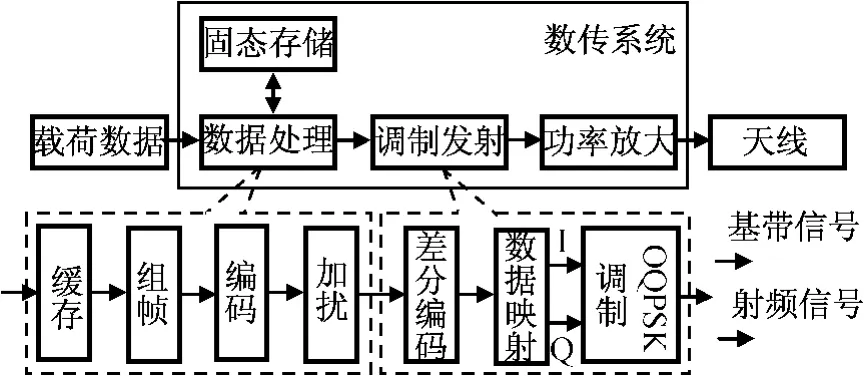
圖1 數傳鏈路模型Fig.1 Model of data transmission chain

載荷數據進入數傳系統后先進行復接和組幀，按圖2中的幀格式要求進行數據編碼處理。數據編碼處理并不改變虛擬信道數據單元（VCDU）數據單元中的數據，只是生成了編碼校驗符。同時，為避免數據出現全“0”、全“1”長碼，數據處理器要求對復接后的數據進行加擾，方法是使數據幀除幀頭外的每位與一個標準的偽隨機序列異或。在接收端，同一序列與所接收的數據幀異或，以去除隨機圖型，恢復原數據。可發現，一旦確定了加擾方式，每幀都會用相同的偽隨機序列序列進行加擾處理。

2 基帶數據流設計

經數據處理后的載荷數據送至調制發射模塊進行OQPSK調制。按現有衛星應用方式進行劃分，數據處理有主要以下兩種。

a）合路加擾

各接口數據關系如圖3所示。

衛星數傳系統中，該組幀方式是一種常見的數據處理方式：載荷數據送入數據處理器后，處理器對數據進行復接和組幀；組幀后的數據以幀為單位進行編碼、加擾；對數據流按bit進行串、并轉換成2路數據分別送至OQPSK調制的I、Q路輸入端。此組幀加擾方式既可保證I、Q每路數據的隨機性，又能保證I、Q兩路數據間關系的隨機性。

b）IQ分路加擾

各接口數據關系如圖4所示。

IQ分路組幀是近年來國內新采用的一種數據處理方式，載荷數據送入數據處理器后，針對調制器的輸入數據流為兩路（I、Q路）的特點，對這兩路數據流分別進行組幀、加擾。其特點是I、Q兩路數據具獨立性，信號解調后，可對其中一路數據直接進行相關分析和使用。此組幀加擾方式可保證I、Q每路數據的隨機性，但由于每幀數據的編碼加擾方式相同，如I、Q兩路間的數據相似或相同，經編碼加擾，兩路數據間的相對關系并未發生明顯變化。

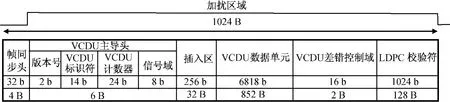
圖2 數傳幀格式Fig.2 Data transmission frame format

圖3 IQ合路加擾幀格式Fig.2 Frame format of IQ collective framing

圖4 IQ分路加擾幀格式Fig.4 Frame format of IQ respective framing

由上述分析可知：因載荷數據的組幀方式固定，每幀數據的編碼、加擾方式相同，I、Q兩路分別經相同的編碼加擾后，兩路數據間的相對關系無明顯變化。載荷數據，單載荷的高低位數據分組產生的I、Q，或多路載荷數據分別獨立組幀，都存在I、Q兩路數據間隨機性不強，數據具相似性，甚至出現大量長0、長1的缺點。

OQPSK調制所需數據為雙極性信號（數據“1”用“1”表示，數據“0”用“－1”表示）。設I路數據序列為I（n），Q路數據序列為Q（n），IQ分路組幀后加擾的設計方案無法避免數據流出現長段I（n）＝Q（n）或I（n）＝－Q（n）。

3 OQPSK調制模型

OQPSK 調制原理如圖5所示［3－5］。圖中：延遲Ts／2電路是為保證I、Q兩個支路碼元偏移0.5個碼元周期。低通濾波器（LPF）作用是對基帶信號進行限帶處理，帶通濾波器（BPF）的作用是形成OQPSK信號的頻譜形狀，保持包絡恒定。

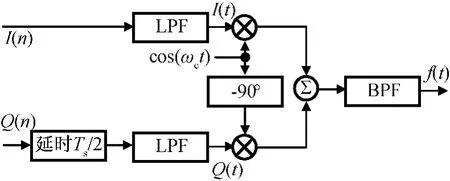
圖5 OQPSK調制器原理Fig.5 Principle of OQPSK modulation

OQPSK信號可表示為

式中：I（t），Q（t）分別為序列I（n），Q（n）的時域表示；ωc為載波頻率。

為更清楚地表示調制后的時域波形相位的變化，本文定義載波頻率ωc＝2／Ts，此處Ts為I、Q 路信號單個碼元周期。該定義不影響仿真分析的有效性，分析結果普遍適于其他載波頻率。

兩路數據及調制后的仿真結果如圖6所示。

QPSK信號兩路正交的信號為碼元同步，OQPSK調制中將正交路信號偏移Ts／2，目的是消除QPSK調制中已調信號突然相移180°的現象，每隔Ts／2信號相位只可能發生±90°的變化。因而星座圖中信號點沿正方形四邊移動，如圖7所示。

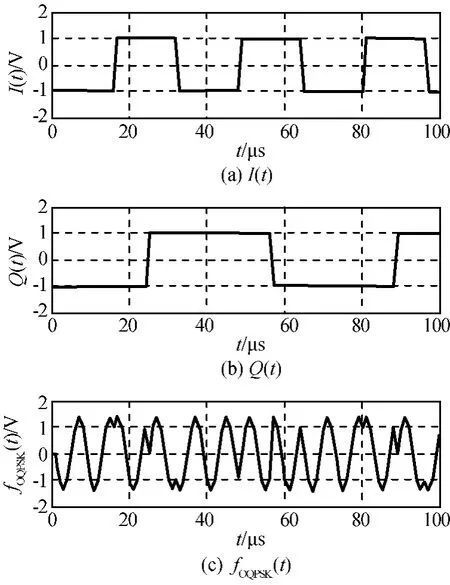
圖6 OQPSK調制時域仿真結果Fig.6 Timing simulation of OQPSK modulation

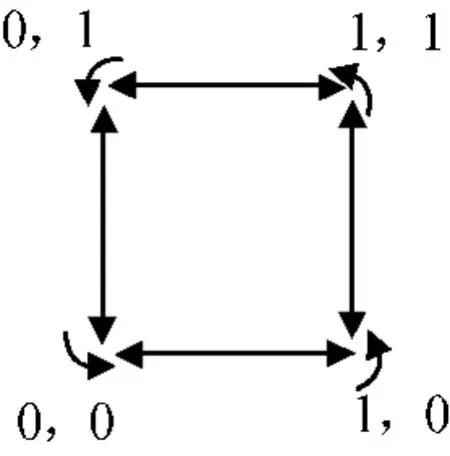
圖7 OQPSK相位轉移Fig.7 Phase transferring of OQPSK modulation

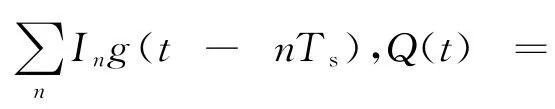
4 IQ分路加擾對OQPSK調制的影響

當I（t）＝Q（t）時，兩路數據及其調制后的時序仿真結果如圖8、9所示。由圖9可知：當I、Q兩路數據一致時，由調制后時域波形可看出載波頻率的相位變化始終為－π／2，此時OQPSK調制的相位轉移始終向逆時針方向移動。

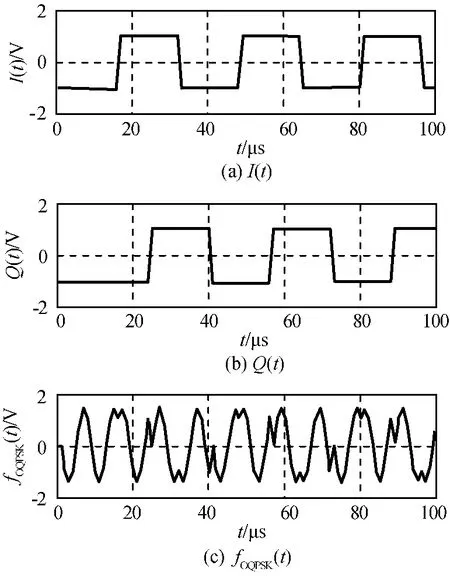
圖8 I、Q數據相同時OQPSK調制時域仿真結果Fig.8 Timing simulation and OQPSK modulation with same I／Q

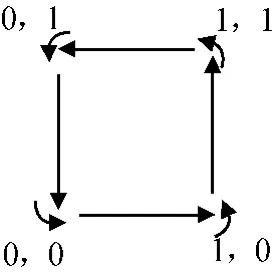
圖9 I、Q數據相同時OQPSK調制相位轉移Fig.9 Phase transferring of OQPSK modulation with same I／Q

當I（t）＝－Q（t）時，兩路數據及其調制后的時序仿真結果如圖10、11所示。由圖11可知：當I、Q兩路數據相反時，由調制后時域波形可看出載波頻率的相位變化始終為π／2，此時OQPSK調制的相位轉移始終向順時針方向移動。

4.1 數學模型

OQPSK調制信號的時域表達式為

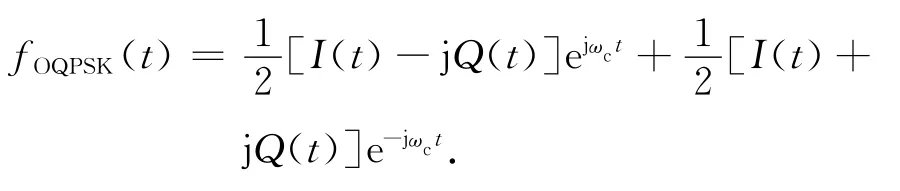
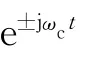
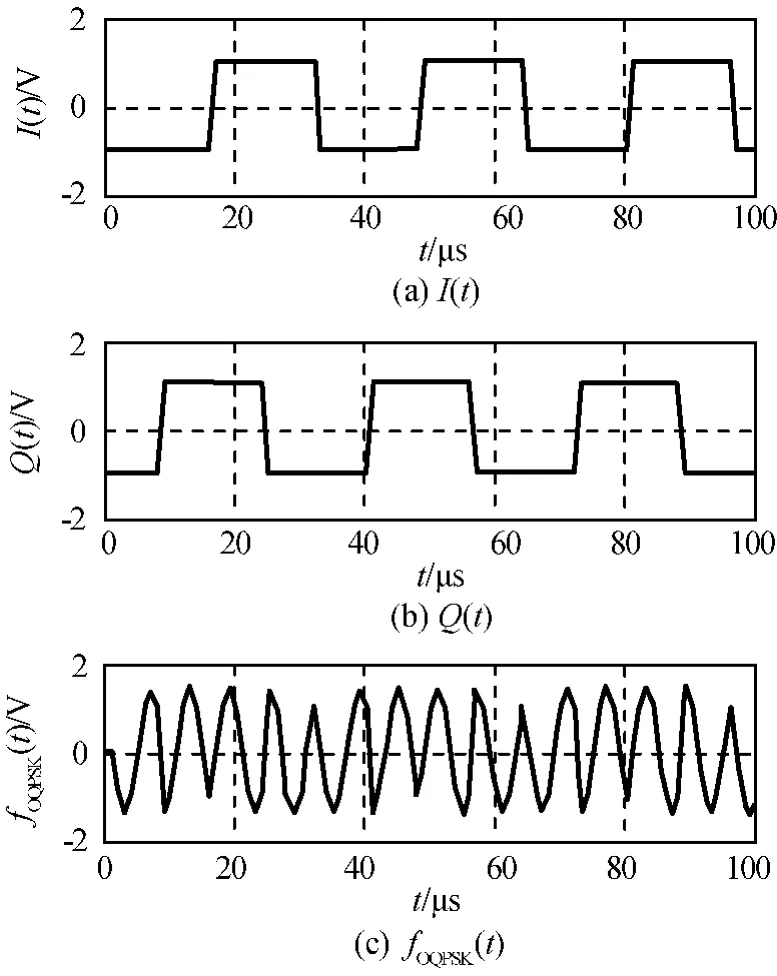
圖10 I、Q數據相反時OQPSK調制時域仿真結果Fig.10 Timing simulation of OQPSK modulation with inverse I／Q

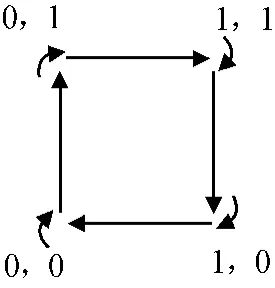
圖11 I、Q數據相反時OQPSK調制相位轉移Fig.11 Phase transferring of OQPSK modulation with inverse I／Q

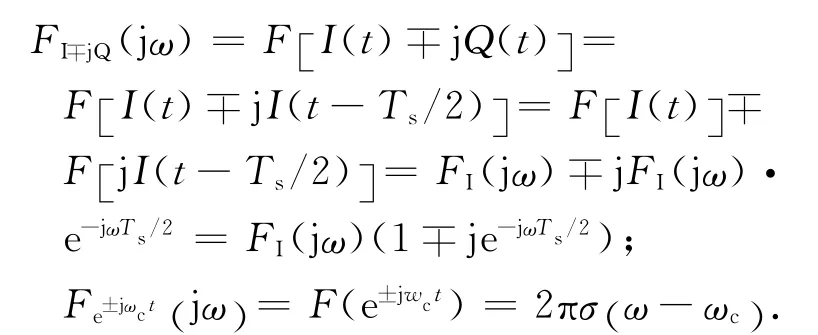
式中：σ（ω）為單位沖激函數。

OQPSK調制信號的頻域表達式為

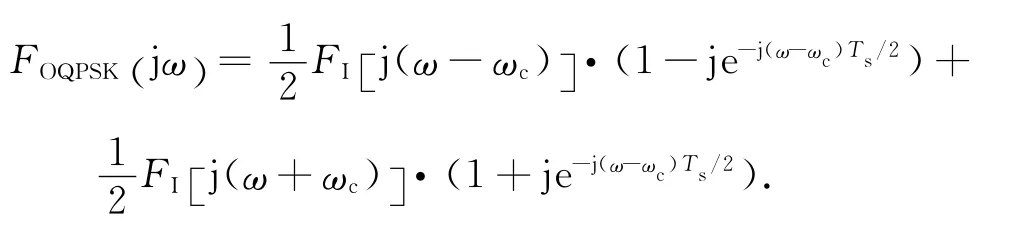
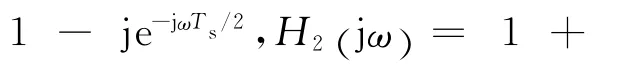
OQPSK調制信號的頻域表達式可簡化為

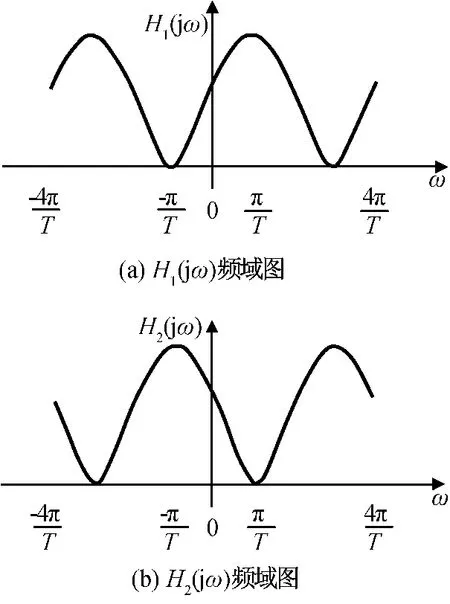
圖12H1（jω），H2（jω）頻域圖Fig.12 Frequency domain ofH1（jω）andH2（jω）

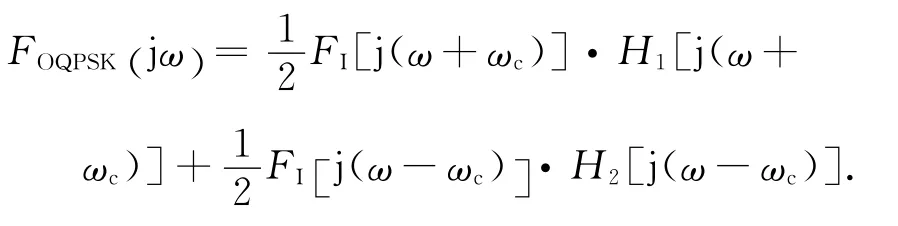
假設I路（或Q路）信號的頻譜經ωc的載波搬移后得到FI（jω）如圖13（a）所示，經 OQPSK 調制后頻譜如圖13（c）所示。由圖可知：當OQPSK調制的I、Q兩路信號相同時，相當于將I路信號的頻譜進行了H1（jω）頻域的濾波后再將頻譜搬移到載波頻率ωc。調制后的信號頻譜發生畸變，與典型的調制頻譜相比，信號主包絡頻譜在偏離載波頻率－π／Ts附近出現明顯凹陷。

當I（t）＝－Q（t）時，其 OQPSK調制信號的頻域表達式可簡化為

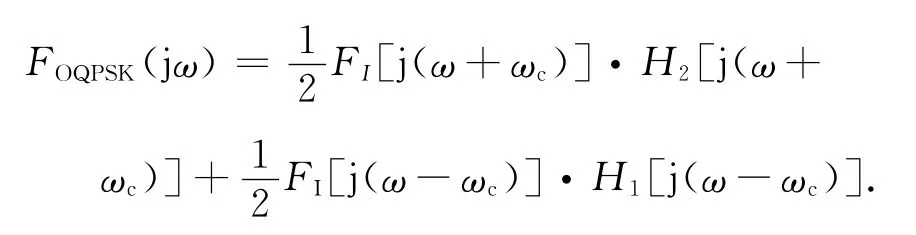
此時，OQPSK調制后的頻譜相當于將I路信號的頻譜進行了H2（jω）頻譜的濾波后再將頻譜搬移到載波頻率ωc。調制后的信號頻譜發生畸變，與典型的調制頻譜相比，信號主包絡頻譜在偏離載波頻率＋π／Ts附近出現明顯凹陷。

4.2 仿真分析

由于PN序列的隨機性，仿真中采用兩路相同的PN15序列代替I（t），Q（t）序列進行仿真分析，這樣可模擬I、Q兩路數據自身具有良好的隨機性，但兩路間存在相關性。兩路相同的PN15碼分別通過I、Q兩路送至OQPSK調制，得到頻譜圖如圖14所示。

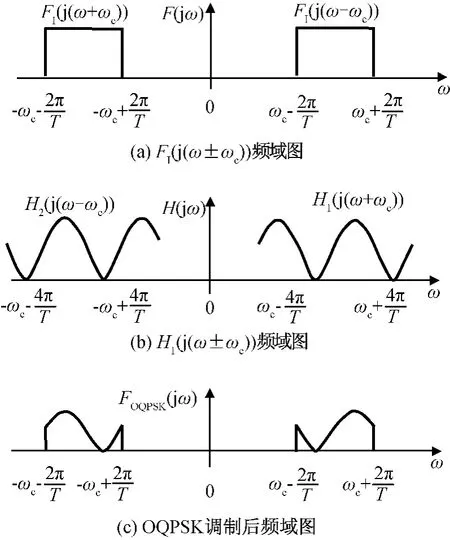
圖13 IQ數據相同時OQPSK調制信號頻譜Fig.13 Frequency spectrum of OQPSK modulation with the same I／Q

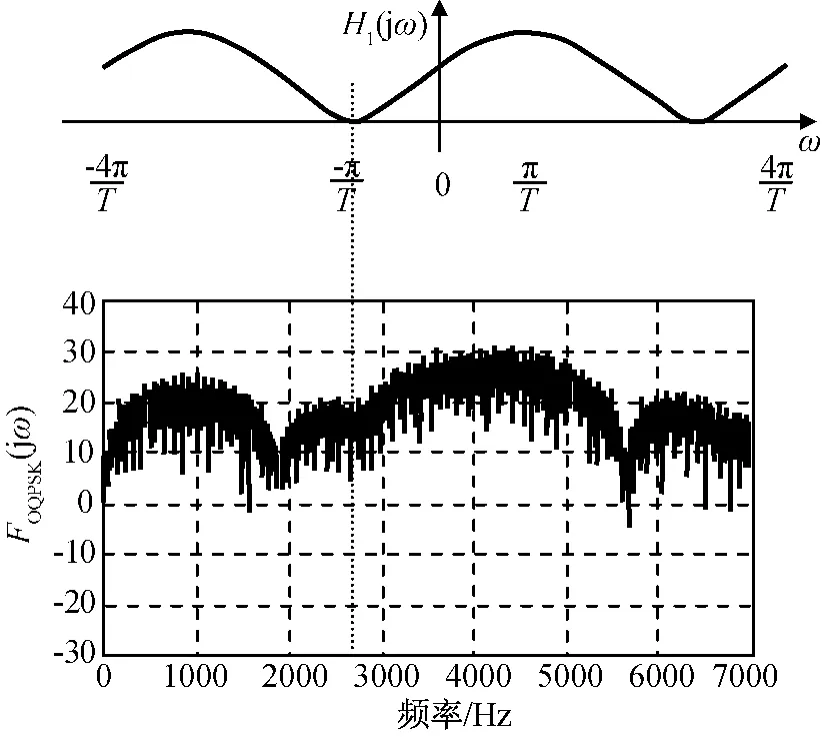
圖14 I、Q數據相同時OQPSK調制頻域仿真圖Fig.14 Frequency domain simulation of OQPSK modulation with same I／Q

由圖14可知：當I、Q數據為相同的PN序列時，經OQPSK調制后頻譜圖是將PN序列的頻域經H1（jω）頻譜的濾波后的頻譜平移到載波頻率上。OQPSK調制后頻譜在偏離載波頻率－π／Ts附近出現明顯衰減。

同樣，當I（t）＝－Q（t）時，即2路相反的PN15碼分別通過I、Q兩路送至OQPSK調制，所得頻譜圖如圖15所示。由圖15可知：當I、Q數據為相反的PN序列時，經過OQPSK調制后頻譜圖是將PN序列的頻域經過H2（jω）頻譜濾波后的頻譜平移到載波頻率上。OQPSK調制后頻譜在偏離載波頻率＋π／Ts附近出現明顯衰減。

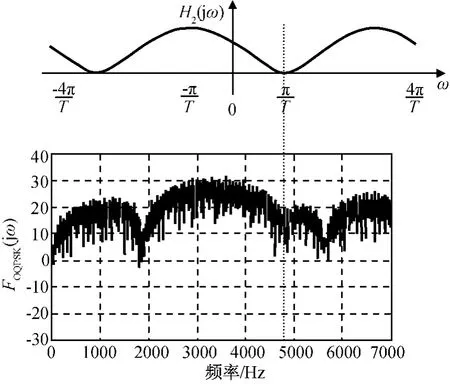
圖15 I、Q數據相反時OQPSK調制頻域仿真結果Fig.15 Frequency domain simulation of OQPSK modulation with inverse I／Q

4.3 測試結果

對仿真所示的PN碼調制信號頻譜圖進行了實際的驗證測試，兩路相同或相反的PN15序列通過調制發射機的I、Q路進行OQPSK調制，在數傳通信鏈路中通過調制發射機的輸出端進行頻譜測量，設定信道帶寬112.5MHz，頻譜圖如圖16所示。相關性，分析了載荷數據分I、Q路組幀后對

4.4 兩種加擾方式OQPSK調制信號對比

按CCSDS標準，加擾方式是按幀進行，I、Q數據合路組幀后，I、Q數據交替與1個標準的偽隨機序列相異或。這種數據流設計模型中，每路的規律性被打破，同時兩路間的規律性也被打破。單獨的I路或單獨的Q路解決了出現長“0”、長“1”碼問題，同時降低了I，Q數據間的相關性。此時，OQPSK調制的相位轉移圖沿正方形四邊移動。I、Q數據分路組幀后，僅僅解決了兩路輸入中每路的隨機性，兩路間的相關性未改變，在目標數據相似或沒有良好的隨機性情況下，相位轉移圖常有規律地向某方向移動，在頻譜上表現為頻譜失真。

由仿真和實測的頻譜圖（如圖17所示）可知：I、Q數據合路組幀既可保證每路數據的隨機性，又能實現兩路數據間相對關系的隨機性，頻譜包絡平滑完整，沒出現凹陷或凸出的頻點，適于數傳通信鏈路的數據傳輸。針對I、Q分路組幀時的頻譜變形問題，目前提出了一種新的解決方案：I、Q分路組幀后采用不同的偽隨機碼序列進行加擾，從而破壞I、Q兩路數據原本的自相關特性，達到與I、Q路數據合路組幀同樣的傳輸效果。不同的加擾方式出現兩個問題：一是數據接收端用不同的解擾方式對其進行解擾，設備不具通用性，二是為實現較好的信道傳輸效果需對兩種偽隨機碼的選擇進行分析。

5 結束語

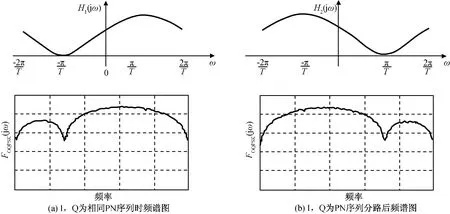
圖16 I、Q數據相同或相反時OQPSK調制后頻譜實測對比Fig.16 Contrast of OQPSK modulation frequency spectrum between same and inverse I／Q

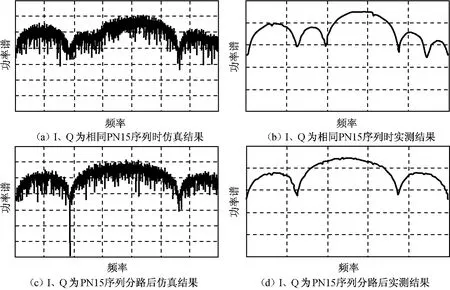
圖17 IQ不同加擾方式后的頻譜實測對比Fig.17 Contrast of frequency spectrum among different way of scrambling

本文根據OQPSK調制輸入信號I、Q路數據的OQPSK調制信號的影響。研究結果表明：在OQPSK調制方式下，僅保證I、Q兩路數據自身的隨機性并不夠，I、Q兩路數據間隨機性不足，會嚴重影響信號的傳輸質量，這種影響的特征是調制頻譜在偏離載波頻率±π／Ts附近出現明顯的衰減。

［1］ CCSDS.714.0-B-2.AOS Space communications protocol specification（SCPS）-transport protocol（SCPSTP）［S］.Washington DC：CCSDS，2006.

［2］ CCSDS.AOS space data link protocol（CCSDS 732.0-b-2）［EB／OL］.［2011-12-05］.http：／／public.CCSDS.org／publications／Standards Dev Process.aspx.

［3］ 曹志剛.錢亞生.現代通信原理［M］.北京：清華大學出版社，2003.

［4］ 吳大正.信號與線性系統分析［M］.北京：高等教育出版社，2004.

［5］ 侯光華，韋武剛.楊 森.衛星通信中的OQPSK調制技術分析［J］.無線電科技，2012（1）：13-14.