在軌服務的超近距離姿軌聯合控制研究

郭雯婷，盧 山

（1.上海航天控制技術研究所，上海 201109 2.上海市空間智能控制技術重點實驗室，上海 201109）

0 引言

隨著航天技術應用領域的飛速發展，航天器的結構和組成日趨復雜，性能與技術不斷提高，保證航天器在復雜的空間環境中更持久、穩定、高質量地在軌運行，已成為目前亟待解決的重要問題［1］。利用在軌服務技術可對復雜大型航天器進行在軌組裝以及對發生故障失效或燃料耗盡的航天器進行在軌捕獲、模塊更換、燃料加注等操作，從而可增強航天器的性能，延長航天器的使用壽命，降低費用和風險，在軌服務與操作技術有廣泛的應用前景。為實現在軌服務與操作，航天器常需經歷遠程導引、近程導引、超近程停靠、捕獲等階段，其中超近距離的相對姿態軌道聯合控制技術是實現在軌服務的核心，直接關系任務的成敗。因此，在軌服務與操作技術研究目標是解決超近距離自主逼近的相對姿態和軌道聯合控制技術。

超近距離的相對姿態和軌道聯合控制一需要設計相對姿態控制律，使服務航天器對目標航天器進行姿態跟蹤，二需要通過設計服務航天器的相對軌道控制律，使服務航天器沿目標航天器的對接端口方向逼近目標航天器。

目前，相對姿態和軌道一體化控制研究多集中于編隊衛星的相對位置姿態控制和近距離交會控制。文獻［2－4］針對編隊飛行衛星，建立了相對位置姿態的耦合動力學模型；文獻［5］針對近距離交會衛星的運動同步設計了相對位置的跟蹤控制律。但對超近距離逼近的相對姿軌聯合控制研究較少。

本文對在軌服務與目標航天器的超近距離姿軌聯合控制進行了研究。

1 相對動力學建模

為保證服務航天器在超近距離能對目標航天器特定部位進行跟蹤，其姿態控制需對目標部位進行姿態對準，即相對姿態的控制，同時相對位置仍需完成接近、繞飛等操作，因此超近距離的自主逼近和停靠控制存在姿態軌道耦合，涉及12自由度控制，需對姿態、軌道相對動力學進行建模，耦合性分析和控制律設計。

為描述服務航天器相對目標航天器的位置和姿態運動，定義如下坐標系。

a）地心慣性坐標系oi－xiyizi：原點在地心；oixi軸指向春分點；oizi軸與地球自旋軸重合；oiyi軸與oixi、oiyi軸形成正交右手坐標系。

b）航天器第一軌道坐標系：原點在航天器質心；x軸沿徑向背離地心；y軸在軌道面內垂直于x軸指向前方；z軸與x、y軸構成右手坐標系。對主動星和目標星，分別有主動星第一軌道坐標系oc－xcyczc和目標星第一軌道坐標系ot－xtytzt。

c）航天器本體坐標系：原點在航天器質心；三軸與本體固連，x軸與體縱軸重合指向前；z軸指向航天器對地面；y軸與x、z軸構成正交右手坐標系。對主動星和目標星，分別有主動星本體坐標系oc－xcbycbzcb和目標星本體坐標系ot－xtbytbztb。

1.1 相對姿態運動動力學建模

航天器繞任意點均有3個轉動自由度，需用3個獨立變量才能確定航天器在空間的姿態。本文采用相對四元數作為相對姿態的描述參數，目標航天器和服務航天器姿態運動學方程為

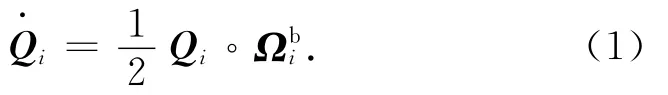
式中：i＝t，c，分別表示目標航天器和服務航天器；Qi為兩航天器本體系相對慣性系的姿態四元數；Ωbi分別為兩航天器本體系相對慣性系的旋轉角速度矢量的矢量四元數在本體系中的表示。定義相對姿態四元數Qr為目標航天器本體系相對服務航天器本體系的姿態四元數，Qt＝Qr?Qr，則

式中：符號“＊”表示共軛。

兩航天器的絕對姿態動力學方程為

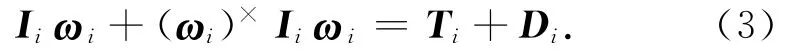
式中：ωi為兩航天器相對慣性系的旋轉角速度在其本體系中的表示；Ii為兩航天器的轉動慣量在其本體系中的表示；Ti為作用于兩航天器的控制力矩；Di為兩航天器的外部干擾力矩；符號“×”表示斜對稱矩陣。

為使相對姿態與絕對姿態的運動學方程形式一致，定義相對角速度為目標航天器本體相對服務航天器本體的相對旋轉角速度在服務航天器本體系中的表示，有

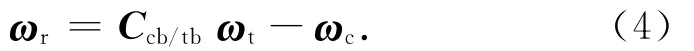
式中：Ccb／tb為由目標航天器本體系至服務航天器本體系的轉換矩陣。對式（4）求導并以矩陣形式表示，則有

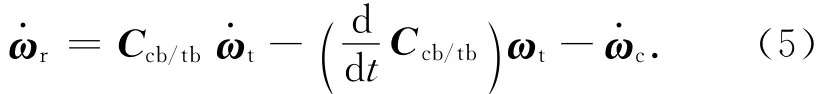
式中：

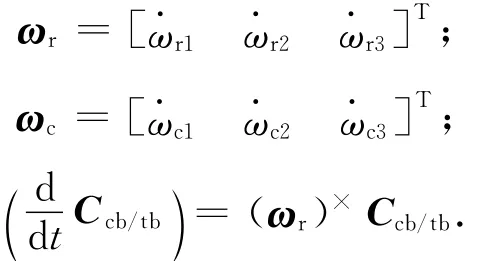
則有

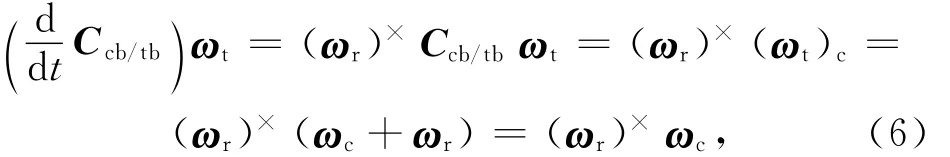
進而有

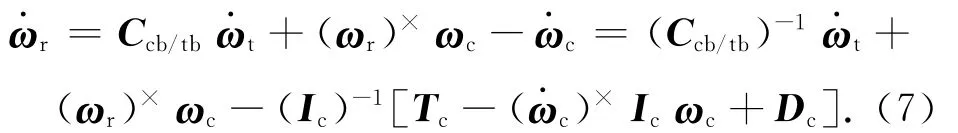
因此，相對姿態動力學方程為：

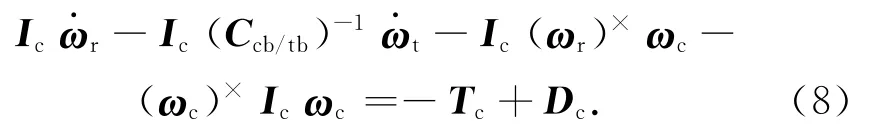
由式（8）可知：相對姿態運動可通過Tc控制。

1.2 相對軌道動力學建模

在地心慣性坐標系中，兩航天器的絕對軌道動力學方程可表示為

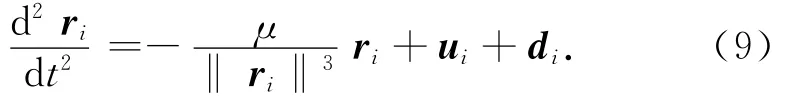
式中：ri為兩航天器地心距矢量；ui為施加于兩航天器的控制加速度矢量；di為兩航天器攝動加速度；μ為地球引力常數。

兩航天器絕對軌道動力學方程相減，并令rcrt＝rct＝l＋ρ，可得精確的相對軌道動力學方程為

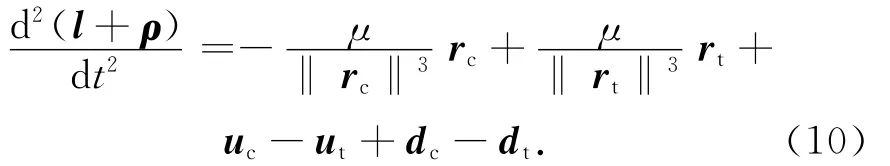
式中：l為目標航天器到控制目標點的位置矢量，可根據最終逼近段的要求與約束條件進行軌跡設計；ρ為控制目標點至服務航天器的相對位置矢量，如圖1所示。

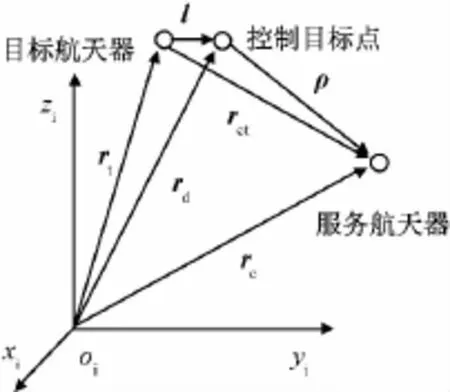
圖1 相對位置矢量Fig.1 Relative position vector

根據在活動坐標系中矢量導數的規則，將式（10）在目標航天器第一軌道系中投影可得

式中：（ωt）t，）t分別為目標航天器軌道坐標系的絕對角速度和角加速度，其在ot－xtytzt系中的投影分別為（1＋etcosθt）2。此處：θt為服務航天器的真近點角，且。其中：pt，et分別為服務航天器半通徑和偏心率。將式（11）化為狀態變量形式

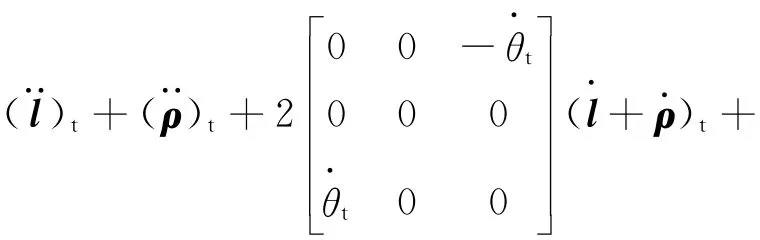
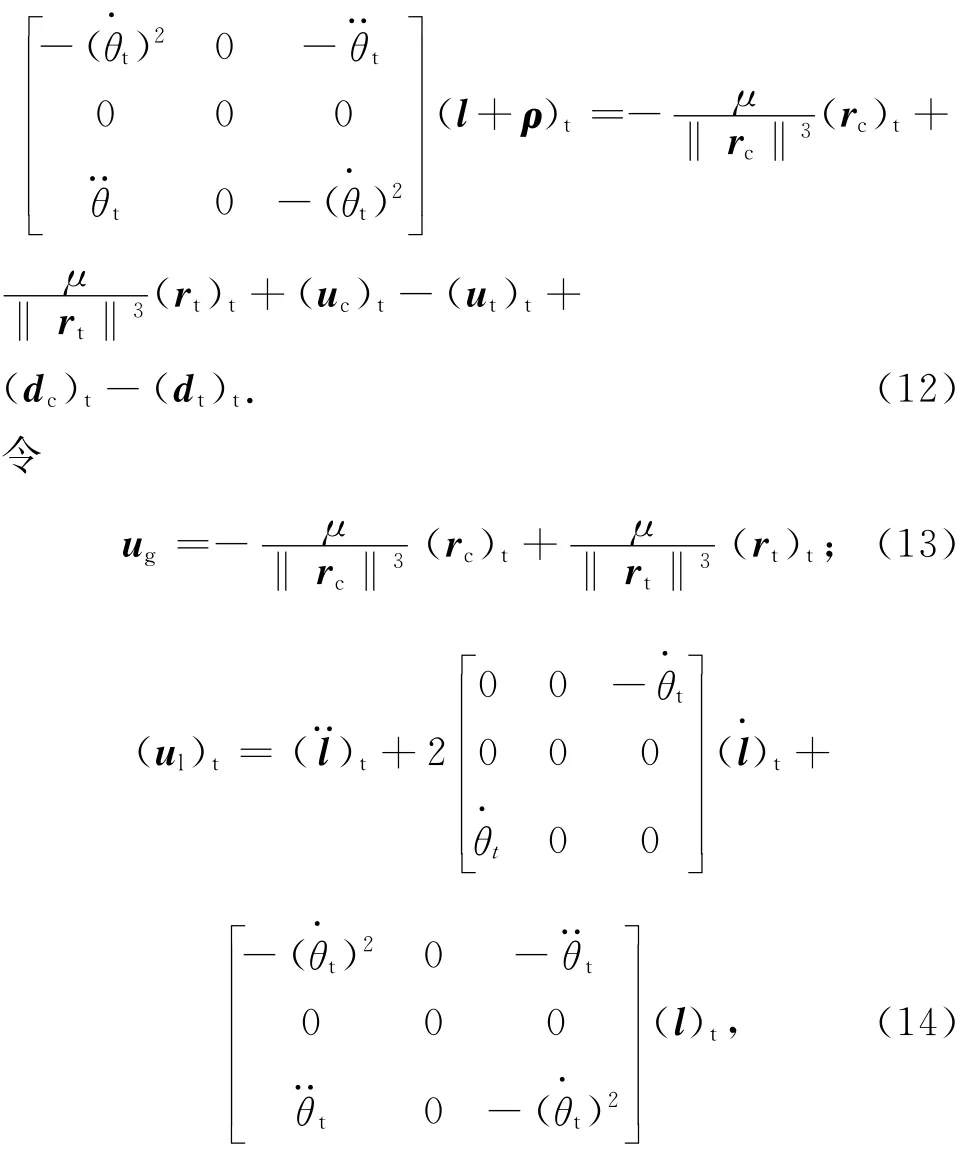
則完整的相對軌道動力學方程為

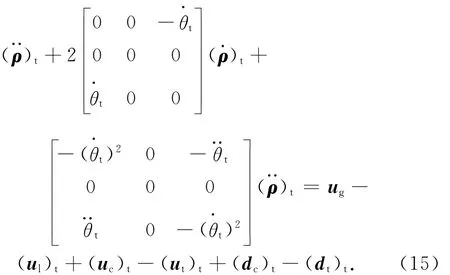
對服務航天器和目標航天器超近距離的相對運動，ρ為小量，對ug項通過取一階近似（線性化）進行簡化。由ρ＝［xyz］T，（rt）t＝［0 0 －rt］T，（rc）t＝［xyz－rt］T，將ug項改寫為分量形式

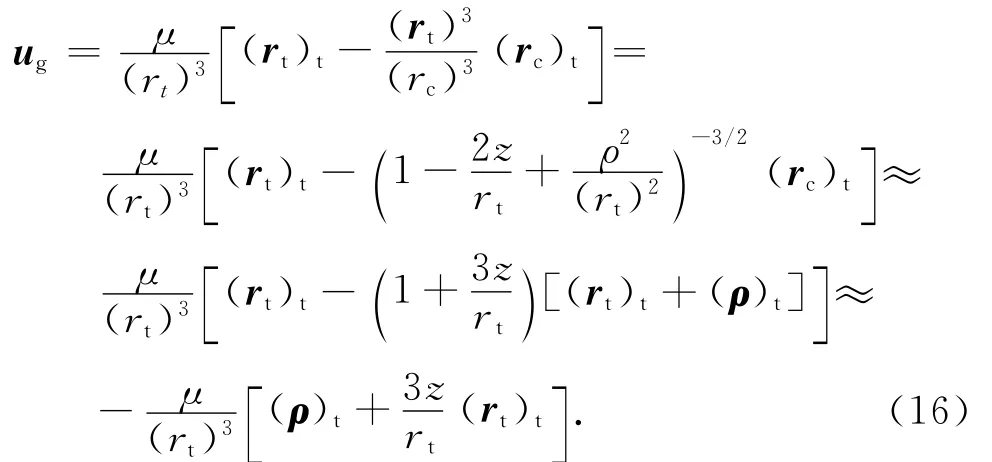
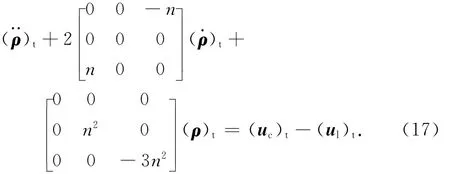
1.3 姿態軌道耦合性分析

服務航天器自主逼近與捕獲目標航天器過程中，相對姿態與軌道耦合，主要包括以下耦合。

a）服務航天器推力器沿本體安裝，相對軌道動力學建立在目標航天器軌道系中，需將控制加速度轉換至服務航天器本體系中，該轉換與姿態相關，稱為控制輸出耦合。其轉換矩陣

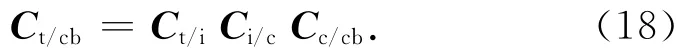
式中：Ct／i為慣性系至目標航天器軌道系的轉換矩陣；Ci／c為服務航天器軌道系至慣性系的轉換矩陣；Cc／cb為服務航天器本體系至軌道系的轉換矩陣。

b）相對位置和相對速度的跟蹤指令（即設計的逼近路徑）隨目標航天器姿態而變。此耦合是由控制指令產生的，稱為控制指令耦合。其轉換矩陣

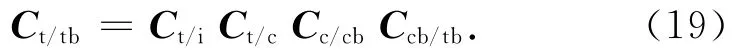
式中：Ccb／tb為服務航天器相對目標航天器的姿態轉換矩陣，可由相對測量獲得的目標航天器相對服務航天器的姿態轉換矩陣求逆得到。

c）需將相對測量獲得服務航天器本體系中目標航天器相對服務航天器的位置、速度轉換至目標航天器軌道系中進行控制，該轉換與服務航天器自身姿態有關，稱為控制輸入耦合。有

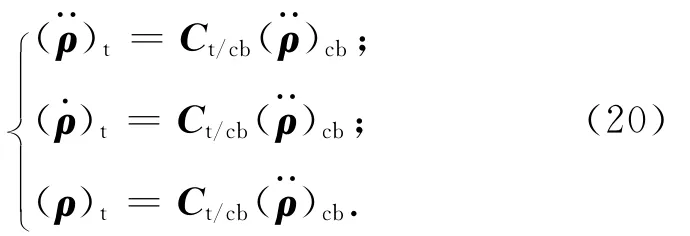
2 超近距離姿軌聯合控制設計

超近距離段一般從服務航天器與目標航天器相距300～100m開始，直至兩航天器零距離接觸，實現對接或抓捕。該階段具有相對距離近、安全性突出、相對控制精度要求高、控制周期短等特點。近程導引段兩飛行器距離相對較遠，變軌燃料最少是主要設計因素，超近距離段則主要考慮安全性和控制精度。

在超近距離段，服務航天航天器一般沿視線方向以準直線軌跡逼近目標航天器，根據飛行軌跡安全性，相對導航視場角，以及捕獲與對接的技術要求，實施相對狀態自主控制［6－7］。相對狀態及其變化率由相對導航系統獲得。

2.1 相對姿態控制律

設目標航天器相對自身軌道坐標系保持姿態穩定，其控制力矩僅用于穩定自身姿態，為最終平移段的接近創造條件，并不直接參與交會對接相對姿態機動；服務航天器以目標航天器姿態為目標姿態（期望姿態），根據相對姿態四元數和相對旋轉角速度進行姿態控制，實現對目標的姿態跟蹤［8］。

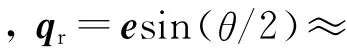
根據相對姿態動力學方程，設計非線性反饋控制律由非線性反饋項Tc1（用于抵消耦合力矩）和四元數與角速率線性反饋項Tc2兩部分組成，即

式中：

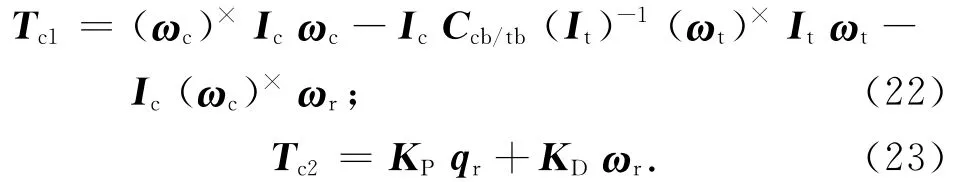
此處：KP，KD為反饋增益系數矩陣，且KP＝kpIc；KD＝kdIc。其中：kp，kd為反饋增益系數。將式（21）代入式（8），則有

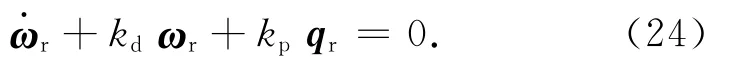
根據q1，qr的簡化，可得

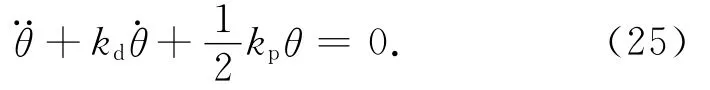
顯而易見，此為典型的線性二階系統方程，根據系統的動態響應要求，選擇適當KP，KD便可使控制系統穩定。

2.2 相對軌道控制律

2.2.1 基于LQG的實時閉環反饋軌道控制算法

為實現高精度的相對軌道控制，采用最優實時閉環反饋控制方法，以預先設計的路徑作為參考量，確保每個控制周期內航天器都能跟蹤預期的相對軌跡。

根據相對軌道動力學方程，選擇狀態向量

則可寫成狀態空間形式

式中：u＝Ct／cb（uc）cb－Ct／cb（ul）tb；

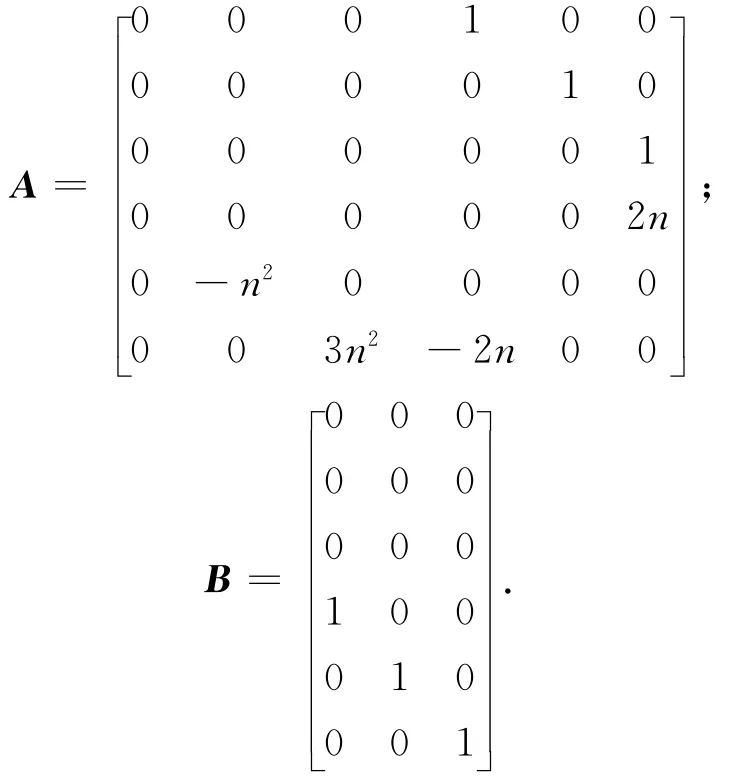
超近距離的相對軌道控制是尋找合適的軌道控制律uc將式（27）中的X控制為0。此為狀態調節器問題，可用現代控制理論中的線性二次型調節器（LQR）進行設計［9］。

離散化式（27），得

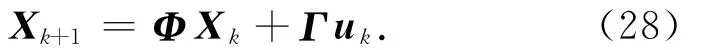
尋找線性系統式（28）的最優狀態反饋控制律uk＝－KXk，使二次型目標函數

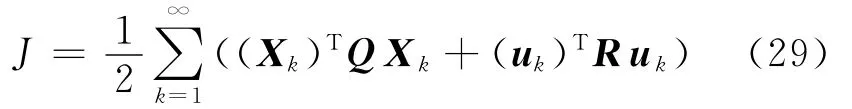
達到最小。此處：Q，R分別為狀態量和控制量的加權矩陣。

根據極小值原理，可得LQR最優控制律的狀態反饋增益矩陣

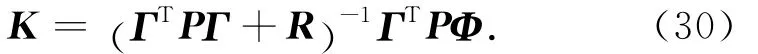
式中：P為對稱非負定矩陣，滿足離散Riccati方程

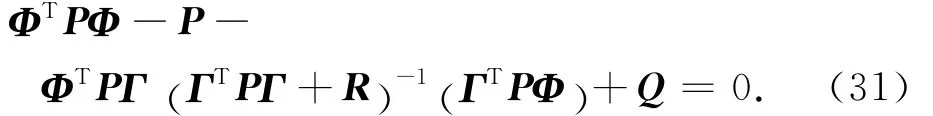
由uk反解出作用在服務航天器本體系上的控制加速度

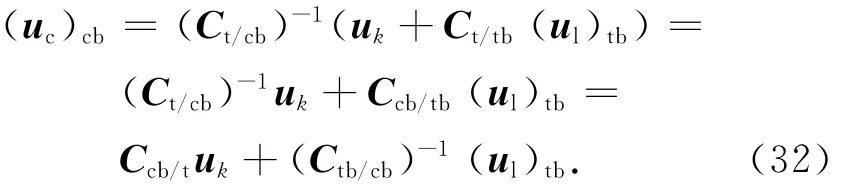
2.2.2 相對運動軌跡

由自主閉環軌控可知，LQG控制算法使服務航天器在逼近目標航天器時，控制目標點存在一個突變過程，速度量（ul）t及相對狀態量發生突變會直接導致控制加速度發生突變，進而易造成控制超調，因此需進行軌跡設計。逼近軌跡設計主要用于接近目標特征部位，為最后在軌操作或對接創造條件。傳統的逼近軌跡在相對軌道動力學影響下為曲線，故在逼近過程中會造成視場角變化，不利于相對跟瞄設備持續跟蹤目標，在超近距離內可能會造成目標丟失發生碰撞的危險。采用直線逼近方式，給定逼近的時間與目標點，按某種函數規律平滑變化，可設計出一條直線逼近軌跡，在逼近的起始點和終端點滿足邊值條件，軌跡上每點都可得到期望的相對位置和相對速度，將其輸入控制系統進行相對軌跡控制，可使每一時刻服務航天器均在期望的位置，并具期望的相對速度，避免與目標發生碰撞。同時，直線逼近可保證目標始終處于服務航天器的某一方向，利于相對跟瞄設備對目標的穩定跟蹤，提高任務的可靠性。

先設計l的y、z分量為

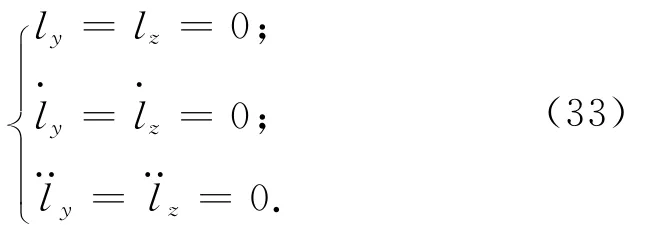
則在目標飛行器軌道坐標系中，控制目標點在y、z向的坐標始終保持為0，服務航天器相對目標的運動軌跡始終保持在x軸附近。

其次合理設計控制目標點l的x分量，使其按某種函數規律平滑變化，同時在逼近的起始點和終端點滿足邊值條件。x分量的設計可歸為一個兩個邊值條件問題，此兩點邊值問題有無窮多解。設lx劃分為下列4個階段。

a）加速段，采用等加速度進行加速逼近；

b）等速逼近段，利于服務航天器快速安全地逼近目標航天器；

c）速度衰減段，在短時間內速度衰減到較小的量值，為停靠或對接做準備；

d）慢速靠攏段，在對接前的最后數米，以較小的速度靠攏，利于在軌操作［10－11］。

設計靠攏速度為：在最后靠攏階段，無論制導機動正常與否，服務航天器與目標航天器的接觸速度在安全范圍內，不會造成危險。設計的逼近軌跡如圖2所示。

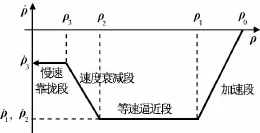
圖2 逼近軌跡設計Fig.2 Trajectory design for proximity relative motion

將設計的軌跡作為控制系統的參考輸入，通過自主閉環反饋控制律對服務航天器軌道狀態施加反饋控制，使其始終保持在目標軌道系中的設計點處。因該軌道控制作用為連續狀態反饋，故其精度較高。

2.2.3 脈寬調制

因LQG算法獲得的軌道控制加速度為連續的，但服務航天器配置的推力器只能提供恒定推力，為此本文采用脈沖調寬算法。脈沖調寬本質是通過控制定常推力發動機在每個控制周期內的工作時間，以保證發動機實際作用沖量與控制律在該控制周期內的所需沖量相等。具體的實現方法為：根據LQG軌道控制算法求出作用于服務航天器的控制力加速度為（uc）cb，則在采樣周期內，3個方向上作用于服務航天器的沖量分別為

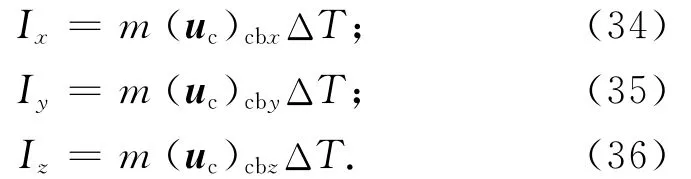
式中：m為服務航天器質量；ΔT為軌控周期。根據確定的控制加速度，按采樣周期內沖量相等原則，3個方向上發動機推力作用時間分別為

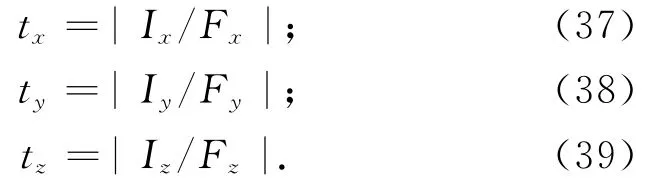
式中：Fx，Fy，Fz為三個方向的軌控推力。若發動機能提供的最小脈沖寬度為ΔTmin，采樣周期為ΔT，則對tx，ty，tz進行處理

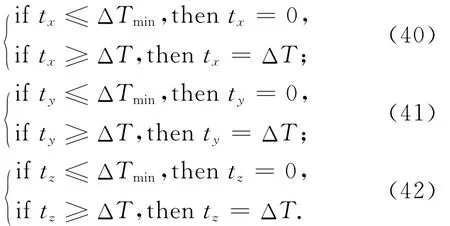
此即為用恒定推力模擬連續軌控加速度的脈沖調寬算法。

3 數學仿真

仿真中航天器初始軌道要素見表1，服務航天器從目標航天器正后方200m接近至目標0.5m。取仿真時間1 000s，仿真步長0.1s，用本文方法所得超近距離段姿態軌道聯合控制的仿真結果如圖3～7所示。

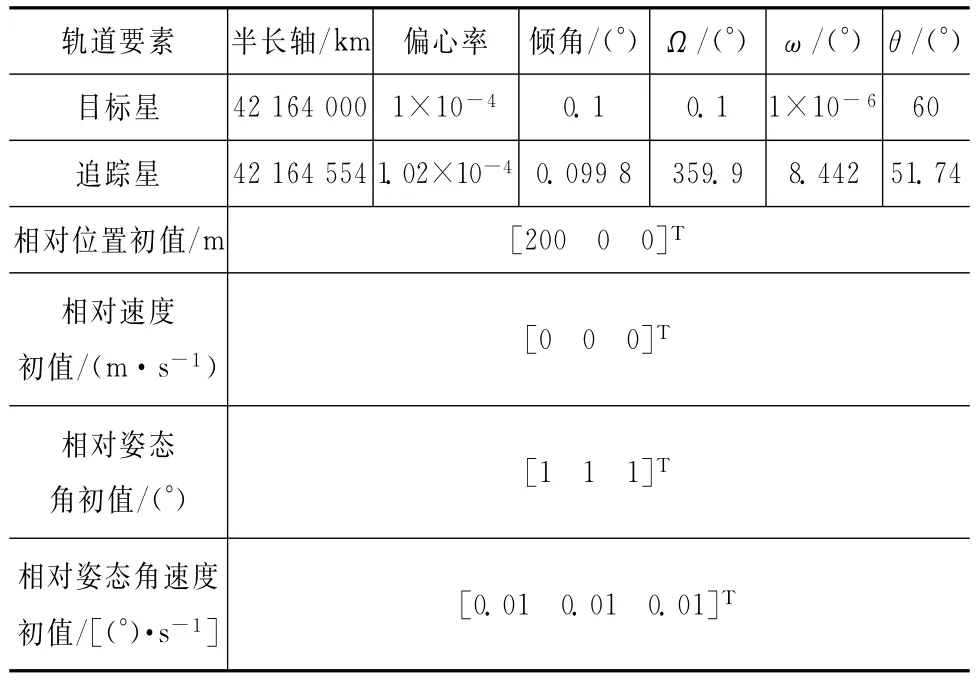
表1 兩航天器初始參數Tab.1 Initial elements of two spacecraft

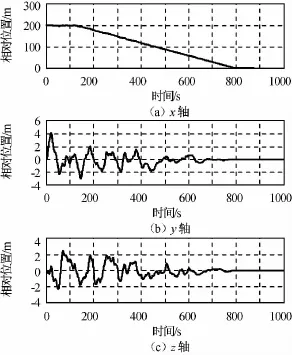
圖3 相對位置Fig.3 Relative position

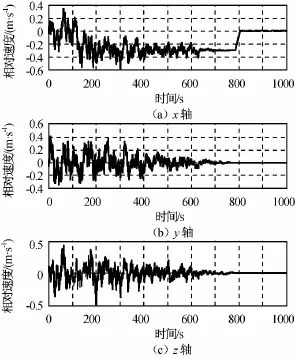
圖4 相對速度Fig.4 Relative velocity

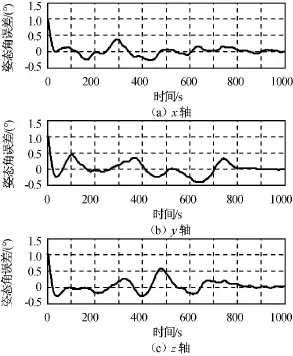
圖5 相對姿態角控制誤差Fig.5 Relative attitude angular position error

由圖可知：經約800s服務航天器從目標航天器正后方200m直線逼近至0.5m處，相對位置控制精度優于0.15m，相對速度也逐漸趨于零；目標航天器相對服務航天器的三軸姿態角控制精度優于0.5°，三軸姿態角速度控制精度優于0.02 （°）／s。仿真表明，本文的相對軌道和姿態聯合控制算法可行，且控制性能較好，滿足高精度交會對接的需求。

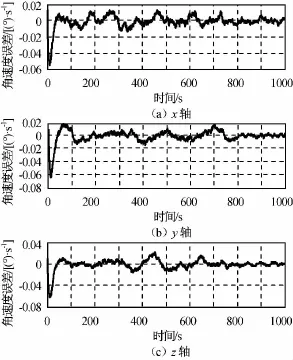
圖6 相對姿態角速度控制誤差Fig.6 Relative attitude angular velocity error

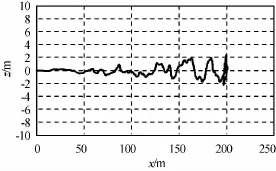
圖7 軌道平面內相對運動軌跡Fig.7 Trajectory of relative motion

4 半物理仿真

為進一步驗證本文超近距離姿軌聯合控制方法的正確性，用地面半物理仿真試驗進行驗證。超近距離姿軌聯合控制試驗系統所用的仿真平臺由零重力氣浮臺、目標星模擬器、追蹤星模擬器、目標與測量定位系統、地面控制臺、動力學宿主機、動力學目標機和視景仿真計算機等組成。其中：氣浮平臺上的衛星模擬器模擬失重環境中的動力學；仿真計算機根據相對狀態量和逼近、懸停的任務規劃，解算控制律，并控制追蹤星模擬器按指定路徑運行；視景仿真系統演示在軌飛行器的運行狀態。在與數學仿真參數相同的條件下，半物理仿真結果如圖8所示。分析試驗數據可知：模擬器的相對位置控制精度最終優于1cm，相對姿態控制精度優于0.1°，滿足最終的對接、捕獲控制精度的需求。

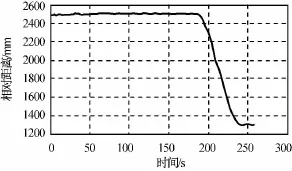
圖8 主動星模擬器相對距離Fig.8 Relative distance

5 結束語

本文對在軌服務的超近距離姿軌聯合控制方法進行了研究。建立了兩航天器超近距離相對運動中，兩航天器基于相對四元數的相對姿態運動動力學方程和基于相對運動軌跡設計的相對軌道動力學模型，根據動力學模型耦合特性，設計非線性相對姿態控制律，并考慮姿態運動的耦合作用，設計了具有姿態信息反饋的較強魯棒性的控制律，以獲得高精度的交會對接控制。數學仿真和半物理仿真結果驗證了方法的有效性和可行性。

［1］ 陳小前，袁建平，姚 雯，等.航天器在軌服務技術［M］.北京：中國宇航出版社，2009.

［2］ SEBASTIAN G.Modeling the coupled translational and rotational relative dynamics for formation flying control［R］.AIAA，2005－6091.

［3］ PAH H，KAPILA V.Adaptive nonlinear control for spacecraft formation flying with coupled translational and attitude dynamics［C］／／Proceedings of the 40thIEEE Conference on Decision and Control.New York：IEEE，2001，3：2057－2062.

［4］ 吳云華，曹喜濱，張世杰.編隊衛星相對軌道與姿態一體化耦合控制［J］.南京航空航天大學學報，2010，42（1）：13－20.

［5］ SUBBARAO K，WELSH S.Nonlinear control of motion synchronization for satellite proximity operations［J］.Journal of Guidance，Control，and Dynamics，2008，31（5）：1284－1294.

［6］ PHILIP N K，AANATHASAYANAM M R.Relative position and attitude estimation and control schemes for the final phase of an autonomous docking mission of spacecraft［J］.Acta Astronautica，2003，52（7）：511－522.

［7］ CLAUDINON B，MARCHAL P，FEHSE W.Control techniques for rendezvous and docking：IFAC Automatic Control in Space［C］.Toulouse：1985.

［8］ 朱仁璋.航天器交會對接技術［M］.北京：國防工業出版社，2007.

［9］ 李國勇.最優控制理論及參數優化［M］.北京：國防工業出版社，2006.

［10］ 朱仁璋，尹 艷.論空間交會最終平移段制導設計［J］.中國空間科學技術，2004，24（5）：1－8.

［11］ 朱仁璋，湯 溢，尹 艷.空間交會最終平移軌跡安全模式設計［J］.宇航學報，2004，25（4）：443－448.