分離模塊化航天器系統評估和優化設計研究

徐 明，王金龍

（1.北京航空航天大學 宇航學院，北京 100191；2.中國民航大學 空中交通管理學院，天津 300300）

0 引言

F6是美國國防高級計劃研究局（DARPA）對分離模塊概念進行研發驗證項目［1］。DARPA對其技術性能和經濟優勢進行了廣泛的研究，投資Lock－heed Martin Company（LM），Northrop Grumman Corporation（NG），Orbital Sciences Corporation（OSC），Boeing Company（BC）等四家公司以價值為中心的設計方法進行F6項目的第一階段工作，于2009年2月準時完成［2］。第二階段的工作于2009年11月啟動，由OSC公司負責。同時DARPA表示會于2013年實現在軌演示驗證。通過F6項目的不斷深入研究，研究人員提出了以價值為中心的航天器設計方法（VCDM）［3］。VCDM 通過對壽命期、技術風險、不確定性的多方面考慮，獲取最高的投入產出比，達到以最小成本獲取最大價值的目標。此方法通過對能力、成本和風險的價值化將設計的技術屬性轉化到商業范疇，以“凈現值”權衡系統優劣［4］。文獻［5］研究實現分離模塊方式的太空快速響應系統面臨的問題，從技術、組織機構支持、經濟和政治四個方面進行分析并研究其內在聯系。文獻［6－7］總結F6項目中取得的成果，對設計方法進行合理化并討論以價值為中心的設計標準與傳統的系統工業過程標準的聯系，評價以價值為中心的設計在F6項目中的重要性，重述分離模塊航天器的概念，比較分離模塊航天器與傳統整天航天器的優缺點，并介紹一系列分離模塊航天器的設計制造的以價值為基礎的技術方法。文獻［8］對分離模塊航天器和傳統航天器進行屬性、策略、模型比較，評價分離模塊航天器的成本和價值優勢。文獻［9］比較分析了四家公司設計的VCDM工具模型構架、風險和凈現值量化等的工具特征，對參與F6項目第二階段OSC公司研發的PIVOT工具進行跨學科優化，通過動態生命周期仿真和參數模型評估生命周期成本影響，用非參數的計算機物理模型評估航天器的質量影響，研究結果表明分離模塊航天器的生命周期成本較傳統整體航天器有優勢。文獻［10］研究能解決F6項目結構兩個難題的設計工具GT－FAST，用實例分析FT－FAST設計工具處理輸入、模型、屬性、假設的方式。隨著分離模塊航天器設計的發展，國內許多學者也開始研究相關項目。文獻［11］介紹了分離模塊航天器的概念和進展，分析和探討了以價值為中心的航天器設計，對國內的分離模塊航天器發展提出啟示和建議。文獻［12］針對航天器概念設計階段的不確定多學科設計優化進行研究，驗證其可行性和有效性。

本文對分離模塊化航天器系統評估和優化設計進行了研究。

1 成本、價值及評估指標

航天器的設計成本包括航天器研制成本和發射運營成本，同時也包含了各種不確定因素存在而可能發生的成本。所有的成本統一量化為貨幣單位形式進行統計。從航天器設計的準備階段至其生命周期結束的所有成本的總和構成分離模塊航天器的總成本。

VCDM研究的前提是將航天器設計的技術價值定量，每種以價值為中心的航天器設計方法中均有價值化準則對航天器進行價值評估計算，將航天器的實際應用技術轉化為定量價值。對價值的定量評估并非絕對測量，而是作為一種評估工具，為任務決策提供信息。在以價值為中心的航天器設計過程中，通過價值量化準則對航天器進行價值量化，考慮不確定性因素對價值生成的影響，直到航天器生命周期結束所獲取的價值之和為航天器的總價值。

F6第一階段項目中，四家公司采用不同商業指標對航天器的成本與價值收益進行評估，不同商業指標的側重點各異。凈現值（NPV）廣泛用于經濟、金融、會計等領域，是評價設計方案優劣的一種方法。NPV不僅權衡成本與價值收益，而且考慮方案的執行時間問題，反應方案的時間效率。方案決策者通過對NPV的值進行方案決策，決策法則為：凈現值為正則采用，凈現值為負則不采用，多個備選方案決策時挑選正值最大的方案。為更好地評估航天器系統，本文采用NPV作為評估指標。分離模塊航天器系統設計方案優劣以NPV大小衡量，NPV值大表示投入成本少，產出收益大，設計方案優；反之，設計方案劣。引入VCDM 航天器設計中，以NPV值大小權衡航天器的總體投入產出比。NPV可表示為

式中：DR為貼現率；N為凈現金流；Tyearloop為航天器生命周期。

2 航天器研制模型

2.1 分離模塊航天器的體系結構建模

航天器體系結構建模是對航天器成本和價值收益評估的前提。分離模塊航天器系統因其結構特征與傳統航天器有較大不同，故其體系結構建模也截然不同。國內外分離模塊航天器的體系結構建模研究中，較常見的對分離模塊航天器層次的定義，從低到高依次為組件、模塊、星簇，如圖1所示［12］。

組件在航天器中能獨立完成某項任務，是分離模塊航天器建模中的最小單位。在DARPA的第一階段任務中，四家公司分別對組件進行建模，主要包括以下。

a）任務的有效載荷。分離模塊航天器設計和價值評估最終目標是小成本獲得高價值，價值獲取的唯一途徑是有效載荷。有效載荷通過任務完成獲取價值，而不同的任務需要不同的有效載荷完成，如對地觀測有效載荷（EO）。

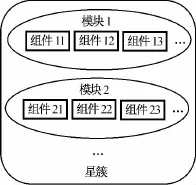
圖1 組件、模塊和星簇關系Fig.1 Relationship among component，module and cluster

b）測控組件，通過中繼衛星實現對星簇的連續測控。

c）任務數據處理組件，星上高性能計算機，用于處理復雜的任務數據。

d）數傳通信組件，星上負責星星間、星地間通信和數據下載上傳的組件。

e）數據存儲組件，如固態硬盤，主要功能為存儲有效載荷完成任務而產生的大量數據，為數據傳輸做準備。在建模階段通過經驗和設備參數對各組件進行屬性賦值，如質量、功率、成本、技術成熟度等。

模塊由多個組件構成，可在空間中實現獨立自由飛行。構成模塊的組件除有效載荷等功能性組件外，還包括電源、熱控等衛星平臺的相關組件。模塊的屬性取決于其組件和平臺的屬性，在對組件進行建模并整合后可得到模塊的屬性。

星簇即分離模塊航天器，由多個分離模塊編隊飛行構成，完成某項或某些目標任務。

航天器系統總體設計包括航天器星體設計和發射運載設計，航天器發射運載方案的建模是航天器系統必不可少的部分。本文發射運載器選擇Minotaur I，Athena I，Taurus 2210，Taurus 3110，Minotaur IV，Athena II。發射運載器不同，發射運載能力和可靠性亦不同，發射運載成本會相應有所不同。在發射運載設計方案中，應根據模塊設計適當選擇。

模塊中分離組件的組合、星簇中模塊的分割、運載發射設計均會對航天器的成本和價值評估產生影響。航天器的成本與價值的評估對模塊中分離組件的組合、星簇中模塊的分割和運載發射設計進行優化，使航天器能獲得更高的投入產出比。

2.2 航天器系統評估模型

2.2.1 成本模型

分離模塊航天器成本主要考慮模塊研制成本、發射與運營成本和風險成本三部分。其中：航天器的商業保險成本歸入發射與運營成本，暫不考慮地面設備成本與軟件開發成本；風險成本考慮由于各種不確定性因素而出現的模塊研制時間推遲、發射運載失敗、在軌故障等情況維護而需要投入的成本。

成本按屬性可分為不可循環和可循環兩種，對應有子系統中的可循環使用部件設計和不可循環使用部件設計。這種分類設計主要針對部分方案可重復使用的設備，在第一次計算成本后，第二次的成本核算可在第一次的基礎上乘以學習曲線率系數即為第二次使用的成本。分離模塊航天器在生命周期內成本計算流程如圖2所示。

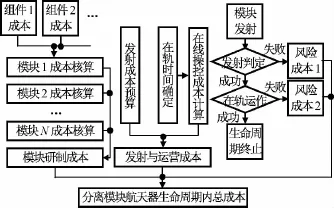
圖2 成本計算過程Fig.2 Procedure to estimate cost during life

a）模塊研制成本

航天器總體設計中含有不同的組件模塊，不同組件模塊的成本各異，同類模塊因技術成熟度與研制時間不同也會出現差異。在成本核算中用可循環與不可循環成本分類分別計算。在同一類模塊進行研制時，第1個模塊包含技術不成熟帶來的較高成本，同一類模塊的后續研制成本因可循環部件的成本而相對減少。

考慮批量生產，單元模塊的成本估算為

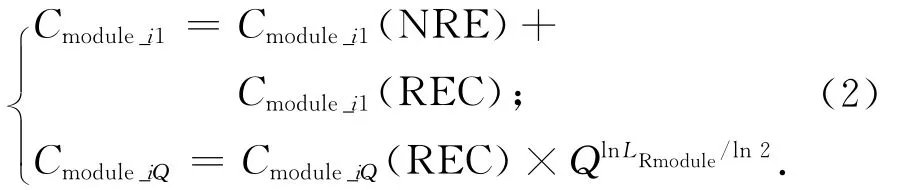
式中：Cmodule_i1為第i類模塊中第一個模塊的研制成本，包括不可循環使用成本Cmodule_i1（NRE）和可循環使用成本Cmodule_i1（REC）兩部分；Cmodule_iQ為同類型第Q個模塊的成本；LRmodule為該類模塊研制生產的學習率。模塊給重復成本和重復成本通過模塊所攜帶組件成本進行估算，成本估算公式參考小衛星成本模型（SSCM07）。

令通貨膨脹引起的第i類中第Q個模塊研制成本溢值為Cmodule_iQ_inflated，有

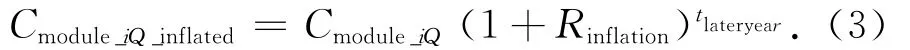
式中：Rinflation為年通脹率；tlateryear為模塊研制年時間。所有模塊的研制成本

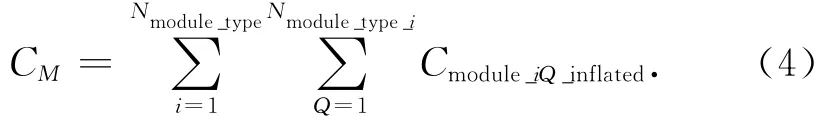
式中：Nmodule_type為分離式航天器包含的所有模塊類型數；Nmodule_type_i為第i類模塊數。

b）發射與運營成本

發射運載方案根據模塊屬性進行設計，方案確定后模塊的發射運載成本按方案執行成本統計。航天器在總體設計中會對發射運載器產生潛在的約束，有效載荷的安裝等限制模塊發射的自由組合。不同模塊可組合發射，因此發射次數不大于模塊個數。

由于發射運載器成本巨大，在技術條件允許時應盡可能減少發射次數，在發射運載器運載能力范圍內采取多個模塊同一運載器發射。總發射成本為每次發射成本之和。

分離模塊航天器在軌運行時，每個模塊都可視作獨立小衛星，因此在運營成本中按模塊進行成本統計。近似定義每個模塊每年的運營成本為200萬美元，則航天器總運營成本

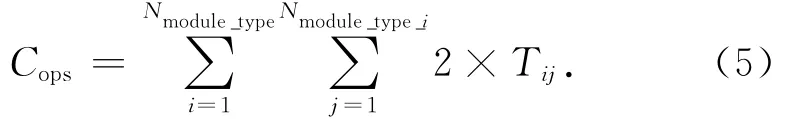
式中：Tij為第i類型第j模塊的在軌運行總時間。

以上兩部分之和即為發射與運營成本。若設計方案能理想實現，整個分離模塊航天器成本即為模塊研制成本和發射與運營成本之和。但實際的空間環境和技術因素等不能保證方案的理想實現，因此整個航天器成本還包括不確定性部分。由不確定性因素而引發的成本不確定項定義為風險成本。

c）風險成本

航天器研制、發射和在軌運行過程中存在各種不確定性因素，導致的任務延期、發射失敗、在軌故障等問題均需要成本投入以保證航天器的正常在軌運行。因此，考慮將這些不確定性因素帶來的風險轉化為以資金度量的風險成本Crisk，以此衡量設計方案的穩健性和可靠性。本文主要考慮發射失敗和在軌故障兩種情況。

一是發射失敗。若發射失敗，則該次發射所攜帶的模塊需重新研制和發射。假設重新發射的模塊和運載器不變，發射失敗的風險成本

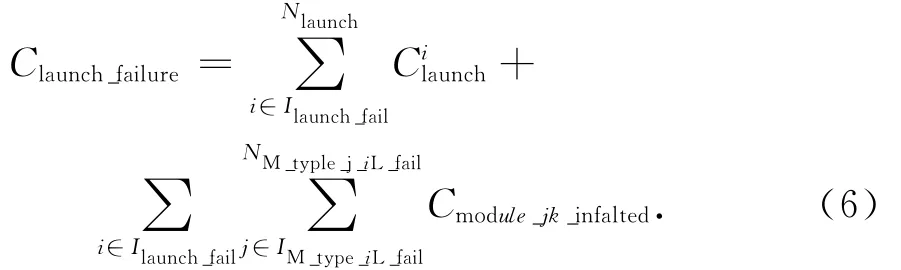
式中：為第i個運載器的發射成本；Ilaunch_fail為發射失敗運載器對應的發射編號；IM_type_iL_fail，NM_type_j－iL_fail分別為發射失敗運載器i攜帶的模塊類型編號及其數量；Cmodule_jk_inflated為第j類中第k個模塊研制成本溢值。

二是在軌故障維修。若分離模塊航天器在軌出現故障，采用發射同型模塊對故障模塊進行在軌更換實現故障維修，則在軌故障維修成本為該新模塊的研制成本與發射成本之和，即

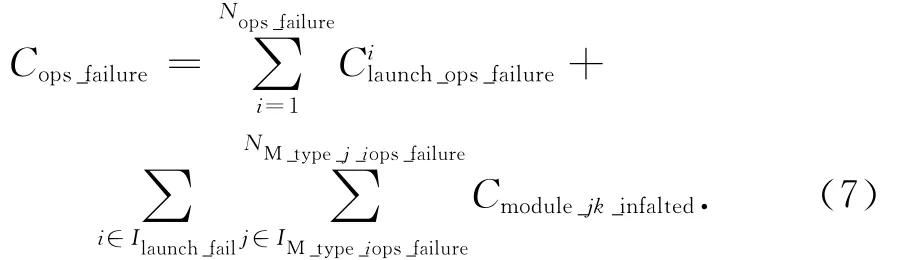
式中：Claunch_ops_failure，Nops_failure分別為在軌運行故障模塊更換所需發射成本和次數；IM_type_iops_failure，NM_type_j－iops_failure分別為在軌故障模塊類型編號及其對應故障模塊數量。

則有

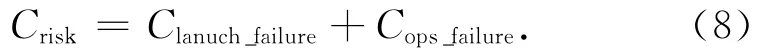
綜上所述，分離模塊航天器總成本為模塊研制成本、發射與運營成本和風險成本的總和。

2.2.2 價值模型

收益模型是衡量航天器價值收益的標準。分離模塊航天器因模塊多，攜帶載荷的功能和工作方式不同，所屬的通信方式也各異。價值模型應將載荷產生的價值趨于一個可衡量的統一量，最終換算成貨幣量的形式。

航天器的任務都需要根據通信鏈路傳輸到地面，所有載荷工作產生的價值均以數據形式表示。在航天器的價值模型中，對數據采取不同的加權因子而進行價值貨幣化。不同載荷對數據的敏感程度和獲取量不同，同時數據的重要性也不同。目標任務重要的數據加權時應取較大的加權因子，反之，則應使用較小的加權因子。

通信鏈路的有效性對價值模型也有影響。航天器設計中常存在多種通信鏈路，每種鏈路的通信的速率和有效率不同，相同的載荷通過不同的鏈路傳輸，得到的價值不同。對數據傳輸的計算主要是基于航天器根據軌道定義計算出的過頂的次數和時間，通過對高速率和低速率空地傳播的有效過頂次數的統計，確定過頂的具體時間值。同時，對各種數傳鏈路的可靠性進行計算從而得到可信數據量，以可信數據量進行價值計算。

若兩個載荷分別采用LR_SG，HR_SG，LR_247三種方式進行數傳，計算價值

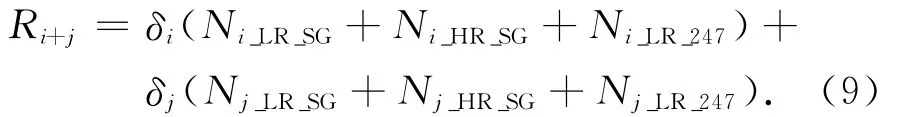
式中：δi，δj分別為載荷i，j的加權因子；Ni_LR_SG，Nj_LR_SG，Ni_HR_SG，Nj_HR_SG，Ni_LR_247，Nj_LR_247分別為載荷i，j通過LR_SG，HR_SG，LR_247數傳方式得到的有效數據量。分離模塊航天器生命周期內價值收益計算流程如圖3所示。

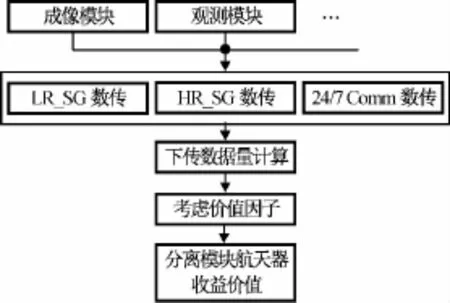
圖3 航天器價值計算流程Fig.3 Estimation procedure of value during life

2.2.3 不確定性模型

以價值為中心的航天器設計方法中，除受模型精確度的影響外，影響成本與價值評估的準確度主要是確定性因素。不確定性模型建立的準確度和全面性對成本與價值評估的準確度產生重大影響。在航天器的生命周期內，不確定性因素時時對航天器產生影響。主要影響可分為對成本模型的影響和發射運營的影響。

成本模型的不確定因素分布在模塊成本、發射成本和操控成本中，根據經驗和技術成熟度TRL設定不確定性因子的上界和下界。同時利用與成本和價值水平相關的參數進行不確定性成本的計算，如離散率、學習曲線率、發射運載學習曲線率、保險成本因子、通貨膨脹率、年平均操作成本等。

三角形分布是工程項目成本風險理論中最廣泛應用的模型。通過三角形分布可從中預測最大、最小和最可能的值，靠近最大、最小值的值出現的可能性小于靠近最可能值的值。各種不確定性的概率分布不同，但通過三角形分布可較準確地對各種不確定性進行研究。本文用三角形分布對不確定性進行建模，以成本不確定性為例進行研究。設成本上限和下限分別為Cmax，Cmin，標準期望成本為Cs，判定因子A＝（Cs－Cmin）／（Cmax－Cmin）。用隨機變量p進行隨機判定：若p≤A，則

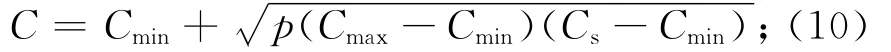
若p＞A，則

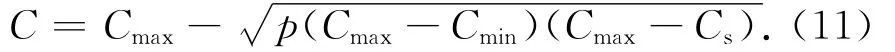
不確定模型對發射運營階段的航天器的影響主要體現在發射是否成功、模塊是否出現在軌故障等，這些均會對成本與價值產生影響。發射成功與失敗的不確定性模型依賴于發射運載器的可靠性，而模塊在軌故障的不確定性模型依賴于模塊的可靠性。

以上不確定性模型均將不確定性因素作為隨機變量，利用概率論中的事件概率處理方法對相應的成本與價值進行核算。

3 成本與價值評估流程

實現分離模塊航天器的成本與價值評估需按航天器生命周期的時間歷程。航天器的生命周期大致分為模塊設計與研制、發射運載、在軌調試與運營三個階段，每個階段內分別對成本與價值進行核算，最終在航天器生命周期截止時得到總體的成本與價值。評估流程如圖4所示。

在設計的初始化階段主要是對相關參數的定義賦值，由用戶選擇航天器任務設計過程中需考慮的不確定性因素，用戶自行選擇功能組件進行組裝成模塊及模塊的發射運載。相關參數的賦值包括對分離模塊航天器飛行環境參數定義和模塊物理參數、衛星平臺、數傳特性等參數的設置。模塊研制和發射日程表的變化、發射失敗、在軌失敗等不確定性因素由用戶自行設置。在對地觀測載荷、高帶寬通信組件等功能性組件滿足組件組合約束的條件下，用戶根據任務內容設計。

設計階段的成本按需求對不確定性因素選取、通貨膨脹率等進行計算匯總。按航天器在此階段所耗費的成本進行累加。若考慮模塊研制時間延遲等不確定性因素，則應根據通貨膨脹率、延遲時間等計算風險成本。由于此階段的航天器并未在軌，不能創造價值，不考慮價值。

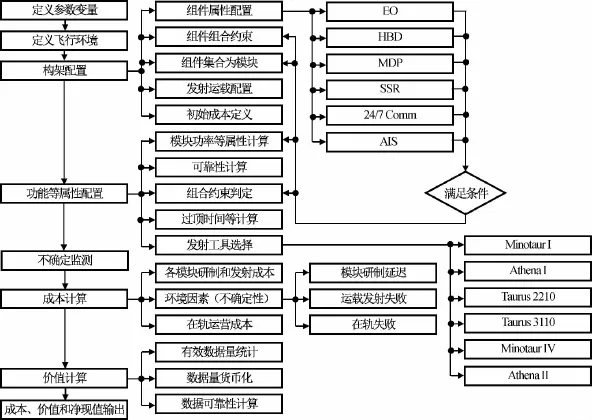
圖4 分離模塊航天器成本與價值評估流程Fig.4 Estimation procedure of value and cost during life

航天器的不同模塊按用戶設計方案依次進行發射。若發射方案中不考慮不確定性因素，則僅計算發射運載成本。如用戶選擇考慮發射失敗、發射延遲等不確定性因素，成本計算應包括風險成本。由于發射運載成本巨大，用戶在設計模塊組合發射時應考慮發射運載器的可靠性和模塊的研制成本，將發射失敗后所耗費的風險成本降至最低。發射階段由于模塊還未進行正常運作，未產生價值收益，故收益為零。

在軌調試部分的持續時間為1個月，可與在軌操控階段聯合計算。從在軌操控部分開始，模塊的功能組件能開始在軌運作，能產生價值收益。不同功能組件產生的不同技術收益均通過數傳方式獲取。數據量大小可衡量收益多少。但不同功能組件的技術收益的實際利用價值不同，在計算價值收益的過程中除考慮數傳方式不確定性外，還要加入價值因子，將不同功能組件的收益根據利用價值的效率價值化。

成本與價值收益在此階段均受不確定性因素的影響。模塊在軌運行受到不確定因素影響、模塊壽命到期等可能會使模塊功能失效，若用戶選擇模塊替換，則將替換模塊的研制成本和替換模塊的發射運載成本作為風險成本加到航天器的總成本中。在此替換期間，失效模塊不產生價值，價值收益應停止計算。

分離模塊航天器的成本和價值收益按此流程計算，直至航天器生命周期終止。根據得到的成本與價值收益，考慮生命周期的時間項得出評估指標NPV的值。

4 基于遺傳算法確定性多學科優化

價值導向的評估方法可自定義輸出多種目標結果，包括平均成本的期望值和方差、平均收益的期望值和方差、凈現值等，導致優化過程本質是求解Pareto意義下多目標最優問題。在具體操作過程中，需針對不同目標結果的權重系數，比較優化結果連續性（剔除突變的設計結果）。

用通用優化平臺的確定性多學科優化問題，無法甄別對優化過程影響微弱的參數，將蒙特卡羅仿真轉化為優化迭代，導致搜索效率下降。迭代過程的本質是各種情況的并行比較，本文考慮搜索效率和平臺實用性，用遺傳算法作為計算平臺對分離模塊航天器進行參數優化。

VCDM工具的最終目的就是在精確建立的航天器平臺及各模塊的模型、不確定性模型，通過遺傳算法的初始化、個體評價、選擇運算、交叉運算、變異運算直至滿足終止條件，最終獲得好的成本與價值關系。分離模塊航天器的評估并非絕對評估計算，而是相對比較并為分離模塊航天器設計方案提供參數優化根據。通過航天器系統成本與價值的評估，確定主要影響因素，通過調整參數達到航天器系統的最優投入產出比。

在分離模塊航天器系統優化過程中，先對航天器系統進行建模，包括體系結構建模、發射運載方案設計、成本價值和不確定性建模。其次，確定優化目標和優化參數。優化目標根據航天器任務要求而具體確定，若要求航天器經濟穩定性好，則應將任務的優化目標設置為NPV方差最小；若要求航天器投入產出比最高，則將任務的優化目標設置為NPV均值最大。之后，用遺傳算法尋找最優方案。分離模塊航天器優化設計流程如圖5所示。

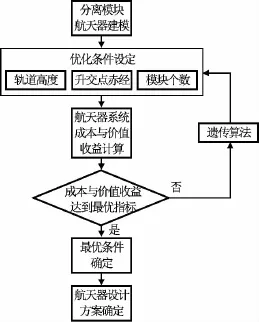
圖5 優化設計方法流程Fig.5 Optimization procedure of NPV during life

5 實例仿真

分離模塊航天器的系統評估和優化設計均按航天器的生命周期歷程進行，通過對整個生命周期內航天器的模塊研制、發射與運營等階段的成本與價值核算得到系統評估值，用戶根據任務確定優化目標，通過遺傳算法平臺得到分離模塊航天器的優化參數。

5.1 系統評估

取航天器軌道高度500km，降交點地方時為上午10：30，軌道為太陽同步軌道。航天器設計研究任務在1月份開始，模塊的設計時間為2年，生命周期為5，10年。可分離組件6個，其相關參數見表1。表中：FIT為1 000h內失敗次數，是表征組件可靠性的參數。

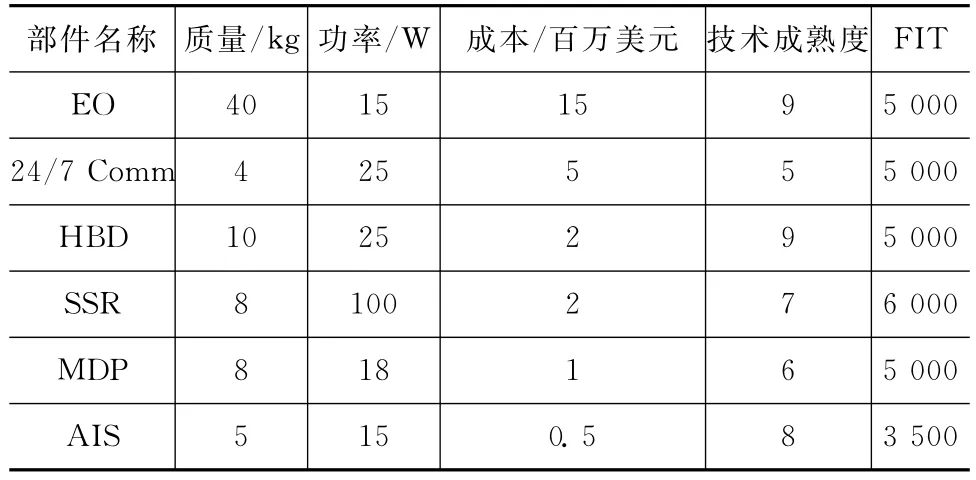
表1 可分離部件性能和參數設置Tab.1 Parameters of separable components

考慮成本不確定性、日程表變化、發射失敗、在軌故障失敗、商業保險、模塊替換等因素，得NPV見表2、3。兩種生命周期的航天器的成本與價值計算結果見表4、5。

分別將置信水平設置為0.5，0.68，用蒙特卡羅方法所得兩種生命周期的航天器的成本和收益分別如圖6、7所示。

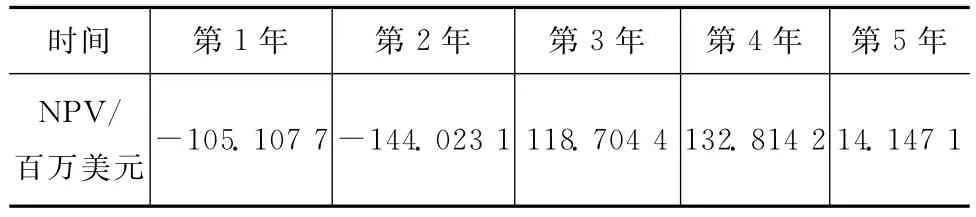
表2 5年生命周期航天器的凈現值NPVTab.2 History of NPV during 5years

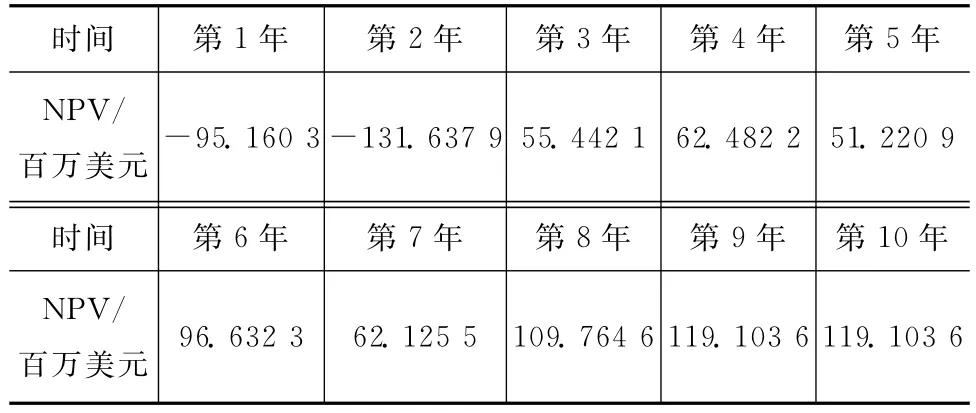
表3 10年生命周期航天器的凈現值NPVTab.3 History of NPV during 10years

生命周期不同，成本和價值就會不同。生命周期長，在軌操控成本、模塊替換成本等會相應增加，同時創造的價值也會增加。因此，航天器生命周期10年的成本和價值與5年的相比較會有較大的增大。

表4 5年生命周期航天器的平均成本與收益Tab.4 Cost and value of fractionated spacecraft during 5years

表5 10年生命周期航天器的平均成本與收益Tab.5 Cost and value of fractionated spacecraft during 10years

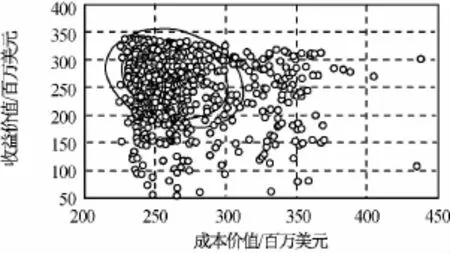
圖6 航天器成本與價值分布（5年）Fig.6 Ergodic representation of value and cost for fractionated spacecraft during 5years

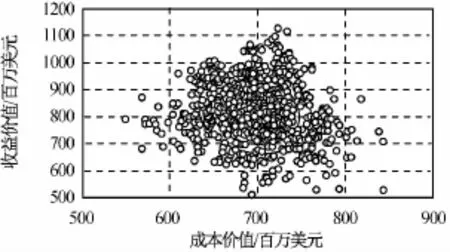
圖7 航天器成本與價值分布（10年）Fig.7 Ergodic representation of value and cost for fractionated spacecraft during 10years

NPV值是多種不確定性因素共同作用的結果，與分離模塊航天器的生命周期長短無關系。遠離置信區間的點是多種不確定因素同時發生的結果，在實際工程實踐中可能性極小，評估中不予考慮。

分離模塊航天器不同模塊數的NPV值如圖8所示。整體航天器在初期階段的投入產出比優勢較顯著，隨著時間延長，分離模塊航天器的投入產出比越來越高。這與F6項目中對分離模塊航天器的技術論證相符。

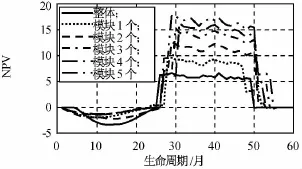
圖8 不同模塊數航天器凈現值NPV分布Fig.8 NPV of spacecraft with various number of fractionated modules

5.2 航天器系統優化設計

對生命周期5年的分離模塊航天器進行優化，優化變量為軌道高度、降交點地方時和模塊數，各自的約束邊界分別為［400，700］km，［9，13］h，［1，6］。遺傳算法參數為：進化代數50，每代種群數100。以最大化NPV均值為目標，所得優化結果如圖9所示：軌道高度573.715km，降交點地方時11.237，模塊6個。以最小化NPV的標準差作為目標，所得優化結果如圖10所示：軌道高度598.939 6km，降交點地方時11.32，模塊數1個。

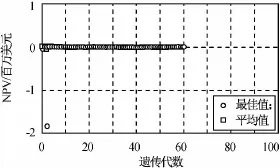
圖9 以NPV均值為目標的優化結果Fig.9 Optimal scheme refined by mean of NPVs

系統優化設計初始化的尋優條件中設置的模塊數為1～6，尋優過程中遺傳算法根據優化目標要求對模塊數及軌道高度和降交點地方時進行尋優以獲取更好的優化目標。以NPV均值最大為優化目標所得結果表明：分離模塊航天器的投入產出比高于整體航天器，在此模型專中模塊個數為6時，航天器獲取最高的凈現值。系統優化設計的優化目標不同，所得優化結果也不同。若保持航天器模型和尋優條件不變，以NPV的標準差最小為優化目標，則模塊為1的航天器最優，即整天航天器的穩定性更高，與實際工程實踐相符。

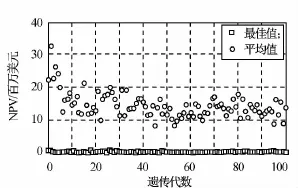
圖10 以NPV方差為目標的優化結果Fig.10 Optimal scheme refined by variance of NPVs

在建立航天器模型基礎上，用戶可根據具體航天器任務設定不同的優化目標，用遺傳算法的優化計算，得到優化目標最優時的優化條件參數。航天器系統的評估目的是對已設計的航天器系統進行成本與價值收益評測，而確定性學科的優化設計則根據用戶的需求為目標，對航天器系統參數進行調整尋優，保證用戶得到更高的投入產出比。

6 結束語

本文用VCDM方法對分離模塊航天器進行設計，建立成本模型、價值模型和不確定性模型。對模塊功能組件按模塊的物理約束、功能約束和用戶需求進行組合設計，在發射運載器承載能力范圍內，設計航天器的模塊組合發射方案。對分離模塊航天器生命周期內的模塊研制、發射運載、在軌操控三個階段的不確定性進行分析，根據三角形概率分布計算航天器的風險成本。統計整個生命周期的成本與價值收益，得到分離模塊航天器的總成本和總價值收益。用蒙特卡羅方法得到不同不確定性因素影響下的航天器總成本和總價值收益并進行分析。基于遺傳算法以NPV為優化目標對分離模塊航天器設計進行確定性學科優化，得到的優化條件可作為航天器設計參數，能達到NPV最大。

分離模塊航天器以其技術性能和經濟優勢受到越來越多重視，以價值為中心的航天器設計方法VCDM能評估航天器的投入產出比，在航天器設計中具有極大的指導意義。對成本與價值評估的確定性學科優化能直接為設計者提供最優的參數值，在未來的航天器設計中將會起到重要的作用。

［1］ BROWN O C，EREMENKO P.Value－centric design methodologies for fractionated spacecraft：Progress summary fromphase1of the DARPA system F6program［R］.AIAA，2009－6540.

［2］ McCORMICK D，BARRETT B，CLAPP－BURNSIDE M.Analyzing fractionated spacecraft architectures using RAFTIMATE－A Boeing tool for valuecentric design［R］.AIAA，2009－6767.

［3］ EICHENBERG B E，WISNIEWSKI M J，CHOI S W，et al.Using a value－centric tool framework to optimize lifecycle cost，value，and risk of spacecraft architecture［R］.AIAA，2009－6765.

［4］ O’NEIL D A，MANKINS J C.The advanced technology lifecycle analysis system （ATLAS）［R］.IAC－04－IAA.3.6.3.01.2004.

［5］ RICHARDS M G，ZOE S，O’NEILL M G，et al.Implementation challenges for respnsive space architectures［R］.AIAA，RS7－2009－2004.

［6］ BROWN O.The value proposition for fractionated space architectures［R］.AIAA，2006－7506.

［7］ BROWN O.Application of value－centric design to space architectures：the case of fractionated spacecraft［R］.AIAA，2008－7869.

［8］ MATHIEU C，WEIGEL A L.Assessing the flexibility provided by fractionated spacecraft［R］.AIAA，2005－6700.

［9］ O’NEILL M G，YUE H，NAG S，et al.Comparing and optimizing the DARPA system F6program valuecentric design methodologies［R］.AIAA，2010－8828.

［10］ LAFLEUR J M，SALEH J H.GT－FAST：apoint design tool for rapid fractionated spacecraft sizing and synthesis［R］.AIAA，2009－6802.

［11］ 劉 豪，粱 巍.美國國防高級研究計劃局F6項目發展研究［J］.航天器工程，2010，19（2）：92－98.

［12］ YAO Wen，CHEN Xiao－qian，ZHAO Yong，et al.A fractionated spacecraft system assessment tool based on lifecycle simulation under uncertainty［J］.Chinese Journal of Aeronautics，2012，25：71－82.