帶有擾動的時滯系統的穩定性分析

盛春紅

沈陽化工大學科亞學院

帶有擾動的時滯系統的穩定性分析

盛春紅

沈陽化工大學科亞學院

采用新的Lyapunov函數方法，獲得了具有非線性擾動的時滯系統穩定性充分條件，引入了新的引理，利用線性矩陣不等式技術（LMI），得到了更好的保守性結果，數值仿真例子說明了方法的可行性和有效性。

穩定性分析；時變時滯系統；Lyapunov第二方法；線性矩陣不等式(LMI)

引言

時滯現象存在于實際工程系統中，帶有一定程度的時間延遲現象。時滯系統更加的接近于實際系統，例如，各種工業成產環節，傳輸系統等，介于很多實際系統都是非線性的系統，而且復雜度非常大，因此，用精確的數學模型來描述這些由微分方程表達的動態系統是很困難的，進而找到一種既接近于實際工程系統又方便研究的數學微分方程模型就顯得非常有必要，所以研究帶有擾動的時滯系統具有深刻的理論意義和研究價值，破壞系統穩定性的主要根源就是時滯，對系統的分析和綜合帶來很大的影響，現在對帶有擾動的時滯系統的穩定性分析和控制器設計，已經成為現代控制理論的研究熱門。

一、系統描述

考慮如下時滯系統：

非線性項滿足如下條件：

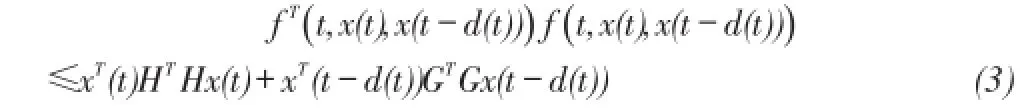
其中，G,H為給定的常值矩陣。

引理1(Liu[1,2])

引理2對任意的實向量a，b和任意適維給定的矩陣Z＞0，有如下矩陣不等式成立：

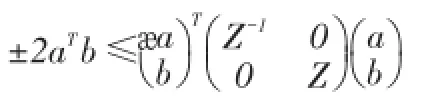
首先，考慮時滯系統(1)：

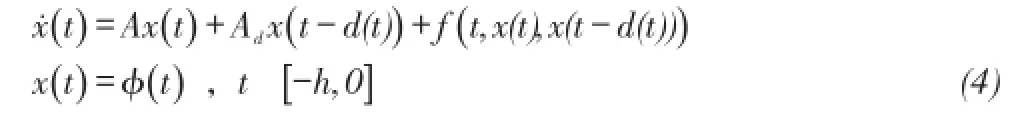
引入如下形式的李雅普諾夫函數(5)，采用線性矩陣不等式(LMI)技術得到系統(4)的漸進穩定的充分條件:

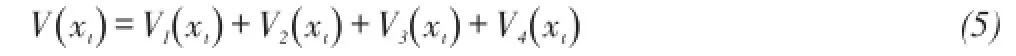
其中：

其中P＞0,Q1＞0,Q2＞0,R1＞0.

二、主要結論

給出時滯系統(1)的穩定性充分條件，得到如下定理。

定理在零輸入的條件下，如果存在標量ε1＞0，及P＞0, Q1＞0,Q2＞0,R1＞0,Z1＞0，Z2＞0，以及適當給定的矩陣H，H2，H3，X11，X12，X13，X22，X23，使得如下線性矩陣不等式(LMI) (7)成立,則時滯系統(1)是漸進穩定的.

其中

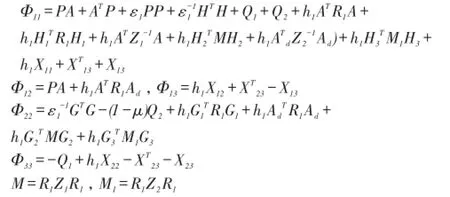
證明選擇形如(6)的Lyapunov函數V(xt).引入系統(1)，對文中所選擇的Lyapunov函數V(xt)(6)求導可得，

由引理2得，

由(8)～(17)，得

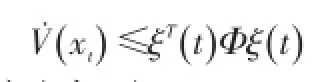
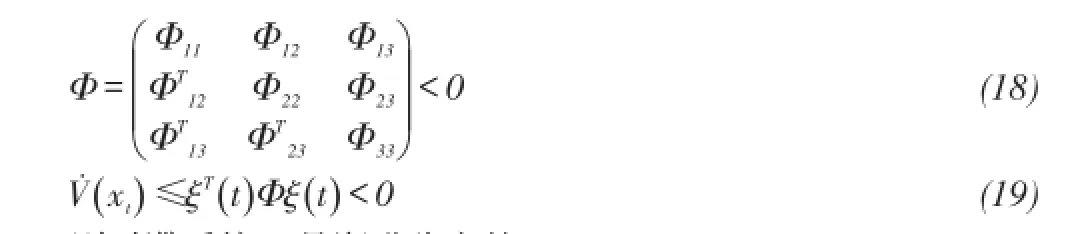
則時滯系統(1)是漸進穩定的。

數值仿真

考慮時滯系統系統(1)，其中

令μ=0.8，根據定理求解式矩陣不等式（LMI）(7)，得h=2.0418。

上述數值仿真結果表明本文定理是正確的，由于采用了新的Lyapunov函數，引入了更多的自由矩陣，增加了解得可行域，從而具有了更好的保守結果。

[1]LiuPL.Furtherimprovementondelay-range-dependentstability?resultsforlinearsystemswithintervaltime-varyingdelays.ISATrans2013. http://dx.doi.org/10.1016/j.isatra.2013.07.006(in press).

[2]LiuPL.Robuststabilityofintervaldynamicsystemswithmultiple?time-delays.Electron Lett2001；37:1269-70.

[3]LiuPL.Statefeedbackstabilizationoftime-varyingdelayuncer?tainsystems:adelaydecompositionapproach.LinearAlgebraAppl2013；438(5):2188-209.

[4]湯紅吉.不確定時滯系統的魯棒控制.2005,4.

[5]張金會,不確定時滯系統的魯棒控制研究.206,12.

[6]LamJ,GaoH,WangC.Stabilityanalysisforcontinuoussystemswith?twoadditivetime-varyingdelaycomponents.SystControlLett2007；56(1): 16-24.

4.2 電除塵參數

從表1數據可以看出，二次電壓最高80KV,最低61KV(額定值80KV)；二次電流接近額定值（一電場二次電流額定為1600mA,二電場二次電流額定為1400mA，三電場二次電流額定為1200mA，四電場二次電流額定為1000mA），設備運行狀態良好、穩定，電除塵出口粉塵濃度排放在運行過程中沒有超標過。