利用草圖培養學生數形結合的思想

秦虹

【關鍵詞】數學草圖 數形結合 思想方法

【中圖分類號】G 【文獻標識碼】A

【文章編號】0450-9889（2015）10A-0089-02

《義務教育數學課程標準（2011年版）》將滲透數學思想方法作為一個明確的教學目標提了出來，要求教師加強教學實踐，發展學生的數學思維，提高學生的數學能力。那么，在實際教學中，如何進行數學思想方法的有效滲透呢？筆者認為，教師應從小學數學的數與形的結合入手，帶領學生感知數學思想方法，提升數學思維。何謂數學思想方法？它是從某些具體的數學認識過程中提煉出的一些觀點，揭示了數學發展中普遍的規律，也是人們對數學理論與內容的本質認識，直接支配著數學的實踐活動，這是對數學規律的理性認識。而數學方法，則是解決數學問題的方法，即解決數學具體問題時所采用的方式、途徑和手段，也可以說是解決數學問題的策略。對于小學數學教學來說，數學思想是宏觀的，它具有普遍的指導意義，而數學方法是微觀的，它是解決數學問題的直接、具體的手段。一般來說，前者給出了解決問題的方向，后者給出了解決問題的方法。但由于小學數學內容比較簡單，所以隱藏的思想和方法很難截然分開，更多反映在聯系方面，其本質往往是一致的。如常用的分類思想和分類方法，集合思想和交集方法，在本質上都是相通的，所以小學數學通常把數學思想和方法看成一個整體概念，即小學數學思想方法。

在小學數學教學中，數和形是數學研究的兩個主要對象，數離不開形，形離不開數，一方面抽象的數學概念、復雜的數量關系，借助圖形使之直觀化、形象化、簡單化；另一方面復雜的形體可以用簡單的數量關系表示，讓學生很容易就找到解決問題的辦法，尤其是在解答應用題時，教師可以引導學生借助線段圖幫助學生分析數量關系，并建立問題鏈接，分析解決問題的路徑，讓學生深刻理解并借助數學思想解決數學問題。

下面筆者就在教學中如何培養學生利用畫草圖，訓練學生數形結合的數學思想方法談一些做法。

一、利用草圖數形結合，學會思考問題

根據小學教材的編排體系不難看出，數和形是數學研究的兩個主要對象，教材中的數是通過形來展現的，由此幫助學生建立直觀形象的概念，理解抽象的數學概念和復雜的數量關系，借助圖形使之直觀化、形象化、簡單化；同時，能夠讓學生借助簡單的圖形，將復雜的問題直觀呈現，以此采用簡單的數量關系圖，梳理問題中的解決路徑。數形結合的思想方法的本質，就是讓學生將數（量）與（圖）形結合起來進行分析、研究，最終找到解決問題的辦法的一種思維策略。教學時，教師可以引導學生在解應用題中，借助線段圖的直觀幫助分析數量關系。

學生在高年級時通常會遇到一些較復雜的題目，如“在200米的路的一旁，每隔5米栽一棵樹（兩端都栽），一共需要栽多少棵樹？”教學時，教師可組織學生思考：“我們可以先利用畫圖的方法找找路和樹之間有什么關系？可以動手畫一畫，想一想，等理清楚了路和樹之間的關系，你就找到了解決這道題的辦法。”

學生在動手畫圖后很容易找出路和樹之間的關系：

經過觀察和比較，學生發現圖二、圖三不屬于兩端都栽，而圖一中樹的棵數比路分成的段數多1，再把路分成三段、四段……

學生從上面的圖中可以歸納出：兩端都栽，樹的棵數=路的段數+1。再讓學生利用同樣的方法尋找圖二、圖三中的規律。學生會借助圖形的幫助很快得出：兩端都不栽，樹的棵數=路的段數-1；一端栽一端不栽，樹的棵數=路的段數。

這樣，學生理清了路和樹之間的關系，他們很快列出算式200÷5+1=41（棵）。

以上教學，教師從直觀的畫圖入手，讓學生看到數量關系的變化，并從中感受到“兩端都栽、兩端都不栽、一端栽”三種形式，從而理清了三種情況下的解決問題路徑，建立了數形結合的思維意識。

二、利用草圖數形結合，學會轉換數量關系

數量關系的轉換是小學數學教學的一個難點。學生受到慣性思維模式的影響，容易迷失方向，在解題時不知道該怎么解。例如，教學分數乘除法應用題時，學生常常找不到單位“1”，不知道何時該用乘法，何時該用除法。有基于此，筆者將草圖作為一個重要的教學策略，引導學生利用線段圖進行有效分析，讓學生能夠自主畫出線段圖，使其直觀地呈現出數量與分率之間的關系，特別體現在一些需要轉換單位“1”的題目中。

例如，“兄弟四人合作修一條路，結果老大修了另外三兄弟總數的一半，老二修了另外三兄弟總數的，老三修了另外三兄弟總數的，老四修了91米，問這條路長多少米？”學生一開始不知道如何梳理三者的關系，對另外三個人的關系的理解存在誤區。為此，筆者帶領學生展開探究：請你畫出一幅線段圖，展示老大和另三人的份數。學生由此通過畫圖展示老大是另三人的一半，通過畫圖呈現：（如圖）

通過這樣直觀呈現，將數與形有機地結合在一起，學生能直觀發現：老大占總數的，也就是總數的。基于這樣的引導，學生繼續按照同樣的思路畫圖，馬上能找出老二占總數的，老三占總數的，再次通過畫圖呈現出總數與部分之間的關系，即91米對應的分率是1---，很快問題就解決了。

三、利用草圖數形結合，培養學生空間想象力

新課標將空間能力的培養列為重點內容，要求教師進行直觀引導，幫助學生建構空間概念，發展空間想象力。在實際教學中，筆者發現，通過利用草圖，能夠將一些較為復雜的立體圖形進行分解，有助于培養學生的空間想象力，幫助學生解決一些復雜的數學圖形題。例如：

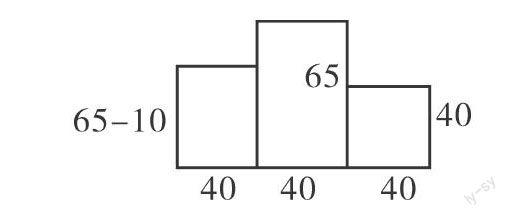
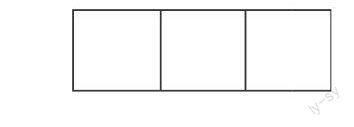
這道題的難點，是要有一個立體的空間感受，然后分析問題，找到解決問題的辦法。因而，在思考這道題時，教師要引導學生從幾個方面探究，將其分成前、后、上、下、左、右六個方向展開觀察，并將觀察到的圖形畫出來，找到相應的條件，就能算出這個頒獎臺涂紅油漆和黃油漆的面積分別是多少了。學生一邊畫圖一邊思考：涂紅油漆的是哪一面？從上面計算是多少？如果從左面是多少呢？右面呢？學生從上面觀察：發現上面是由三個正方形組成的長方形，畫出來，得到一個平面圖形，由此可以得到面積為40×40×3=4800（平方厘米）。

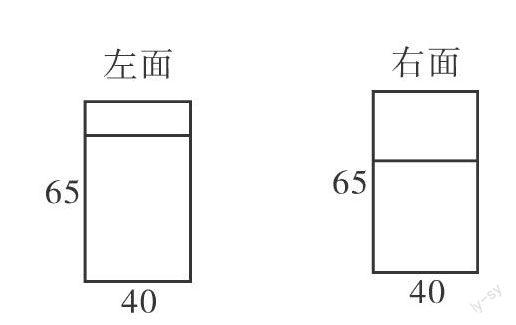
學生再從左面、右面分別觀察，發現左面和右面是兩個一樣的個長方形，畫出來，得到一個平面圖形，通過平面圖可以得到面積為65×40×2=5200（平方厘米）。

根據以上觀察到的圖形，學生很快得到計算結果：涂紅油漆的面積為4800+5200=10000（平方厘米）。涂黃油漆的是前面和后面。從前面和后面觀察：前面和后面都是由三個長方形組成，畫出來，得到一個平面圖形（如下圖）。

面積為[（65-10）×40+65×40+40×40]×2=12800（平方厘米）。就這樣，這個復雜的數學習題，通過畫圖，學生有條不紊地展開直觀分析，有效地解決了問題。

總之，在小學數學教學中，教師通過引導，帶領學生利用畫草圖解決數學問題，這樣就可以培養學生的數感，建構解決問題的策略，幫助學生思考，同時也有助于培養學生良好的思維習慣。

（責編 林 劍）