基于熵權五元聯系數在實驗室安全管理評價中的應用

李 焓， 姚 佳

(成都理工大學 教務處，四川 成都610059)

0 引 言

近年來，隨著我國高等教育事業的蓬勃發展，高校實驗室的種類和數量不斷增多，實驗室的教學、科研活動日趨頻繁，實驗室的人員集中度和流動性也相應增加，實驗室安全事故時有發生［1］，因此，加強高校實驗室安管理，提高實驗室安全監管能力，是各高校全乃至整個社會值得深入研究和探討的重要研究課題［2］。實驗室安全管理綜合評價是實驗室建設與管理的一個重要內容［3］。在對實驗室進行安全管理評價時，所涉及到的指標項較多，并且其等級標準存在模糊性，不確定性，使得在數據處理時都存在一些不確定性問題［4］。

集對分析是趙克勤于1989 年首次提出的，是一種研究不確定性的數學方法，在分析處理多目標不確定性問題時具有較強的適用性［5］。基于熵權的五元聯系數集對模型是在集對分析理論和熵權法的基礎上提出的一種綜合評價方法，它從多目標之間的聯系度與轉化的同一度、差異度和對立度描述各個目標之間的相關性，并通過信息熵確定指標權重，進而進行客觀評價［6］。本文試圖將基于熵權的五元聯系數集對模型引入到實驗室安全管理展開綜合評價中，并通過運用實例進行了分析。結果表明，該方法是一種有效的、可靠的評價方法。

1 五元聯系數評價模型

1.1 五元聯系數評價模型

在實驗室安全管理評價時，把實際考評結果作為集合A，考評等級標準看作集合B，通過比較A 集合和B 集合，找出它們同、異、反的聯系度，就可以對各實驗室安生管理進行比較分析，從而判斷所屬等級。

根據上面的思想，現對實驗室安全管理五元聯系數集對模型進行構建。

(1)構建集對H(Al，Bk)。選擇具有代表的評價指標，將樣本評價指標的實測值xl(l =1，2，…，m，m為評價指標數)看成一個集合Al，將相應的標準計為另一集合Bk(k =1，2，…，n;n 為評價等級)，其集合Al，Bk構成集對H(Al，Bk)。

(2)構造五元聯系數。有五元聯系數μAl～Bk描述集對H(Al，Bk)的關系:

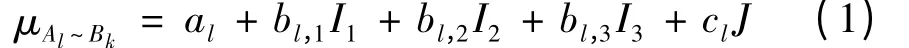
式中，al、bl，1、bl，2、bl，3、cl分別表示指標xl與該指標的Ⅰ級、Ⅱ級、Ⅲ級、Ⅳ級、Ⅴ級標準的聯系度。

(3)構造聯系度表達式。在評價指標體系中將其等級劃分為5 個等級時，將涉及到4 個等級邊界值，因為邊界值具有模糊性，所以若單因子評價落入該級的范圍視為同一，落入相鄰的等級視為差異，落入相隔的等級范圍視為對立，即通過差異度分量解決等級邊界模糊性的問題［7］。由于在實驗室安全管理中所涉及的指標都是效益性的指標(即越大越好型指標)，所以本文采用效益型的聯系度表達式［8］:

式中，s1、s2、s3、s4為評價指標的門限值。

1.2 熵權法確定指標權重

熵權法是一種在綜合考慮各因素所提供信息量的基礎上，計算一個綜合指標的數學方法［9］，它主要是根據各指標傳遞給決策者的信息量大小來確定其權數。因此可以用信息熵評價所獲系統信息的有序度及效用，即由評價指標值構成的判斷矩陣來確定指標權重，其具體計算步驟如下:

(1)根據標準化矩陣計算第i 項指標的熵值ei:

式中，zij(i=1，2，…，n;j =1，2，…，m)為第j 個評價指標的第j 個評價對象具體量值xij進行標準化處理后的結果，k 的取值為:k=，且有0 ＜ei＜1。

(2)計算第i 個指標的差異性系數gi

(3)對差異性系數進行歸一化處理

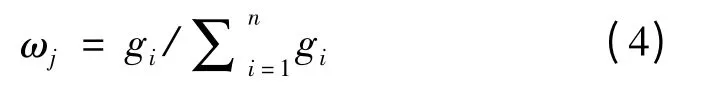
得到熵權權重向量ω=(ω1，ω2，…，ωn)。

1.3 綜合關聯度及評價等級

(1)通過聯系度表達式計算出各指標的聯系度μAl～Bk，再結合各評價指標的權重，計算出綜合聯系度。

式中:ωl為第l 個指標的權重。

(2)等級判定。采用置信度準則來確定其評價等級。

式中:f1，f2，…，fK，為聯系度分量，其參數的意義理解為f1為隸屬于1 級標準的可能程度;f2為隸屬于2 級標準的可能程度;fK為隸屬于K 級標準的可能程度［10］;λ 為置信度，范圍為［0.5，0.7］，對于給定的λ，當hK＞λ 且hK－1≤λ 時，則評價結果屬于級。

2 實例分析

為了驗證該模型在實驗室安全管理綜合評價中的有效性，筆者在現有實驗室管理評價體系的研究基礎上［11-16］，依據科學性、針對性和可操作性的原則，設計出本次實驗室安全管理的評價體系，該指標體系包含21 個指標項，各指標具體內容見表1。

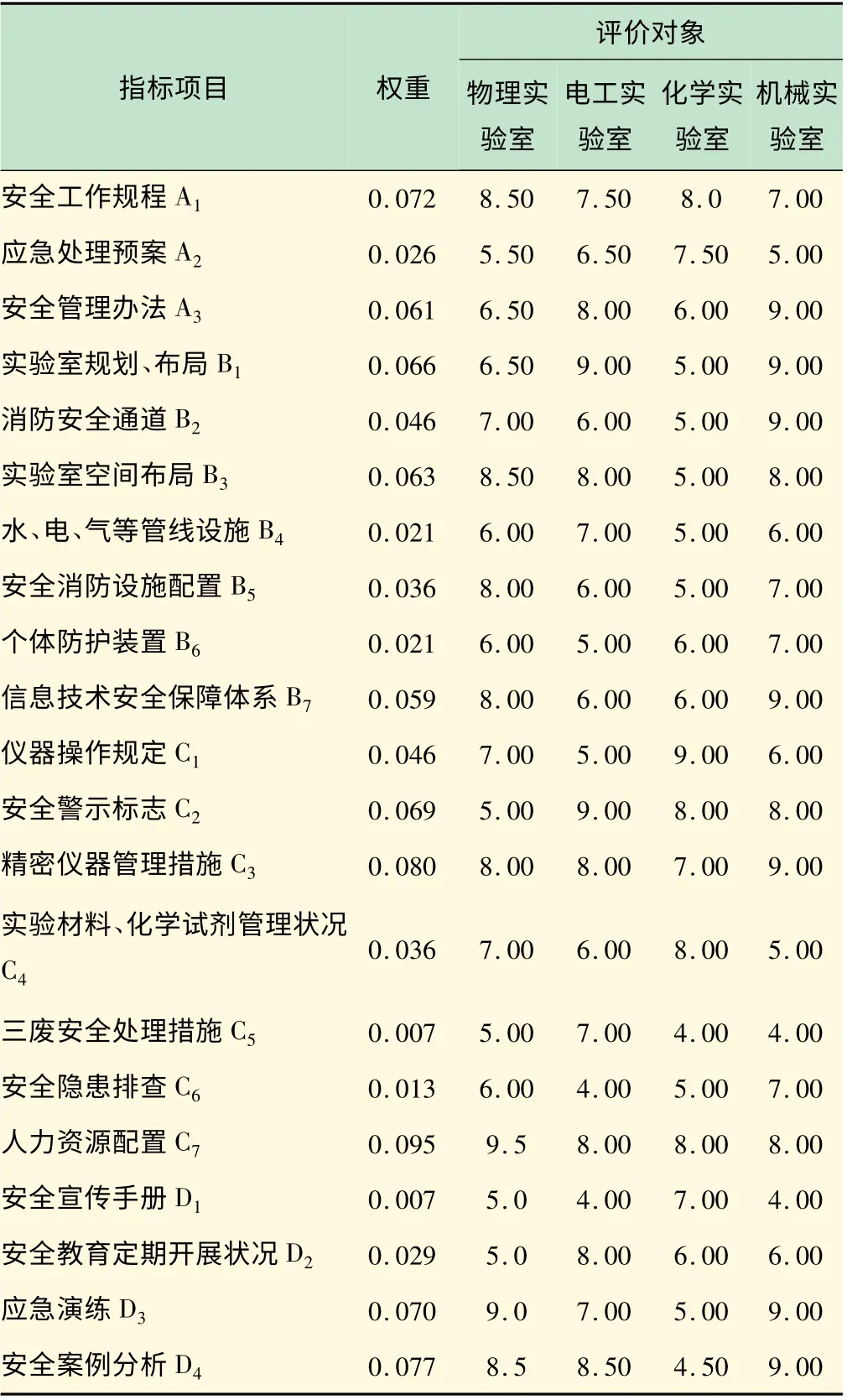
表1 2013 學年某高校教學實驗室安全管理綜合指標

利用該指標體系，分別選取“物理實驗室”、“電工實驗室”、“化學實驗室”、“機械實驗室”作為評價對象，且各指標項的實測值詳見表1。現利用所建模型進行具體分析如下:

(1)評價等級劃分。在評價之前，首先將實驗室安全管理評價等級劃分為Ⅰ～Ⅴ級五個評價等級，五個等級的單因素評價標準臨界值s1，s2，s3，s4，構成5個區間(∞，8］，(8，6］，(6，4］，(4，2］，(2，－∞)，每個區間分別對應“高”(Ⅰ級)、“較高”(Ⅱ級)、“中等”(Ⅲ級)、“較低”(Ⅳ級)、“低”(Ⅴ級)5 個等級。

(2)計算聯系度。依據聯系度表達式，根據各指標的實測值計算各指標對應各等級的聯系度分量(詳細計算結果省略)。

(3)指標權重確定。將表2 中各實驗室相應指標實測量值進行標準化處理后，利用熵權法確定其指標權重ω=(ω1，ω2，…，ω21)，得各指標權重值，結果見表1 中的權重列。

(4)計算綜合聯系度。利用式(5)綜合聯系度計算公式μA～B，計算出各實驗室的綜合關聯度量，結果見表2。

(5)結果分析。依據表2 中各實驗室的綜合聯系度μA～B計算結果，根據置信度原則，取λ=0.5，則h1=f1=0.552;h2=f1=0.563，h3=f1+f2=0.516，h4=f1=0.686，得各實驗室評價所屬等級分別為:Ⅰ(高)，Ⅰ(高)，Ⅱ(較高)，Ⅰ(高)。再根據同一等級的不同聯系度值的大小，進一步對其4 個實驗室的安全管理狀況進行綜合排序，結果為:h4＞h2＞h1＞h3。

表2 綜合關聯度計算結果及所屬等級

將該評價結果與模糊綜合評價法的評價結果進行對比(見表3)，兩種評價分析方法所得的結果相吻合。進一步證明了該模型在實驗室安全管理評價的可行性、可靠性。

3 結 語

基于集對理論，建立起高校實驗室安全管理綜合評價的五元聯系數集對模型，從而為高校實驗室安全管理綜合評價找到一種定量分析的新方法。同時將信息論中的熵權理論運用到指標權重計算，有效地減少評價過程中的主觀性，提高了實驗室安全管理綜合評價的客觀性。最后通過實例進行對比分析，進一步證明了利用該模型在實驗室安全管理綜合評價的適用性和可行性，為實驗室安全管理綜合評價提供了新的參考方法。

表3 評價結果比較

［1］ 賈賢龍.高等學校實驗室安全現狀分析與對策［J］. 實驗室研究與探索，2013，30(12):193-195.

［2］ 朱娟蓉.強化高校實驗室安全管理工作的對策［J］. 實驗室研究與探索，2013，32(6):430-433.

［3］ 武曉峰，聞星火.高校實驗室安全工作的分析與思考［J］.實驗室研究與探索，2013，31(8):81-87.

［4］ 陸琳睿，吳伊萍，陳 祺.基于BP 神經網絡的高校實驗室安全評價模型及應用［J］.實驗室研究與探索，2013，32(2):214-218.

［5］ 趙克勤.集對分析及其初步應用［M］.杭州:浙江科學技術出版社，2000.

［6］ 李文賓，姚阿漫.基于熵權的五元聯系數在地下水水質評價中的應用［J］.水資源與水工程學報，2013，24(2):118-120.

［7］ 王文圣，金菊良，丁 晶，等.水資源系統評價新方法集對評價法［J］.中國科學(E 輯:技術科學)，2009，39(9):1529-1534.

［8］ 馮莉莉，高軍省.基于六元聯系數的水質綜合評價模型［J］.灌溉排水學報，2011，30(1):121-124.

［9］ 熊竣熙，薛 晉，趙冬梅. 基于模糊綜合評價的高鐵工程施工質量風險分析［J］.工程管理學報，2012，26(2):42-45.

［10］ 李 焓.基于集對理論的高校實驗室績效評價方法［J］.實驗室研究與探索，2013，32(12):219-221.

［11］ 魯亞敏，王秀君.地方高校實驗室安全分級考核探析［J］.中國現代教育裝備，2010(17):102-106.

［12］ 蔡仕衡，江 琦，胡 馳，等.高校實驗室安全管理體系建設的探討［J］.實驗技術與管理，2012，29(11):203-210.

［13］ 蔡毅飛，薛 來. 化學實驗室環境－安全模糊評價模型的研究［J］.實驗技術與管理，2012，29(7):199-204.

［14］ 劉春柱. 高校實驗室安全現狀與管理對策［J］. 實驗室科學，2006，8(4):89-92.

［15］ 葉秉良，汪進前，李五一，等.高校實驗室安全管理體系構建與實踐［J］.實驗室研究與探索，2011，30(8):419-421.

［16］ 潘 蕾.實驗室安全管理體系的構建與實踐［J］. 實驗室研究與探索，2010，29(12):188-190.