蒙特卡洛模擬法在復雜系統可靠性仿真中的應用研究

【后勤保障與裝備管理】

蒙特卡洛模擬法在復雜系統可靠性仿真中的應用研究

曾暢1，方強2，吳軍1，朱勇猛1，關靜2

(1.華中科技大學 船舶與海洋工程學院，武漢430074；

2.中國艦船研究設計中心，武漢430064)

摘要：針對蒙特卡洛模擬法應用于復雜系統可靠性仿真分析時遇到的仿真收斂速度慢和精度低等缺陷，建立了復雜系統可靠性仿真模型，使用線性同余發生器抽樣產生隨機事件，根據事件對任務的影響來推算系統的任務可靠度，并與數學解析方法計算的結果進行對比；結果顯示，提出的蒙特卡洛模擬法進行復雜系統可靠性仿真分析時所得到的結果誤差在允許范圍內，且收斂效果較好。

關鍵詞：蒙特卡洛；復雜系統；可靠性仿真

作者簡介：曾暢(1989—)，男，碩士研究生，主要從事裝備綜合保障技術研究。

doi:10.11809/scbgxb2015.09.017

中圖分類號：TB114

文章編號：1006-0707(2015)09-0065-04

本文引用格式：曾暢，方強，吳軍，等.蒙特卡洛模擬法在復雜系統可靠性仿真中的應用研究[J].四川兵工學報，2015(9):65-68.

Citationformat:ZENGChang,FANGQiang,WUJun,etal.ResearchonMonteCarloMethodinReliabilitySimulationofComplexSystems[J].JournalofSichuanOrdnance,2015(9):65-68.

ResearchonMonteCarloMethodinReliabilitySimulationof

ComplexSystems

ZENGChang1, FANG Qiang2, WU Jun1, Zhu Yong-meng1, GUAN Jing2

(1.SchoolofNavalArchitectureandOceanEngineering,HuazhongUniversityofScienceand

Technology,Wuhan430074,China； 2.ChinaShipDevelopmentandDesignCenter,Wuhan430064,China)

Abstract:In order to deal with slow convergence and low precision defects of Monte Carlo method applied to analyze the reliability of complex systems, a reliability simulation model of a complex system was built. Then a linear congruential generator was used to generate random sampling events. And then, the task reliability of the system was reduced according to the influence of the events on the task. Comparisons were made between simulated results and mathematical results. It was shown that the Monte Carlo method has higher precision and a well-performed convergence.

Keywords:MonteCarlo;complexsystems;reliabilitysimulation

可靠性是衡量復雜系統性能優劣的關鍵指標之一，對其進行科學地分析與評價，可以為復雜系統的診斷、改進和維修提供支撐，進而降低因系統故障而引起的各類事故風險。目前，復雜系統可靠性分析方法主要有：基于可靠性框圖和故障樹的圖形演繹法、基于概率論和馬爾可夫鏈的數學解析法、基于事件和時間的仿真法[1]。其中，基于可靠性框圖和故障樹的圖形演繹法由于受到NP組合爆炸問題的困擾，往往難以得到滿意的分析結果；基于概率論和馬爾可夫鏈的數學解析法由于其建模與模型求解較困難，影響了其適用范圍；而基于事件和時間的仿真法由于具有應用靈活、直接簡單、且易于編程實現等特點，尤其適用于圖形演繹法和解析法等難以解決的大型復雜系統可靠性仿真問題，特別是隨著計算機信息處理能力的大幅提升，仿真法逐漸成為大型復雜系統可靠性分析的有效手段[2-5]。

蒙特卡洛模擬法是一種基于隨機變量的統計試驗或隨機模擬方法，它以大數定理為理論基礎，以隨機數為基本工具，能夠處理包含不同壽命分布與可靠性模型的復雜系統可靠性分析問題，且能夠反映出系統故障的隨機性，因而被廣泛應用于可靠性仿真領域[6]。然而，蒙特卡洛模擬法存在收斂速度慢和仿真精度低等缺陷，前人進行了大量研究來提高仿真收斂速度[7]，而對仿真精度的驗證研究較少。為了驗證蒙特卡洛模擬法在復雜系統可靠性分析中的仿真結果是否真實可靠，本文采用蒙特卡洛方法模擬復雜系統執行使命任務過程，并將其可靠性仿真結果與解析法計算結果進行對比。

1復雜系統可靠性分析模型

復雜系統是由眾多的分系統、組件和元件按一定方式構成的。由于系統組成結構的龐大，各元件壽命與維修分布及數據形式的多樣性，使得復雜系統可靠性分析極為繁瑣[8]。可靠性分析模型是分析復雜系統可靠性最有效手段，為此首先建立了某一復雜系統可靠性分析模型[9]。如圖1所示，該系統是由眾多單元通過串聯、并聯、旁聯和冷儲備等邏輯形式組成。每個單元即可以表示元件，也可以表示組件或者分系統。A表示串聯單元，B表示并聯單元，C表示冷儲備單元，D表示n中取k表決單元，其中i、j、m和n為非負整數。分析系統可靠性時，從元件可靠性分析出發，依據系統可靠性分析模型，自下而上依次分析組件、分系統和整個系統的可靠性。

圖1　復雜系統可靠性分析模型示例

對于圖1所示的復雜系統，設串聯單元、并聯單元、冷儲備單元和表決單元的可靠度分別為RA(t)、RB(t)、RC(t)、RD(t)，則整個系統的可靠度R(t)為

R(t)=RA(t)·RB(t)·RC(t)·RD(t)

若已知系統組成元件的可靠性參數(如失效分布和失效率等)，則可以求出每個元件的可靠度，進而根據系統組成單元的邏輯關系，可以推算出系統的可靠度。由此可見，即使在對冷儲備系統進行簡化的情況下，利用數學方法對復雜系統進行可靠性分析依然十分繁雜。為此，本文將運用蒙特卡洛模擬法對復雜系統進行可靠性分析。

2基于蒙特卡洛模擬法的復雜系統可靠性仿真

復雜系統可靠性仿真的分析對象是一類典型的離散事件系統。離散事件系統是指系統狀態僅在離散時間點上發生變化的系統，引起系統狀態變化的行為稱為“事件”，這類系統是由事件驅動的；事件往往發生在隨機時間點上，故稱其為隨機事件[10]。其中，事件包括故障事件和維修事件，即單元運行過程中發生的故障現象與相對應的維修活動，時間包括單元發生故障的時間及其維修消耗的時間。基于蒙特卡洛模擬法的復雜系統可靠性仿真基本原理是模擬系統運行時產生的故障事件和維修事件，系統組成元件的故障及其維修活動將會直接或間接地影響到系統的正常運行，依據這些事件對系統的影響來統計分析系統可靠性水平。如前所述，蒙特卡洛模擬法是一種應用隨機數來進行計算機模擬的方法，此方法使用隨機數發生器對系統進行隨機抽樣，通過對樣本值的統計，求得待研究系統的某些參數[11]。若已知設備單元的壽命分布和維修分布的類型與參數，便可抽樣產生相應的隨機事件，具體方法如下：

假設系統某一組成單元的可靠性分布類型為指數分布，R(t)=exp(-λt)，其中λ為故障率。采用直接抽樣方法，可以得到系統在執行某一任務期間該組成單元發生故障的一組時間序列，即

其中，N表示總的仿真次數，Ti表示第次抽樣時所得的故障時刻，ηi表示在[0,1]區間上均勻分布的隨機數。ηi是由線性同余發生器產生的，其遞推公式為

其中：xi為產生的偽隨機數；x0為初值；m為模數；a為乘數；c為增量；且xa，m，a和c皆為非負整數。

通過上述方法，可以抽樣得到系統的故障事件和維修事件，再經過大量的隨機抽樣得到仿真所需要的事件集合，稱為隨機事件表，由此對系統進行可靠性分析，具體步驟如下：

步驟1：選擇合適的隨機數發生器，基于單元的故障與維修分布，利用隨機數抽樣得到單元的故障事件和維修事件。在系統任務時間內，按照故障發生時間和優先級排列事件，構成可靠性分析所需要的故障事件表和維修事件表；

步驟2：從初始化的系統時鐘開始，掃描處理故障事件表和維修事件表。根據單元與任務的邏輯關系，判斷其發生故障和實施維修是否會引起任務失敗，在單元執行任務期間，若其累計失效時間超過預設值，則任務失敗；

步驟3：記錄每一次仿真的結果，進行N次仿真時，若任務失敗次數為F，則系統的任務可靠度近似值為R=1-F/N；為保證仿真精度，N至少取2 000次。

3實例分析

為驗證運用蒙特卡洛模擬法進行系統可靠性仿真的可行性，以某型艦船電氣系統為對象分析其在1年內(約8 640h)執行巡航任務的可靠性。首先，通過分析該系統的組成結構、功能原理和任務剖面等，建立圖2所示的系統可靠性分析模型。

圖2　某型艦船電氣系統可靠性分析模型

在調研和查閱資料基礎上，得到表1所示的系統組成單元的可靠性和維修性分布類型及其參數等。需要指出：指數分布雖然不能作為機械零件功能參數的分布規律，但是它可以近似地作為高可靠性的復雜部件、機器或系統的失效分布模型，已經在部件或機器的整機試驗中得到廣泛的應用。為此，假定系統組成單元的可靠性與維修性分布皆為指數分布。

表1　單元的可靠性和維修性分布函數及參數

采用數學解析法推算該系統的任務可靠度。如圖2所示，整個系統是由4個分系統串聯而成，即冷儲備系統(發電機組)、串聯系統(變壓器和電氣控制裝置)、并聯系統(分電箱)和表決系統(電機)。設4個分系統的可靠度分別為R1(t)、R2(t)、R3(t)和R4(t)。根據各組成單元的可靠性分布及參數，結合系統可靠性分析模型，推算出整個系統的任務可靠度為

R(8 640)=R1(8 640)R2(8 640)R3(8 640)R4(8 640)=0.942 9×0.617 8×0.665 3×0.376 8=0.146 1

采用蒙特卡洛模擬法來推算該系統的任務可靠度。設置仿真次數N為5 000，選擇線性同余發生器產生隨機數，得到系統的故障事件與維修事件，經系統仿真，計算出系統任務可靠度，如圖3所示。

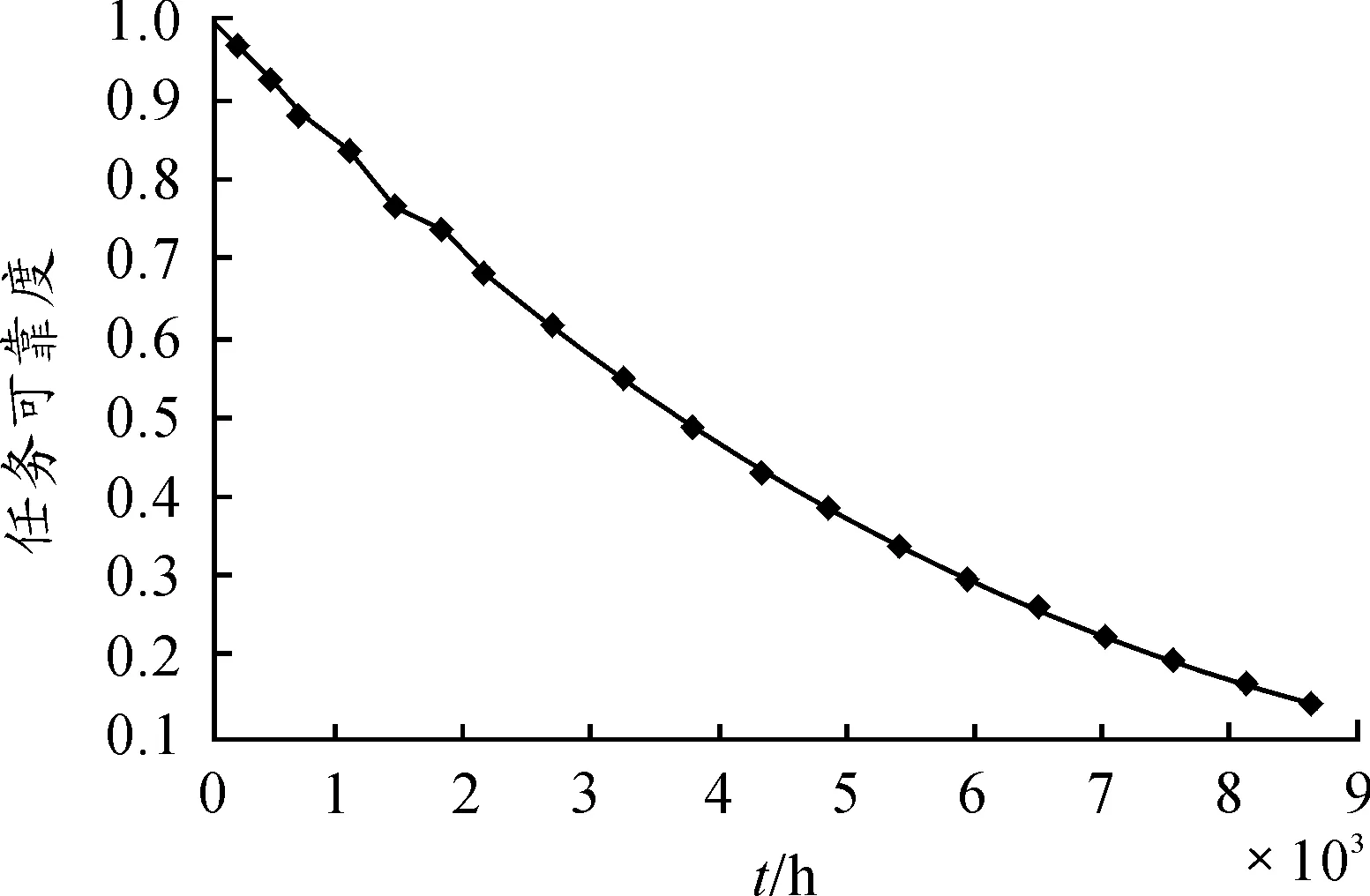
圖3　任務可靠度隨時間的變化趨勢

選取該系統任務期間內的6個時間點進行分析，采用仿真法計算得到任務可靠度，并與數學解析法得到的任務可靠度進行對比，對比結果如表2所示。由此可見，本文提出的方法具有較高的可信性。

表2　任務可靠度計算結果對比分析

為驗證仿真結果的收斂性，對該系統在8 640 h時的任務可靠性進行了重復仿真。由圖4可知，仿真結果服從正態分布，任務可靠度的均值為0.142 2，其在置信水平為0.95時的置信區間為(0.138 4，0.146 0)。由此可見，本文提出的方法收斂性較好。

圖4　仿真結果的正態分布檢驗

4結束語

本文基于蒙特卡洛模擬法，對復雜系統執行使命任務的過程進行模擬，使用線性同余發生器抽樣得到其組成單元的故障時間和維修時間，依此分析該系統的任務可靠性。通過結果對比可以發現，使用蒙特卡洛模擬法得到的可靠性仿真結果誤差較小，收斂性也較好；從數據方面證實了基于蒙特卡洛法的復雜系統可靠性仿真原理，也可以進一步推廣到艦船更復雜的系統之中，對艦船可靠性進行評估和改進。

參考文獻：

[1]張玉濤,唐俊,張明清.基于蒙特卡羅方法的可靠性仿真過程模型研究[J].系統工程與電子技術,2008,30(7):1374-1377.

[2]劉欽文,趙品倫.基于蒙特卡羅的系統任務可靠性分析方法[J].可靠性與環境適應性理論研究,2013,5(31):17-22.

[3]賀驍,劉蕓江,劉梅,等.一種蒙特卡羅方法的改進方案[J].中國科技論文,2014,9(1):71-75.

[4]董艷秋,田敬博.蒙特卡洛法結構可靠性分析[J].黑龍江工程學院學報,2010,24(1):27-30.

[5]廖敏輝,柴光遠.蒙特卡洛模擬法在液壓系統可靠性設計中的應用[J].機床與液壓,2013:41(11):194-196.

[6]羅蓮.基于AHP與模糊綜合評判法在城市軌道交通線網規劃中的應用[J].重慶工商大學學報：自然科學版，2014，31(4)：46-50.

[7]喻華,魏來生.改進的故障樹monte-carlo數字仿真[J].車輛與動力技術,2006(3):35-37.

[8]Land E H ,McCann J J .Lightness and Retinex theory [J].Journal of the Optical Society of America ,1971,61(1):1-11.

[9]張國志.復雜系統可靠性研究[D].北京:北京工業大學,2009.

[10]潘豐旻，江明，周加文.基于NS2的優先級隊列管理算法設計[J].重慶工商大學學報：自然科學版，2014，31(11)：45-49.

[11]馮三營,裴麗芳.復雜系統可靠性的模擬算法研究[J].洛陽師范學院學報,2009,28(2):21-24.

[12]劉麗娜.基于遺傳算法的庫存仿真及優化[D].重慶:重慶大學,2010.

[13]周月閣,葉雪榮,翟國富.基于性能退化和Monte Carlo仿真的系統性能可靠性評估[J].儀器儀表學報,2014,5(5):1185-1191

(責任編輯唐定國)