基于地統計學變異函數理論的HMA壓實均勻性影響分析

董　喆

(河北省高速公路廊坊北三縣管理處　廊坊　065000)

基于地統計學變異函數理論的HMA壓實均勻性影響分析

董喆

(河北省高速公路廊坊北三縣管理處廊坊065000)

摘要現在常規的路面結構分析設計方法如多級層狀分析方法、AASHTO路面結構設計方法都是基于計算模型中材料的均勻性。文中應用Bomag IC Evib方法對試驗路壓實區域100%覆蓋測量其回彈模量，基于測量的非均勻分布的結果建立三維有限元模型模擬熱拌瀝青路面的彎沉響應，應用(M-E PDG) 模型預測路面結構疲勞壽命。將瀝青層模量看作空間異構分布，地統計學中的變異函數模型用于評價預測結果的均勻性。結果表明，材料模量的均勻程度對瀝青路面路用性能影響巨大。材料彈性模量的非均勻分布可以加劇彎沉的危害并縮短路面結構疲勞壽命。

關鍵詞地統計學變異函數模量彎沉疲勞壽命

現在常規的路面結構分析設計方法如多級層狀分析方法、AASHTO路面結構設計方法都是基于計算模型中材料的均勻性。即認為同種路面材料性質相同，然而，實際施工過程中，雖然對壓實攤鋪工序有著嚴格規定，但攤鋪過程中還是不可避免地會出現材料離析，局部松鋪；壓實過程中機械的停車、轉彎等導致路面結構差異化的因素。近幾年，隨著智能壓實技術在熱拌瀝青路面中的應用[1]，可以定量評價路面材料的壓實效果。為了研究路面結構壓實的均勻性，本文試驗路壓實區域100%覆蓋測量其回彈模量，并基于測量的非均勻分布的結果建立三維有限元模型模擬熱拌瀝青路面的力學響應。采用(M-EPDG) 模型預測路面結構彎沉和疲勞壽命。將地統計學中的半方差模型用于評價預測結果的均勻性。與常規路面結構分析設計方法不同，本文將瀝青層模量看作空間異構分布。結果表明材料模量的均勻程度對瀝青路面路用性能影響巨大。材料彈性模量的非均勻分布可以加劇彎沉分布不均的危害并縮短路面結構疲勞壽命。本文的案例中，非均勻模型的疲勞壽命均值與峰值相差52.67%，而均勻模型的差值只有0.1%。部分區域的路面結構材料模量下降不一定導致路面結構路用性能降低，因為路面結構材料均勻程度對路用性能起主導作用。因此，今后路面結構設計中應該考慮材料模量的非均勻分布特性。

1　研究方法

地統計學[2]是研究那些分布于空間中并顯示出一定結構性和隨機性的自然現象，其理論基礎主要是區域化變量，所謂區域化變量是指以空間點(xu，xv，xw)為自變量的隨機場Z(xu，xv，xw)[3-4]。區域化變量Z(x)具有兩重性，即隨機性和結構性。觀測前，Z(x)是一個隨機場，具有隨機的、局部的、異常的性質；觀測后，Z(x)是一個普通的空間三元函數值或空間點函數值，變量在點x和x+h(h為空間距離)處的數值Z(x)與Z(x+h)具有某種程度的自相關，這種自相關依賴于2點間的距離及變量特征，體現其結構性[5]。表面上相互矛盾的2種性質，卻能使區域化變量在所研究的某種自然現象的空間結構和空間過程方面發揮獨特的優勢。區域化變量的結構分析是以變異函數模型為基礎的，這也是變異函數的主要功能之一。

變異函數是地統計學計算的基礎，它既可以解釋區域化變量的隨機性，又可以描述區域化變量的空間結構性，是地統計學特有的基本工具。設Z(x)為區域化隨機變量，滿足本征假設和二階平穩假設，h為2樣本點空間分隔距離，Z(xi)和Z(xi+h)為區域化變量Z(x)在xi和xi+h上的觀測值(i=1,2,…,N(h))，根據協方差函數定義，其樣本的協方差函數值通過下式進行計算。

(1)

根據變異函數的定義，其樣本的變異函數值通過下式進行計算。

(2)

式中：N(h)為在(xi+h,xi)之間用來計算樣本的變異函數值的樣本對數。

對不同的空間分割距離，根據式(2)可以計算出相應的變異函數值γ (h)，以γ(h)為縱坐標、h為橫坐標進行連線，就可得到變異函數曲線圖。該曲線圖可以直接地展示區域化變量的空間變異特點，它是空間變異分析和結構分析的有效工具。

以實際調查數據作為基礎資料，應用有限元分析模擬路面結構受力狀況，有限元計算模型參數見圖1，主要分析路面結構彎沉和疲勞壽命。應用M-EPDG[6]預測的路面結構疲勞壽命計算公式

(3)

式中：εt為HMA層底的拉應變；E為瀝青層的豎向回彈應變；C為修正系數，C=10M，M=4.84(Vb+(Va-Vb)-0.69)。其中：Vb為粘結劑含量；Va為HMA的孔隙率。

本文采用的路面結構模型參數見圖1，只考慮HMA壓實不均勻分布導致的該層抗壓回彈模量不均勻性，其他結構層仍然按照均勻分布計算(見圖2)，根據瀝青路面大修時等效結構層厚度公式推導HMA層回彈模量計算公式

(4)

式中：E1為瀝青面層回彈模量；Ee為瀝青面層以下結構整體回彈模量；h1為瀝青面層厚度；he為瀝青面層以下結構總厚度。

仿真模型平面尺寸采用100m×3.75m模擬單車道在移動的行車荷載以20～80km/h車速行駛下的路面性能，為了對比說明問題，按照壓實效果分布均勻與否建立2種有限元仿真模型見圖1。圖1a)檢測的HMA層抗壓回彈模量非均勻分布情況，近似服從均值為1 486MPa的正態分布；圖1b)對比實驗中HMA層抗壓回彈模量均勻分布，均值為1 486MPa。瀝青混凝土面層模量不均勻分布及測點位置見圖2。

圖1　路面結構參數示意圖

圖2　瀝青混凝土面層模量不均勻分布及測點位置圖

由圖2檢測結果可知，由于壓實不均勻性導致同一條路面結構其抗壓回彈模量分布也是不均勻的，將其按照分布相似程度劃分成3個區域，見表1，并計算各個區域內抗壓回彈模量分布特征。

表1　不同區段壓實后回彈模量分布情況　MPa

2　計算結果分析

建立ANSYS有限元模型模擬在上述工況下路面結構性能變化趨勢，分別計算標準軸載(100kN)以不同車速(20，40，60，80km/h)駛過路面時對路面結構性能的影響。圖3，圖4分別為車速對路面彎沉的影響和路面疲勞使用壽命的影響。車速由20km/h提高到80km/h時，彎沉平均值增長了57.14%，路面結構疲勞壽命降低了52.67%；而且車速對彎沉的影響可近似擬合成線性模型，疲勞壽命曲線則非線性減小，可見車輛的沖擊作用對路面結構損壞有很大影響。

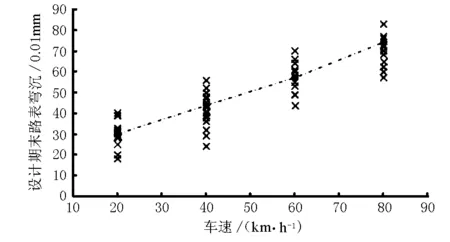
圖3　車速對彎沉影響

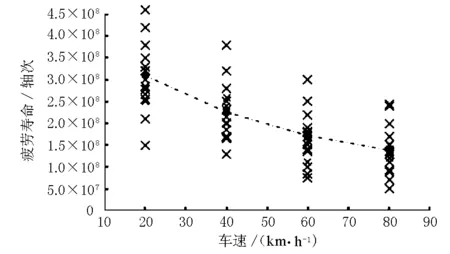
圖4　車速對路面疲勞壽命的影響

路面彎沉和疲勞壽命的縱向分布見圖5，圖6。與均勻模型計算結果對比可知，壓實度不均勻會導致路面結構的性能分布差異明顯：①路面結構非均勻壓實模型的彎沉大于均勻模型的彎沉。非均勻模型計算結果中彎沉低于均勻模型中彎沉的路段占55.1%。而非均勻模型中彎沉的平均值、95%保證率、峰值均高于均勻模型得到的結果，分別高出4.4%,37.7%,84.7%；②非均勻模型中的彎沉峰值出現在壓實分布不均勻區域，路面回彈模量分布較低區域，其彎沉普遍較大；③路面結構非均勻壓實模型的疲勞壽命低于均勻模型的疲勞壽命，非均勻模型計算結果中疲勞壽命低于均勻模型中疲勞壽命的路段占59.1%。而非均勻模型中疲勞壽命的平均值、95%保證率、峰值均次于均勻模型得到的結果，相差依次為6.2%,43.4%,94.5%；④非均勻路面結構模型中疲勞壽命極小值出現在路面回彈模量發生明顯突變區域。

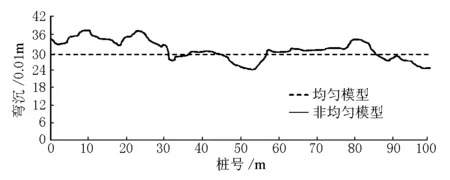
圖5　路面結構模型計算彎沉對比

圖6　路面結構模型疲勞壽命對比

3　變異函數擬合分析

為了量化研究壓實均勻性對路面結構性能的影響，采用地統計學的變異函數擬合路面不均勻壓實后的回彈模量、彎沉、疲勞壽命。根據式(2)分別計算3個區域1，2，3的變異函數值γ(h)，變異函數曲線擬合結果見圖7、圖8、圖9及表2。

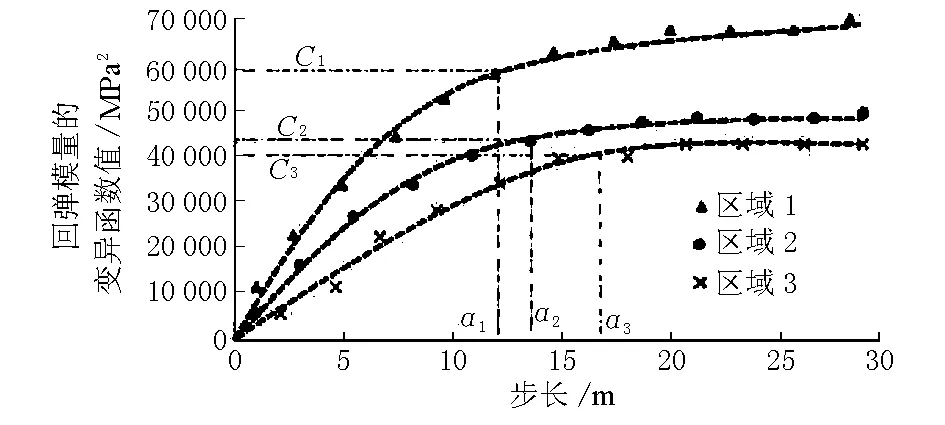
圖7　回彈模量變異分析

圖8　路表彎沉變異分析

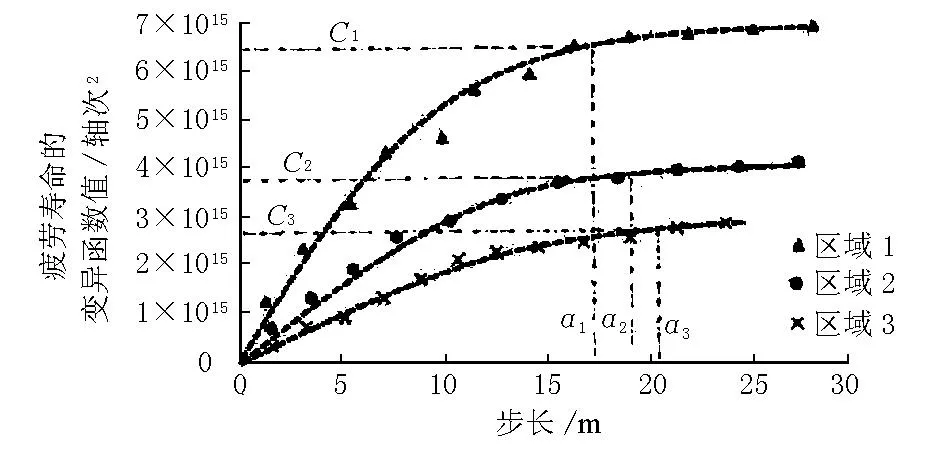
圖9　疲勞壽命變異分析

通過變異函數曲線分析路面回彈模量、彎沉、疲勞壽命的空間變異性。主要考慮變異函數曲線中2個最重要的參數：變程和基臺值。變程大小反映區域化變量影響范圍的大小，或說反映該變量自相關范圍的大小，基臺值大小則反映變量變化幅度的大小。

表2　變異函數變程和基臺值

通過變異函數曲線分析路面回彈模量、彎沉、疲勞壽命的空間變異性。主要考慮變異函數曲線中2個最重要的參數：變程(用C表示)和基臺值(用a表示)。變程C的大小反映區域化變量影響范圍的大小，或說反映該變量自相關范圍的大小，基臺值a大小則反映變量變化幅度的大小。

由圖7～圖9得出如下結論：①路面回彈模量變異函數曲線中區域1和區域2的變程低于區域3，區域1和區域2的變程分別為12.3m和13.8m，而區域3的變程為16.78m；路面疲勞壽命變程與此相似，區域1和區域2的變程分別為18.1m和19.3m，而區域3的變程只有13.9m，疲勞使用壽命變異函數中區域1和區域2的變程分別為16.5m和18.3m，區域3變程為21.0m，說明對于回彈模量和路面疲勞使用壽命而言，區域1和區域2的空間變異性小于區域3的空間變異性；②設計期末彎沉的變異函數中3個區域的變程從區域1到區域3一次減小，分別為22.1,19.6,15.1m，與路面回彈模量和疲勞使用壽命變化規律正好相反;③從縱向上看，對于區域1、區域2、區域3的共同點是彎沉變異函數的變程平均值最大，回彈模量的變程平均值最小，說明對于不均勻壓實路面結構，壓實度影響程度由小到大依次是回彈模量、疲勞使用壽命、彎沉；④區域1、區域2、區域3的基臺值變化規律與變程變化規律相反，從區域1到區域3回彈模量的基臺值依次減小，彎沉的基臺值一次增大，疲勞壽命的基臺值依次減小; ⑤回彈模量基臺值最大變化率49.03%，彎沉基臺值變化率99.75%，疲勞壽命基臺值變化率142.86%。

4　結論

(1) 非均勻壓實會導致路面結構性能下降，對于不同的評價指標，影響程度和影響區域不同。非均勻模型中的彎沉峰值出現在壓實分布不均勻區域，路面回彈模量分布較低區域，其彎沉普遍較大；非均勻路面結構模型中疲勞壽命極小值出現在路面回彈模量發生明顯突變區域。

(2) 路面回彈模量的變異性越大，路面使用性能、彎沉、疲勞使用壽命的變異性也越大，但是二者不是絕對正相關關系，比如區域1的回彈模量的變異性小于區域2，同樣區域1的彎沉變異性也小于區域2，但是對于路面疲勞使用壽命，區域1的變異性反而大于區域2。

(3) 從縱向上看，對于區域1、區域2、區域3的共同點是彎沉變異函數的變程平均值最大，回彈模量的變程平均值最小，說明對于不均勻壓實路面結構，壓實度影響程度由小到大依次是回彈模量、疲勞使用壽命、彎沉。

(4) 回彈模量基臺值最大變化率49.03%，彎沉基臺值變化率99.75%，疲勞壽命基臺值變化率142.86%，說明回彈模量大小對疲勞壽命影響程度大于對彎沉影響程度。

參考文獻

[1]楊璐,馮占強.智能壓實技術發展概況[J].工程機械文摘,2011(1):19.

[2]李秋.淺談瀝青路面質量控制[J].交通科技,2014(S1):93-95.

[3]郭懷成, 周豐,刀谞.地統計方法學研究進展[J].地理研究,2008,27(5):1191-1202.

[4]王政權.地統計學及其在生態學中的應用[M].北京：科學出版社，1999.

[5]侯景儒，郭光裕.礦床統計預測及地質統計學的理論與應用[M].北京：冶金工業出版社，1993.

[6]AppliedResearchAssociate,Inc.ideformechanistic-empiricaldesign[R].NCHRP1-137AFinalReport，2004.

收稿日期：2014-10-15

DOI10.3963/j.issn.1671-7570.2015.04.017