基于模糊神經網絡的機場噪聲煩惱度模型學習

馮 霞，張聰穎，盧 敏

（1.中國民航大學 計算機科學與技術學院，天津300300；2.中國民航信息技術科研基地，天津300300）

0 引 言

常用機場噪聲評估方法依據噪聲水平評估機場噪聲影響程度，即僅考慮聲學因素，如現在通用的美國綜合噪聲模型INM （integrated noise model）［1，2］。也有研究人員提出機場噪聲煩惱度的概念，即通過分析機場噪聲水平與機場周邊居民煩惱度之間的關系，評估機場噪聲帶來的影響［3］，該研究思路在一定程度上已經考慮到機場周邊居民的主觀感受。然僅考慮噪聲水平在實際應用中存在一定的局限性［4］。

文獻 ［5］針對現在機場噪聲評估方法在實際應用中存在的局限性，提出了一種基于模糊邏輯的機場噪聲煩惱度評估模型，該評估模型綜合考慮聲學因素與非聲學因素，以一種定量的方式評估機場周邊的噪聲影響，但該模型中的模糊規則庫依據專家知識構建，致使模型在一定程度上具有主觀性。

模糊神經網絡結合了模糊理論處理不確定的特性及神經網絡學習的能力［6－8］，利用模糊神經網絡的學習能力對機場噪聲煩惱度模型進行學習，進而對模型中的權值調整，可以使該模型的構建更具有客觀性，但在學習過程中，出現收斂速度慢、學習效率低的問題。

本文的貢獻在于提出一種針對機場噪聲煩惱度模型的混合學習方法：首先基于聚類思想，重新對模糊集合進行分組，并采用先粗學習再細學習的間接模型學習方法；然后改進傳統的基于梯度的模糊神經網絡學習算法，并將該算法應用于模型的間接學習過程中，其中改進方法為將高斯隸屬函數寬度dij的倒數σij看作獨立變量，并以σij代替dij完成模型的整個訓練過程。實驗結果表明，本文提出的混合學習方法，可以快速收斂，減少了誤差求解過程中的計算量，提高了機場噪聲煩惱度模型的學習效率。

1 用于機場噪聲煩惱度模型學習中的模糊神經網絡結構

1.1 機場噪聲煩惱度模型

機場噪聲煩惱度模型是文獻 ［5］提出的一種機場噪聲綜合評估模型，該模型綜合考慮聲學因素 （噪聲水平）及非聲學因素 （噪聲發生時間段和噪聲影響區域類型），可以更貼切地反映機場噪聲所帶來的影響，其模型構建流程如圖1所示。

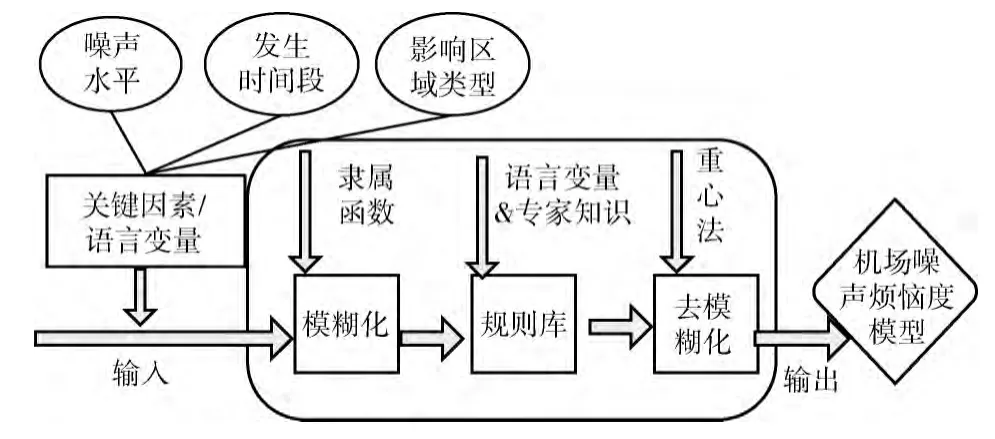
圖1 機場噪聲煩惱度模型構建流程

該模型輸入變量即為噪聲水平、噪聲發生時間段和噪聲影響區域類型，輸入變量使用高斯隸屬函數進行模糊化，基于專家知識構建模糊規則庫，采用重心法進行去模糊化操作，最終輸出機場噪聲煩惱度值。其中基于專家知識構建的模糊規則庫，具有一定的主觀性，因此本文基于模糊神經網絡對該模型進行學習，同時針對在學習過程中存在的計算量大、收斂速度慢的缺點，提出了一種改進的學習算法。

1.2 模糊神經網絡基本結構

模糊神經網絡是模糊系統與神經網絡的結合物，集中了模糊系統處理不確定性問題的長處和神經網絡學習能力的優點。本文采用的模糊神經網絡結構 （fuzzy－neural network）的網絡拓撲結構如圖2所示，它是一個具有n個輸入變量x＝ （x1，x2，…，xn）T∈Rn和一個輸出變量y∈R的四層網絡。

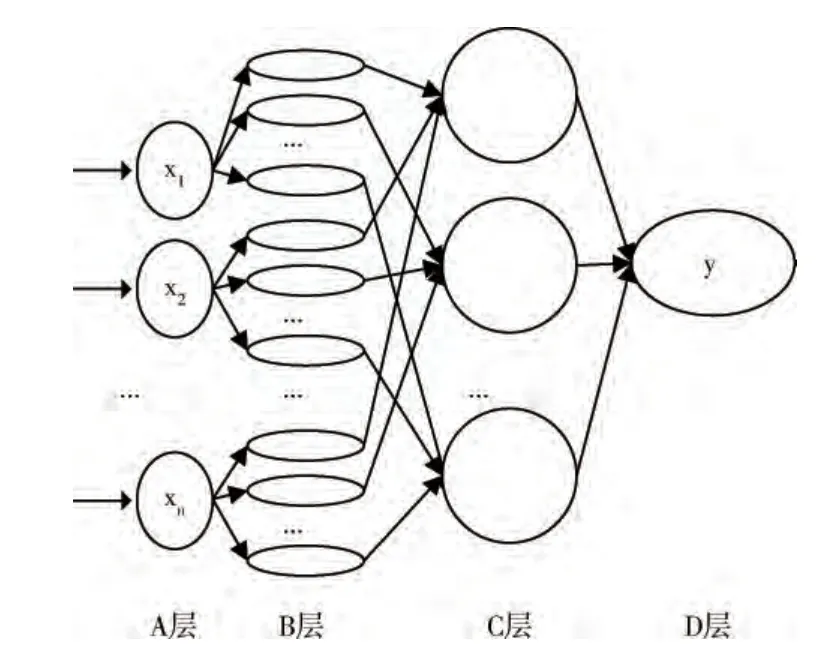
圖2 模糊神經網絡的網絡拓撲結構

圖2中，A 層 （輸入層）：該層的每個節點代表一個輸入變量，它將輸入直接傳遞到B層節點處。

B層 （隸屬函數層）：該層的每個節點代表一個輸入變量的隸屬函數。該層的作用為確定各個輸入變量的隸屬度。

C層 （模糊規則層）：該層的每個節點代表一條模糊規則，所有節點組成模糊神經網絡的規則庫，規則的形式定義為［9］：Rule s：IF x1is A1sand x2is A2sand…and xnis AnsTHEN y is ys，其中，s（s＝1，2，…，m）表示相應的第s條規則，m 為模糊規則條數，ys是輸出空間上的一個實數，Ais是xi的一個模糊子集。該層的作用是采用乘積方法，計算每條規則對應的適用度。

D 層 （輸出層）：基于重心法進行去模糊化，得到數值型輸出，其中C層到D 層的權值為wi。

1.3 機場噪聲煩惱度模型每層對應的輸出

采用模糊神經網絡對機場噪聲煩惱度模型進行學習時，每層對應的輸出為：

A層：模型中的輸入變量為噪聲水平、噪聲影響區域類型、噪聲發生時間段，即節點輸出為：＝xi，i＝1，2，3。

B層：機場噪聲煩惱度模型中，依據輸入變量的特性，采用高斯函數作為輸入變量的隸屬函數［5］，高斯函數定義為f（x，d，c）＝exp （－ （x－c）2／d2），中心值c和寬度d作為A 層到B層的權值。該層節點的輸出為：＝exp（－（－cij）2／），i＝1，2，3；j＝1，2，…，k，其中ij代表該節點是第i個輸入節點的第j個模糊值。

2 基于梯度的模糊神經學習算法的機場噪聲煩惱度模型學習

常用的模糊神經學習算法有BP （back－propagation）算法［10］，但BP算法在模糊神經網絡學習過程中，存在收斂速度慢，易陷入局部極小等缺點，盡管已有許多學者對模糊神經網絡的學習算法進行了研究［11，12］，但在機場噪聲煩惱度模型學習的適用方面仍存在計算量大，學習效率低的問題。本文采用兩種學習模式：直接學習和間接學習。直接學習指將機場噪聲煩惱度模型中所有模糊規則一起學習，間接學習指將機場噪聲煩惱度模型中的模糊規則分為兩個階段進行學習，第一個階段 （即模型中模糊規則的粗學習）依據文獻 ［13］的規則簡化方法將模型的規則簡化，然后將簡化后的規則一起學習，第二階段 （即模型中模糊規則的細學習）以第一階段學習結果作為基礎進行擴展，將擴展后的規則一起學習，這樣做避免了從頭學習所帶來的麻煩。

2.1 基于梯度的模糊神經學習算法

（1）基于梯度的模糊神經學習算法中誤差函數如下所示

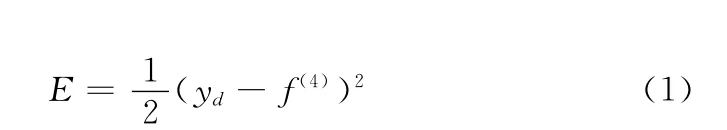
式中：yd——模糊神經網絡的期望輸出；f（4）——模糊神經網絡的實際輸出；E——期望輸出和實際輸出間的誤差。

（2）模型學習中的參數修正如下所示

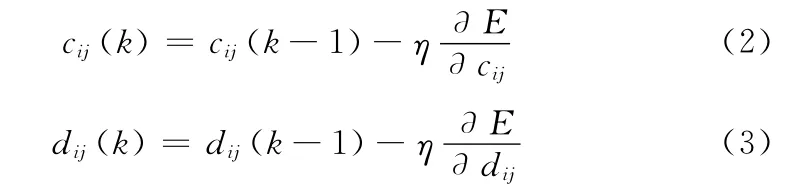
其中，cij，dij分別為高斯隸屬函數的中心和寬度，η （η＞0）為學習率，作用為決定梯度下降搜索中的步長。誤差函數E 對cij和對dij的偏導如式 （4）、式 （5）所示在算法迭代過程中，對參數不斷調整，當誤差函數達到設定值時，停止迭代，模型學習結束。

2.2 機場噪聲煩惱度模型直接學習

選取機場噪聲煩惱度模型中的60條規則作為直接學習的實驗數據［5］見表1，其中輸入變量Noise Level（VL、LL、ME、HH、VH）、Period of day （Mor.、Aft.、Nig.）、Type of zone （Business、Residential、School、Hospital）分別表示噪聲水平、噪聲發生時間段、噪聲影響區域類型。輸入變量Noise Level的模糊語言值有：VL、LL、ME、HH、VH，分別表示非常低噪聲、較低噪聲、中度噪聲、高噪聲、非常高噪聲；輸入變量Period of day的模糊語言值有：Mor.、Aft.、Nig.，分別表示上午、下午、夜間；輸入變量Type of zone的模糊語言值有：Business、Residential、School、Hospital，分別表示商業區、居民住宅區、學校、醫院。輸出變量Annoyance表示機場噪聲煩惱度，其模糊語言值有：NA、SA、MA、HA、EA，分別表示不煩惱、稍微煩惱、中度煩惱、非常煩惱、極度煩惱。

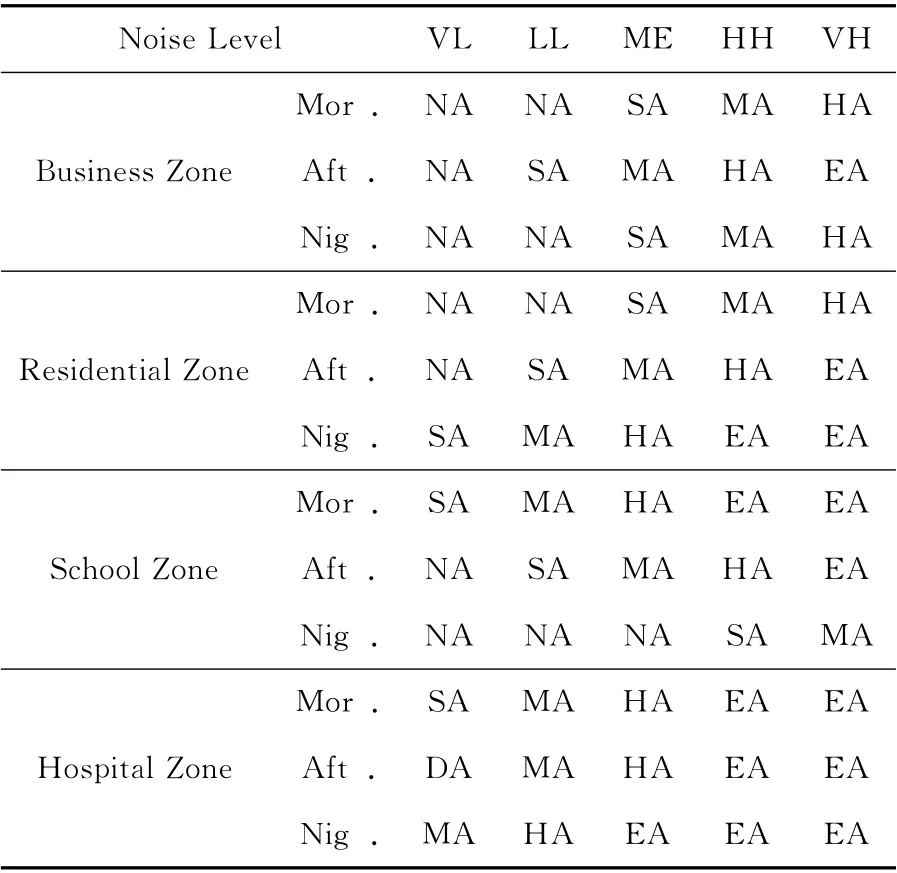
表1 機場噪聲煩惱度模型的模糊規則樣本

對該模型的學習，即通過網絡的訓練調整模型中的權值c，d，w，使得在輸入輸出誤差允許的范圍里，誤差函數E最小。

采用基于梯度的模糊神經學習算法的樣本直接學習，對60個樣本一起學習，權值的初始值隨機產生，允許誤差設置為0.07。則需經過17 360次才可達到允許誤差，如圖3所示。

2.3 機場噪聲煩惱度模型間接學習

實驗數據依然選用機場噪聲煩惱度模型中的60 條規則。采用基于梯度的模糊神經學習算法進行樣本間接學習，

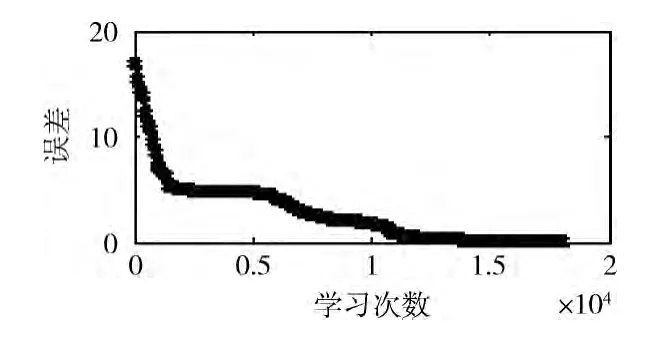
圖3 表1模糊規則直接學習結果

首先對60 個樣本進行分組學習 （即粗學習）。具體做法：依據文獻 ［13］的規則簡化方法，將表1的60個樣本簡化為表2，其中輸入變量噪聲水平 （Noise Level）粗略地分為低噪聲 （L＿N）、中度噪聲 （M＿N）、以及高噪聲 （H＿N），輸出變量噪聲煩惱度（Annoyance）精簡為低煩惱 （L＿A）、中度煩惱（M＿A）、高煩惱（H＿A），從而得到表2的36條規則，以此36條規則作樣本進行學習，權值的初始值隨機產生，經過84次就可達到0.04的誤差（如圖4所示）。

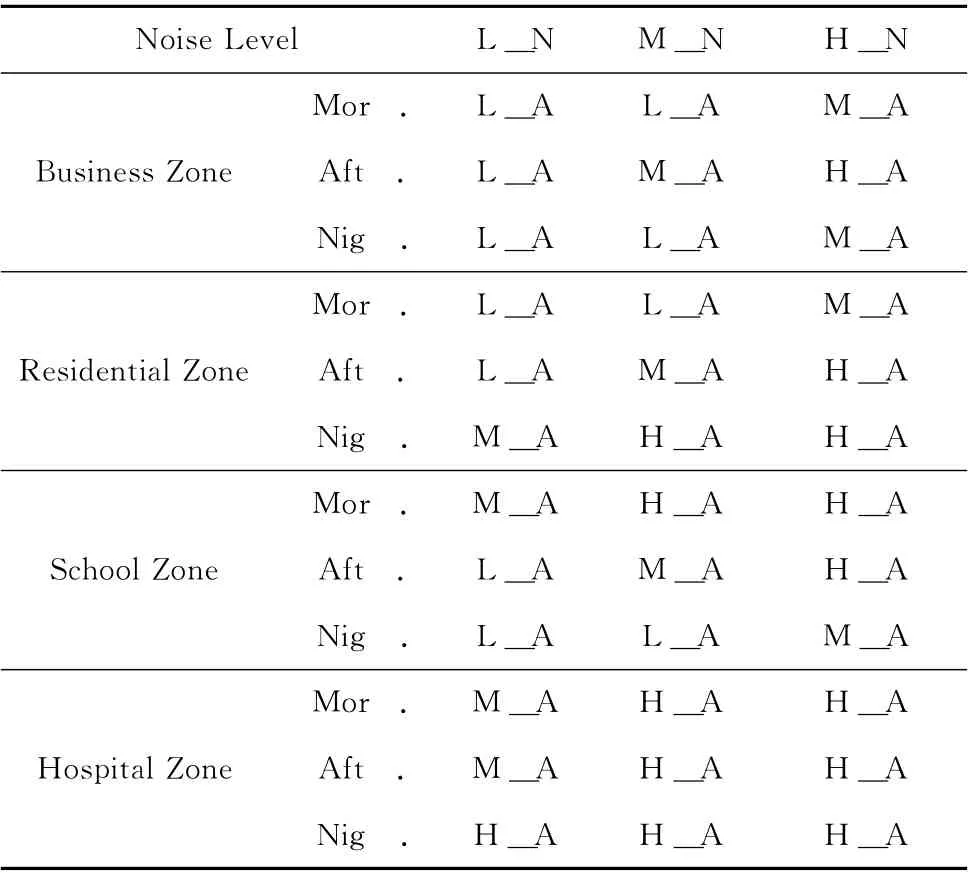
表2 簡化后模糊規則樣本

圖4 簡化后的36個樣本學習結果

經多次實驗結果表明，粗學習結果的誤差值小于0.05后，轉而進行細學習的效果較好，因此本實驗選取粗學習誤差值為0.04，之后進行細學習。

基于聚類思想，對粗略學習的結果進行擴展。具體擴展方法為：對相鄰的模糊子集給予相同的初值。例如將60個樣本學習中模糊子集VL、LL的初值都取為36個樣本學習出的L＿N 值，將HH、VH 的初值都取為H＿N，以擴展后的結果作為60 個樣本學習的初值，這樣可以避免60個樣本從頭學起的麻煩。

依然采用基于梯度的模糊神經學習算法對擴展后的規則學習，從圖5中可以看出，經過786次學習誤差就可達到小于0.07。

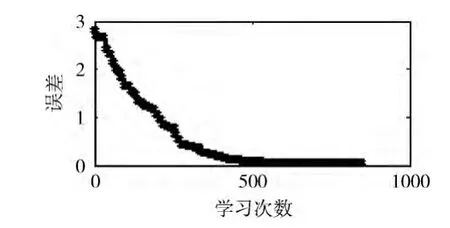
圖5 表1模糊規則的間接學習結果

3 模糊神經學習算法的機場噪聲煩惱度模型學習

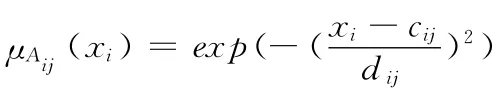
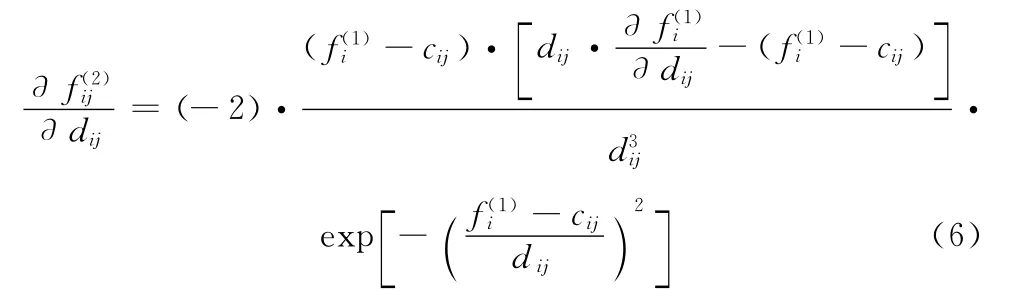
從式 （6）中可以看出，在對dij求偏導過程中，分母出現了dij三次方，當dij較小時，會在偏導求解過程中震蕩，不利于模型學習，為此，本文提出將dij的倒數σij看作獨立變量，并以σij代替dij完成整個模型訓練過程，則本文中高斯 隸 屬 函 數 可 以 表 示 為μAij（xi）＝exp（（－ （xij－cij）σij）2）。因其在訓練過程中避免了對分母的偏導求解過程，從而提高了系統的學習效率。替換后的偏導求解過程如式 （7）所示

比較式 （6）和式 （7）發現，在模型訓練過程中，式（6）中對分母求偏導的過程在式 （7）中沒有出現，這樣可以避免因dij過小，并在分母中三次方后而導致求解過程中出現的震蕩，不利于參數學習。

實驗數據依舊選取機場噪聲煩惱度模型中的60條規則樣本，在間接學習采用改進的模糊神經學習算法 （即混合學習方法），對機場噪聲煩惱度模型中的樣本先粗學習，經過78次達到0.04 的誤差，結果如圖6 所示，再細學習，經過362次便可達到0.07的誤差，結果如圖7所示。

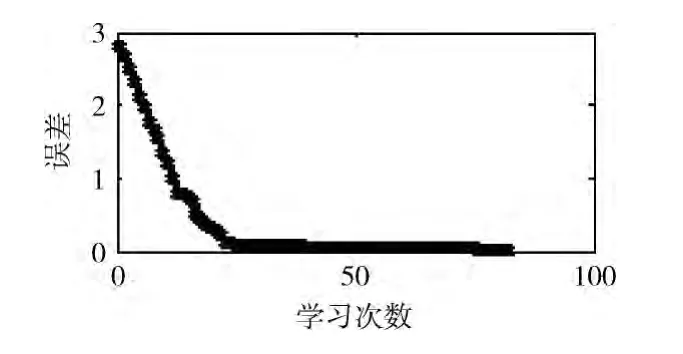
圖6 基于改進方法的36個樣本學習結果

圖7 基于改進方法的模糊規則間接學習結果

圖4與圖6均為間接學習過程中的36個樣本粗學習結果，圖5與圖7均為間接學習過程中細學習結果。采用改進的模糊神經學習算法，圖7的學習效率明顯提高，相較于圖5，圖7的學習效率提高了近乎一倍，然而在粗學習階段，效果則不是特別明顯。

4 實驗結果分析

第二節中的3組實驗結果與第三節中的2組實驗結果對比見表3，其中，在間接學習過程中采用改進的基于梯度的模糊神經學習算法，因減少了誤差求解過程中的計算量，可以快速實現收斂，相比較于間接學習中采用基于梯度的模糊神經學習算法，模型學習效率明顯提高。

表3 實驗結果對比

上述實驗結果表明，在規則量大的情況下，采用先粗學習再細學習的間接方法，相比較于樣本直接學習方法，可以有效的提高系統的學習效率，同時收斂速度更快，大大縮短了學習時間。

在間接學習過程中采用改進的模糊神經學習算法，在規則數較多情況下 （如細學過程），學習效率明顯提高，且計算量明顯減少，但在規則數較少情況下 （如粗學過程），效果不是特別顯著。改進的學習算法與傳統算法相比，減少了求誤差函數梯度過程中的計算量，從而提高了模型的學習效率。

因此本文提出的基于模糊神經網絡的機場噪聲煩惱度模型混合學習方法，在規則數較多情況下，學習效率明顯提高，收斂速度更快。

5 結束語

機場噪聲評估是實施機場噪聲控制的重要理論依據。文獻 ［5］提出了一種機場噪聲煩惱度評估模型，該模型可以更貼切地反映機場噪聲對公眾心理和精神產生的影響，同時在機場降噪航跡優化中提供重要的理論支持，但該評估模型是基于模糊邏輯構建的，具有一定的主觀性。模糊神經網絡是模糊系統與神經網絡的結合，采用模糊神經網絡可以有效地解決模型的學習問題，使模型更具有客觀性。針對機場噪聲煩惱度模型，使用傳統的基于梯度的模糊神經學習算法存在計算量大，收斂速度慢，學習效率低的問題，為此本文提出一種基于模糊神經網絡的機場噪聲煩惱度模型混合學習方法，該方法基于聚類思想，對模型采用先粗學習后細學習的間接學習策略，同時在間接學習過程中，改進基于梯度的模糊神經學習算法。

本文提出的機場噪聲煩惱度模型混合學習方法，減少了誤差函數求解過程中的計算量，加快了收斂速度，從而提高了模型的學習效率。該混合學習方法在規則數較大的情況下，可以明顯提高模型學習效率，但在規則數較少的情況下，效果不是特別明顯。

［1］XIA Ziyao，HUANG Xisheng.A study on the legislation issues of airport noise abatement in China［J］.Journal of Beijing University of Aeronautics and Astronautics （Social Sciences Edition），2011，24 （4）：38－45 （in Chinese）.［夏梓耀，黃錫生.中國機場噪聲污染防治立法問題研究 ［J］.北京航空航天大學學報：社會科學版，2011，24 （4）：38－45.］

［2］Kiani Sadr M，Nassiri P，Hosseini M，et al.Assessment of land use compatibility and noise pollution at imam khomeini international airport［J］.Journal of Air Transport Management，2014，34：49－56.

［3］JIAO Peng，CAI Liangcai.Annoyance of aircraft noise in military airfields ［J］.Environmental Science ＆ Technology，2008，31 （9）：50－52 （in Chinese）.［焦鵬，蔡良才.軍用機場飛機噪聲主觀煩惱度研究 ［J］.環境科學與技術，2008，31（9）：50－52.］

［4］Heleno T，Slama J G.Fuzzy modeling of annoyance caused by aircraft noise using LAeqD and LAeqN MetricsD and LAeqN metrics ［J］.Journal of Aerospace Technology and Management，2013，5 （1）：103－110.

［5］Feng Xia，Zhang Congying，Lu Min，et al.An airport noise annoyance model and its application on BCIA ［J］.Energy Education Science and Technology Part A：Energy Science and Research，2014，32 （4）：2375－2388.

［6］Lin Y Y，Chang J Y，Lin C T.A TSK－type－based self－evolving compensatory interval type－2 fuzzy neural network（TSCIT2FNN）and its applications［J］.IEEE Transactions on Industrial Electronics，2014，61 （1）：447－459.

［7］Yeh C Y，Jeng W R，Lee S J.Data－based system modeling using a type－2fuzzy neural network with a hybrid learning algorithm ［J］.IEEE Transactions on Neural Networks，2011，22（12）：2296－2309.

［8］Mateo J，Torres A M，García M A.Dynamic fuzzy neural network based learning algorithms for ocular artefact reduction in EEG recordings［J］.Neural Processing Letters，2014，39（1）：45－67.

［9］LI Di，CHEN Xiangjian，XU Zhijun，et al.Type－II fuzzy neural networks with self－organizing recurrent intervals for image stabilization of the airborne camera［J］.Journal of Zhejiang University（Engineering Science），2012，46 （8）：1540－1545 （in Chinese）.［李迪，陳向堅，續志軍，等.模糊神經網絡在機載相機穩像中的應用 ［J］.浙江大學學報：工學版，2012，46（8）：1540－1545.］

［10］FANG Zhenyong，YOU Wenhu，FENG Rupeng.Application of improved BP algorithm in fuzzy neural networks［J］.Journal of Beijing University of Aeronautics and Astronautics，2008，33 （11）：1321－1324 （in Chinese）. ［房振勇，游文虎，馮汝鵬.改進BP 算法在模糊神經網絡中的應用 ［J］.北京航空航天大學學報，2008，33 （11）：1321－1324.］

［11］XU Zhewan，LI Jingjiao，WANG Aixia，et al.Training algorithm of fuzzy neural network based on improved T－S fuzzy reasoning ［J］.Computer Science，2011，38 （11）：196－199（in Chinese）.［許哲萬，李晶皎，王愛俠，等.一種基于改進T－S模糊推理的模糊神經網絡學習算法 ［J］.計算機科學，2011，38 （11）：196－199.］

［12］Wu W，Li L，Yang J，et al.A modified gradient－based neuro－fuzzy learning algorithm and its convergence［J］.Information Sciences，2010，180 （9）：1630－1642.

［13］YANG Yang，WANG Guijun，YANG Yongqiang.Reducing the number of interface rules for generalized hybrid fuzzy systems based on binary tree－type hierarchy ［J］.Control Theory ＆ Applications，2013，30 （6）：765－772（in Chinese）.［楊陽，王貴君，楊永強.基于二叉樹型分層的廣義混合模糊系統推理規則數的縮減［J］.控制理論與應用，2013，30 （6）：765－772.］