基于角速率與角增量的捷聯慣導姿態算法

尹劍，鄧宏林，楊萌，張琬琳

（西安應用光學研究所，西安710065）

基于角速率與角增量的捷聯慣導姿態算法

尹劍，鄧宏林，楊萌，張琬琳

（西安應用光學研究所，西安710065）

對于捷聯慣性姿態計算來說，目前存在著多種算法。這些算法如何歸類、區分、如何在進行算法設計時根據具體應用進行算法選擇，很容易給設計者造成困擾。針對這個問題，根據姿態算法所采用的角速率和角增量的采樣方式，配合四元數算法和方向余弦算法，采用仿真手段，對常用的捷聯姿態計算進行了歸納和分析比較，給設計捷聯姿態算法提供了參考。

捷聯慣性導航；姿態計算；角速度；角增量

隨著捷聯慣性技術的發展，新型陀螺儀如激光陀螺和光纖陀螺等已經成功地得到了應用，陀螺儀的輸出形式也不僅僅限于傳統的角速率輸出［1-5］。目前常用的輸出形式有2種，一種是角速率輸出，也就是每次采樣輸出的值是當前時刻的角速率，即陀螺敏感軸感知的機體坐標系下該坐標軸相對于慣性坐標系的角速率ωib；另一種是陀螺輸出時將采樣周期Δt內的角速率進行了積分，從而輸出了采樣間隔周期內的角增量，即。根據這2種不同的采樣方式，在進行捷聯姿態計算時，相應的姿態算法也有所不同［6-8］。通常而言，對于角速率采樣，采用直接求解姿態更新微分方程的方法，工程上常用四階龍格庫塔法實現。對于該算法，根據姿態計算使用的參數的不同，又分為四參數的四元數龍格庫塔法和九參數的方向余弦龍格庫塔法；對于角增量采樣，一般采用求解姿態微分方程的解析算法，同樣，根據姿態計算使用的參數的不同，分為四參數的四元數必卡逼近法，根據采樣數目不同又細分為四元數等效旋轉矢量的單子樣、雙子樣、三、四子樣等多子樣算法以及九參數的方向余弦算法，以及方向余弦的單子樣、雙子樣及多子樣算法［9-10］。下面將對基于角速率和基于角增量的上述算法進行簡要的分析比較。

1 角速度采樣姿態算法

采用角速率采樣的捷聯姿態算法常用的有四元數法和方向余弦法。對于這2種算法，由于角速率采樣的值是姿態微分方程的計算參數，因此通常采用直接進行微分方程求解的計算方法，龍格庫塔法是工程上經常使用的方法。龍格庫塔法根據泰勒級數展開的誤差項階數不同可以分為一階、二階、三階、四階等等，工程上需要綜合考慮實現的難度及精度，四階龍格庫塔法比較常用。

1.1 方向余弦四階龍格庫塔法

方向余弦姿態更新微分方程為

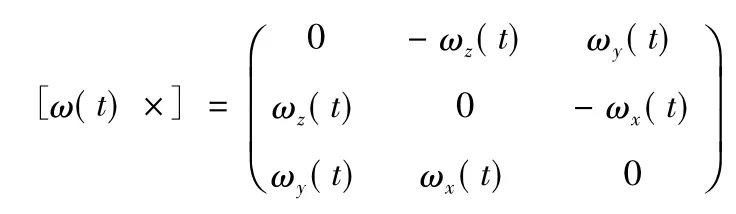
其中，ωx（t）、ωy（t）、ωz（t）分別為載體旋轉角速度t時刻時在載體坐標系X、Y和Z軸的分量，則利用四階龍格庫塔法的計算方法，在采樣周期為T的時間間隔內，按照如下分解步驟進行計算：

1.2 四元數的四階龍格庫塔法

四元數微分方程的形式為

式中：Q（t）為t時刻的姿態四元數值；

ωx（t）、ωy（t）、ωz（t）分別為飛行器旋轉角速度t時刻時在載體坐標系X、Y和Z軸的分量。利用四階龍格庫塔法的計算方法，在采樣周期為T的時間間隔內，按照如下分解步驟進行計算：

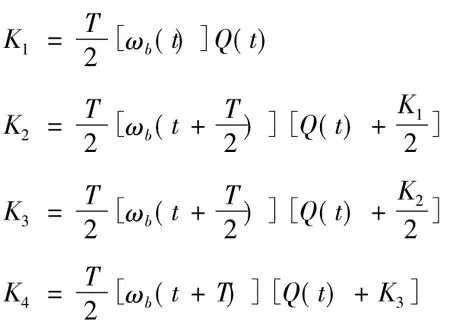
則更新后的四元數姿態值Q（t+T）為

2 角增量采樣姿態算法

對于陀螺輸出為角增量時，通常采用解姿態更新微分方程的方法，由于微分方程的解中含有角增量成方，因此在姿態更新時，可以直接采用角增量進行計算，簡化了計算流程并減少了誤差。常用的角增量姿態算法有方向余弦法和四元數法。

2.1 方向余弦角增量采樣姿態算法

采用角增量采樣時，方向余弦微分方程的解為

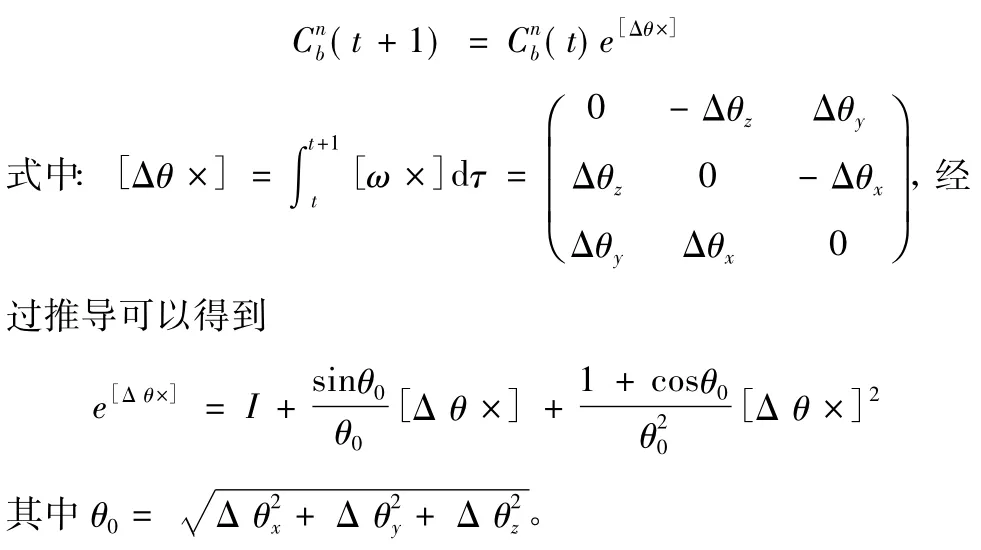
2.2 四元數角增量采樣畢卡逼近算法

四元數微分方程的解為

采用畢卡逼近法，四元數微分方程的解可以表示為

其中角增量計算式為

3 仿真分析

利用仿真的手段，對上述2種算法從精度方面進行分析，采用對捷聯慣性姿態運算來說最惡劣的工作環境條件：圓錐運動進行仿真。仿真圓錐運動的半錐角為1°，圓錐運動頻率為2 Hz，計算周期數為600點，計算頻率均為100 Hz。

仿真比較一：在上述相同的仿真條件下，比較方向余弦法與四元數法在速率采樣和角增量采樣時算法結果在精度方面的差異。圖1為采用方向余弦角速率采樣的四階龍格庫塔算法的航向角H、俯仰角φ、橫滾角θ誤差；圖2為采用四元數角速率采樣的四階龍格庫塔算法的航向角H、俯仰角φ、橫滾角θ誤差。

由上述仿真結果可見，方向余弦算法和四元數算法在使用角速率采樣的四階龍格庫塔算法時，在計算精度方面差別非常小，并且誤差變化趨勢相似。角速率算法誤差統計結果如表1所示，同樣的，在上述仿真條件下，采用每個計算周期采樣一次的單子樣角增量算法誤差統計結果如表2所示。

圖1 方向余弦四階龍格庫塔法姿態誤差

四元數四階龍格庫塔算法的航向角H、俯仰角φ、橫滾角θ誤差如圖2所示。

圖2 四元數四階龍格庫塔法姿態誤差

表1 角速率算法誤差比較

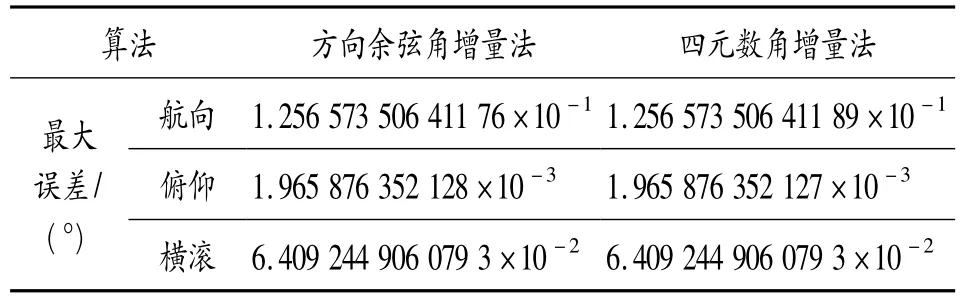
表2 角增量算法誤差比較

由表1、表2對比可以發現在相同的圓錐運動的情況下，角增量算法精度比角速率精度高幾個數量級。分析龍格庫塔算法可知，龍格庫塔法在進行計算時，在一個計算周期內利用了2次采樣數據，因此龍格庫塔算法實質上是一種雙子樣算法。下述仿真方法二將對采樣2次的角速率龍格庫塔法與角增量雙子樣算法進行比較。

仿真方法二：仍然采用上述圓錐運動方式，對角速率與角增量的算法精度進行比較。為了在采樣間隔上與角速率算法一致，角增量算法采用在一個計算周期內使用2次采樣值的雙子樣采樣算法，仿真方向余弦雙子樣算法姿態誤差如圖3所示，四元數雙子樣算法姿態誤差如圖4所示。

綜合上述仿真結果對方向余弦的角增量雙子樣算法和角速率四階龍格庫塔法以及四元數的角增量雙子樣算法與角速率的四階龍格庫塔法進行姿態誤差比較如表3所示。

圖3 方向余弦雙子樣算法姿態誤差

很容易看出無論是角增量算法還是角速率算法，方向余弦法與四元數法精度相當，雙子樣算法精度高于單子樣算法。而且，在同樣采用一個計算周期內利用2次采樣值進行姿態計算時，角增量算法精度高于角速率算法精度，這是由于陀螺輸出角增量比輸出角速率更好地保存了傳感器的實時信息，即瞬間動態特征，因而給出了更精確的測量結果，所以提高了姿態計算的精度。

圖4 四元數雙子樣算法姿態誤差

表3 算法誤差比較

4 結論

通過對比角速率采樣算法和角增量采樣姿態算法具體過程及計算姿態誤差仿真可以得到以下結論：

1）角速率采樣算法具有直觀、容易理解的特點，而角增量算法需要求解姿態微分方程，因此形式相對復雜。

2）無論采用角速率還是角增量采樣，捷聯姿態計算的2種常用算法方向余弦法與四元數法的計算精度相當，且誤差值的變化趨勢相似。

3）在相同的采樣時間間隔內，采用角增量姿態算法比采用角速率姿態算法的精度要高，這是由于角增量采樣較好地保存了陀螺傳感器的測量信息。

4）在一個計算周期內采樣2次比采樣一次算法的計算精度高，這是因為采樣次數越多，越能克服慣性姿態計算中的不可交換誤差，從而提高了姿態計算精度。

［1］秦永元.慣性導航［M］.西安:西北工業大學出版社，2006.

［2］胡小平.自主導航理論與應用［M］.長沙:國防科技大學出版社，2002.

［3］鄧正隆.慣性技術［M］.哈爾濱:哈爾濱工業大學出版社，2006:140-180.

［4］楊培根，龔智炳.光電慣性技術［M］.北京:兵器工業出版社.1999:195-199.

［5］高伯龍，李樹棠.激光陀螺［M］.長沙:國防科技大學出版社，1984.

［6］郭來軍，彭書家，白洪梅，等.彈載慣性測量單元檢測系統的設計與實現［J］.四川兵工學報，2014（4）:15-18.

［7］張琬琳，尹劍，郭栓運.Q-MEMS陀螺零偏補償技術研究［J］.應用光學，2010，7（4）:549-552.

［8］倪興，李曉勇，薛國虎，等.測量船姿態誤差影響分析［J］.四川兵工學報，2014（5）:149-151.

［9］Savage P G.Strapdown inertial navigation integration algorithm design，Part 1:attitude algorithms［J］.Journal of Guidance Control and Dynamics，1998，21（1）:19-28.

［10］Lee J G，Park C G，Park H W.Multiposition alignment of strapdown inertial navigation system［J］.IEEE Transactions on Aerospace and Electronic Systems，1993，29（4）:306 -311.

（責任編輯楊繼森）

Strapdown Inertial Navigation Attitude Algorithm Based on Angle Velocity and Angle Increment

YIN Jian，DENG Hong-lin，YANG Meng，ZHANG Wan-lin
（Xi'an Institute of Applied Optics，Xi'an 710065，China）

There are many algorithms in strapdown inertial navigation attitude calculation field.But it always puzzled the designers about how to classify them and how to select appropriate attitude algorithm.To solve this problem，some widely used attitude algorithms such as quaternion method and direction cosine matrix method were classified based on angle velocity sampling and angle increment sampling.Analysis and comparison of these algorithms were presented by simulation method.

strapdown inertial navigation；attitude algorithm；angle velocity；angle increment

尹劍，鄧宏林，楊萌，等.基于角速率與角增量的捷聯慣導姿態算法［J］.四川兵工學報，2015（11）：101 -104.

format：YIN Jian，DENG Hong-lin，YANG Meng，et al.Strapdown Inertial Navigation Attitude Algorithm Based on Angle Velocity and Angle Increment［J］.Journal of Sichuan Ordnance，2015（11）：101-104.

U666.12

A

1006-0707（2015）11-0101-05

10.11809/scbgxb2015.11.027

2015-06-09

尹劍（1972—），男，博士研究生，高級工程師，主要從事光電定位定向技術研究。