基于模糊控制的三級倒立擺系統(tǒng)仿真

李勇泉

（國電南瑞科技股份有限公司，江蘇 南京 211106）

基于模糊控制的三級倒立擺系統(tǒng)仿真

李勇泉

（國電南瑞科技股份有限公司，江蘇 南京 211106）

倒立擺是理想的自動控制試驗對象，應(yīng)用模糊控制方法，研究了三級倒立擺系統(tǒng)的穩(wěn)定控制問題。通過對系統(tǒng)的線性化模型設(shè)計LQR最優(yōu)控制反饋權(quán)陣，并基于最優(yōu)線性控制的反饋參數(shù)選擇模糊控制參數(shù)。仿真結(jié)果表明該方法可實(shí)現(xiàn)三級倒立擺系統(tǒng)的穩(wěn)定控制，具有參數(shù)選擇簡單、動態(tài)性能較好等特點(diǎn)。

三級倒立擺；模糊控制；LQR；仿真

1 引言

倒立擺系統(tǒng)是典型的非線性、強(qiáng)耦合、多變量、自然不穩(wěn)定系統(tǒng)[1]。在控制過程中，它能有效地反映諸如可鎮(zhèn)定性、魯棒性、隨動性以及跟蹤等許多控制中的關(guān)鍵問題，是檢驗各種控制理論的理想模型。迄今，人們已經(jīng)利用古典控制理論、現(xiàn)代控制理論以及各種智能控制理論實(shí)現(xiàn)了多種倒立擺系統(tǒng)的穩(wěn)定控制問題，包括LQR算法[2]、模糊控制方法[3]、模糊神經(jīng)網(wǎng)絡(luò)方法[4]等。

對于三級倒立擺這樣典型的多變量非線性系統(tǒng)，由于變量個數(shù)較多，采用模糊控制時，模糊規(guī)則的總數(shù)呈指數(shù)增長，不利用實(shí)時處理[5]。通過對多個變量進(jìn)行融合，對模糊控制器的輸入變量進(jìn)行降維，減小了模糊規(guī)則設(shè)計難度，同時也提高了系統(tǒng)控制的實(shí)時性能。

本文針對三級道理擺系統(tǒng)設(shè)計了基于融合結(jié)構(gòu)的模糊控制器，其多變量的融合權(quán)重則根據(jù)線性化模型的最優(yōu)線性控制反饋權(quán)陣進(jìn)行選取，該控制方法結(jié)構(gòu)簡單，控制穩(wěn)定，具有較好的收斂性。

2 三級倒立擺系統(tǒng)模型

2.1物理模型

如圖1所示，三級倒立擺系統(tǒng)主要是由控制對象、導(dǎo)軌、電機(jī)、皮帶輪、傳動帶以及電氣測量裝置組成。控制對象由小車、一擺、二擺、三擺組成。一擺、二擺、三擺由軸承連接，并且可以在平行導(dǎo)軌鉛垂平面內(nèi)自由轉(zhuǎn)動。

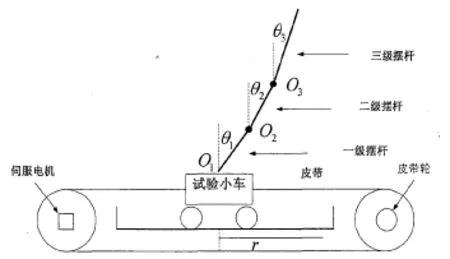
圖1　三級倒立擺物理系統(tǒng)結(jié)構(gòu)圖

2.2數(shù)學(xué)模型

對于圖 1所示的三級倒立擺系統(tǒng)，為了研究方便，假設(shè)如下條件成立：

（a）各部的摩擦力矩與相對速度（角速度）成比例；

（b）皮帶輪與傳動帶之間無滑動，傳動帶無伸長現(xiàn)象；

（c）一、二、三擺均可視為剛體；

則三級倒立擺系統(tǒng)的非線性動力學(xué)模型為：

其中，各個參數(shù)的含義可參考文獻(xiàn)[2]。

3 模糊控制器

3.1模糊控制器結(jié)構(gòu)設(shè)計

采用融合方法，為三級倒立擺系統(tǒng)設(shè)計模糊控制器，將8個輸入變量分為直接量和微分量兩組，并融合成 2個變量，其結(jié)構(gòu)如圖2所示：

圖2　三級倒立擺系統(tǒng)的模糊控制器結(jié)構(gòu)圖

3.2模糊控制器參數(shù)設(shè)置

針對上述結(jié)構(gòu)的模糊控制器，設(shè)置參數(shù)如下：

（1）確定輸入輸出論域

對于E和EC的論域，可以都選取為[-1,1]，Y的論域也選為[-1,1]。

（2）確定變量的語言值與隸屬度函數(shù)

對于E、EC和Y，均選取7個語言值，分別記為NB、NM、NS、ZE、PS、PM、PB。并采用“trimf”隸屬度函數(shù)，其中心值與邊界值采用Matlab默認(rèn)的均勻分布情況。

（3）確定模糊規(guī)則

按照線性融合的原則，設(shè)計的模糊規(guī)則如表1所示。

表1　三級倒立擺模糊控制器的模糊規(guī)則表

（4）確定增益參數(shù)（融合因子、量化因子和比例因子）

可根據(jù)系統(tǒng)的線性化模型設(shè)計對應(yīng)的最優(yōu)狀態(tài)反饋陣K=[k1,k2,k3,k4,k5,k6,k7,k8]，可以設(shè)定K00=5，相應(yīng)可求得增益參數(shù)如下：K1=k1/K00，K2=k2/K00，K3=k3/K00，K4=k4/K00，K5=k5/K00，K6=k6/K00，K7=k7/K00，K8=k8/K00，K0=-2K00。

采用最優(yōu)二次型性能指標(biāo)，取Q=diag(10,100,1000,10000, 0,0,0,0)和R=1，采用Matlab中l(wèi)qr()函數(shù)，可得到最優(yōu)線性控制反饋系數(shù)陣為K=[-3.1623,-57.2348,300.8179,-383.7509, -11.5829,-3.8366,5.3233,-51.9479]。從而可確定模糊控制器的融合因子為：K1=-0.6325，K2=-11.4470，K3=60.1636，K4=-76.7502，K5=-2.3166，K6=-0.7673，K7=1.0647，K8=-10.3896，同時也可確定量化因子為：KE=1，KEC=1；比例因子為：KU=-10。

（5）確定模糊推理方法

采用Mamdani模糊推理方法。

（6）確定解模糊方法

采用重心法（COG）解模糊。

4 仿真實(shí)驗與結(jié)果分析

基于Matlab環(huán)境，對三級倒立擺模糊控制系統(tǒng)進(jìn)行仿真，其初始化程序代碼如下所示：

設(shè)定系統(tǒng)初始狀態(tài)為X=[0.05, 0.08, 0.001, 0.008, 0, 0, 0, 0]，仿真運(yùn)行三級倒立擺模糊控制系統(tǒng)模型，結(jié)果顯示線速度和三個角速度最后都為0。位置曲線如圖3所示，可以看出，三級倒立擺系統(tǒng)在模糊控制器控制下，最終停在位移為0、擺桿1角度為0、擺桿2角度為0、擺桿3角度為0的位置，擺桿穩(wěn)定豎直，控制效果良好。

圖3　三級倒立擺模糊控制仿真結(jié)果

下面進(jìn)一步分析量化因子和比例因子對模糊控制器控制效果的影響。由于上述模糊控制器是通過線性狀態(tài)反饋控制器計算得到的，為了保持控制量對狀態(tài)量的近似線性關(guān)系，可以在下述約定條件下改變量化因子和比例因子的值：

（1）KE=KEC；

（2）KEKU=2K00=-10；

因此只要確定KE、KEC、KU其中某一項，其他兩項也就確定了。

當(dāng)KE=1時，查看模糊控制器的輸入端E和EC，可以發(fā)現(xiàn)E的峰值為-0.1和0.6，而EC的峰值為-0.02和0.18。故可以增大量化因子的取值，使輸入變量覆蓋控制器論域范圍。結(jié)果表明當(dāng) KE=1.5時控制系統(tǒng)仍然處于穩(wěn)定狀態(tài)。而當(dāng)KE=4時，控制系統(tǒng)的輸出呈現(xiàn)發(fā)散狀態(tài)，系統(tǒng)不穩(wěn)定，如圖4所示。因此，當(dāng)KE的范圍為1～1.5時可獲得穩(wěn)定快速的控制效果。

圖4　模糊控制仿真位置曲線（KE=4）

5 結(jié)論

本文應(yīng)用模糊控制方法，研究了三級倒立擺系統(tǒng)的穩(wěn)定控制問題。通過對系統(tǒng)的線性化模型設(shè)計 LQR最優(yōu)控制反饋權(quán)陣，并基于最優(yōu)線性控制的反饋參數(shù)設(shè)計模糊控制參數(shù)，仿真結(jié)果表明該方法可實(shí)現(xiàn)三級倒立擺系統(tǒng)的穩(wěn)定控制，這種模糊控制器的設(shè)計方法也可以應(yīng)用到其他多變量、非線性系統(tǒng)的控制問題中。

[1] 孟巧榮,廉自生.倒立擺控制系統(tǒng)的建模與仿真[J].機(jī)械工程與自動化,2004,(2):7-9.

[2] 李宇成,朱興,鄭興凱,等.基于 LQR算法的三級倒立擺控制系統(tǒng)的仿真研究[J].北方工業(yè)大學(xué)學(xué)報,2006, 18(3):35-40.

[3] 樓順天,胡昌華.基于MATLAB的系統(tǒng)分析與設(shè)計——模糊系統(tǒng)[M].西安:西安電子科技大學(xué)出版社,2001.

[4] 崔桂梅,宏曉英,秦力舒,等.狀態(tài)變量合成的三級倒立擺模糊神經(jīng)網(wǎng)絡(luò)控制[J].控制工程,2004,11(1):36-38.

[5] 曲建嶺,吳文海,孫俊恩.三級倒立擺系統(tǒng)模糊控制器設(shè)計及仿真[J].系統(tǒng)仿真學(xué)報,2004,16(3):578-588.

Triple inverted pendulum system simulation based on fuzzy control

Inverted pendulum is an ideal experimental object in automatic control area. The paper uses fuzzy control method to study the stability controlling problem of triple inverted pendulum system. The LQR optimal control feedback weight matrix is designed through the system’s linearizing model, and the feedback parameters for optimal linear control are used to decide the fuzzy controller parameters. Simulation results show that the proposed method can achieve the stability control of triple inverted pendulum, and it has a simple parameter selection with a good dynamic performance.

Triple inverted pendulum; fuzzy control; LQR; simulation

TP273

A

1008-1151(2015)06-0007-03

2015-05-11

李勇泉（1987－），男，江蘇無錫人，國電南瑞科技股份有限公司助理工程師，從事電氣自動化工作。