一端外伸梁置換法撓度轉角方程關系的完備性

喻曉今

（華東交通大學土木建筑學院，江西 南昌330013）

以簡單的撓曲線來替代較為復雜者，文獻［1］通過分析簡支梁、懸臂梁和外伸梁在集中力、集中力偶、分布載荷作用下的最大撓度，發現了簡支梁和外伸梁絕對值最大撓度與對應的懸臂梁（置換梁）自由端撓度的同一性，找到了以簡代繁的可能性。文獻［2］給出了簡支梁的比擬梁法（置換法）的轉角位移方程和撓度位移方程，適用于簡支梁，并以實例應用。文獻［3］推導出簡支梁和懸臂梁的置換法的轉角位移方程和撓度位移方程。文獻［4］則以置換法解超靜定連續梁，以置換法位移方程直接列寫變形協調關系，各型實例說明其良好的適應性。完成導出置換法解一端外伸梁的轉角位移方程和撓度位移方程的是文獻［5］的工作，這樣，置換法求解梁撓度和轉角的問題向另一類簡單支承梁擴展。在文獻［6］中，置換法用于解靜定剛架位移。對于鉸支承Γ 形剛架的位移，文獻［7］作了討論。Γ 形剛架支承的進一步增加，在文獻［8］里提出了解法。文獻［9］對一個方向無外力的剛架進行了置換法討論。而在置換法與它法結合運用上，文獻［10］有探討。為深化置換法的研究，其位移方程本身性質似待揭示。

從梁的撓曲線在其面內的幾何圖形的觀察出發，在任一位置上對撓曲線加入切線作輔助線，并且，一般地作切線的垂線——將該垂線引向梁的有關邊界點，此邊界點包括支承點和端點等等，構成直線、曲線組成的圖形，權且稱為置換法圖像。對置換法圖像進行分析，以平面幾何關系和撓曲線所表達的撓度以及其轉角為基本變量，建立起它們的等量關系，是置換法尋求位移方程的方法。前研究所找到的位移方程有撓度方程和轉角方程，為了進一步落實它們的關系，需要對其性質進行深入研究，以下證明一端外伸梁的撓度方程與轉角方程的導數關系。

1 右端外伸梁置換法位移方程之間關系

根據梁的位移的討論，梁的對稱彎曲中，在小變形條件下，梁的撓度與轉角是一階導數的關系，即有w′(x)=θ(x)，其中:w(x)是撓度；θ(x)是轉角；x是梁的橫截面在變形前的軸向位置坐標。當已經求出撓度方程（撓曲線方程）后，只要對撓度方程求關于自變量x一階導數，所得函數便是轉角方程。置換法所獲得的位移方程，包括撓度方程和轉角方程皆是關于自變量x的、并存在中間變量的復合函數，就是以置換梁自由端撓度、梁長、跨長、外伸端撓度和x等參數為變量的復合函數，此情況提示應以復合函數的求導法則來驗證其包含的撓度方程和轉角方程的一階導數關系。右端外伸梁見圖1.

1.1 右端外伸梁置換法圖像

作任一右端外伸梁置換法圖像見圖2，點劃線ABC代表梁的變形前軸線位置，其與x 軸重合，點劃線ABD為梁軸線變形以后的位置——為明晰而夸大，仍然是淺坦的彈性曲線。x軸原點在梁的左端A處。現于梁的任一位置、離點A為x處的G點處，向下方引一與y軸平行的線段GH，交撓曲線為H點，其即是梁在x位置的撓度（小變形假設）。作H點的切線JK，連接J、A兩點，并使線段AJ正交于線JK；同樣，連接K、D兩點，并使線段DK正交于線JK。顯然，線段AJ，DK分別是梁在G處的左、右置換梁自由端的撓度wl(x)，wr(x)（小變形假設）。同理，離梁的A點為x+Δx處的N點處，向下方引一與y軸平行的線段NQ，交撓曲線為Q點，其即是梁在x+Δx位置的撓度。作Q點的切線RS，連接R、A兩點，并使線段AR正交于線RS；同樣，連接S、D兩點，并使線段DS正交于線RS。顯然，線段AR，DS分別是梁在N 處的左、右置換梁自由端的撓度wl(x+Δx)，wr(x+Δx)。

另外，切線JK、RS的交點為T；線段AR與切線JK的交點為U；線段DK與切線RS的交點為V。

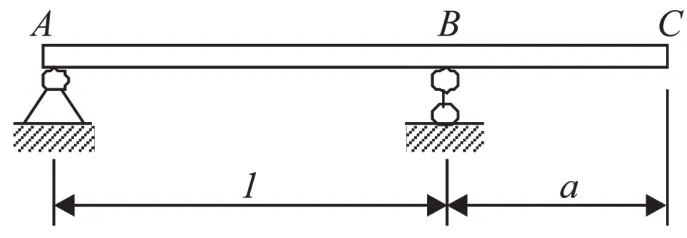
圖1 右端外伸梁Fig.1 Right end overhanging beam

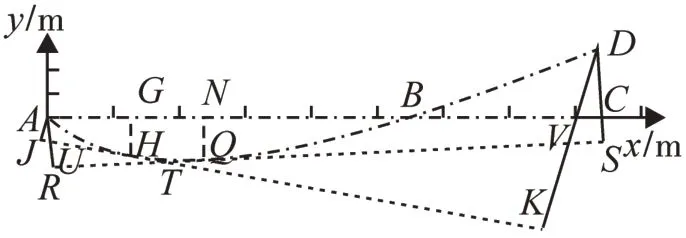
圖2 右端外伸梁置換法圖像Fig.2 Conversion method graph of right end overhanging beam

1.2 右端外伸梁撓度方程、轉角方程

在結構一定、荷載一定的條件下，參考文獻［5］給出的右端外伸梁轉角方程、撓度方程分別如下

式中：wl(x)表示左置換梁自由端撓度；wr(x)表示右置換梁自由端撓度；l表示跨度；a表示梁外伸部分長度；wC表示外伸端撓度。

式（1）代入式（2）有：

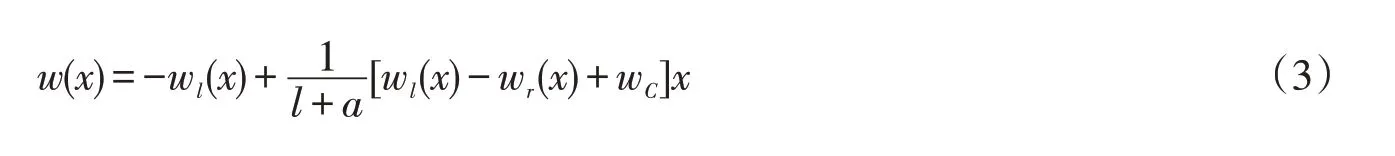
1.3 撓度方程的一階導數

對式（3）求關于自變量x一階導數，得

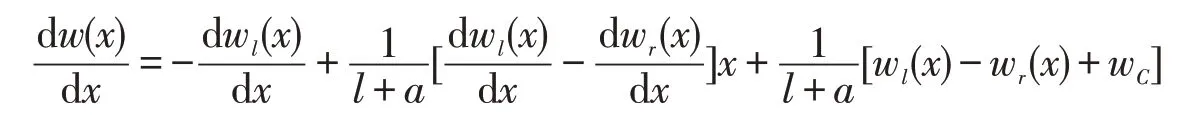
1.4 左右置換梁撓度關系的幾何特征

對式（4）中的Ω進行分析。借助于置換法圖像，研究的內涵。

研讀圖2，看直角三角形TUR，TKV，由于∠RTU=∠VTK（對頂角），故它們相似（三角形中兩角分別相等）。根據相似三角形的性質，得到等式：

由此可得

因為小變形假設，所有轉角都是微小量，并且考慮撓曲線的連續光滑性質，當Δx趨近于零時，也即N點無限地靠近G點時，Q點無限靠近H點，并與T點逐漸合為一點。與此同時，U點趨近于J點；V點趨近于S點。AJ≈AU，DV≈DS（等價無窮小），就是

將式（6）、（7）代入式（5），得：TK(AR-AJ)≈RT(DK-DS)。

再顧及這些線段的物理意義，上式即是

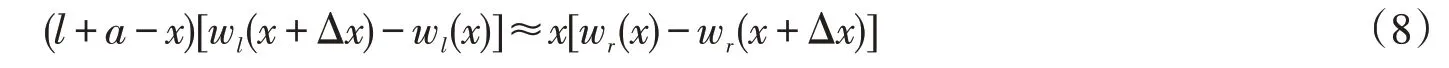
1.5 撓度轉角方程的關系

式（8）約等號兩邊同除以(l+a)Δx因子，得：

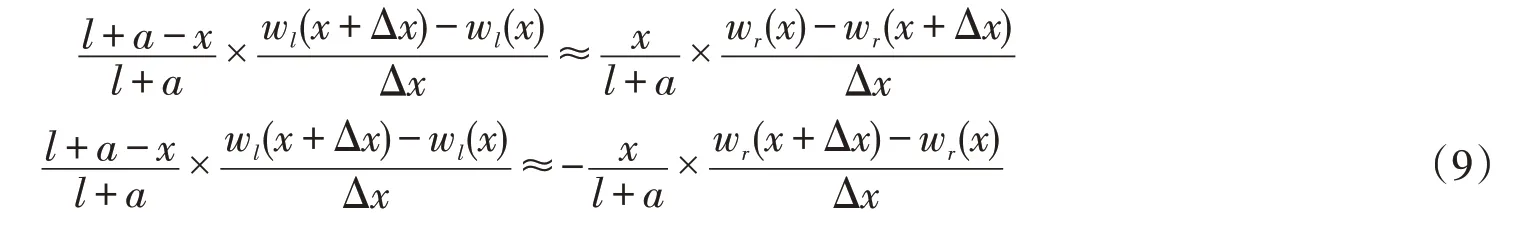
顯然，式（9）中約等號兩邊的各自第二個因子是各自函數增量與自變量的比值，依照導數定義，當Δx趨于零時下式成立：

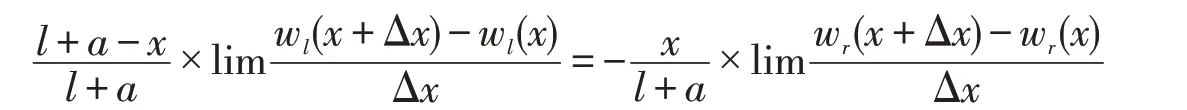
就是：

移項得：

2 左端外伸梁置換法位移方程之間關系

左端外伸梁見圖3.以下討論步驟完全與右端外伸梁的相同，為節省篇幅，采用縮略型語匯，詳細邏輯關系參看上述內容。

2.1 左端外伸梁置換法圖像

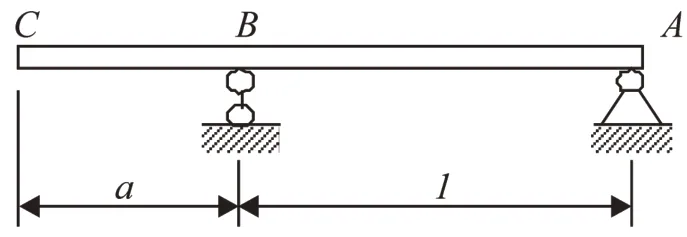
圖3 左端外伸梁Fig.3 Left end overhanging beam

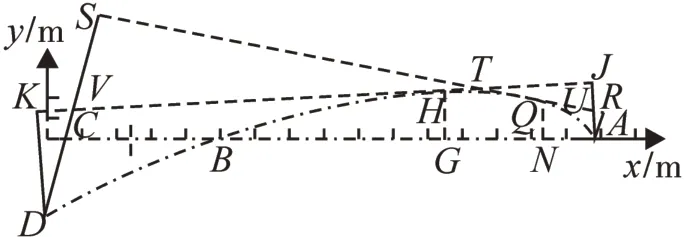
圖4 左端外伸梁置換法圖像Fig.4 Conversion method graph of right end overhanging beam

作左端外伸梁置換法圖像，見圖4.不失一般性，點劃線ABC代表梁的變形前軸線位置，其與x軸重合，點劃線ABD為梁軸線變形以后的位置，仍然是淺坦的彈性曲線。x軸原點在梁的左端C處。現于梁的任一位置、離點C為x處的G點處，向上方引一與y軸平行的線段GH，交撓曲線為H點，其即是梁在x位置的撓度。作H點的切線JK，連接J、A兩點，并使線段AJ正交于線JK；同樣，連接K、D兩點，并使線段DK正交于線JK。顯然，線段DK、AJ分別是梁在G處的左、右置換梁自由端的撓度wl(x)，wr(x)。同理，離梁的C點為x+Δx處的N點處，向上方引一與y軸平行的線段NQ，交撓曲線為Q點，其即是梁在x+Δx位置的撓度。作Q點的切線RS，連接R，A兩點，并使線段AR正交于線RS；同樣，連接S，D兩點，并使線段DS正交于線RS。顯然，線段DS、AR分別是梁在N處的左、右置換梁自由端的撓度wl(x+Δx)、wr(x+Δx)。

另外，切線JK，RS的交點為T；線段AJ與切線RS的交點為U；線段DS與切線JK的交點為V。

2.2 左端外伸梁撓度方程、轉角方程

［5］給出的左端外伸梁轉角方程、撓度方程分別如下：

式中符號意義同前。

2.3 撓度方程的一階導數

將式（10）代入式（11），再對式中變量求關于x一階導數，得：

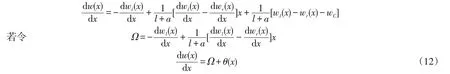
2.4 左右置換梁撓度關系的幾何特征

對式（12）中的Ω進行分析。研讀圖4，看直角三角形TUJ，TSV，由于∠JTU=∠VTS，故它們相似。得到等式：

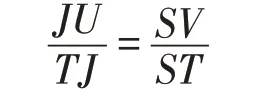
由此可得：

當Δx趨近于零時，也即N點無限地靠近G點時，Q點無限靠近H點，并與T點逐漸合為一點。與此同時，U點趨近于R點；V點趨近于K點。AR≈AU，DV≈DK，就是

將式（14），（15）代入式（13），得：

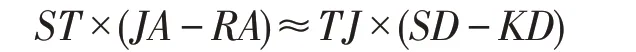
上式即是：

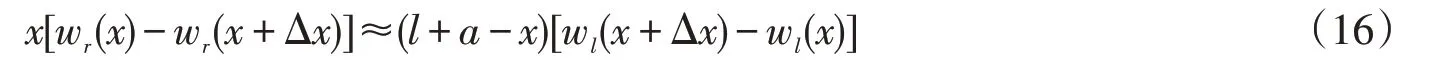
2.5 撓度轉角方程的關系

式（16）約等號兩邊同除以(l+a)Δx因子，得：

顯然，式（17）當Δx趨于零時使下式成立

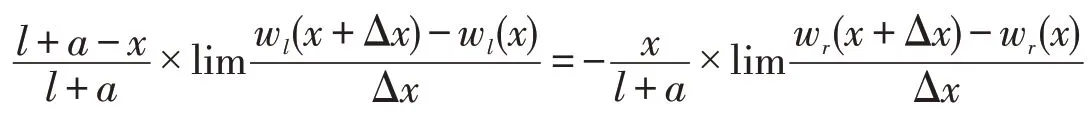
3 結論

置換法位移方程由自變量x、中間變量wl(x)和中間變量wr(x)等等構成，是一組關于x的復合函數。所述復合函數完全適應導數運算的條件和要求。

1）定義的置換梁撓度導數的協和為零。

2）一端外伸梁的置換法撓度方程、轉角方程完全符合一階導數的關系，即w′=θ，故它們也完全保有原梁撓曲線方程和轉角方程的關系性質。一端外伸梁的置換法位移方程準確可靠，可以應用于理論分析和工程實踐。

參考文獻：

[1] 喻曉今.幾種荷載下的梁絕對值最大撓度的同一性[J].華東交通大學學報,2000,17(2):40-45.

[2] 喻曉今.以比擬梁法求梁的位移[J].華東交通大學學報,2002,19(4):35-36,40.

[3] 喻曉今.求梁位移的比擬梁法[J].東華理工學院學報,2004,27(4):398-400.

[4] 喻曉今.求超靜定等直梁的置換法[J].工程力學,2007,24(S1):66-69.

[5] 喻曉今.一端外伸梁對稱彎曲彈性位移的置換法確定[J].力學與實踐,2014,36(4):478-482.

[6] 喻曉今.以置換法求靜定剛架的位移[J].江西理工大學學報,2007,12.28(6):50-52.

[7] 喻曉今.以置換法求鉸支Γ型剛架的位移[J].江西理工大學學報,2008,8.29(4):36-38.

[8] 喻曉今.超靜定Г型剛架的置換原理解答[J].華東交通大學學報,2008,12.25(6):1-5.

[9] XIAOJIN YU.Solution of slope of simple frame without force in one direction by principle of conversion method[J].Advanced Materials Research,2012:3141-3144.

[10] XIAOJIN YU.Solution of slope of a frame based on simple support beam coming from method of changing to rigidity by step combined with conversion method[J].Advanced Materials Research,2013:1889-1892.