基于非圓顆粒Trapdoor試驗模擬土拱效應

趙志國，王炳龍，韓高孝，唐 斌，梁 杰

（1.同濟大學道路與交通工程教育部重點實驗室，上海201804；2.中水電成都建設投資有限公司，成都610212；3.中國水利水電第七工程局有限公司，成都610081）

土拱現象在巖土工程實踐中較為常見［1-2］，例如樁基工程中針對土拱效應的研究，對解決樁基合理間距［3-6］、樁基承載力以及應力傳遞特性［7-9］等問題具有重要意義。另外，如何合理確定砂土地層中隧道土拱的范圍及土拱效應的穩定性是決定隧道土壓力荷載是否合理的關鍵因素［10］。實踐表明在巖土工程中充分利用拱效應，不僅有助于預防工程事故的發生，而且可以得到良好的工程效益。太沙基［11］利用砂土的Trap-door 試驗證實了土拱效應的存在，在試驗的基礎上推導了松動土壓力的解析表達式；武軍［10］基于橢球理論、陳若曦［12］考慮土拱作用下主應力偏轉、李文博［13］基于側壓力系數分別對太沙基松動土壓力公式進行了修正；Adachi［14］等利用三維砂土Trap-door試驗模擬隧道施工過程支護壓力的變化；Fin［15］運用連續介質理論給出了Trap-door 平移或旋轉時豎向應力的平面應變彈性解；Evans C H［16］給出了無黏性、均勻、各向同性土體中Trap-door 向上和向下運動時的平面應變塑性解；Koutsabelouis［17］利用有限元分析不同高寬比條件下Trap-door下降過程中Trap-door上豎向應力的變化。

雖然諸多學者針對土拱效應問題提出了不同的計算模型，但實際上土顆粒并不是連續的，應用有限元、有限差分等方法不能有效地模擬土顆粒的大變形、流動等諸多問題。離散元方法克服了傳統連續介質力學模型的宏觀連續性假設，可從細觀層面上對土的工程特性進行數值模擬，并通過細觀參數的研究來分析宏觀力學行為。

韓高孝［18］利用PFC2D中二維圓盤單元模擬砂土中的土拱效應，而文獻［19］指出黏性土顆粒可采用一系列的二維圓盤單元來模擬，直接采用二維圓盤單元來模擬砂土顆粒是不適當的。基于以上原因，本文從散粒體和細觀角度，應用非圓顆粒對砂土Trap-door試驗過程中的土拱效應進行分析，以期更真實地反應砂土中土拱效應的形成機理。

2 非圓顆粒Trapdoor試驗DEM模擬方法

2.1 非圓顆粒模擬

PFC2D中提供了模擬非圓顆粒的CLUMP方法用于非圓顆粒的二次開發，所謂CLUMP就是通過純圓顆粒的粘結組成任意形狀顆粒，顆粒之間可以重疊也可以不重疊，CLUMP單元在受力過程中不會被破壞，從而提高了非圓顆粒的計算效率。

本文即利用“團顆粒”方法，開發形狀近似橢圓的“橢圓團”顆粒模擬砂土。模擬橢圓顆粒時，首先生成純圓顆粒，然后，按照質量等效和面積等效原則進行轉化［20］，具體思路如圖1所示。

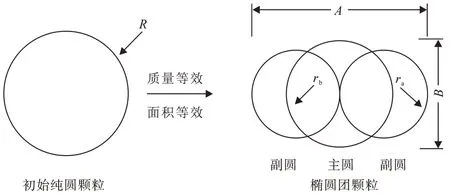
圖1 初始純圓顆粒與“橢圓團”顆粒轉化示意圖Fig.1 The conversion chart of the initial round particles to the elliptical particle

2.1.1 面積等效原則

假設純圓顆粒半徑為R，“橢圓團”顆粒由主圓顆粒和兩個副圓顆粒組成，主圓顆粒半徑為rb，副圓顆粒半徑為ra，“橢圓團”顆粒長軸長為A，短軸長為B，顆粒長短軸比為Se，則滿足

初始純圓顆粒與開發的“橢圓團”顆粒面積相等，則滿足

式中：S純圓為初始純圓顆粒面積；S主圓為“橢圓團”顆粒主圓顆粒面積；S副圓為“橢圓團”顆粒副圓顆粒面積；S疊合為“橢圓團”顆粒主圓顆粒與副圓顆粒疊合面積。

2.1.2 質量等效原則

“橢圓團”顆粒的質量是組成團顆粒的各個圓盤顆粒的質量之和，則滿足

式中：ρ純圓為初始純圓顆粒密度；ρ′為“橢圓團”顆粒密度。

2.2 Trapdoor試驗DEM模擬

2.2.1 數值試樣制備

整個數值模型中選用三面墻體模擬模型箱，模型箱大小為0.4 m×0.4 m，其中底板中心處可以移動的墻體用以模擬Trap-door，墻體剛度的取值十分關鍵，過大邊界效應明顯，過小則造成顆粒逃逸，本文取顆粒剛度的10倍，顆粒細觀參數取值參照文獻［18］的結果。

顆粒利用落雨法制備，即：①在0.4 m×0.4 m 的模型箱中生成純圓顆粒，初始孔隙比取0.45；②編寫FISH程序找到每個純圓顆粒的中心位置及其顆粒尺寸，刪除純圓顆粒，利用FISH二次開發程序按照質量等效原則和體積等效原則生成“橢圓團”顆粒；③每隔一定運算步消除顆粒中的位移場，在重力作用下顆粒下沉，刪除指定高度以上的顆粒；④反復循環，直至顆粒之間平均不平衡力與平均接觸力之比小于1%即認為顆粒制備完成，顆粒達到平衡狀態；等待試驗，最終生成Trap-door模型如圖2和圖3所示。

2.2.2 Trapdoor試驗DEM模擬方法

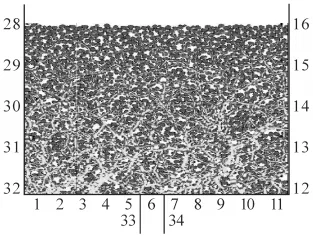
圖2 Trap-door DEM模型Fig.2 The model of the Trap-door DEM

圖3 Trap-door DEM局部放大圖Fig.3 An enlarged view of the Trap-door DEM

為了模擬非圓顆粒土拱效應，按照控制單一變量的原則，本文選擇了以下11種方案進行模擬，其中方案1、2、3和4保證顆粒形狀、顆粒摩擦系數和Trap-door寬度不變的前提下，控制Trap-door位移，用于研究Trap-door位移對土拱效應的影響；方案5和6保證顆粒摩擦系數、Trap-door寬度和Trap-door位移不變的前提下，控制顆粒形狀變化，研究顆粒長短軸比即顆粒形狀對土拱效應的影響；方案7、8和9 保證顆粒形狀、Trap-door寬度和Trap-door位移不變的前提下，改變顆粒摩擦系數，用于研究顆粒摩擦特性對土拱效應的影響；方案10和11保證顆粒形狀、顆粒摩擦系數和Trap-door位移不變的前提下，改變Trap-door寬度用于模擬Trap-door大小對土拱效應的影響，主要計算參數和方案如表1所示。

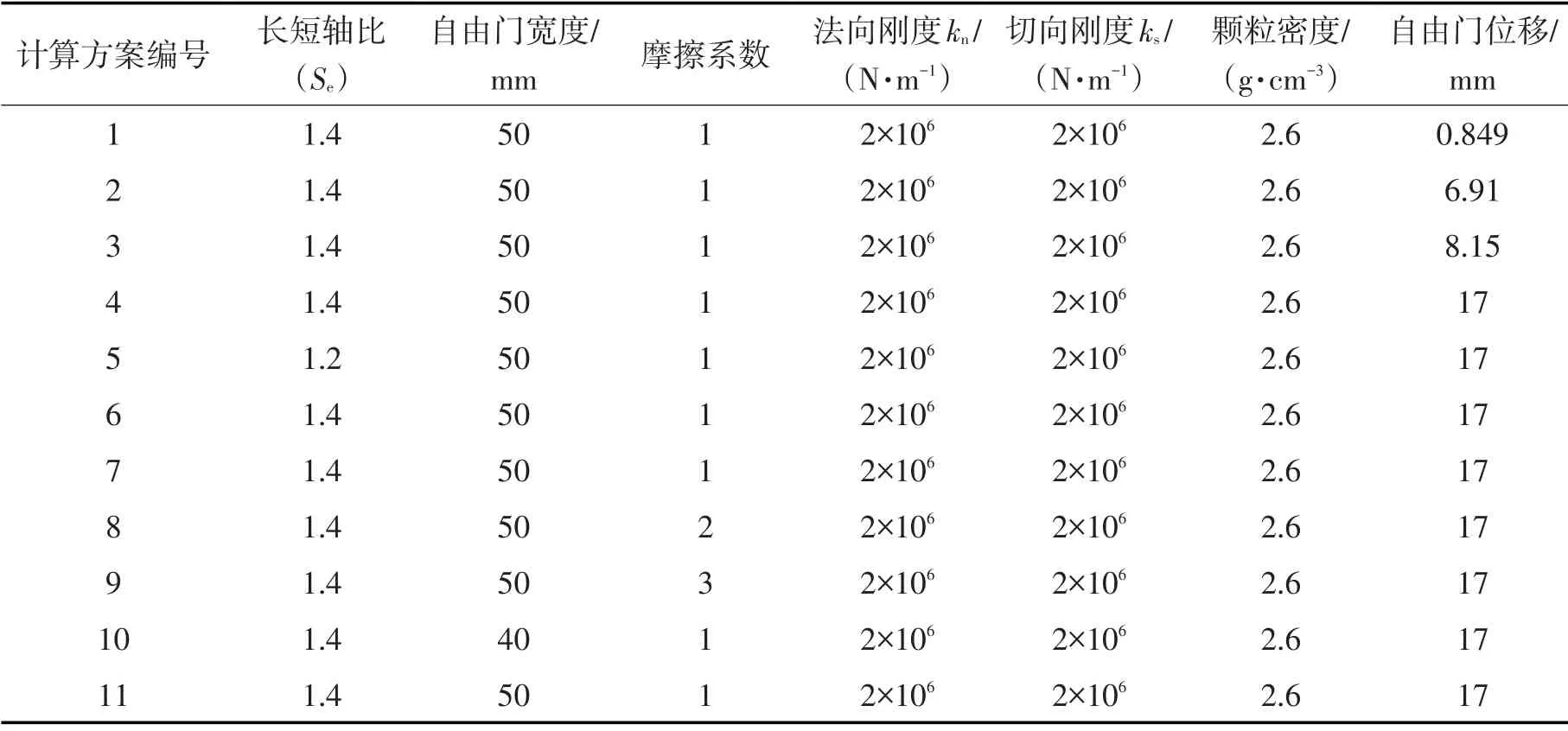
表1 計算參數及其方案表Tab.1 Calculation parameters and program

整個試驗過程中通過移動模型箱底板上的6 號墻模擬Trap-door，墻體移動速度為0.005 m·s-1，試驗過程可以認為是準靜態的，即土體內部顆粒有足夠的時間進行應力和位移調整。

3 結果分析

為了從宏觀上描述Trap-door試驗過程中的土拱效應，通過編寫相應的FISH 程序記錄模型中橫向和縱向每隔4 cm共48個監測點不同時刻的水平位移和豎向位移，同時在模型箱底板上布置直徑為8 cm的5個測量圓監測試驗過程中底板應力變化，監測點布置情況如圖4所示。

圖4 Trap-door試驗監測點布置示意圖（單位：cm）Fig.4 Arrangement of monitoring points

3.1 Trap-door位移對土拱效應的影響分析

以顆粒長短軸比為1.4、顆粒摩擦系數為1和Trap-door寬度為50 mm為例分析在不同Trap-door位移條件下“橢圓團”顆粒土拱效應。

從圖5可知，由于Trap-door 的下移，造成應力釋放，模型中不同埋深處的顆粒相應地產生沉降；隨著Trap-door的下移，距離Trap-door越遠的截面沉降越小，沉降曲線呈兩頭小、中間大的特點；在模型箱底面距離模型箱中心8 cm外沉降很小，主要影響區域寬度為16 cm，這一寬度約為3.2倍的Trap-door寬度。由圖6可知，當Trap-door位移為8.15 mm時F截面處的位移幾乎相等，即出現了所謂的等沉現象，這也是土拱效應的宏觀表現。

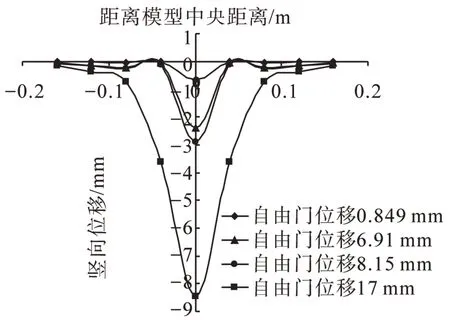
圖5 不同Trap-door位移條件下A截面位移曲線圖Fig.5 Displacement curve of A cross-section in different displacement of Trap-door

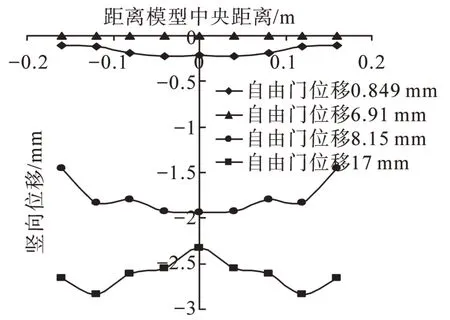
圖6 不同Trap-door位移條件下F截面位移曲線圖Fig.6 Displacement curve of F cross-section in different displacement of Trap-door

由圖7可知，當Trap-door 位移達17 mm 時，模型中顆粒最大位移為8.472 mm，小于Trap-door 位移；更為有趣的是，截面D以上的所有顆粒沉降幾乎相等，形成所謂的等沉面，這便為“橢圓團”顆粒中土拱效應的宏觀表現，而這一截面高度即為土拱效應影響的上限，上限高度約為16 cm，這一高度約為3.2倍的Trapdoor寬度。

通過布設在模型箱底板的測量圓獲得Trap-door 在移動過程中底板應力變化值，由圖8可知，隨著Trap-door 的下移，Trap-door 位移從0.849 mm 增大到17 mm 的過程中Trap-door 上的應力由202.4 N 變為952.07 N；并且，隨著Trap-door的下移，距離模型中央約5 cm范圍內底板應力大幅度減小，距離模型中央兩側各4～15 cm，模型箱底板應力有所增加，這一寬度約為2.2倍Trap-door 寬度；由此說明模型箱底板應力在不斷調整，這個過程正是土拱效應形成的過程。這一現象與文獻［21］運用砂土通過室內試驗獲得規律是一致的，這也從側面驗證了本文數值試驗模型的正確性。

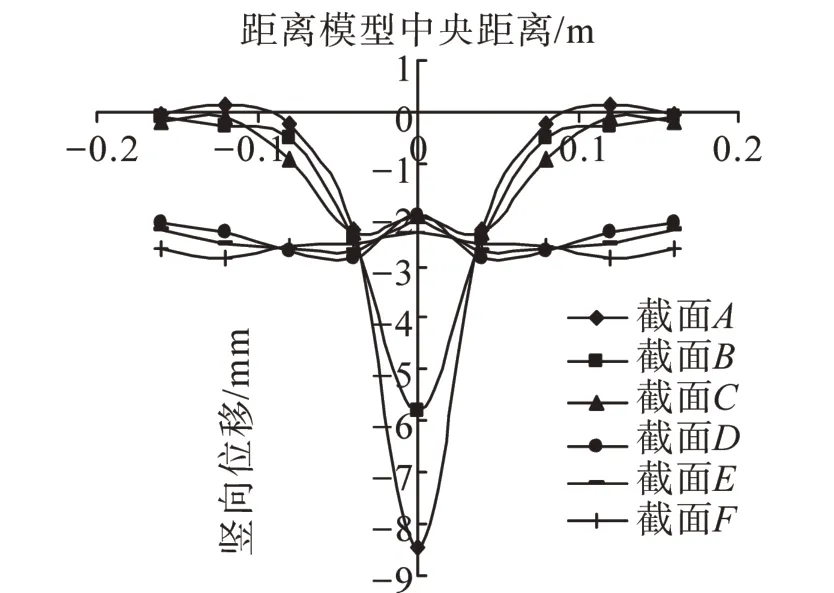
圖7 Trap-door位移為17 mm條件下各截面位移變化曲線圖Fig.7 Displacement curve of different cross-section under the condition of Trap-door displacement equal to 17 mm

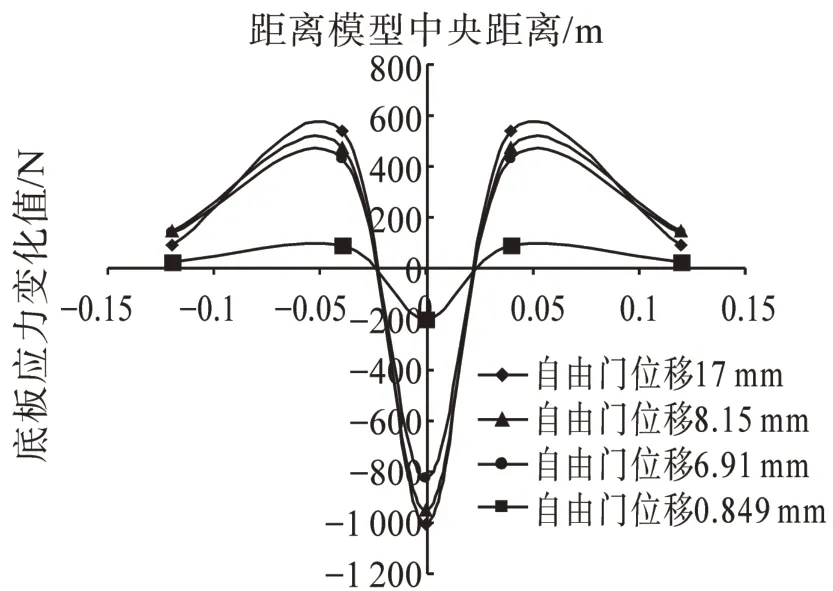
圖8 不同Trap-door位移條件下底板應力變化曲線圖Fig.8 Stress curve of floor in different displacement of Trap-door

3.2 顆粒長短軸比對土拱效應的影響分析

取Trap-door位移為17 mm時A截面顆粒豎向位移變化分析，由圖9可知，隨著顆粒長短軸比的增大，A截面顆粒豎向位移由10.66 mm減小到8.472 mm，由圖10可知，底板中心應力變化值隨著顆粒長短軸比的增大而增大，由718.8 N增大到1 008.4 N，土拱效應隨著顆粒長短軸比的增大而更加明顯。

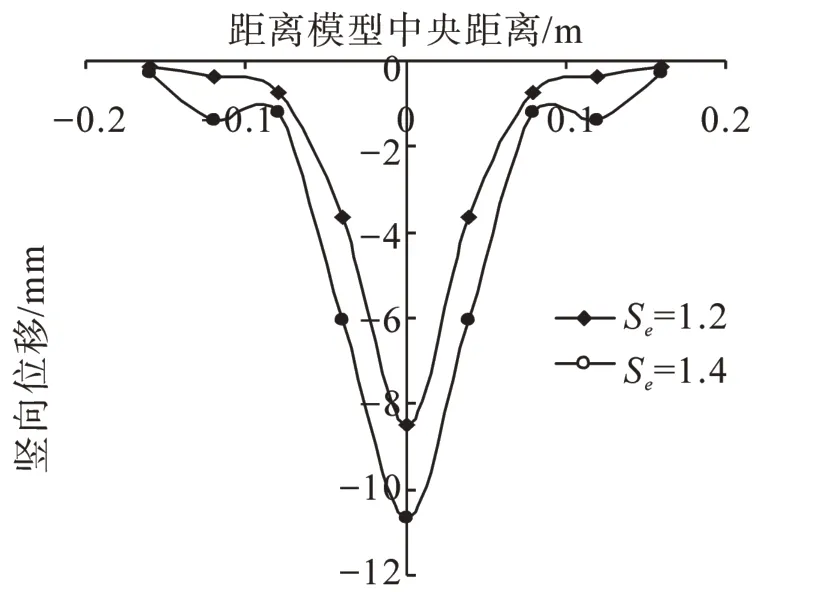
圖9 不同長短軸比A截面顆粒位移變化曲線圖Fig.9 Displacement curve of A cross-section in different ratio of axis of particle

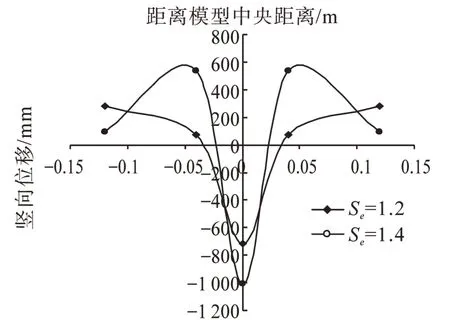
圖10 不同長短軸比底板應力變化曲線圖Fig.10 Stress curve of floor in different ratio of axis of particle

3.3 顆粒摩擦系數對土拱效應的影響分析

取Trap-door位移為17 mm時，A截面顆粒豎向位移變化分析，由圖11可知，隨著顆粒摩擦系數的增大，A截面顆粒豎向位移由12.36 mm減小到3.03 mm，由圖12可知，底板中心應力變化值隨著顆粒摩擦系數的增大而增大，由1 008.41增大至1 258.95 N，綜合可知，土拱效應隨著“橢圓團”顆粒間摩擦系數的增大而更加明顯。

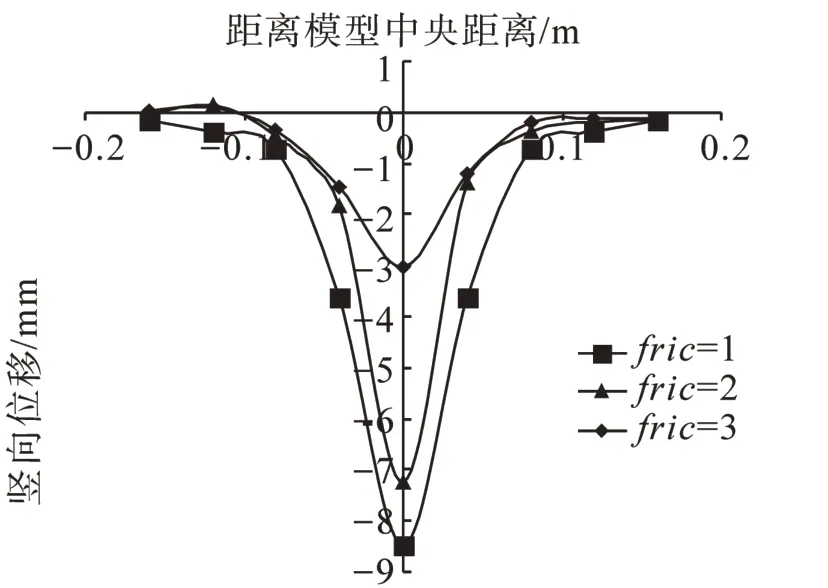
圖11 不同摩擦系數A截面顆粒位移變化曲線圖Fig.11 Displacement curve of A cross-section in different frictional coefficient

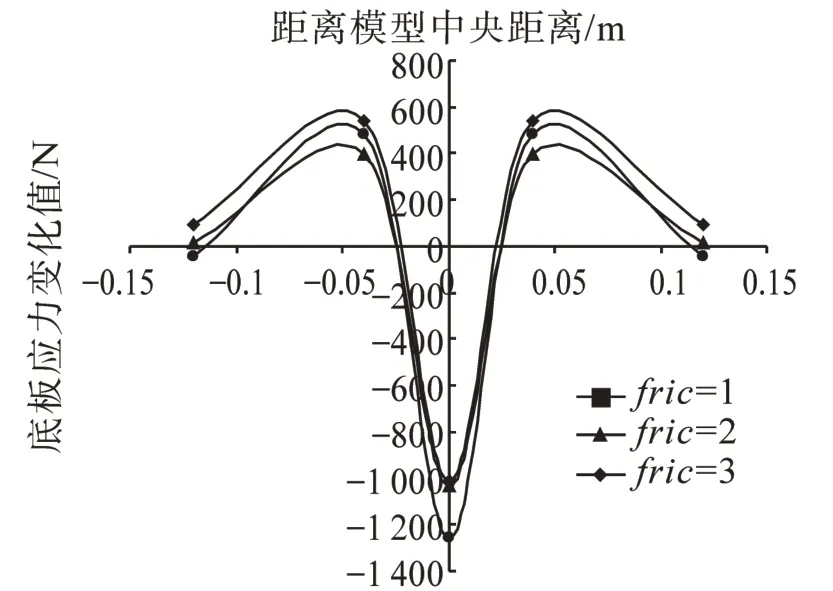
圖12 不同摩擦系數底板應力變化曲線圖Fig.12 Stress curve of floor in different frictional coefficient

3.4 Trap-door寬度對土拱效應的影響

取Trap-door 位移為17 mm 時，A截面顆粒豎向位移變化分析，由圖13 可知，隨著Trap-door 寬度的增大，A截面顆粒豎向位移由5.07 mm增大到8.47 mm；由圖14可知，底板中心應力變化值隨著Trap-door寬度的增大而減小，由1 163 N減小至1 008.4 N，綜合可知，土拱效應隨著Trap-door寬度的增大而減弱，這主要是由于應力釋放的增大所造成的。

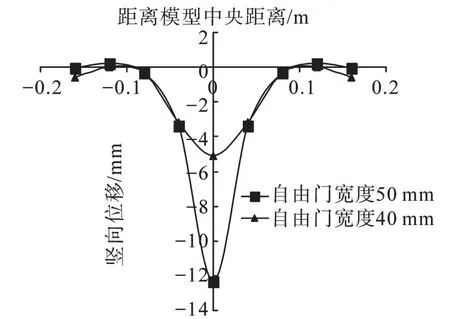
圖13 不同Trap-door寬度A截面顆粒位移變化曲線圖Fig.13 Displacement curve of A cross-section in different width of Trapdoor

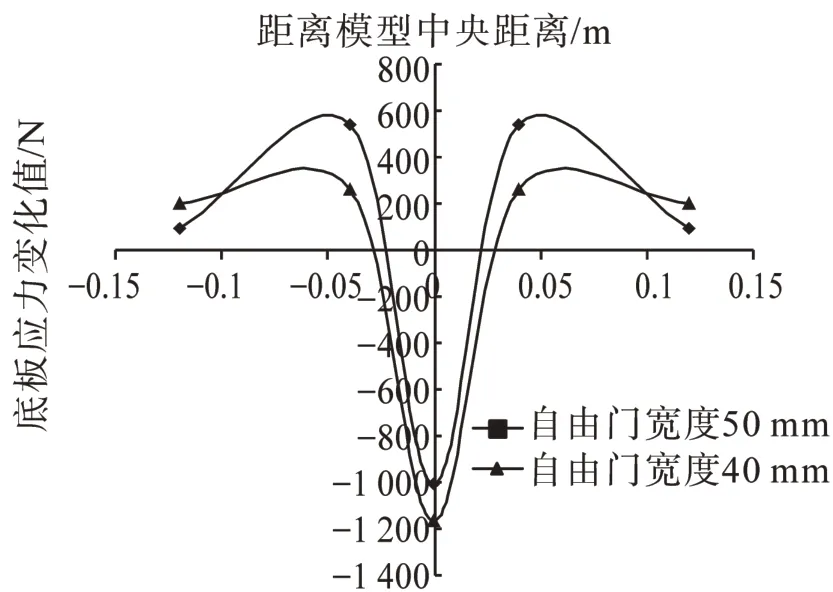
圖14 不同Trap-door寬度底板應力變化曲線圖Fig.14 Stress curve of floor in different width of Trapdoor

4 結論

本文通過應用PFC2D中CLUMP方法二次開發的“橢圓團”顆粒模擬砂土在Trapdoor試驗過程中的土拱效應，并分析了Trapdoor位移、顆粒形狀、顆粒摩擦系數和Trapdoor寬度對土拱效應的影響，最后得到如下結論：

1）顆粒長短軸比為1.4、顆粒摩擦系數為1、Trap-door寬度為50 mm時，“橢圓團”顆粒中土拱影響寬度約為3.2倍的Trap-door寬度，高度約為3.2倍的Trap-door寬度；

2）由于土拱效應，Trap-door位移從0.849 mm增大到17 mm的過程中，模型箱底板應力在不斷調整；

3）增大顆粒長短軸比、顆粒摩擦系數可以增強土拱效應；

4）減小Trap-door寬度即減小應力釋放可以增強土拱效應。

[1] 賈海莉,王成華,李江洪.關于土拱效應的幾個問題[J].西南交通大學學報,2003,38(4):398-402.

[2] 楊雪強,何世秀,莊心善.土木工程中的土拱效應[J].湖北工學院學報,1994,9(1):1-7.

[3] 楊明,姚令侃,王廣軍.樁間土拱效應離心模型試驗及數值模擬研究[J].巖土力學,2008,29(3):817-822.

[4] 蔣良濰,黃潤秋,蔣忠信.黏性土樁間土拱效應計算與樁間距分析[J].巖土力學,2006,27(3):446-450

[5] 趙明華,廖彬彬,劉思思.基于拱效應的邊坡抗滑樁樁間距計算[J].巖土力學,2010,31(4):1211-1216.

[6] 馮君,呂和林,王成華.普氏理論在確定抗滑樁間距中的應用[J].中國鐵道科學,2003,24(6):79-81.

[7] BRITTON E J,NAUGHTON P J.The arching phenomena observed in experimental trap door model tests[J].Geo-Frontiers, 2011:788-797

[8] 王漾,周萌,宮全美,等.高速鐵路CFG樁網復合結構設計參數分析[J].華東交通大學學報,2010,26(6):17-22.

[9] 元翔,宮全美,王炳龍.高速鐵路CFG樁復合地基處理方案數值模擬[J].華東交通大學學報,2008,25(1):32-36.

[10] 武軍,廖少明.基于顆粒流橢球體理論的隧道極限松動區與松動土壓力[J].巖土工程學報,2013,35(4):714-721.

[11] TERZAGHI K.Theoretical soil mechanics[M].New York:Wiley,1943.

[12] 陳若曦,朱斌,陳云敏,等.基于主應力軸旋轉理論的修正Terzaghi松動土壓力[J].巖土力學,2010,31(5):1402-1406.

[13] 李文博,陶連金,蔡東明,等.地鐵隧道豎向土壓力計算公式探討與改進[J].鐵道建筑,2013(3):78-81.

[14] ADACHI T, KIMURA M, KISHIDA K.Experiment study on the distribution of earth pressure and surface settlement through three-dimensional Trapdoor tests[J].Tunnling and underground space technology,2003,18:171-183.

[15] FINN.Boundary value problems of mechanics[J].Journal of the Soil Mechanics and Foundation Division,ASCE, 1963,89(SM5):39-72.

[16] EVANS C H.An examination of arching in granular soils[D].Cambridge:Massachusetts Institute of Technology, 1983.

[17] Koutsabelouis N C,Griffiths D V.Numerical modelling of Trap door problem[J].Geotechnique,1989,39(1):77-89.

[18] 韓高孝,宮全美,周順華.摩擦型巖土材料土拱效應微觀機制顆粒流模擬分析[J].巖土力學,2013,34(6):1791-1798.

[19] 胡欣雨,張子新.不同地層條件泥水盾構開挖面失穩狀態顆粒流模擬方法研究[J].巖土力學,2013,32(11):2258-2267.

[20] 史旦達.單調與循環加荷條件下砂土力學性質細觀模擬[D].上海:同濟大學,2007.

[21] 加瑞.盾構隧道垂直土壓力松動效應研究[D].南京:河海大學,2007.