某型彈用渦扇發(fā)動機振動故障建模與分析

王海飛，陳 果，廖仲坤，張 璋

（1.南京航空航天大學民航學院，南京210016；2.北京動力機械研究所，北京100074）

0 引言

彈用渦扇發(fā)動機由于裝配控制精度不夠，易發(fā)生轉子不平衡、支承松動、轉子不對稱、臨界轉速共振以及轉靜碰摩等故障，從而導致整機振動超標，極大地影響彈用渦扇發(fā)動機的可靠性和安全性。

為了弄清轉子系統(tǒng)各種故障機理，國內(nèi)外學者對整機建模以及故障仿真[1-8]做了大量研究工作。航空發(fā)動機故障仿真與實際排故存在較大差異，理論分析缺乏與實際振動數(shù)據(jù)的對比和驗證，因此分析結果難于應用于實際情況。國內(nèi)針對試車數(shù)據(jù)也做出大量分析[9-15]，但是缺乏理論分析。

本文針對某型彈用航空發(fā)動機試車數(shù)據(jù)在28000～30000r/min之間出現(xiàn)振動超標的情況進行排故分析。r/min

1 試車數(shù)據(jù)分析

某試車增、減速過程如圖1所示。其中，轉速V1=24000 r/min，V2=26200 r/min，V3=30000 r/min，V4為試車減速過程。從圖中可見，由V2增至V3過程中，機匣加速度振動幅值陡增。

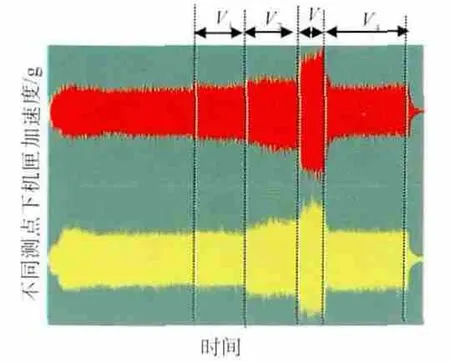
圖1 某試車增、減速過程

某試車數(shù)據(jù)水平測點1～4倍頻隨轉速的變化曲線如圖2所示。測點為壓氣機支承對應的機匣水平方向的測點。從圖中可見，在轉速升高的過程中，1倍頻增加。從水平方向的振動值來看，在轉速28000r/min下，1倍頻振幅為7g；在轉速30000r/min下，1倍頻振幅為18g，相比1倍頻，其他高倍頻分量很小。因此，初步判斷振動超標是由于在30000r/min附近出現(xiàn)了臨界轉速和過大的不平衡量所致。然而，由不平衡激勵機理可得，不平衡量激發(fā)的響應與轉速平方成正比。因此，如果在轉速28000r/min下，1倍頻振幅為7g；在轉速30000r/min下，1倍頻振幅應為7（300002/260002）=9.5g<18g。由此可見，該發(fā)動機在30000r/min附近出現(xiàn)了臨界轉速，為找到其原因需進行整機振動仿真分析。

2 航空發(fā)動機整機動力學模型

2.1 某型彈用航空發(fā)動機模型

某型彈用航空發(fā)動機的轉子-支承-機匣模型如圖3所示。其中，P1、P2、P3、P4、P5分別為風扇盤、電機盤、壓氣機盤、渦輪盤1、渦輪盤2；C1、C2分別為中介機匣、燃燒室機匣；G1、G2、G3分別為風扇軸與傳動軸套齒聯(lián)軸器、傳動軸與壓氣機軸套齒聯(lián)軸器、壓氣機軸與渦輪軸套齒聯(lián)軸器；S1、S2、S3、S4分別為風扇支點、壓氣機前支點、壓氣機后支點、渦輪支點；I1、I2分別為前、后安裝節(jié)；kg為齒輪泵嚙合剛度；kf1、kf2、kf3、kf4為轉子-機匣支承剛度；kc為機匣-基礎連接剛度。

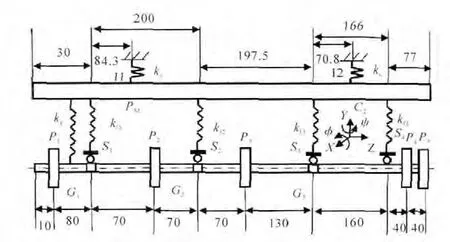
圖3 某型彈用航空發(fā)動機的轉子-支承-機匣模型

2.2 動力學建模

2.2.1 轉子系統(tǒng)的動力學模型

有限元轉子動力學模型如圖4所示。其中轉子節(jié)點上的力和力矩分別為整機中部件之間的耦合力和力矩，設轉子的自由度為

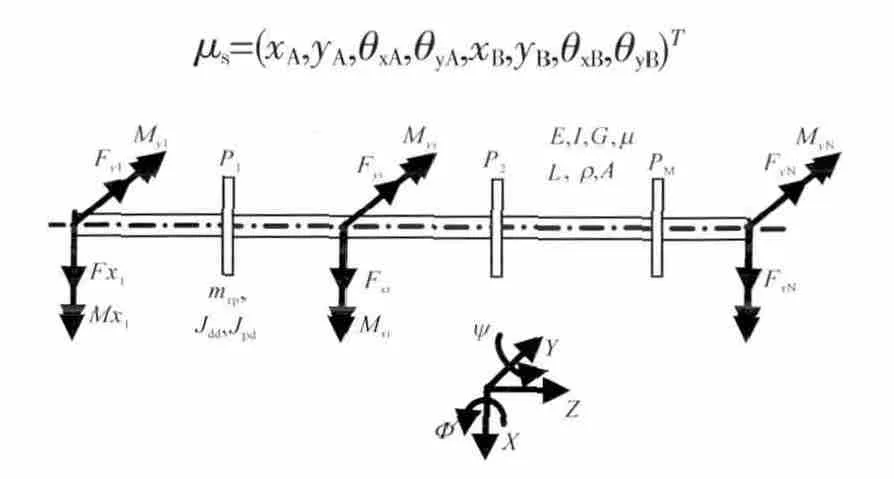
圖4 有限元轉子動力學模型

則轉子系統(tǒng)的運動方程為

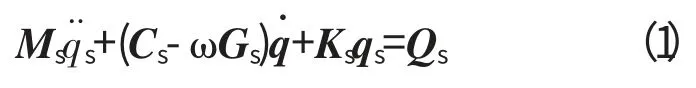
式中：Ms、Cs、Gs、Ks、Qs分別為系統(tǒng)的質量矩陣、阻尼矩陣、陀螺力矩矩陣、剛度矩陣和所承受的載荷。

采用比例阻尼，即Cs=α0Μs+α1Ks，得到第i 階阻尼比為

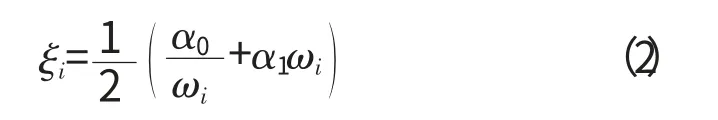
通過轉子任意2階固有頻率和阻尼比，求解α0,α1和Cs。

2.2.2 機匣模型

本文假設機匣為不旋轉的梁，得到其運動方程為

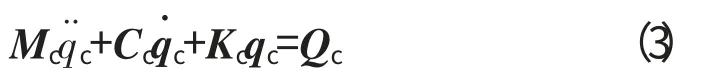
式中：Mc、Cc、Kc、Qc分別為機匣的質量矩陣、阻尼矩陣、剛度矩陣和承受的載荷，具體見表1～3。

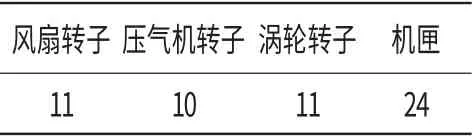
表1 轉子與機匣單元數(shù)

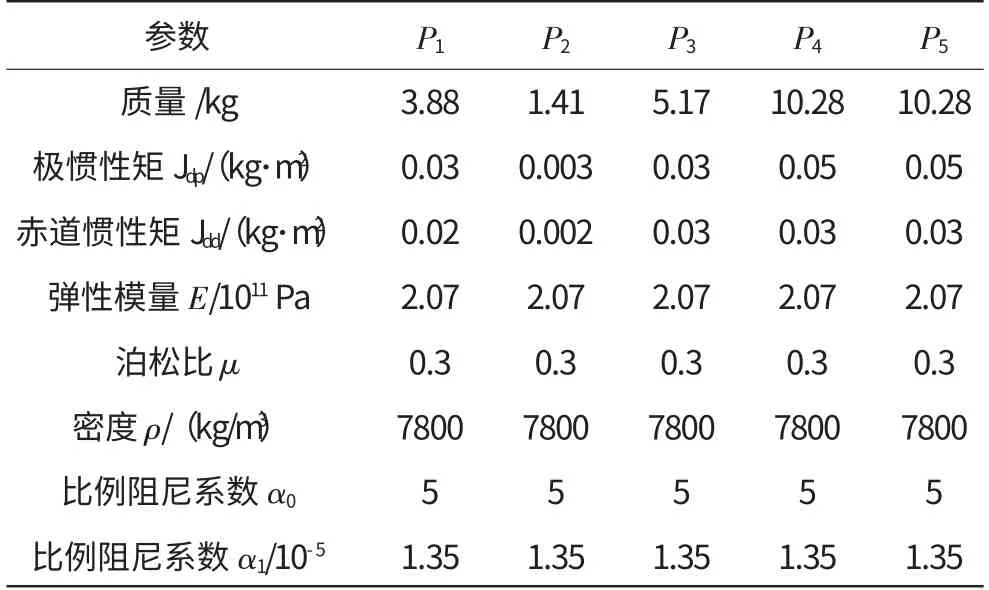
表2 轉子參數(shù)

表3 機匣參數(shù)

2.3 轉子-機匣間的支承連接

設mwi為滾動軸承外圈質量；mbi為軸承座質量；kti、cti分別為軸承外圈與軸承座之間的連接剛度和阻尼；kfi，cfi分別為機匣與軸承座之間的連接剛度和阻尼。轉子-機匣支承如圖5所示。圖中FyRi和FxRi為轉子所支承的外力；FyCi和FxCi為機匣所承受力。

本文設定軸承內(nèi)、外圈分別固定在轉軸和軸承座上。當轉子第m個節(jié)點位移為xRm和yRm，令x=xRm-xwi，可以得到轉子作用于第i個支承的軸承力

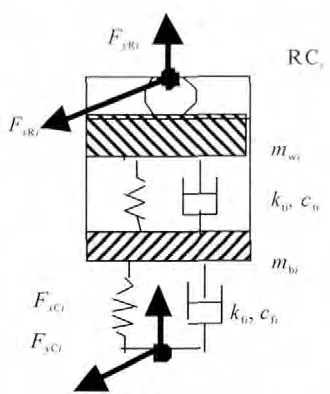
圖5 轉子-機匣支承

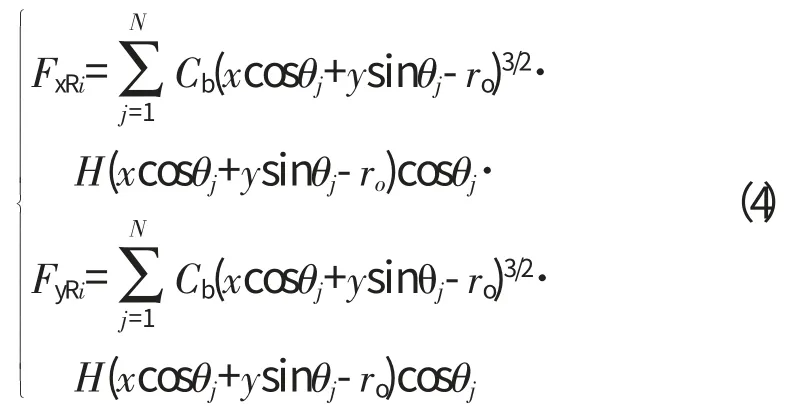
式中：Cb為赫茲接觸剛度，由內(nèi)外圈和滾珠的赫茲接觸彈性分析得到；H(·)是亥維塞函數(shù)，當函數(shù)變量大于0時，函數(shù)值是1，否則為0；θj為第j個滾珠處的角度位置其中Nb為滾珠個數(shù)；ωCage為保持架旋轉速度，設外、內(nèi)滾道半徑為R 和為轉軸旋轉角速度；ro為軸承間隙。

因此，滾動軸承外圈的運動微分方程為

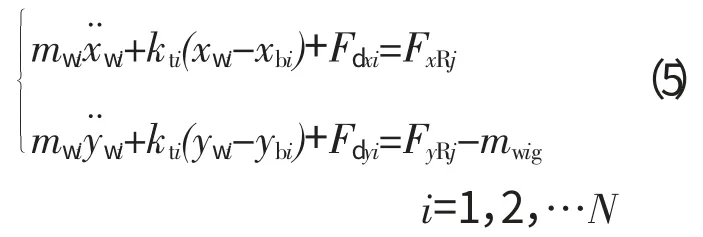
式中：Fdxi和Fdyi為阻尼力，若考慮為黏性阻尼，則

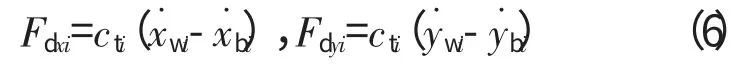
滾動軸承和轉子-機匣支承參數(shù)分別見表4、5。

2.4 轉子-機匣間的彈性連接

設轉子和機匣第i、j個節(jié)點采用彈性連接，徑向剛度為kgx、kgy，徑向阻尼為cgx、cgy，角向剛度為kgα、kgα，角向阻尼為cgα、cgα。設轉子的第i 節(jié)點的位移為xri、yri、φri、ψri速度為設機匣的第j 節(jié)點的

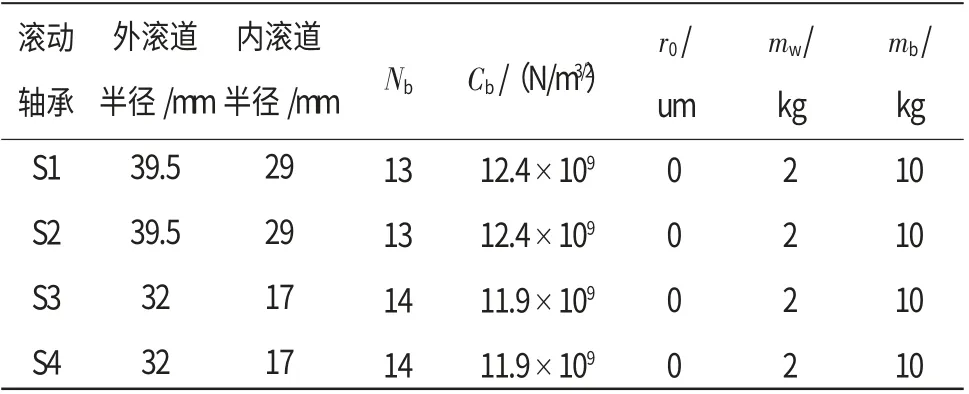
表4 滾動軸承參數(shù)

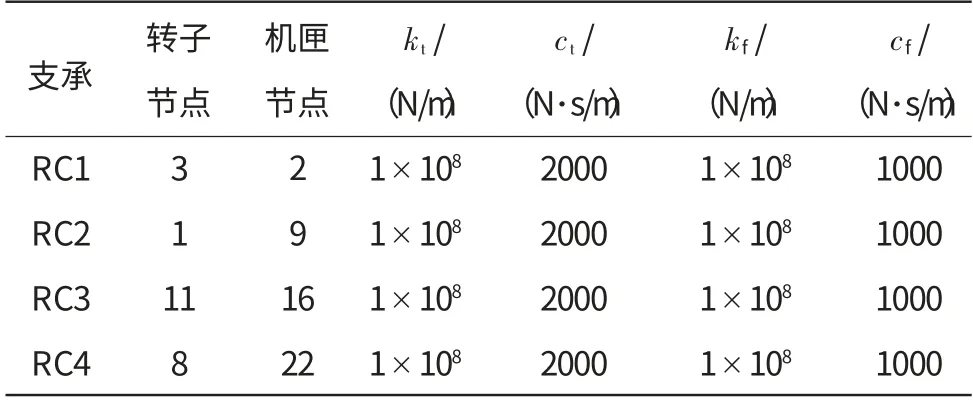
表5 轉子-機匣支承參數(shù)

位移為xri、yri、φri、ψri速度為，則作用在轉子節(jié)點i 上的力和力矩Fxi，F(xiàn)yi，Mxi，Myi，作用在機匣上的節(jié)點j 上的力和力矩Fxj，F(xiàn)yj，Mxj，Myj為

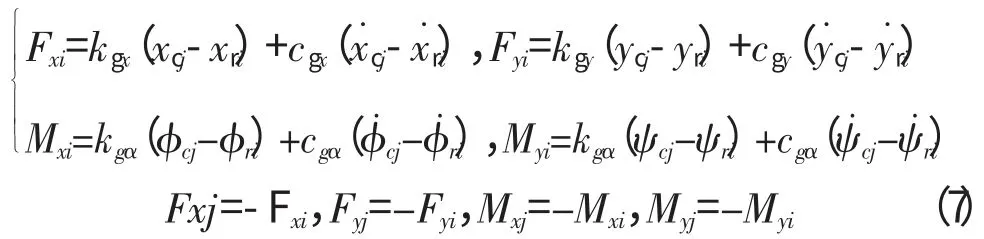
轉子-機匣連接參數(shù)見表6。

表6 轉子-機匣連接參數(shù)Tg

2.5 轉子-轉子間的聯(lián)軸器連接以及機匣-基礎間連接

左、右轉子之間的聯(lián)軸器連接參數(shù)見表7，機匣與基礎間的連接參數(shù)見表8，具體力學關系參考文獻[8]。

表7 轉子-轉子連接參數(shù)

表8 機匣-基礎連接參數(shù)

2.6 時域數(shù)值求解方法

本文采用傳統(tǒng)和改進的Newmark-β 法（新型顯示積分法-翟方法）求解，流程如圖6所示。

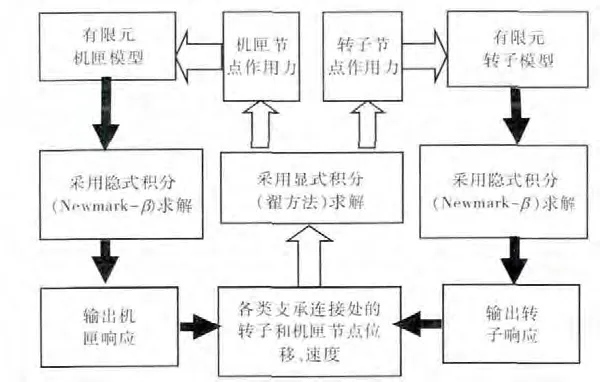
圖6 轉子-支承-機匣動力學求解流程

3 臨界轉速影響因素分析

為研究壓氣機支承剛度對整機振動的影響，改變其前、后支承剛度，分析機匣橫向臨界轉速。

不同壓氣機前支承剛度下機匣橫向加速度振幅-轉速曲線如圖7所示。在后支承剛度為1.5×108N/m條件下，4種不同剛度下的第1階臨界轉速均為21000r/min；第2階臨界轉速分別為27000r/min、31000r/min、32000r/min、34000r/min。

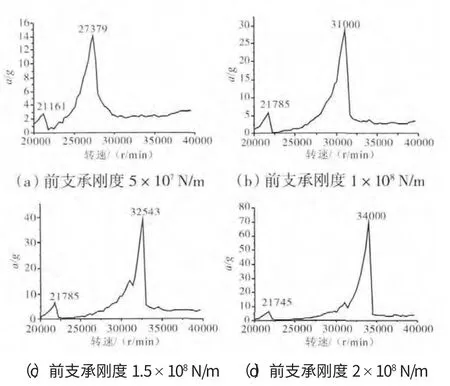
圖7 不同前支承剛度下機匣橫向加速度振幅-轉速曲線

不同壓氣機后支承剛度下機匣橫向加速度振幅-轉速曲線如圖8所示。在前支承剛度為1.5×108N/m下，4種不同剛度下的第1階臨界轉速均為21000r/min；第2階臨界轉速分別為28000、34000、32000、33000r/min。

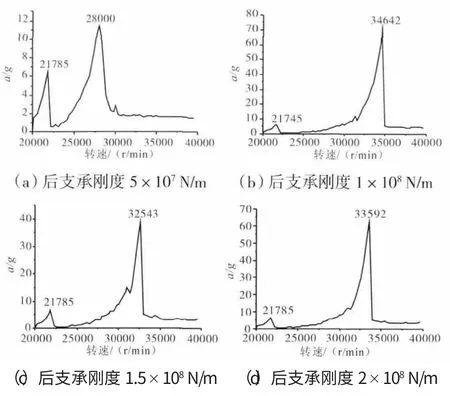
圖8 不同后支承剛度下機匣橫向加速度振幅-轉速曲線

不同臨界轉速下的振型如圖9所示。其中，（a）為第1階臨界轉速21000r/min下的渦輪轉子的俯仰振型；（b）為第2階臨界轉速31000r/min下的壓氣機轉子的彎曲振型。從圖中可見，在第2階臨界轉速下，由于前后轉子變形較大，故壓氣機前、后支承的剛度對轉子的振型影響顯著。

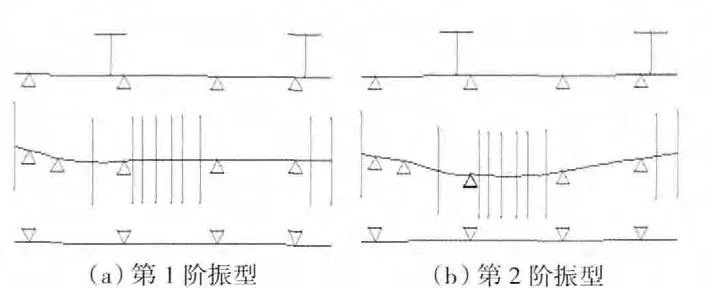
圖9 不同臨界轉速下的振型

對比實際試車數(shù)據(jù)得到的臨界轉速，并且由壓氣機前、后支承剛度對其臨界轉速影響分析可得，壓氣機前、后支承剛度均為1.5×108N/m，仿真模型和實際航空發(fā)動機相近。

仿真與試驗得到的水平測點的1倍頻隨轉速的變化曲線如圖10所示。測點為壓氣機支承對應的機匣橫向測點。從圖中可見，在轉速升高的過程中，1倍頻增加。從水平方向的振值可見，在轉速為28000r/min下，1倍頻振幅為6.5g；在轉速30000 r/min下，1倍頻振幅為19.5g。因此，仿真結果與試車數(shù)據(jù)具有良好的一致性。

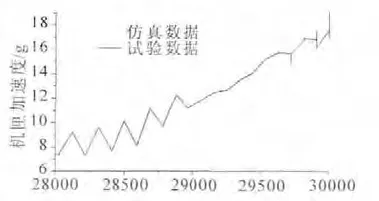
圖10 機匣橫向加速度振幅-轉速曲線

4 結論

（1）針對某彈用渦扇發(fā)動機，建立了整機振動有限元動力學模型，模型中考慮滾動軸承的非線性，及轉子與機匣之間的彈性連接。

（2）由于壓氣機前、后支承剛度對轉子的臨界轉速影響較大，所以需要控制好主要影響因素——支承剛度。

（3）從試車與仿真數(shù)據(jù)對比分析得出，在臨界轉速附近的1倍頻的振幅變化具有良好的一致性，為控制其產(chǎn)生共振提供理論依據(jù)。

[1]Chu F L，Zhang Z S.Periodic,quasi-periodic and chaotic vibrations of a rub-impact rotor system supported on oil f i lm bearings[J].International Journal of Engineering Science，1997，35（10/11）：963-973.

[2]馬輝，汪博，太興宇，等.基于接觸分析的轉定子系統(tǒng)整周碰摩故障模擬[J].工程力學，2013，30（2）：365-371.MA Hui，WANG Bo，TAI Xing-yu，et al.Full rubbing simulation of a rotor-stator system based on contact analysis [J].Engineering Mechanics，2013，30（2）：365-371.（in Chinese）

[3]張楠，劉占生，姜興渭.高速轉子軸承系統(tǒng)碰摩故障仿真研究[J].振動與沖擊，2010，29（9）：77-81.ZHANG Nan，LIU Zhansheng，JIANG Xingwei.Simulation study on rub-impact fault of high-speed rotor-bearing system [J].Journal of Vibration and Shock，2010，29（9）：77-81.（in Chinese）

[4]馬輝，李煥軍，劉楊，等.轉子系統(tǒng)耦合故障研究進展與展望[J].振動與沖擊，2012，31（17）：1-11.MA Hui，LI Huanjun，LIU Yang，et al.Review and prospect for research of coupling faults in rotor systems[J].Journal of Vibration and Shock，2012，31（17）：1-11.（in Chinese）

[5]劉楊，太興宇，趙倩，等.轉子系統(tǒng)不對中-碰摩耦合故障的動力學特性[J].東北大學學報（自然科學版），2013，34（4）：564-568.LIU Yang，TAI Xingyu，ZHAO Qian，et al.Dynamic characteristics of misalignment-rubbing coupling fault for rotor system [J].Journal of Northeastern University（Natural Science），2013，34（4）：564-568.（in Chinese）

[6]劉獻棟，何田，李其漢.支承松動的轉子系統(tǒng)動力學模型及其故障診斷方法[J].航空動力學報，2005，20（1）：54-59.LIU Xiandong，HE Tian，LI Qihan.Dynamic model of rotor system with support loosening and its diagnosis method [J].Journal of Aerospace Power，2005，20（1）：54-59.（in Chinese）

[7]馮國全，周柏卓，林麗晶，等.內(nèi)外雙轉子系統(tǒng)支撐軸承不對中分析[J].振動與沖擊，2012，32（7）：142-147.FENG Guoquan，ZHOU Baizhuo，LIN Lijing，et al.Misalignment analysis for support bearing in an inner-and-outer dual rotor system[J].Journal of Vibration and Shock，2012，32（7）：142-147.（in Chinese）

[8]陳果.航空發(fā)動機整機振動耦合動力學模型及其驗證[J].航空動力學報，2012，27（2）：242-254.CHEN Guo.A coupling dynamic model for whole aeroengine vibration and its verification[J].Journal of Aerospace Power，2012，27（2）：242-254.（in Chinese）

[9]姜廣義，王娟，姜睿.航空發(fā)動機風扇機匣振動故障分析[J].航空發(fā)動機，2011，37（5）：38-44.JIANG Guangyi，WANG Juan，JIANG Rui.Aeroengine fan casing vibration fault analysis[J].Aeroengine，2011，37（5）：38-44.（in Chinese）

[10]鄭旭東，張連祥.航空發(fā)動機整機振動典型故障分析[J].航空發(fā)動機，2013，39（1）：34-37.ZHENG Xudong，ZHANG Lianxiang.Typical failure analysis of aeroengine vibration [J].Aeroengine，2013，39（1）：34-37.（in Chinese）

[11]楊東，劉忠華.某航空發(fā)動機轉子彈性支承松動振動故障診斷研究[J].測控技術，2007，26（4）：7-13.YANG Dong，LIU Zhonghua.Diagnosis of vibration fault generated by the loose of elasticity backup bearing on aeroengine's rotor[J].Measurementand Control Technology，2007，26（4）：7-13.（in Chinese）

[12]黃慶南，楊養(yǎng)花，申秀麗，等.某型發(fā)動機渦輪轉子前、后擋板連接螺釘松動故障分析[J].航空發(fā)動機，2004，30（4）：45-47.HUANG Qingnan， YANG yanghua， SHEN Xiuli， et al.Troubleshooting of loosened front/rear retainer bolts in a typical aeroengine[J].Aeroengine，2004，30（4）：45-47.（in Chinese）

[13]可成河，鞏孟祥，宋文興.某型發(fā)動機整機振動故障診斷分析[J].航空發(fā)動機，2007，33（1）：24-26.KE Chenghe，GONG Mengxiang，SONG Wenxing.Fault diagnosis analysis of an aeroengine vibration[J].Aeroengine，2007，33（1）：24-26.（in Chinese）

[14]楊玲，王克明，張瓊.某型航空發(fā)動機整機振動分析[J].沈陽航空工業(yè)學院學報，2008，25（5）：9-15.YANG Ling，WANG Keming，ZHANG Qiong.Vibration analysis of a turbofan aeroengine[J].Journal of Shenyang Institute of Aeronautical Engineering，2008，25（5）：9-15.（in Chinese）

[15]高艷蕾，李勇，王德友.轉子-機匣系統(tǒng)碰摩故障特征試驗研究[J].航空發(fā)動機，2002（4）：16-21.GAO Yanlei，LI Yong，WANG Deyou.Experimental investigation of rotor-to-casing rubbing fault[J].Aeroengine，2002（4）：16-21.（in Chinese）