正確引領學生探究 培養良好解題策略

朱國生

摘 要：初中數學課堂要注重引導學生進行自主探究，教師就必須指導學生弄清探究的方向及內容。解題策略是學生探究的重要內容，教師應引導學生理解退中求進、以靜制動、正難則反、化零為整、挖隱為明等常見的解題策略。

關鍵詞：初中數學 探究學習 解題策略

數學課堂要引導學生通過自主探究來解決問題，教師應教會學生有效的解題方法與策略，增強探究活動的實效性。我從多年的教學工作實踐中總結了多種解題策略，有效地提高了學生的自主研究能力。

一、退中求進

華羅庚先生曾經說過：“把一個比較復雜的問題‘退到最簡單、最原始的問題，把這最簡單、最原始的問題想通了、想透了，問題就好解決了。”我想這種解決數學問題的辦法是一個非常精辟的思維方法。一個簡單的“退”，卻是為了大步地向前進。如果一直退到起點，問題也就簡單化了，再從簡單的問題中找出規律、看清本質，解題時就會化繁為簡、出奇制勝，收獲意想不到的結果。

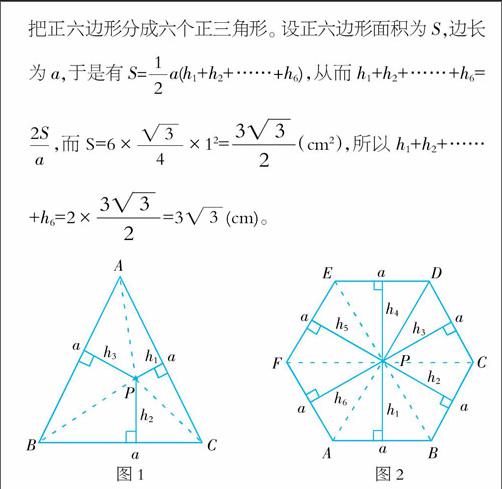
例1 已知正六邊形邊長為1 cm，P是正六邊形內一點，求P到各邊的距離之和。

分析：由于P是正六邊形內任意點，直接解答不是很容易，我們可以“退”到邊數最小的正三角形內來研究，求證三角形內一點到各邊距離之和。如圖1，在正三角形ABC中，由S△ABC=S△PAB+S△PBC+S△PA 。由此推測，本道題可以用類似方法求解，這就是退中求進的策略。

如圖2，在正六邊形ABCDEF中，連接P與各頂點，把正六邊形分成六個正三角形。

二、以靜制動

世間沒絕對的靜止，運動才是現實的。在解決數學中的運動問題時，有時以靜制動也是一個重要的解題策略。

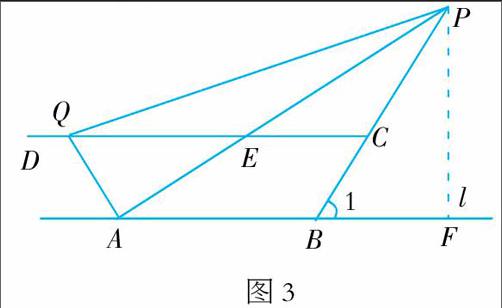
例2 如圖3，A，B是直線l上的兩點，AB=4 cm，過外一點C作CD∥l，射線BC與l所成的銳角∠1=60°，線段BC=2 cm，動點P，Q分別從B，C同時出發，P以1 cm/s的速度由B向C的方向運動，Q以2 cm/s的速度由C向D的方向運動。設P，Q運動的時間為t，當t>2時，PA交CD于E，求解下列問題。

（1）用含t的代數式分別表示CE和QE的長;

（2）求△APQ的面積S與t的函數關系式;

（3）當QE恰好平分△APQ的面積時，QE的長是多少？

分析：在運動過程中不要被點的運動所迷惑，而要在運動中找出不變的量或比例關系，以靜制動。第（1）問，無論t怎么變化， 的比例關系都沒有變化，這就容易求得CE，QE的表達式。第（3）問，由于QE平分△APQ的面積，我們可推斷AE=PE，此時C為PB的中點。

題解：（1）依題意，可得BP=t，CQ=2t，PC=t-2

三、正難則反

在探討某一問題的解決辦法時，有時使用逆向思維較使用正向思維見效更快。當正面思考遇到困難時，就“反其道而求之”，常有“峰回路轉”之奇效。

例3 若函數 的自變量x的取值范圍是一切實數，則c的取值范圍是（ ?）。

A.c>1 ? B.c=1 ? C.c<1 ? D.c≤1

分析：此題綜合了很多知識點，由分母x2+2x+c≠0來求字母系數c的取值范圍，這是很難求得的。若變換角度研究，從反面考慮x2+2x+c≠0的意義就是x2+2x+c=0無實數解，這樣就把問題與方程的系數聯系起來了，顯然由Δ=22-4c<0得c>1，故選A。

四、化零為整

有些數學問題分局部考慮，不勝其“繁”，抑或難以下手，但化零為整，不僅可以避繁就簡，還可以使問題迎刃而解，這種解題策略值得我們借鑒。

例4 如圖4，在高2米，坡角為30°的樓梯表面鋪地毯，地毯的長度至少需要多少米？

分析：如果先把鋪在各個小臺階上的地毯長度和高度求出，再求和，這顯然不是明智之舉。如果臺階的級數未知，那更是無從下手。通過化零為整策略可知，平移各小臺階，其高度之和就是BC長，寬度之和就是AC長，求出線段BC，AC長度，其和的問題就迎刃而解了。

五、挖隱為明

數學試題中的隱含條件是指數學題目中的那些不易被察覺，但又直接影響解題思路甚至解答結果的已知條件。許多學生在解題時，往往忽視對隱含條件的把握，出現錯解誤證，甚至解不出來的現象。如能明確隱含條件的隱含形式，引導學生挖掘題中的隱含條件，這對解決含有隱含條件的問題將大有幫助。

例5 如圖5，二次函數y=ax2+bx+c的圖像，在下列6個代數式ab，ac，a+b+c，a-b+c，2a+b，2a-b中，其值為正值的式子個數為（ ? ）。

A.2個 ?B.3個 ?C.4個 ?D.4個以上

分析：本題只有一個特定位置的拋物線，觀察這一特定位置，隱含了拋物線的一些特點，包括開口向下，與y軸交點在下方，頂點橫坐標大于0且小于1，x=1時y>0，x=-1時y<0等。

簡解：已知a<0，c<0故ac>0;x=1時y>0，即a+b+c>0;x=-1時y<0，即a-b+c<0;0<-<1，即2a+b<0;由a<0知b>0，從而ab<0，2a-b<0，所以，歸納出值為正的式子有兩個。故選A。

在數學教學中，我們不但要對學生加強必要的訓練，還要教會學生掌握一定的解題策略與方法。引導學生在解題時，要多角度考慮解題的途徑，培養學生的數學領悟力。這種學習方法的掌握和思維能力的提升對今后的學習和實際問題的解決都大有幫助。

參考文獻

[1]宋蓓.初中數學解題策略的研究及應用[D].天津：天津師范大學，2013.

[2]張文宇.初中生數學學習選擇能力研究[D].濟南：山東師范大學，2011.

[3]陳建勇.例析初中數學解題策略[J].數理化解題研究（初中版），2013（7）.