基于數據驅動的動車組齒輪箱在線故障預報*

王　鋒， 張　兵， 林建輝

（西南交通大學牽引動力國家重點實驗室 成都，610031）

?

基于數據驅動的動車組齒輪箱在線故障預報*

王鋒， 張兵， 林建輝

（西南交通大學牽引動力國家重點實驗室 成都，610031）

齒輪箱作為高速動車組的關鍵部件之一，其工作性能直接影響到高速動車組運行的可靠性和安全性。動車組齒輪箱結構復雜，且在實際運行中可能受到很多外界因素的激擾，難以建立合適的動力學模型。筆者介紹了一種檢測高速動車組齒輪箱故障的時間序列算法，該方法基于數據驅動，不需要建立動力學模型，適合在線故障預報。無線微機電傳感器從齒輪箱測得加速度信號并建立時間序列模型，利用模型的自回歸參數定義故障敏感參數（FSP）。在有故障和無故障兩種狀態下，FSP均值完全不同。通過比較FSP均值，然后用假設檢驗中的t檢驗判定是否存在故障。實踐證明，筆者提出的方法能較好地在線識別高速動車組齒輪箱早期故障，具有重要的應用意義。

時間序列；ARMA模型；故障敏感參數；t檢驗

引 言

隨著列車運營速度的不斷提升，高速列車的運行安全性和可靠性研究變得越發重要。作為高速動車組動力傳遞的關鍵部件，齒輪箱的任何細小故障都可能引發重大安全事故。為進一步完善高速動車組安全運營相關理論，急需開展對高速列車齒輪箱的故障預報研究。

當前齒輪箱的故障診斷方法很多，如振動診斷［1］、噪聲分析［2］、扭振分析［3］、油液分析［4］、聲發射［5］、溫度［6］及能耗監測［7］等。高速動車組是一個非常復雜的非線性系統，其動力分散，具有大編組和高速化等特點。考慮高速動車組的實際運行特點，常見的動車組齒輪箱故障診斷，多是基于振動、溫度和噪聲的測試分析［8］。動車組齒輪箱結構復雜，且在實際運行過程中由于輪軌間的非線性耦合關系，可能受到各種外界因素的激擾，難以建立合適的動力學模型。而且，系統建模方法涉及有限元建模，系統辨識的計算過程復雜，無法實現在線故障預報。

為了解決上述問題，筆者提出了一種基于數據驅動的檢測動車組齒輪箱故障的時間序列算法。該方法基于黑箱理論，不需要建立動力學模型，適合在線診斷及故障預報。在有限的安裝空間，利用低功耗無線微機電傳感器（micro electro-mechanism sensor，簡稱MEMS）組成密集的無線傳感網絡，MEMS從齒輪箱測得加速度信號并建立時間序列模型，通過無線網絡回傳模型的特征參數，利用特征參數來定義故障敏感參數（fault sensitive parameters，簡稱FSP）。在有故障和無故障兩種狀態下，FSP的均值完全不同。通過比較FSP均值，然后用假設檢驗中的t檢驗判定是否存在故障。通過決策層多傳感器數據融合，判定齒輪箱故障狀態。實踐證明，筆者提出的方法可以較好地識別高速動車組齒輪箱早期故障，具有重要的實際應用意義。

1 試驗方案及數據預處理概述

動車組整車試驗系統由無線數據采集系統、列車級檢測系統、地面數據處理系統、遠程監控中心等4個子系統組成。圖1為試驗系統的組成結構圖。

無線數據采集系統由傳感器（振動、動應力、溫度、壓力等）、調理器、采集器和ZigBee網絡組成，功能為采集測點的位移、加速度、應變、溫度和壓力等物理量，將采集信號存儲在微型大容量的采集卡中，計算物理量的特征參數（均值、最大值、變化率、主頻等）并將特征參數通過ZigBee無線網絡傳輸到列車監測系統中。

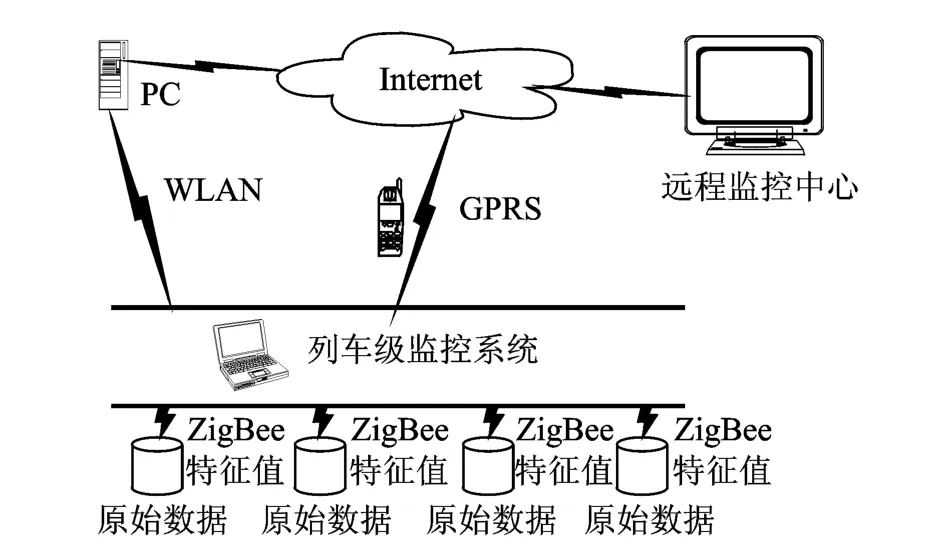
圖1　跟蹤試驗系統的組成結構圖Fig.1 Schematic diagram of sensor on gearbox

列車級檢測系統主要由采集器、交換機、車載電腦、3G路由和GPS（測速模塊）構成，車載電腦通過車內局域網對整個采集系統進行控制。

地面數據處理系統設在動車所或檢修基地，由地面主機和無線接入器組成，負責入庫后列車級監測系統的數據下載，對數據進行初步處理，為動車段提供數據異常信息等，便于進行檢修。

遠程監控中心利用GPRS網絡實時傳輸過來的動車組高速運行時列車級監測系統的數據，遠程時空同步監控動車組關鍵部件的工作狀態，同時對數據進行綜合分析處理，提供列車的狀態特性，完成各種歷史數據的對比分析。

遠程監控中心利用GPRS網絡，實時傳輸動車組高速運行時列車級監測系統的數據，遠程時空同步監控動車關鍵部件的工作狀態，同時對數據進行綜合分析處理，提供列車的狀態特性并完成各種歷史數據對比分析。

圖2給出了某列動車組跟蹤試驗中齒輪箱位置的傳感器布置示意圖。

圖2　齒輪箱測點傳感器布置示意圖Fig.2 Schematic diagram of sensor on gearbox

為了實現不同類型數據的比較，保證模型的通用性，需要對傳感器測得的原始數據進行預處理。數據預處理包括異點剔除［9］、趨勢項消除［8］、歸一化處理等。對于第i個傳感器測得的信號xi（t），其歸一化信號可由下式獲得：

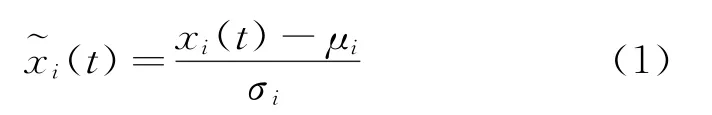
其中：μi和σi分別為xi（t）的均值和標準差。

2 故障預報原理

動車組實際運營過程中可能受到很多隨機因素的影響，理論上講，一列在平穩線路上正常行駛的動車組，其測得信號（加速度、溫度等）應為隨機時間序列。測得數據包含4個方面的信息：a.序列本身的結構與規律，或者說，相應系統的行為特性；b.相應系統本身的固有屬性（即系統的結構與參數），這一固有屬性同外界作用無關；c.外界對系統的輸入；d.相應系統同外界聯系的方式，即外界以什么方式對系統施加輸入。

動車組齒輪箱在故障前期的初始表現往往是振動異常，因為故障會影響齒輪箱的結構動態特性，導致測得的振動加速度信號的統計特性隨時間歷程而改變。因此，可以通過時間序列分析故障前后測得的加速度信號，識別齒輪箱早期故障（包括電蝕、齒面磨損、齒面剝落、齒根裂紋以及箱體疲勞等）。當設備狀況持續惡化過程中，可用不同的探測技術監測動車組齒輪箱的運行狀態。

動車組齒輪箱整個生命周期的狀態監測方法如圖3所示。

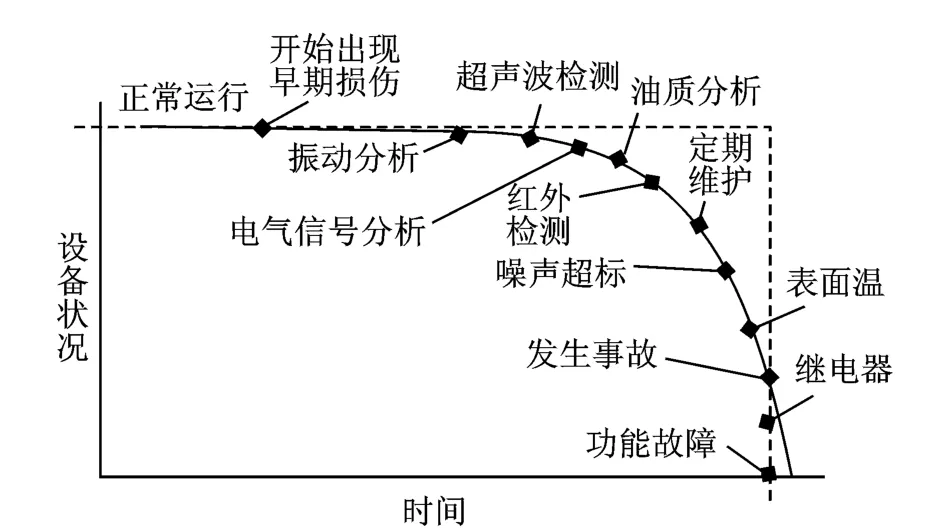
圖3　動車組齒輪箱狀態監測方法Fig.3 The condition monitoring method of the gearbox

3 故障預報算法

3.1時間序列建模

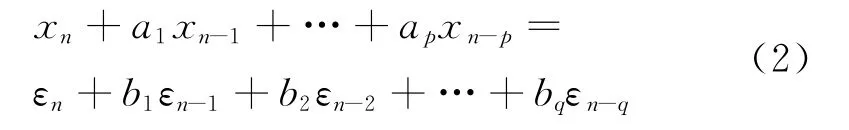
數據預處理完成后，可以用來進行時序建模。一個ARMA（p，q）過程的一般形式［10］為其中：ap為自回歸系數；bq為滑動平均系數；εn為白噪聲激勵，εn的均值為0，方差為σ2ε。

當q=0時，式（2）表示一個純自回歸模型，記為AR（p）；當p=0時，式（2）表示一個純滑動平均模型，記為MA（q）。一個有連續譜密度函數的平穩隨機過程，可以表示為一個確定AR（∞）或MA（∞）隨機過程。時序建模的過程即確定模型階次p，q和模型參數ap，bq的過程。

建立準確的時間序列模型，是正確預報故障的關鍵。通過選擇合適的判定函數以及比較不同類型時序模型之間的預測誤差［11-12］，可以實現數據的自適應時序建模［13］，自動選擇最佳的模型類型（AR模型、MA模型或ARMA模型），并確定模型的最佳階次。自適應時序建模流程圖如圖4所示。

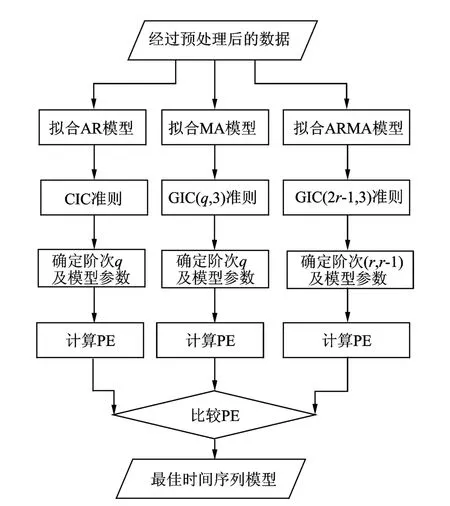
圖4　算法流程圖Fig.4 Flowchart of the algorithm

分別根據CIC準則選擇最優的AR（p）模型、根據GIC（q，3）準則選擇最優的MA（q）模型、根據GIC（2r-1，3）準則選擇最優的ARMA（r，r-1）模型后，3個模型的預測誤差可以通過給定時序進行估計。MA模型和ARMA模型的預測誤差為

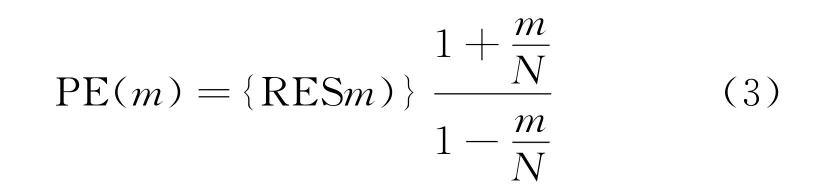
其中：m為模型中的參數個數，RES（m）為模型殘差。

對于AR（p）模型，其預測誤差為

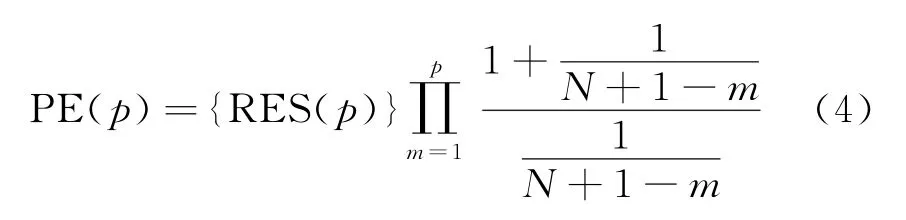
在估計參數數量大于N/10時，式（4）得出的結果與式（3）有顯著差異。通過比較兩式的結果，可以自動識別預測誤差最小的模型，實現了自適應建模的目的。

3.2ARMA模型參數敏感性分析

時間序列模型的AR系數中包含關于系統模態固有頻率和阻尼比的信息。在有輸入信號（假設為白噪聲）時，ARMA模型可被視為帶外源輸入時序（ARX）的自回歸模型，該模型可用z變換的時移特性在復數z域檢查。

關于?α2/?θi和?α3/?θi的關系推導與此相同。

由上可得，當齒輪箱發生故障時，必然會導致其剛度變化，同時帶來其響應的改變和基于響應建立的時序模型AR系數的改變。因此，基于AR系數的FSP參數可以測得這種變化并預報齒輪箱故障。

3.3故障敏感參數（FSP）

根據上面得到的最佳時序模型，可有效識別齒輪箱特征參數。經過自適應建模的時序模型，其AR參數表征動車組齒輪箱的固有特性，MA參數表征外界隨機激勵。當發生故障時，部分特征參數會發生改變。但并非所有特征參數都對故障敏感，將在有故障和無故障兩種狀態下存在顯著差異的時間序列模型特征參數或其組合定義為故障敏感參數（FSP）。

選取FSP的基本原則：a.獨立性：對速度等頻繁變化的外界因素不敏感；b.相容性：最好是無量綱量，方便不同傳感器數據融合；c.穩定性：同一狀態下不應該發生劇烈改變，滿足正態分布特征，其變動范圍以不超過全局極大值和極小值差值的一半為宜；d.完備性：在有故障和無故障兩種狀態下，FSP值應該發生顯著變化。

在對比動車組齒輪箱加速度歷史數據并計算幾組不同的FSP之后發現，對動車組齒輪箱早期故障而言，時序ARMA模型的前3階AR系數的統計意義最為顯著。由此定義早期故障的FSP為

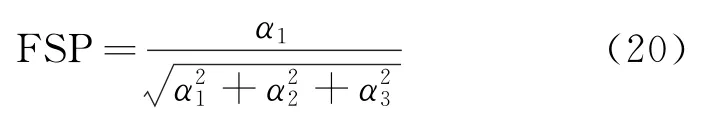
其中：α1，α2，α3分別為時序模型的前3個AR系數。

3.4故障判定方法

直接采信被觀測對象功能及性能信息的特征參數改變進行故障診斷，是置信度最高的故障診斷方法。但是，除了故障診斷算法本身的設計問題外，由于車上與實驗室工作應力和環境應力的不同，使得車上測試狀態與地面復測狀態存在差異，可能導致虛警率較高［13-14］。由此引入假設檢驗方法，提高故障判定的準確率。

用μFSPd和μFSPu分別代表有故障和無故障兩種狀態下FSP參數的均值，建立如下假設：

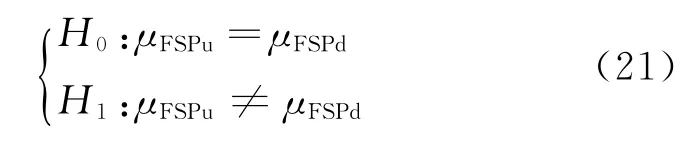
其中：H0和H1分別為無效假設和備選假設。H0代表無故障狀態，H1代表故障狀態。顯著性水平設為0.05。

4 動車組齒輪箱故障預報實例分析

在跟蹤試驗中，為了監控齒輪箱的運行狀態，在齒輪箱上部和下部均安裝了三向加速度傳感器，測試相對列車行進方向的橫向、縱向和垂向加速度，采樣頻率為2 k Hz。下面以動車組齒輪箱早期故障為例，說明故障預報的過程。

隨意截取某次試驗某個測點在不同速度下的5段數據進行分析（編號為xi，i=1，2，3，4，5），每段數據的長度為4 000點（采樣時間2 s）。首先對這5段數據進行異點剔除、趨勢項消除和歸一化預處理，預處理后的加速度數據如圖5所示。

接下來對這些數據進行自適應建模分析，并檢驗模型的適用性，判斷模型的穩定性。實際應用過程中，最為關鍵的是選取合適的時序模型及其階次，同時確定最佳的分析點數。將每段數據分為j個長度為n的子段（編號為xij，其中i=1～5，j=1～4 000/n），對每個xij進行自適應建模。按照同樣的方法建立所有子段的模型后，分析模型前三階AR系數的均值和方差，依此判斷模型是否穩定，從而得到最佳的建模數據點數。對其中一段數據分析的結果如表1所示（μαi表示特征參數αl的均值，σαl表示特征參數αl的方差，l=1，2，3），其余4段的分析過程與此相同。

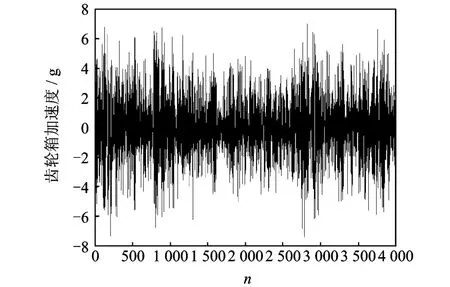
圖5　經過預處理后的加速度數據Fig.5 The acceleration data after preprocessing

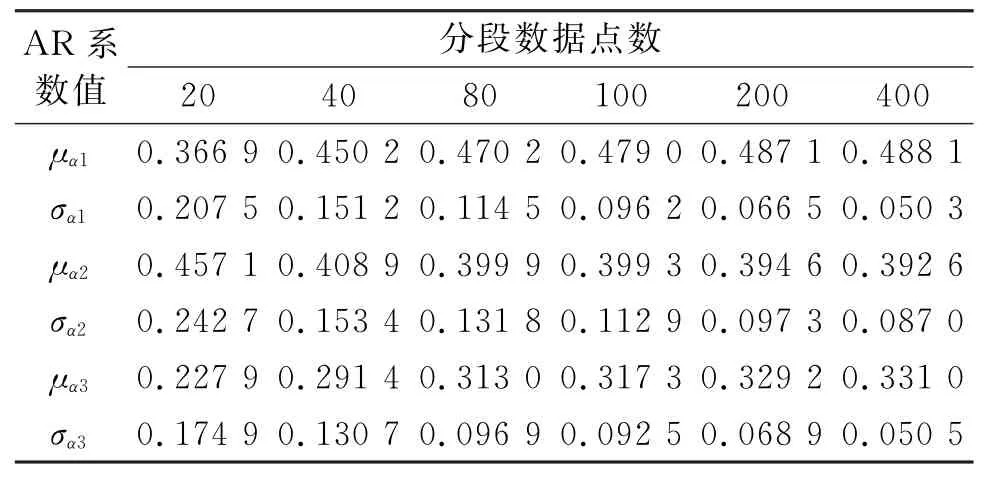
表1　AR系數相對于數據點數量的敏感性Tab.1 Sensitivity of AR coefficients to the number of data points

從表1可以看出，前3階AR系數在100點時基本穩定。為了在模型穩定性和故障預報實時性之間取得平衡，實際計算時取200點分段長度的子段進行分析。隨意選取其中一個長度為200點的子段進行自適應建模如圖6所示。從圖6可以看出，估計誤差最小的適用模型為AR（15），與自適應建模算法得出的結果一致。在確定模型穩定且對故障敏感的數據長度后，對每一小段的數據進行自適應建模并計算FSP值，結果如圖7所示。從圖中可以看出，5段數據FSP的均值發生了明顯變化。如果第1，2段數據處于正常狀態，那么第3，4，5段數據所在時間點出現齒輪箱狀態異常的概率很大。為了提高故障預報的準確率，用t檢驗判斷故障狀態。計算結果為0.001 4，即在置信度為99.86的范圍內，接受兩者均值不同的假設。即從第3段數據所在時間點開始，存在齒輪箱出現早期故障的可能。

對所有傳感器用相同方法計算FSP并作t檢驗，然后將計算結果進行決策層數據融合之后可以判定：從第3段數據所在時間點開始，齒輪箱出現早期故障。與停車檢修記錄相符，證明了所述方法的有效性。

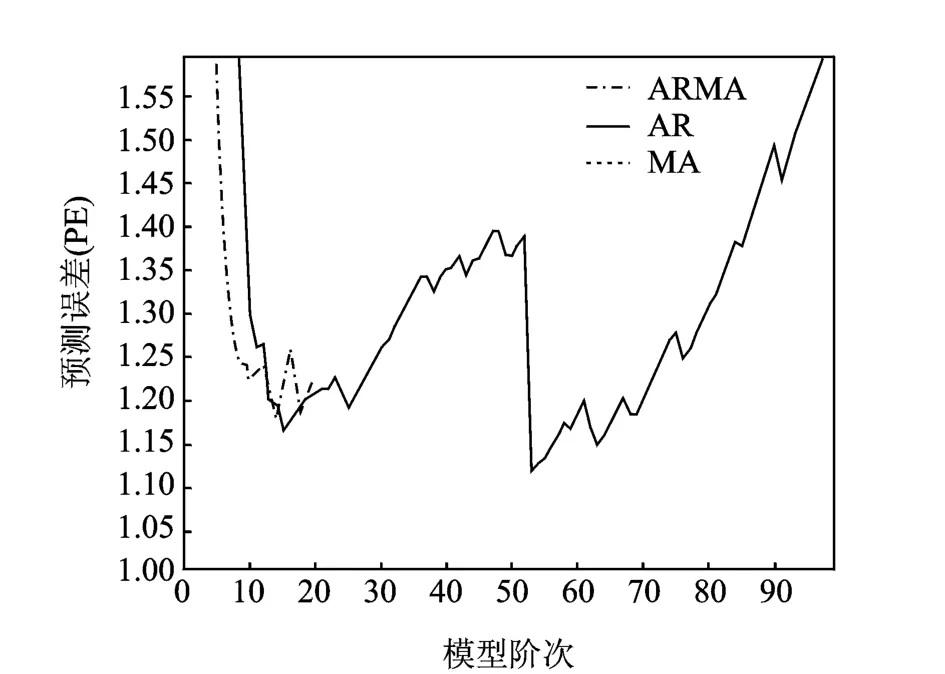
圖6　估計準確率與模型類型和階次的關系Fig.6 Estimated model accuracy as a function of the model type

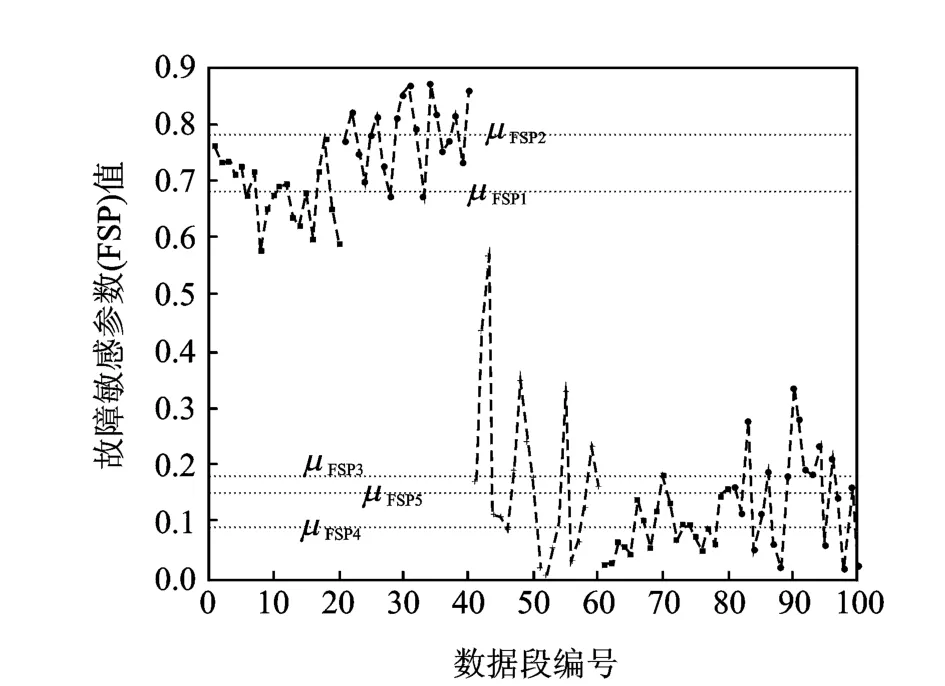
圖7　不同數據段的FSP值Fig.7 Estimated model accuracy as a function of the model type

5 結束語

筆者提出了一種基于數據驅動的動車組齒輪箱故障預報方法。該方法模型簡單，可以有效識別齒輪箱早期故障，適用于動車組齒輪箱在線故障預報，具有重要的實際應用意義。

［1］ 田濤，丁康.希爾伯特變換及其在故障診斷中的應用［J］.振動與沖擊，1996，15（2）：24-27，14，102. Tian Tao，Ding Kang.Hilbert transform and its application in the failure diagnosis［J］.Journal of Vibration and Shock，1996，15（2）：24-27，14，102.（in Chinese）

［2］ 任明章，連小珉，蔣孝煜，等.齒輪箱噪聲故障診斷專家系統的研究與開發［J］.清華大學學報：自然科學版，1996，36（8）：66-71. Ren Mingzhang，Lian Xiaomin，Jiang Xiaoyu，et al. Research and development of a diagnostic expert system for gearbox noise［J］.Journal of Tsinghua University：Sci&Tech，1996，36（8）：66-71.（in Chinese）

［3］ 樊可清，屈梁生.基于扭振信號的齒輪故障診斷研究［J］.中國機械工程，1999，10（4）：430-433. Fan Keqing，Qu Liangsheng.Diagnosing gears defect with torsional vibration signal［J］.China Mechanical Engineering，1999，10（4）：430-433.（in Chinese）

［4］ 李臻，荊雙喜，冷軍發，等.油液分析技術在齒輪減速箱故障診斷中的應用［J］.煤礦機電，2003，27（3）：27-29. Li Zhen，Jing Shuangxi，Leng Junfa，et al.The Application of oil analytic technique in fault diagnosis of gearbox［J］.Colliery Mechanical&Electrical Technology，2003，27（3）：27-29.（in Chinese）

［5］ 于洋，趙年偉，楊平，等.齒輪磨損故障聲發射檢測研究［J］.機械傳動，2013，37（4）：44-48. Yu Yang，Zhao Nianwei，Yang Ping，et al.Research on the gear wear failure based on Acoustic emission detection［J］.Journal of Mechanical Transmission，2013，37（4）：44-48.（in Chinese）

［6］ 屈文濤，沈允文，徐建寧，等.雙圓弧齒輪傳動的溫度場和熱變形分析［J］.石油機械，2006，34（3）：13-15，19. Qu Wentao，Shen Yunwen，Xu Jianning，et al.Analysis on temperature tield and thermal deformation of double-arc gear drive［J］.China Petroleum Machinery，2006，34（3）：13-15，19.（in Chinese）

［7］ 謝小鵬，馮偉，黃敦烈，等.基于能量耗損的摩擦學系統狀態識別方法研究［J］.潤滑與密封，2010，35（2）：27-31. Xie Xiaopeng，Feng Wei，Huang Dunlie，et al.Study on state recognition method of tribological system based on energy loss［J］.Lubrication Engineering，2010，35（2）：27-31.（in Chinese）

［8］ 丁福焰，杜永平.機車車輛故障診斷技術的發展［J］.鐵道機車車輛，2004，24（4）：24-29. Ding Fuyan，Du Yongping.Development of fault diagnosis technology for locomotive and car［J］.Railway Locomotive&CAR，2004，24（4）：24-29.（in Chinese）

［9］ 段虎明，謝飛，張開斌，等.海量道路路面測量數據的若干預處理方法研究［J］.振動與沖擊，2011，30（8）：101-106，117. Duan Huming，Xie Fei，Zhang Kaibin，et al.Methods of signal pre-processing with massive road surface measurement data［J］.Journal of Vibration and Shock，2011，30（8）：101-106，117.（in Chinese）

［10］Priestley M B.Spectral analysis and time series［M］. New York：Academic，1981.

［11］Broersen P M T.Selection of type and order of time series models［C］∥Proceedings of the 38th IEEE Conference.Phoenix，AZ：IEEE，1999，5：5064-5069.［12］Broersen P M T.Finite sample criteria for autoregressive order selection［J］.IEEE Trans Signal Processing，2000，48：3550-3558.

［13］Broersen P M T.Facts and fiction in spectral analysis［J］.IEEE Transactions on Instrumentation and Measurement.2000，49：766-772.

［14］曾聲奎，Pecht M G，吳際，等.故障預測與健康管理（PH M）技術的現狀與發展［J］.航空學報，2005，26（5）：626-632. Zeng Shengkui，Pecht M G，Wu Ji，et al.Status and pers pectives of prognostics and health management Technologies［J］.Acta Aeronautica Et Astronautica Sinica，2005，26（5）：626-632.（in Chinese）

TH17；U298.1

10.16450/j.cnki.issn.1004-6801.2015.02.005

王鋒，男，1979年10月生，博士生，助理研究員。主要研究方向為鐵路機車車輛設計安全檢測技術和試驗研究、信號分析與處理。曾發表《基于光纖陀螺的高速列車軌跡無線測試儀》（《計算機測量與控制》2012年第20卷第11期）等論文。

E-mail：wf@xnjd.com.cn

*“十一五”國家科技支撐計劃資助項目（2009BAG12A01-E03）、四川省科技廳資助項目（2011S20007）、高等學校博士學科點專項科研基金資助項目（2012G04005）

2013-11-25；

2014-11-30