軸承故障聲發射信號多頻帶共振解調方法*

張曉濤， 唐力偉， 王　平， 鄧士杰

（軍械工程學院火炮工程系 石家莊，050003）

?

軸承故障聲發射信號多頻帶共振解調方法*

張曉濤， 唐力偉， 王平， 鄧士杰

（軍械工程學院火炮工程系 石家莊，050003）

軸承故障聲發射信號具有高頻率、寬頻帶、多頻率成分組成特性。針對軸承故障聲發射信號的多頻帶共振解調問題，基于故障先驗知識確定濾波帶寬，利用窄帶解調Protrugram算法迭代搜索多個可解調中心頻率，在對應的多個窄帶范圍內實現故障頻率的解調識別。仿真和實驗信號處理結果表明，窄帶包絡解調方法能夠找到多個可用解調窄帶，對應解調包絡譜中均可清楚地識別故障頻率，且包絡譜具有故障頻率譜線清晰，倍頻成分衰減明顯的特點。

聲發射；多頻帶解調；Protrugram算法；故障診斷

引 言

聲發射（acoustic emission，簡稱AE）技術為軸承故障診斷提供了一種高靈敏度檢測方法［1-2］。軸承故障的聲發射信號具有高頻寬帶特點，且微弱故障信號噪聲干擾嚴重，從原始信號中提取有用信號，解調故障頻率是軸承故障聲發射診斷研究的熱點內容［3］。

聲發射信號故障傳統解調方法在寬帶濾波范圍內進行，往往包含多個沖擊共振頻率，解調結果中倍頻幅度大，且寬帶濾波解調引入更多噪聲，強故障信號識別效果較好，微弱故障識別效果不佳［2］。根據聲發射理論，軸承故障過程產生的聲發射信號由多個頻率成分組成［4］，故障沖擊共振頻率是在聲發射頻帶范圍內的一系列頻率成分，聲發射信號的多頻率成分特性使故障特征在多個共振頻率處的解調成為可能，多頻帶共振解調需要限制濾波帶寬，避免一個濾波帶寬中包含多個臨近故障共振頻率。

筆者利用窄帶包絡解調思想，根據故障先驗知識確定濾波帶寬，通過濾波信號包絡譜峭度極大值搜索可用濾波中心頻率，從而利用多個有效窄帶濾波信號解調識別故障頻率，結合仿真信號與試驗數據驗證了故障聲發射信號多頻帶共振解調的有效性，說明窄帶包絡解調方法能夠實現故障多頻帶共振解調。

1 多頻帶共振解調

齒輪箱軸承常見故障為表面損傷和疲勞磨損，運轉過程中的軸承故障由于臨界裂紋擴展、裂紋面閉合與磨損、碰撞摩擦等原因產生聲發射信號［5］。金屬材料的聲發射信號是一種高頻寬帶信號，常見金屬材料的聲發射信號頻帶處于100～500 k Hz的超聲范疇［6］。實際的故障過程很難產生帶寬特別窄帶的信號，更是幾乎不可能產生單一頻率信號［7］。聲發射相關理論表明，材料在負載作用下產生的是頻率和模式豐富的導波信號，因而故障聲發射信號包含一組頻率成分，由多頻率成分構成［8］。

復雜的頻率成分特性使故障聲發射信號具有多共振頻率解調特性，并且故障沖擊時域時間短，頻域能量分布寬，將會增強窄帶濾波的解調效果。故障聲發射信號中的多個共振頻率成分能量大小不同，且由于系統傳遞特性的影響，各個頻率成分的能量差異較大，不同故障的可解調共振頻帶并不完全相同，但都處于聲發射信號的頻率范圍內。故障信號以調制形式出現，故障多頻帶共振解調要求解調帶寬要窄，窄帶濾波信號中不能包含多個明顯共振頻率，同時又必須涵蓋故障特征頻率成分。

共振特征解調技術要求濾波器中心頻率（center frequency，簡稱CF）與故障共振頻率相近，并且濾波帶寬（bandwidth，簡稱BW）能夠包含低頻故障調制成分。已知故障頻率為fr的情況下，濾波器帶寬應盡可能小一些，避免引入過多的背景干擾噪聲。理論上濾波帶寬fr≤BW＜2fr時，濾波信號解調包絡譜中只包含一階故障頻率譜線，實際中由于濾波器邊緣特性的影響，帶寬選擇應該大一些，比如3fr＜BW＜5fr，這樣窄帶濾波后信號的解調包絡中故障頻率成分將不超過前5階倍頻成分。因此在故障多頻帶共振解調中，濾波帶寬根據軸承故障頻率選擇，取故障頻率的3～5倍，使解調包絡譜中僅含有故障頻率譜線及其前3～5倍頻成分譜線，并且解調包絡譜中包含過多的故障倍頻成分，并不能提供額外的故障信息且會導致故障頻率識別混淆［9］，窄帶解調對故障特征獲取是具有積極意義的。濾波帶寬確定之后，多共振解調中心頻率可以通過Protrugram算法迭代求解。

2 窄帶解調Protrugram算法

Protrugram算法思想最早由Tomasz與Adam提出用于低頻的振動信號處理，是一種固定帶寬濾波，迭代搜索尋找解調中心頻率的方法［9-10］。通過濾波信號包絡譜峭度值對濾波信號進行評價［11］，峭度極大值對應解調中心頻率。

該算法基于fft濾波，篩選保留固定帶寬BW的頻譜值，其余置零，經過雙邊譜重構后做ifft變換得到窄帶濾波信號，窄帶信號包絡譜基于Hilbert方法得到，窄帶信號包絡譜的計算如圖1所示。

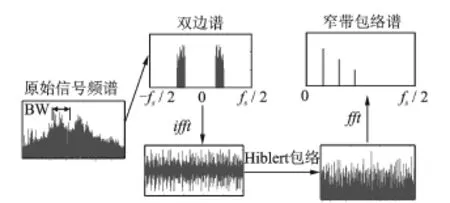
圖1　窄帶包絡計算示意Fig.1 Narrowband envelop spectrum

解算前首先確定濾波帶寬BW，和迭代步長step，由此可得中心頻率的迭代搜索范圍如式1所示，對應的算法原理如圖2所示。迭代步長step最小為信號頻域分辨率，step最大不超過BW，以保證迭代搜索能夠覆蓋整個信號頻帶，step越大，算法迭代速度越快。

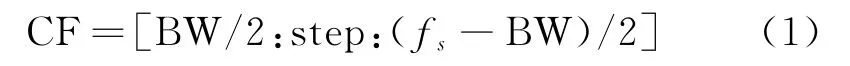
軸承故障多頻帶共振解調時，選定算法初始參數BW和step后，利用Protrugram算法計算得到中心頻率與窄帶濾波信號包絡譜峭度值的曲線，故障聲發射信號的多個解調中心頻率，對應著結果曲線的多個局部極大值。通過曲線的局部極大值確定有效的多個共振解調中心頻率，配合BW獲得多個窄帶濾波信號，計算包絡譜進行故障診斷，多頻帶共振解調的故障診斷流程如圖3所示。

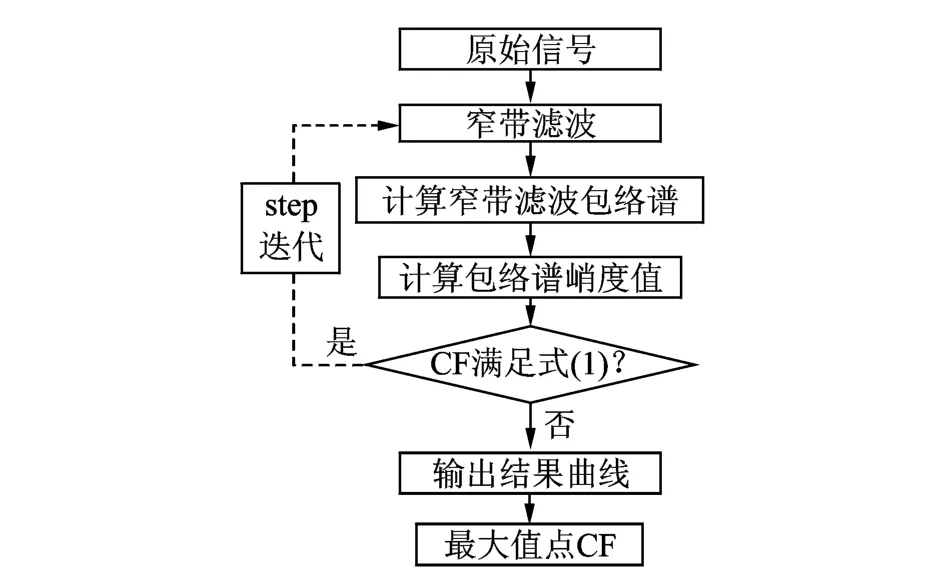
圖2　窄帶解調算法流程Fig.2 Flow chart of narrowband demodulation

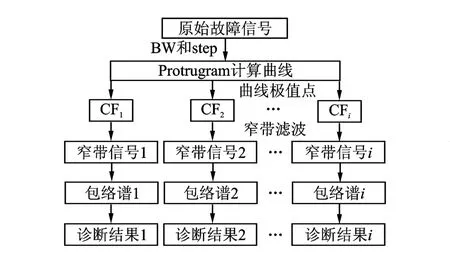
圖3　故障診斷流程圖Fig.3 Flow chart of fault diagnosis

3 仿真分析

采用仿真信號y（t）對多頻帶共振解調方法進行驗證，設置如下：采樣頻率25 k Hz，信號長度1 s，故障頻率125 Hz；添加3個沖擊共振頻率f1=4 k Hz，f2=7 k Hz，f3=10 k Hz；故障沖擊初始幅值分別為0.1，0.08，0.06；兩個干擾軸頻分別為f4=35 Hz，f5=11 Hz；幅值分別為1.0和0.8；干擾嚙頻為f6=455 Hz，幅值

0.3，仿真信號幅值為m V。y（t）表達式如式（2）所示。

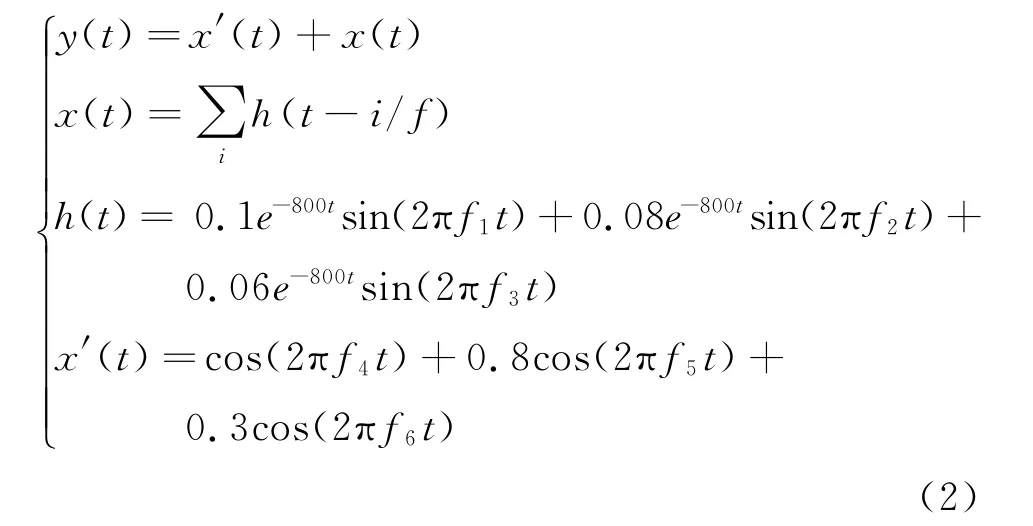
在仿真信號中添加高斯白噪聲n（t）以及沖擊干擾，這樣的干擾更加符合實際工況，分為兩種情況進行分析。第1種為低信噪比情況，n（t）的均方根為0.05，故障沖擊信號與噪聲n（t）的信噪比為-10.13 d B；第2種情況為高信噪比混有單一沖擊干擾，n（t）的均方根為0.005，故障沖擊信號與噪聲n（t）的信噪比為15.9 dB，混入沖擊信號的共振頻率為8 k Hz，初始幅值為1。兩種情況下的仿真信號及其各分量如圖4，5所示，為顯示效果清楚，圖4和圖5中僅畫出信號前0.08 s的波形。

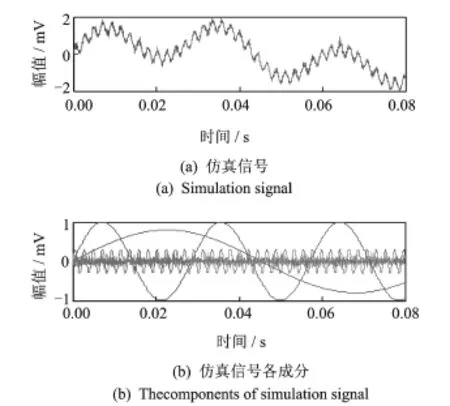
圖4　第1種情況仿真信號Fig.4 Simulation signal of first case

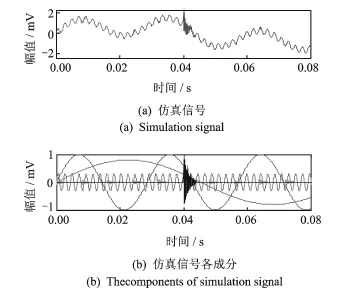
圖5　第2種情況仿真信號Fig.5 Simulation signal of second case

對兩種仿真信號用窄帶包絡解調方法尋找解調中心頻率，窄帶包絡解調時設置帶寬450 Hz（略大于3倍故障頻率），中心頻率迭代步長50 Hz。

第1種情況下，噪聲能量相對于故障能量強，故障信號信噪比低，Protrugram算法得到的中心頻率與窄帶濾波信號包絡譜峭度值的曲線如圖6所示。

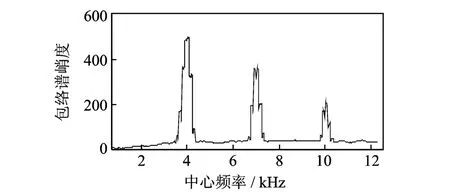
圖6　Protrugram算法結果曲線Fig.6 The result curve of Protrugram algorithm

從圖6中可以看到，窄帶包絡解調方法在4，7，10 k Hz附近均有局部極大值，并且峰值大小關系與仿真信號中故障沖擊初始幅值的大小關系一致，在3個峰值頻率處進行故障解調，得到3個包絡譜如圖7所示，從中均可以識別出清晰的故障頻率。由于濾波帶寬窄，包絡譜中高倍頻譜線衰減迅速，故障頻率譜線清晰明顯，易于識別。

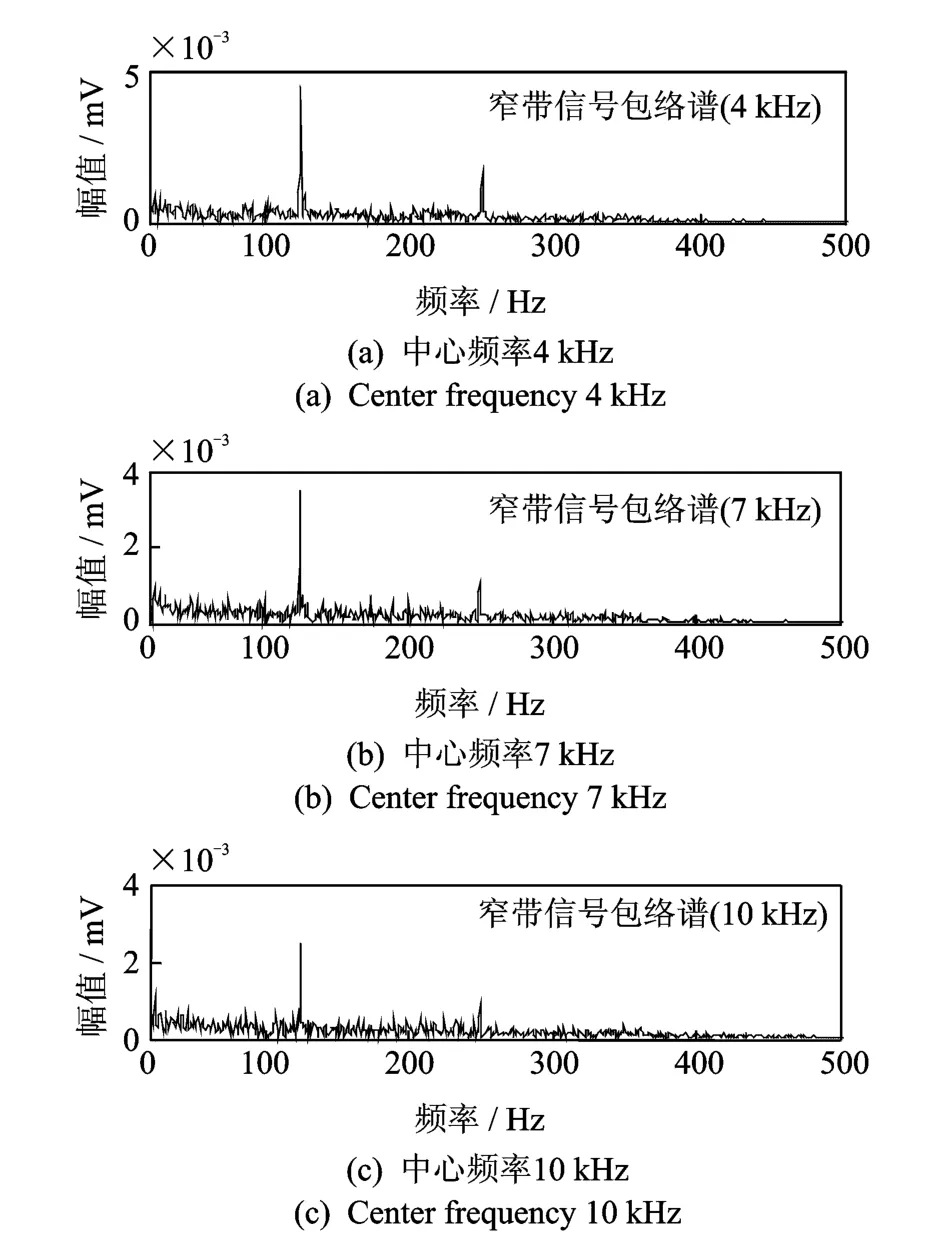
圖7　窄帶信號包絡譜Fig.7 Envelope spectrum of narrowband signal

第2種情況下，噪聲能量相對于故障能量較弱，故障信號信噪比較高，Protrugram算法得到的中心頻率與窄帶濾波信號包絡譜峭度值的曲線如圖8所示。

從圖8中可以看到窄帶包絡解調方法在4，7，10 k Hz附近均有局部極大值，對應著故障信號沖擊共振頻率，且故障信號初始幅值越大，對應包絡譜峭度值也越大。Protrugram算法得到的曲線在單一干擾的8 k Hz處沒有極值，說明窄帶包絡解調方法具有較強的抗沖擊干擾能力。在3個峰值頻率處進行故障解調，得到3個包絡譜如圖9所示，故障頻率譜線清晰，高倍頻衰減明顯，可以清楚地識別故障。

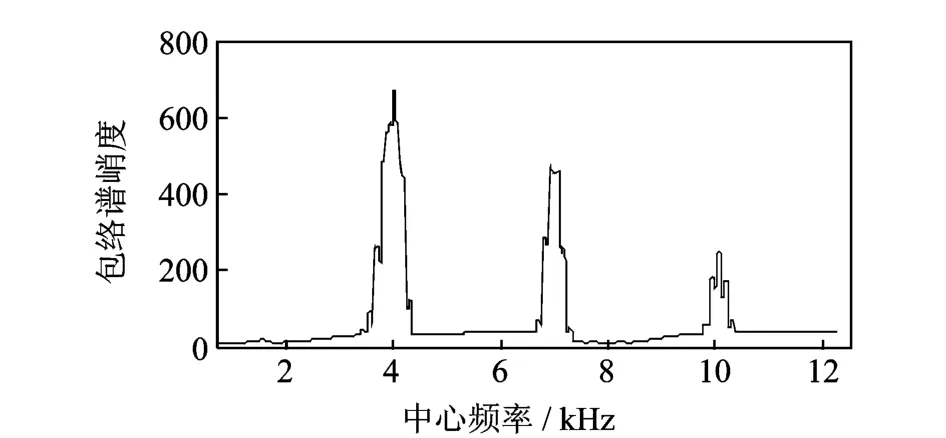
圖8　Protrugram算法結果曲線Fig.8 The result curve of Protrugram algorithm

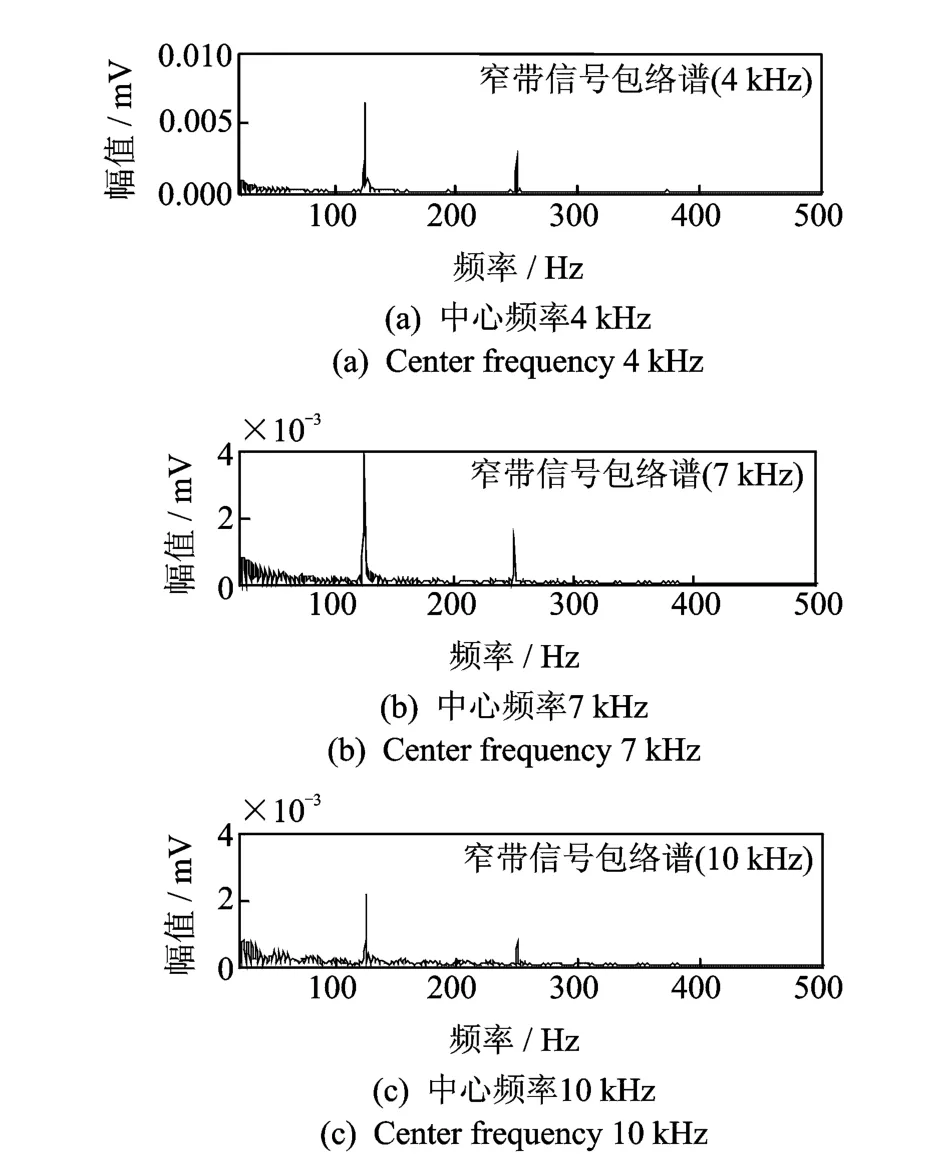
圖9　窄帶信號包絡譜Fig.9 Envelope spectrum of narrowband signal

4 試驗分析

利用試驗數據對窄帶包絡解調方法的多模態解調特性進行驗證，試驗齒輪箱結構及傳感器安裝如圖10所示。故障軸承安裝在齒輪箱中間傳動軸上，軸承型號6206，軸承參數：滾動體個數Z=9，滾動體直徑d=9.5 mm，軸承中徑D=46.5 mm，接觸角α=0。試驗中齒輪箱無負載運轉，聲發射傳感器為聲華R15型，全波形采集儀采樣頻率1 MHz。

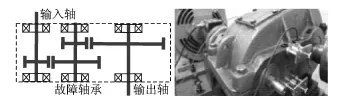
圖10　齒輪箱結構及傳感器布置Fig.10 Gearbox structure and sensor arrangement

4.1軸承外圈故障分析

試驗中軸承外圈預置故障為0.5 mm寬，1 mm深的線切割裂紋，齒輪箱輸入軸轉速1 488.92 r/ min，一級減速比為1∶2，根據外圈故障計算公式［12］得到故障頻率fouter=44.43 Hz，信號采集長度1 s，利用窄帶包絡解調Protrugram算法對故障信號進行處理，設定濾波帶寬150 Hz，迭代步長50 Hz，運算結果如圖11所示。

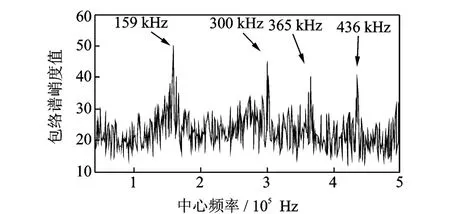
圖11　Protrugram算法結果曲線Fig.11 The result curve of Protrugram algorithm

圖11中曲線有4個明顯的局部尖峰極值，每個極值對應一個故障解調中心頻率，對4個極值頻率進行窄帶濾波并計算包絡譜，結果如圖12所示。從圖12的4張包絡譜中可以看到明顯的故障頻率譜線以及衰減后的二倍頻譜線，更高倍頻成分幾乎不可見，包絡譜中譜線數量少，故障頻率清晰，易于識別。

4.2軸承內圈故障分析

試驗中軸承內圈預置故障也是0.5 mm寬，1 mm深的線切割裂紋，齒輪箱輸入軸轉速610.18 r/ min，一級減速比為1∶2。根據內圈故障計算公式［12］得到故障頻率fouter=27.56 Hz，信號采集長度1 s，利用窄帶包絡解調Protrugram算法對故障信號進行處理，設定濾波帶寬100 Hz，迭代步長50 Hz，運算結果如圖13所示。

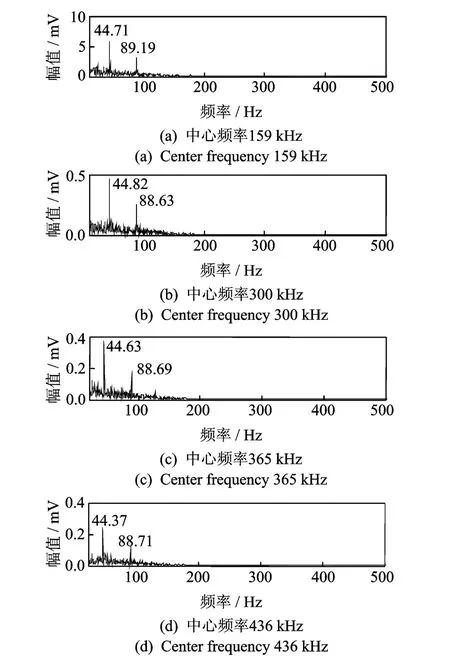
圖12　多頻帶解調包絡譜Fig.12 Multi-band demodulation envelope spectrum

內圈故障信號相對較弱，圖13中有兩個比較明顯的局部尖峰極值，對兩個極值對應的中心頻率進行窄帶濾波并計算包絡譜，結果見圖14。從圖14的兩張包絡譜中能看到明顯的故障頻率譜線及衰減后的二倍頻譜線，故障頻率可以清楚識別。

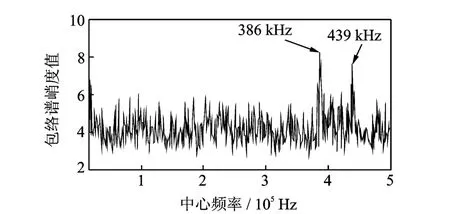
圖13　Protrugram算法結果曲線Fig.13 Tthe result curve of Protrugram algorithm

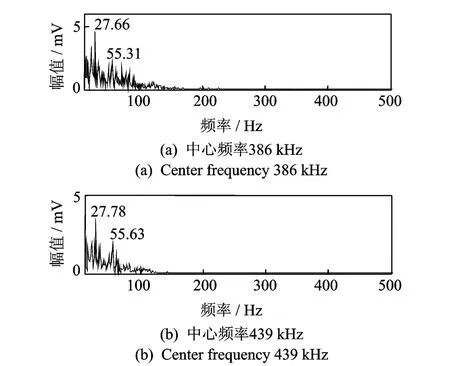
圖14　多頻帶解調包絡譜Fig.14 Multi-band demodulation envelope spectrum

4.3結果分析

由軸承內、外圈預置故障信號處理結果可知，在故障聲發射信號頻帶范圍內，能夠找到多個可用的故障頻率解調頻帶，外圈故障信號沖擊明顯，有4個較明顯的解調中心頻率，內圈故障沖擊相對微弱，有兩個較明顯的解調中心頻率。

軸承故障聲發射信號是一個復雜成分的寬頻帶信號，文中方法能搜索識別的中心頻率間隔理論最小值為濾波帶寬；當多個可用解調中心頻率的間距小于解調濾波帶寬時，文中方法無法將其區分，一般來講，間隔如此小的多個共振解調頻率完全可以作為一個解調窄帶來處理。

將窄帶解調方法的處理結果與寬帶濾波譜峭度方法處理結果進行對比，內、外圈故障的譜峭度方法處理結果如圖15所示。譜峭度方法在外圈故障處理中選擇的濾波中心頻率為250 k Hz，濾波帶寬166.7 k Hz，內圈故障處理中選擇的中心頻率為234.375 k Hz，濾波帶寬為31.25 k Hz。對比解調后的包絡譜可以發現，外圈故障能夠明顯識別，但濾波帶寬大，涵蓋了很多沖擊共振頻率，包絡譜中倍頻成分多且衰減緩慢，內圈故障濾波帶寬同樣較大，且由于故障沖擊微弱，寬帶濾波引入了較多背景干擾噪聲。因此解調包絡譜在故障頻率處峰值譜線受干擾嚴重，不夠明顯，故障特征頻率識別困難。與譜峭度方法相比，文中方法的優勢在于根據故障頻率選取濾波帶寬，找到多個可用的解調中心頻率，解調包絡譜中譜線數量有限，高倍頻衰減明顯，在干擾成分多的情況下能夠有效抑制噪聲的引入，有利于故障頻率譜線的識別。

5 結 論

1）軸承故障聲發射信號具有多頻帶共振解調特性，窄帶包絡解調Protrugram算法能夠搜索多個可用解調中心頻率，且各解調包絡譜中故障頻率譜線清晰，倍頻成分衰減明顯。

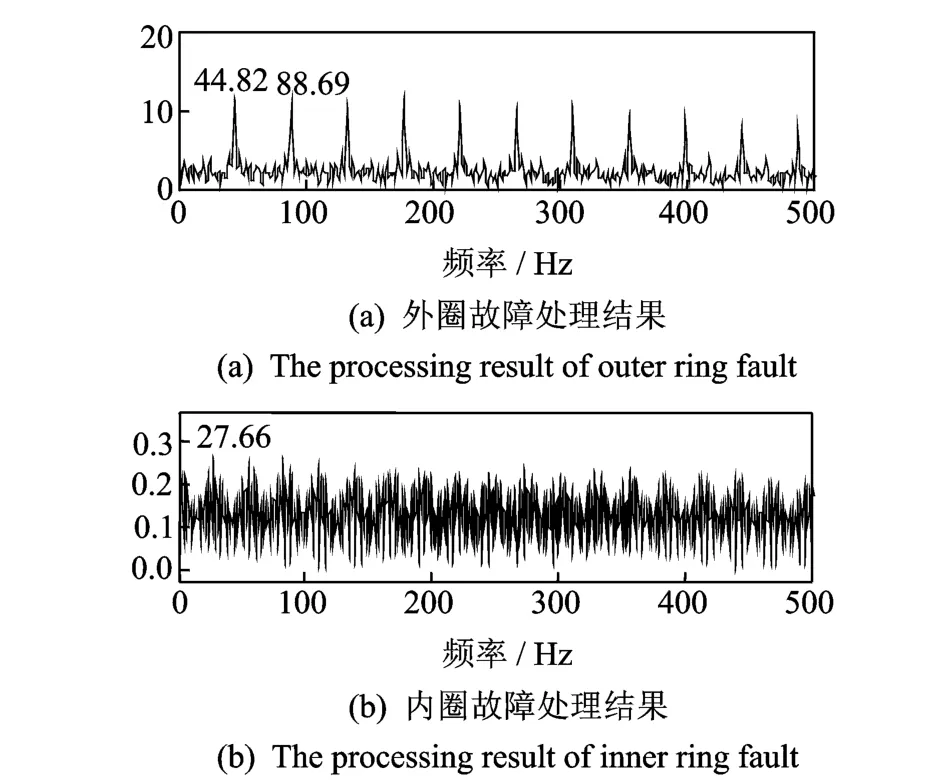
圖15　譜峭度方法包絡譜Fig.15 Envelope spectrum of spectral kurtosis method

2）內、外圈故障實驗信號處理結果表明，不同故障對應的多個解調中心頻率不完全相同，但解調中心頻率都處于聲發射信號的寬頻帶范圍內。

［1］ Gu Dongsik，Kim Jaegu，An Youngsu，et al.Detection of faults in gearboxes using acoustic emission signal［J］.Journal of Mechanical Science and Technology，2011，25（5）：1279-1286.

［2］ Mba D，Raj R B，Rao K N.Development of acoustic emission technology for condition monitoring and diagnosis of rotating machines；bearings，pumps，gearboxes，engines and rotating structures［J］.The Shock and Vibration Digest，2006，38（1）：3-16.

［3］ Eftekharnejad B，Carrasco M R，Charnley B，et al. The application of spectral kurtosis on Acoustic Emission and vibrations from a defective bearing［J］. Mechaniacl Systems and Signal Processing，2011，25（6）：266-284.

［4］ 焦敬品，何存富，吳斌.基于模態分析和小波變換的聲發射源定位新算法研究［J］.儀器儀表學報，2005，26（5）：482-485. Jiao Jingpin，He Cunfu，Wu Bin.A new acoustic emission source location technique based on wavelet transform and mode analysis［J］.Chinese Journal of Scientific Instrument，2005，26（5）：482-485.（in Chinese）

［5］ 鄧艾東，趙力，包永強.基于模糊熵的轉子碰摩聲發射信號的識別［J］.機械工程學報，2010，46（3）：71-75. Deng Aidong，Zhao Li，Bao Yongqiang.Recognition of rub-impact acoustic emission signal based on fuzzy entropy［J］.Journal of Mechanical Engineering，2010，46（3）：71-75.（in Chinese）

［6］ Gong Z，Nyborg E O，Oommen G.Acoustic emission monitoring of steel railroad bridges［J］.Materials E-valuation.1992，50（6）：883-887.

［7］ Chang Hong，Han Enhou，Wang Jianqiu.Analysis of modal acoustic emission signals of LY12CZ aluminum alloy at anodic and cathodic polarization［J］.NDT&E International，2006，39（7）：8-12.

［8］ Jiao Jingpin，He Cunfu，Wu Bin.Application of wavelet transform on modal acoustic emission source location in thin plates with one sensor［J］.International Journal of Pressure Vessels and Piping，2004，81（3）：427-431.

［9］ Ho D，Randall R B.Optimization of bearing diagnostics techniques using simulated and actual bearing fault signals［J］.Mechanical Systems and Signal Processing，2000，14（5）：763-788.

［10］Barszcz T，Jab″on′ski A.A novel method for the optimal band selection for vibration signal demodulation and comparison with the Kurtogram［J］.Mechanical Systems and Signal Processing，2011，25（6）：134-451.［11］Jab″on′ski A.Development of algorithms of generating an envelope spectrum of a vibration signal in the frequency domain for rolling element bearing fault detection［D］.Poland：Master Thesis AGH University of Science and Technology，2008.

［12］李輝，鄭海起，唐力偉.基于改進雙樹復小波變換的軸承多故障診斷［J］.振動、測試與診斷，2013，33（1）：53-59. Li Hui，Zheng Haiqi，Tang Liwei.Bearing multifaults diagnosis based on improved dual-tree complex wavelet transform［J］.Journal of Vibration，Measurement&Diagnosis，2013，33（1）：53-59.（in Chinese）

TN911.72；TH133.33

10.16450/j.cnki.issn.1004-6801.2015.02.000

張曉濤，男，1987年5月生，博士生。主要研究方向為機械系統性能檢測與故障診斷。曾發表《基于SVD與Fast Kurtogram算法的滾動軸承聲發射故障診斷》（《振動與沖擊》2014年第33卷第10期）等論文。

E-mail：headic@163.com

*國家自然科學基金資助項目（50775219）；軍隊科研資助項目［2011］（107）

2014-05-04；

2014-07-10