計入套圈變形和潤滑影響的球軸承動剛度研究

熊萬里　趙紫生　周　陽　呂　浪　侯志泉

1.湖南大學國家高效磨削工程技術研究中心,長沙,4100822.株洲聯誠集團有限責任公司湖南省軌道裝備冷卻工程中心,株洲,412001

計入套圈變形和潤滑影響的球軸承動剛度研究

熊萬里1趙紫生1周陽1呂浪1侯志泉2

1.湖南大學國家高效磨削工程技術研究中心,長沙,4100822.株洲聯誠集團有限責任公司湖南省軌道裝備冷卻工程中心,株洲,412001

針對傳統擬靜力學分析方法未考慮軸承套圈熱變形、離心力變形和彈流潤滑作用引起軸承內部溝道曲率中心與滾動體中心幾何位置關系的變化，難以準確反映軸承動剛度不足的現狀，建立了計入套圈變形和彈流潤滑影響的軸承擬靜力學修正模型。采用所建立的模型研究了軸承不同工作轉速和預緊力條件下軸承熱變形、離心力變形和潤滑油膜對動剛度的影響規律，通過與Gupta等典型算例及實驗的對比驗證，證實了所建立模型及分析結果的有效性。

角接觸球軸承；動剛度；套圈變形；彈流潤滑

0　引言

角接觸球軸承作為電主軸的核心支承部件，其動剛度直接影響電主軸的動態特性，主要特點在于:①高速旋轉內圈受離心力作用產生離心膨脹變形；②軸承摩擦發熱不可避免地使軸承套圈產生軸向、徑向熱膨脹變形;③彈流潤滑的膜厚分布影響滾動體與套圈溝道間的接觸變形。三者聯合作用使軸承內部曲率中心與滾動體中心的幾何位置關系發生改變，影響接觸角和接觸載荷的變化，增大軸承動剛度分析的難度。

國內外許多學者在Harris[1]提出的考慮鋼球受力與力矩不平衡的軸承動力學分析模型基礎上,對軸承剛度特性進行了大量深入的研究。羅祝三等[2]提出并推導了滾動軸承在任意方向支承剛度的數學表達式，探討了外載荷對軸承剛度的影響。Ali等[3]通過實驗研究了激振頻率、預緊力和轉速等參數對軸承動剛度的影響。Cao等[4]系統比較了不同預緊機制下，轉速對軸承剛度的影響，但忽略了軸承內部溫升和潤滑油膜的存在對剛度的影響，僅將接觸剛度進行合成近似代替軸承剛度。張峻暉等[5]探究了離心力和溫升對內圈和轉軸裝配過盈量的影響，但未研究離心力和溫升引起的套圈變形對軸承動剛度的影響。Lin等[6]提出了一個綜合電主軸動態、熱態性能模型,該模型定量研究了熱變形強化預緊力對剛度的影響,但未考慮轉軸和軸承座熱變形引起的套圈相對變形。現有研究中,軸承內部幾何關系分析尚不夠完善,計算模型考慮因素尚不全面,尤其沒有將彈流潤滑的影響考慮進模型，對高速主軸軸承在不同工況聯合套圈離心力和熱變形及潤滑特性的研究不夠深入。

本文建立了一個考慮因素較為全面的擬靜力學修正模型,揭示了在套圈離心力和熱變形及彈流油膜的影響下,軸承剛度隨預緊力和轉速的變化規律。

1　軸承套圈變形計算

1.1考慮離心效應的轉軸/內圈變形

軸承內圈隨轉軸旋轉產生的離心力在高速時不能忽略,并且它會導致軸承離心膨脹變形。根據彈性力學理論，將軸承內圈和與之配合的轉軸分別簡化為薄壁圓環和厚壁圓筒,推導出轉軸和內圈在配合處的離心膨脹變形計算式[7]:

(1)

(2)

式中,ucs為轉軸離心膨脹變形量;ρs、νs和Es分別為轉軸材料的密度、泊松比和彈性模量;ds為轉軸內徑;uci為內圈離心膨脹變形量；ρi、νi和Ei分別為內圈材料的密度、泊松比和彈性模量；ω為內圈角速度;d、di分別為內圈內徑和內圈溝道直徑。

由于內圈和轉軸常以過盈配合連接且二者相互約束,所以離心力作用下,內圈內徑和轉軸外徑的離心膨脹使配合表面過盈量減小。取轉軸和內圈的離心膨脹引起的過盈量為

Ic=uci-ucs

(3)

由于離心力變形與轉速的平方成正比,轉速提高,轉軸與內圈在配合表面處內圈的離心膨脹變形量較轉軸的離心膨脹變形量大，因此，轉軸離心膨脹變形不會影響軸承內部徑向間隙的變化，考慮內圈和轉軸離心膨脹變形對軸承內部幾何關系的影響時只需計入內圈離心膨脹變形即可。

1.2套圈熱膨脹變形

電主軸高速旋轉時，電機損耗發熱和軸承摩擦發熱使得主軸和軸承溫度升高，并通過熱傳導和熱輻射使軸承零件溫度上升，所以內外套圈間產生軸向、徑向相對熱變形。通常，軸承薄壁圓環零件熱變形采用Harris給出的計算方法：

u=adTΔT

(4)

式中,u為熱變形;a為熱膨脹系數;ΔT為溫升;dT為零件直徑。

考慮到溫度分布的軸對稱性,長圓柱為平面應變，應變由熱變形和熱應力共同引起,根據彈性理論應力-應變關系得到外徑R任意位置r處實心圓柱的徑向熱變形方程[8]:

(5)

式中，ν為泊松比。

由式(4)得內圈溝道直徑和內徑在溫升ΔTi時的熱變形量分別為

(6)

由式(5)得轉軸外徑在溫升ΔTs時的熱變形量為

us=asΔTs(1+νs)d

(7)

溫升引起的轉軸-內圈配合過盈量的變化值為

ITi=u″i-us=[aiΔTi-asΔTs(1+νs)]d

(8)

綜合式(6)～式(7)得考慮轉軸熱變形時的內圈溝道徑向熱變形：

aiΔTidi+[asΔTs(1+νs)-aiΔTi]d2/di

(9)

式中,ai、as分別為內圈和轉軸的熱膨脹系數。

同理得考慮軸承座熱變形影響的外圈溝道徑向熱變形量為

(10)

式中,ah、νh分別為軸承座的熱膨脹系數和泊松比;D、De分別為外圈外徑和外圈溝道直徑；ΔTh為軸承座溫升。

滾動體在溫升為ΔTb時的熱變形量為

ub=abΔTbDb

(11)

式中,ab為滾動體的熱膨脹系數;Db為球徑。

溫升引起的外圈-軸承座配合過盈量的變化值為

ITe=[aeΔTe-ahΔTh(1+νh)]D

(12)

式中,ae為外圈熱膨脹系數;ΔTe為外圈溫升。

綜合式(9)～式(11)得套圈溝道間徑向相對熱變形量如下：

ur=ui-ue-2ub

(13)

軸承雙聯配置下,套圈溝道間軸向相對熱變形量為

ua=±(ahΔThLh-asΔTsLs)/2

(14)

其中,正號用于雙“O”配置,負號用于雙“X”配置;Ls、Lh分別為轉軸和軸承座的有效長度。

2　軸承彈流潤滑油膜的影響及計算

2.1彈流潤滑最小油膜厚度

潤滑是保證軸承高速性的一個重要條件,它能夠使得滾動體與套圈溝道間保持一定厚度的潤滑油膜。根據彈性流體潤滑理論，潤滑油膜的油膜剛度由最小油膜厚度決定。在等溫且供油充分的條件下，滾動體與套圈溝道間量綱一中心油膜厚度H0和最小油膜厚度Hmin為[9]

(15)

式中,U為量綱一速度參數；G為量綱一材料參數；W為量綱一負荷參數；k為橢圓率。

滾動體與套圈溝道間中心油膜厚度h0和最小油膜厚度hmin定義為

(16)

式中,Rx為滾動體沿運動方向的當量曲率半徑。

彈性流體潤滑(EHL)理論與非線性赫茲接觸(Hertz)理論的區別在于是否考慮潤滑油膜的存在，EHL和Hertz接觸狀態下膜厚分布及壓力分布如圖1所示。

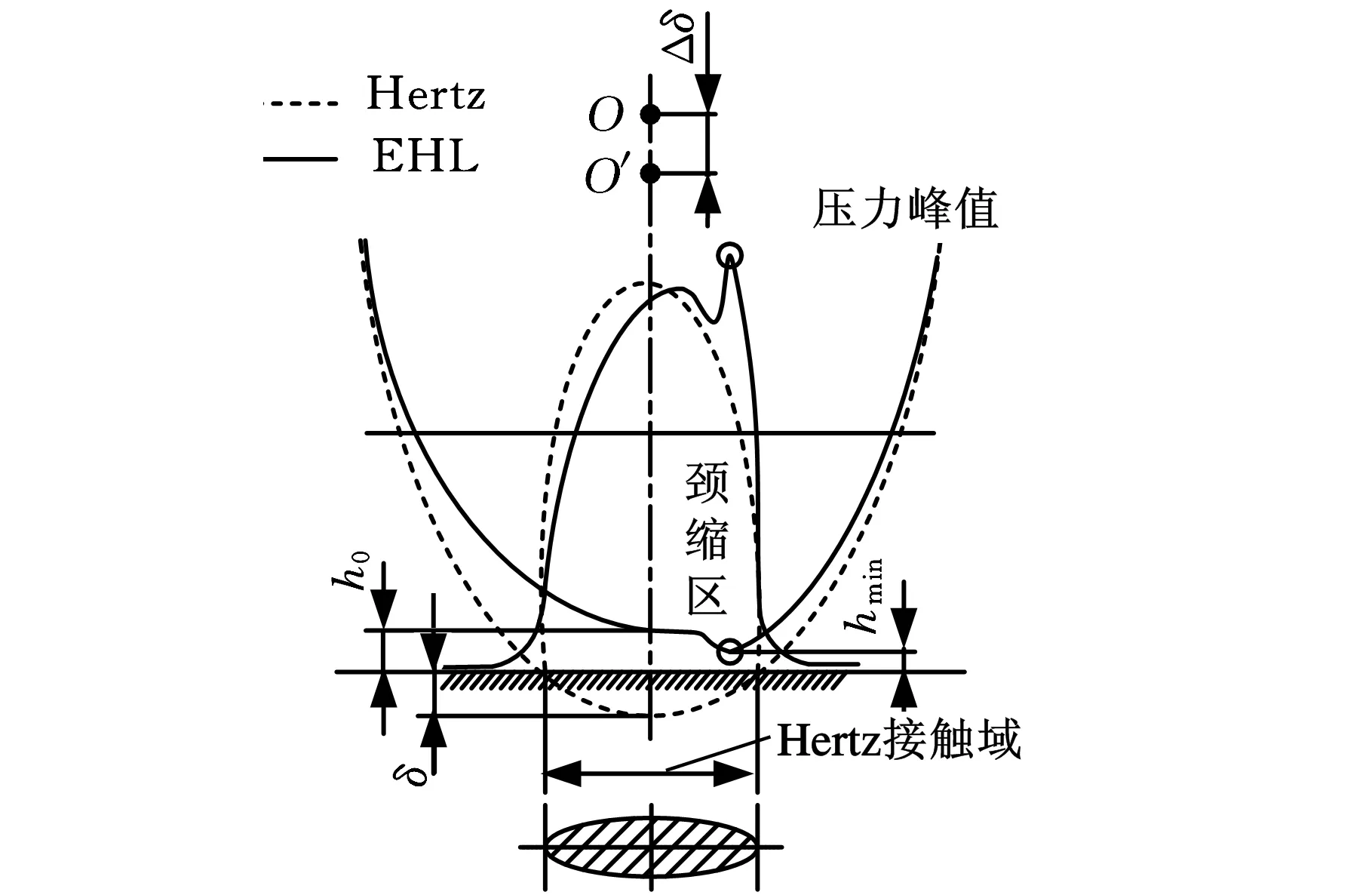
圖1　Hertz及EHL接觸狀態下膜厚和壓力分布

潤滑油膜的存在使滾動體與套圈溝道間的彈性變形減小，計算實際接觸剛度時，滾動體與套圈溝道間徑向彈性變形量應是考慮油膜厚度后的徑向趨近量：

Δδ=δ-h0

(17)

式中,Δδ為EHL狀態下彈性變形量；δ為Hertz接觸點處的彈性變形量；h0為EHL接觸點處的中心油膜厚度。

2.2油膜剛度的計算

滾動體與套圈溝道間接觸載荷Q和最小油膜厚度hmin之間的關系可由式(16)推導得出，即

(18)

式中,E′為接觸體的等效彈性模量;ν1、ν2和E1、E2分別為兩接觸體的泊松比和彈性模量。

根據剛度定義,油膜剛度Koil為

(19)

對于高速、超高速角接觸球軸承，滾動體與內外圈接觸角不等，造成對應接觸載荷的大小、方向不同，使得內外圈接觸剛度也不同，實際中，軸承內外剛度應由滾動體與套圈溝道間的接觸剛度和油膜剛度共同組成：

(20)

式中,Kj為滾動體j與套圈的等效內外剛度;Kc,j為滾動體j與套圈的接觸剛度;Koil,j為滾動體j與套圈的油膜剛度。

3　角接觸球軸承擬靜力學修正模型

3.1基本方程

為了便于分析,對計算模型進行相應的簡化:①忽略球位置的影響，假設每個球受力和相對位移相同；②忽略轉軸與內圈以及外圈與軸承座表面粗糙度引起的過盈量對軸承套圈溝道曲率中心相對位置的影響；③忽略溫升對潤滑介質性能的影響；④忽略保持架對滾動體力與運動的影響。

3.1.1滾動體運動分析

電主軸角接觸球軸承為外圈固定，內圈旋轉，假定內圈以角速度ω勻速穩定旋轉，考慮到滾動體與套圈溝道有相對滑動，則引入套圈控制理論，采用Jones給出的控制類型條件。若滿足不等式：

QejαejΣej(e)cos(αij-αej)>QijαijΣij(e)

(21)

式中,Qij和Qej分別為滾動體j與內外圈的接觸載荷;αij和αej分別為滾動體j與內外圈的接觸角;Σij(e)和Σej(e)分別為滾動體j與內外圈接觸處的第二類完全橢圓積分。

則為外圈控制,此時滾動體j的公轉、自轉角速度與內圈角速度的比值分別為

(22)

式中，γ′為球徑與軸承中徑的比值。

若滿足不等式：

QijαijΣij(e)cos(αij-αej)>QejαejΣej(e)

(23)

則為內圈控制,此時滾動體j的公轉、自轉角速度與內圈角速度的比值分別為

(24)

3.1.2位移協調方程

由于外圈與軸承座固定，故外圈曲率中心不變。動力學特性分析中，在徑向力Fr、軸向力Fa和力矩M聯合作用下，軸承內外圈產生相對徑向、軸向、角向位移δr、δa和θ。如圖2所示，給出內外圈溝道曲率中心與角位置ψj處滾動體中心之間的幾何位置關系。

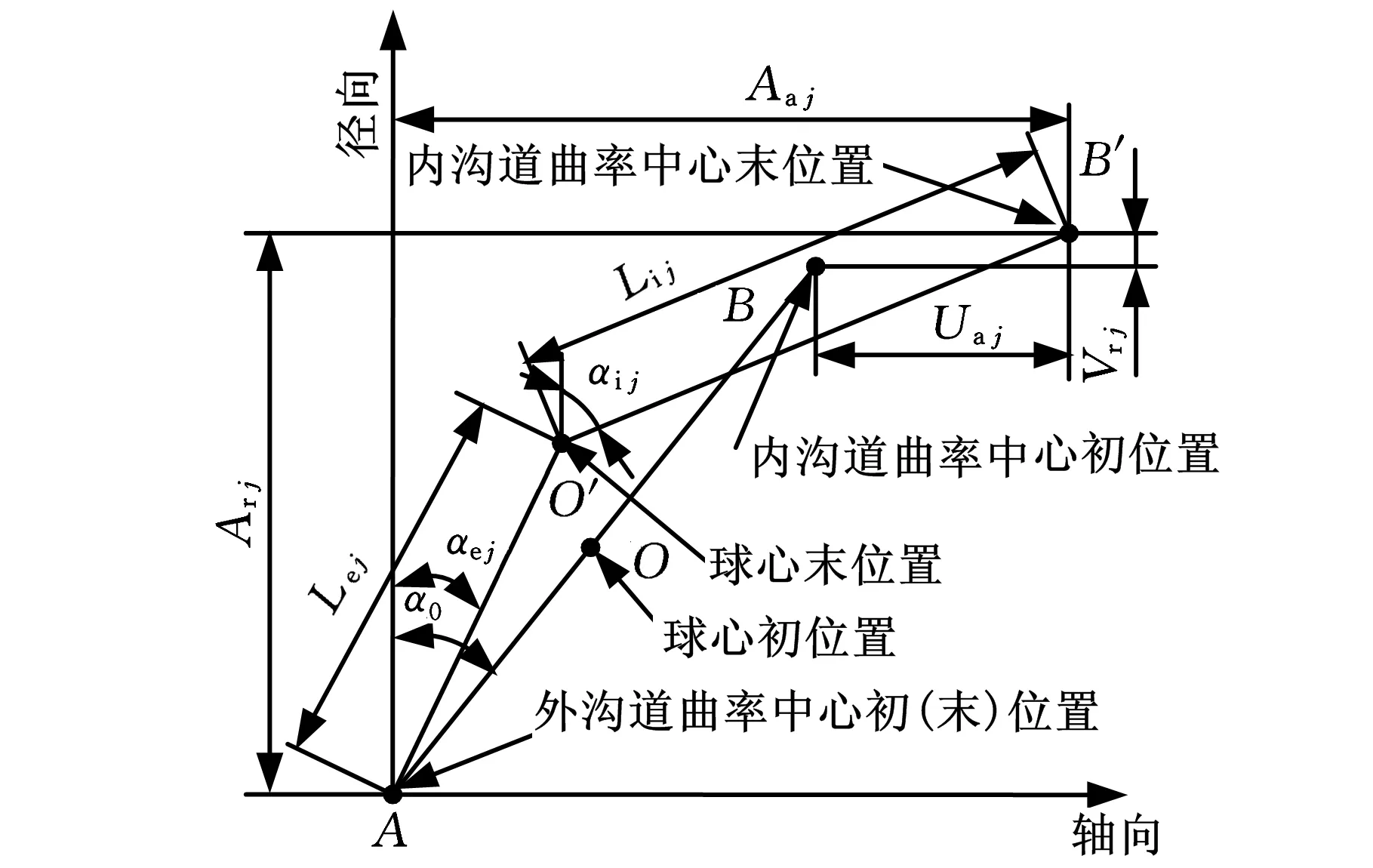
圖2　球心與內外溝道曲率中心的相對位置

無載荷時，內外溝道曲率中心間的距離為

dAB=(fi+fe-1)Db

式中,fi和fe分別為內外溝道曲率半徑系數。

任意球位置處,對于滾動體j有

Aaj=dABsinα0+UajArj=dABcosα0+Vrj

式中,α0為初始接觸角;Aaj、Arj分別為內外溝道曲率中心末位置之間的軸向和徑向距離;Ua j、Vr j分別為內溝道曲率中心初、末位置的軸向和徑向距離。

由圖2,根據曲率中心相對位置，可得滾動體中心位置變化的位移協調方程：

(25)

式中,Lij、Lej分別為球心末位置與內外溝道曲率中心末位置的距離。

如前文所述，潤滑油膜直接作用于滾動體與套圈的接觸變形；離心力變形和套圈溝道間徑向熱變形最終表現為內圈徑向溝道變形，套圈溝道間軸向熱變形直接作用于軸向溝道變形。即套圈變形和潤滑油膜改變球心末位置與內外溝道曲率中心末位置的距離及內溝道曲率中心初末位置的軸向和徑向距離，改變Uaj、Vrj、Lij和Lej的大小，給出角接觸球軸承擬靜力學修正模型如下。

考慮綜合套圈離心變形和熱變形的修正模型如下：

Uaj=δa+θRicosψj+ua

Vrj=δrcosψj+uci+ur

Lij=(fi-0.5)Db+δij

Lej=(fe-0.5)Db+δej

式中,Ri為內圈溝道曲率中心所在的圓周半徑;uci為內圈離心力變形量；ua、ur分別為套圈溝道間的軸向和徑向熱變形量;δij、δej分別為滾動體j和內外圈接觸點處的Hertz彈性變形量。

計入彈流潤滑考慮綜合套圈變形的修正模型如下：

Uaj=δa+θRicosψj+ua

Vrj=δrcosψj+uci+ur

Lij=(fi-0.5)Db+δij-hij

Lej=(fe-0.5)Db+δej-hej

式中,hij、hej分別為滾動體j和內外圈接觸點處的油膜厚度。

3.1.3球滾動體和內圈受力平衡方程

軸承高速旋轉，滾動體受離心力、摩擦力、陀螺力矩和套圈對其接觸力共同作用，滾動體和內圈受力如圖3所示。

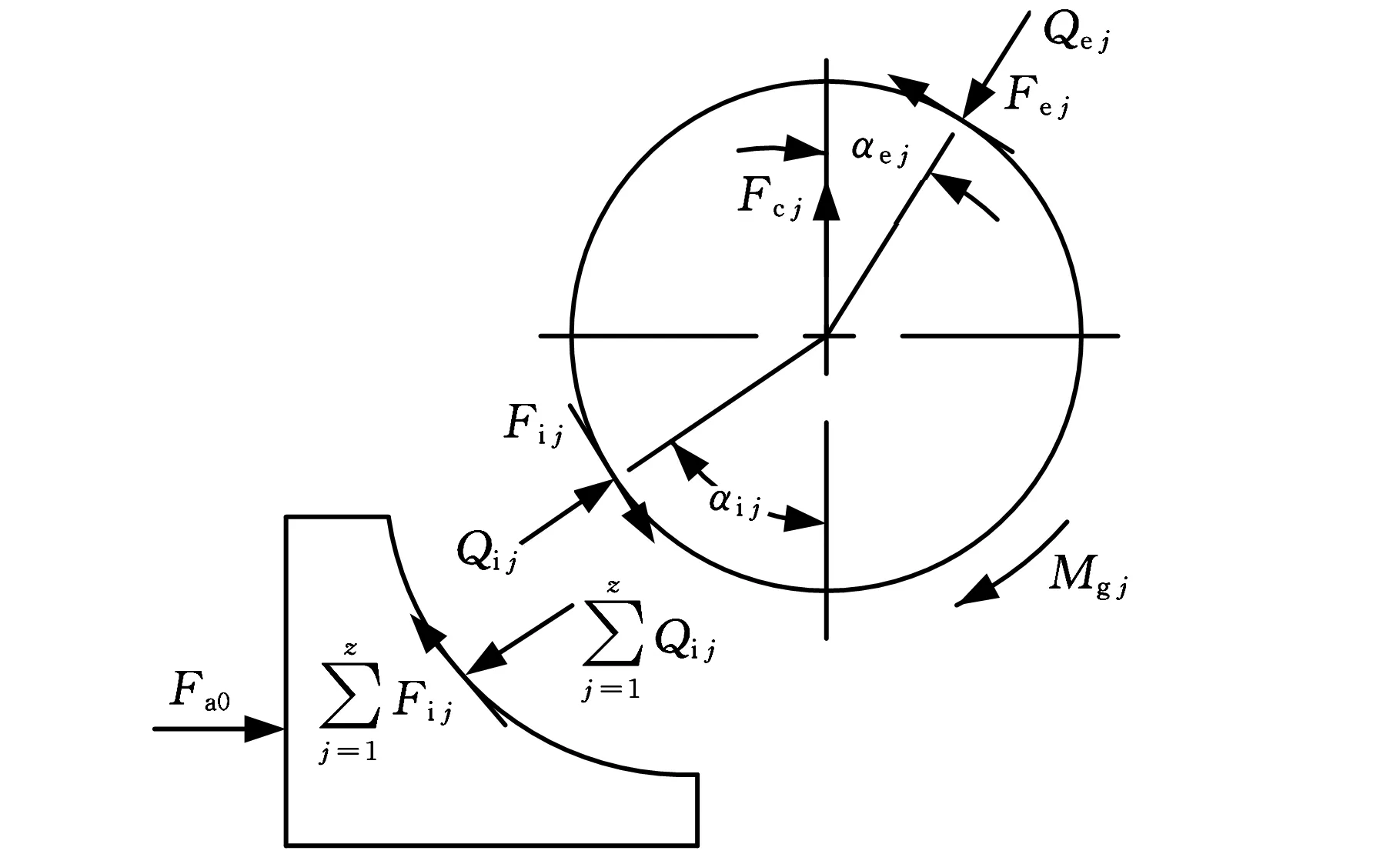
圖3　滾動體與內圈受載圖

對每個滾動體受力均可建立受力平衡方程：

(26)

式中,Kij、Kej分別為滾動體j與內外圈的接觸剛度；Fcj為滾動體j的離心力;Fij、Fej分別為滾動體j與內外圈的接觸摩擦力，與滾動體的陀螺力矩有關。

作用于整個軸承的負荷應該平衡，即內圈所受合力為零，根據內圈水平和垂直方向受力平衡，以及力矩平衡條件，則有

(27)

式中,z為滾動體數目;Fa0為初始預緊力;ri為內圈溝道曲率半徑,ri=fiDb。

3.2基本方程組求解步驟

基于綜合套圈變形及彈流潤滑油膜影響的修正模型，利用仿真軟件MATLAB對軸承進行動力學數值仿真，求解得到軸承相關動態特性參數及動剛度，具體數值算法如下。

(1)根據軸承基本參數，設定初始接觸角α0，利用Newton-Raphson法迭代求解靜力學非線性方程，得到滿足精度的接觸角和初始軸向位移。

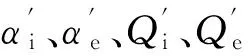
(3)根據式(27),調整δa、δr和θ的值，重復步驟(2)，直到δa、δr、θ滿足預先設定的精度。以迭代變量αi、αe、Qi、Qe為基礎計算軸承動態特性參數，利用文獻[10]中剛度的計算方法得到軸承的徑向剛度Kr、軸向剛度Ka和角剛度Kan。

(4)在傳統分析模型的基礎上，將轉軸、軸承、軸承座作為一個系統，采用節點網絡法[11],結合軸承運動學及主軸系統溫度場模型，計算主軸系統轉軸、軸承零件、軸承座的溫度，由式(13)～式(14)分別計算出套圈軸向、徑向熱變形；計算內圈離心力變形和內外圈油膜厚度。

(5)將套圈變形和彈流油膜的計算結果分別導入位移協調方程(式(25)),修正軸承內部幾何關系和軸承工況，對修正模型進行反饋迭代，直至滿足預設精度，計算修正模型的軸承動態特性參數及動剛度。

3.3傳統分析模型的算例驗證

采用軸承動力學計算的典型算例[12]和文獻[13]算例進行驗證。該算例可計算軸承的接觸角、接觸載荷、旋滾比，但未考慮套圈離心力和熱變形及彈流潤滑的影響。在未考慮上述因素的情況下，使用本文基于傳統分析模型編寫的程序進行仿真計算，并與Gupta[12]的TABACY程序和文獻[13]程序計算結果進行比較，從而間接驗證本文考慮套圈變形及彈流潤滑影響的修正模型數值仿真的正確性。

文獻[12]算例中軸承基本參數為:球個數19，球徑15.081 mm,節圓直徑105 mm，接觸角25°,溝曲率系數0.52，軸承零件彈性模量206 GPa,泊松比0.3;初始預緊力889.84 N,工作轉速15 000 r/min。計算結果如表1所示。

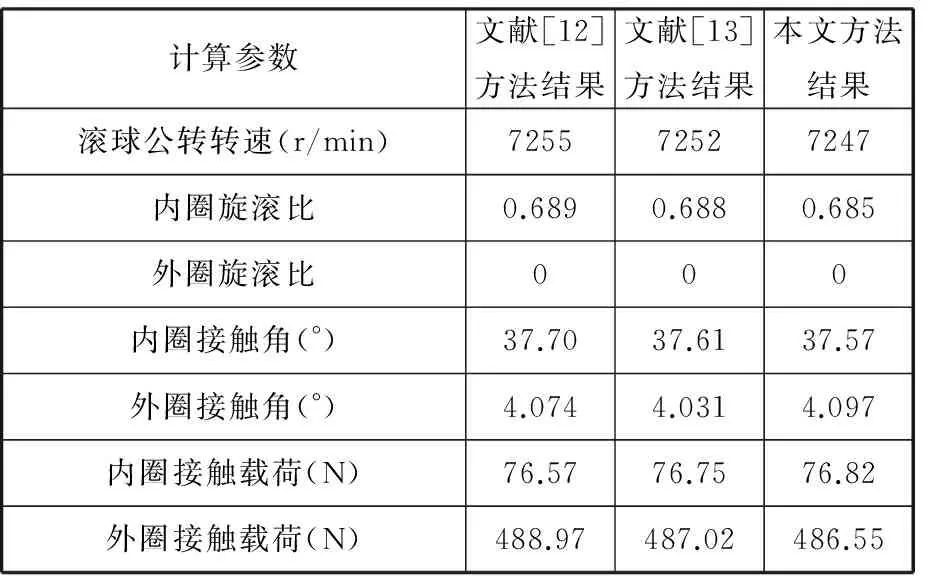
表1　計算結果比較

對比計算結果可知,本文計算結果與文獻[12-13]結果匹配性較好，仿真值與文獻[13]實驗結果基本一致。由于本文模型以接觸角、接觸載荷為迭代變量,從而驗證了本文傳統分析模型對軸承動態特性參數和動剛度仿真的精度，進一步驗證了基于傳統分析模型所建立的修正模型的可靠性。

3.4動剛度規律研究

本文以湖南大學研制的35 kW/18 000 r·min-1加工中心電主軸為例,研究串聯雙“O”型配置單個角接觸球軸承7013CD/HCP4在定壓預緊機制，不同工況下套圈變形和彈流潤滑對軸承動剛度的影響規律。軸承參數為:內徑65 mm，外徑100 mm，寬度18 mm,球徑11.11 mm，球數20,初始接觸角15°，溝曲率系數0.54、0.57,滾動體材料為氮化硅，套圈材料為軸承鋼。潤滑采用10號主軸油，油氣潤滑方式，工作環境溫度為25 ℃。潤滑油特性為[14]:動力黏度η0=0.027 Pa·s,黏壓系數α=2.3×10-8Pa-1。裝配過盈配合量約20 μm。

需要提出的是,離心力使得轉軸與內圈裝配過盈量減小，轉軸、軸承零件和軸承座溫升使得轉軸與內圈裝配過盈量增大，綜合考慮離心力和溫升對裝配過盈量的影響會相互抵消一部分[5],在本例中綜合離心力和溫升引起的過盈量對軸承動態特性參數影響不大。

3.4.1套圈離心和熱變形分析

圖4所示為預緊力為300 N時套圈離心力變形和熱變形隨轉速的變化情況。套圈離心力變形量和熱變形量隨轉速的升高而增大。轉速為24 kr/min時,內圈和轉軸在離心力作用下離心變形量分別為9.34 μm、2.87 μm；內外圈在熱效應下產生的軸向、徑向熱變形量分別為1.58 μm、5.03 μm;由離心力引起的內圈和轉軸有效配合過盈量為6.47 μm。考慮軸承座和轉軸熱變形的影響，套圈徑向熱變形較軸向大。

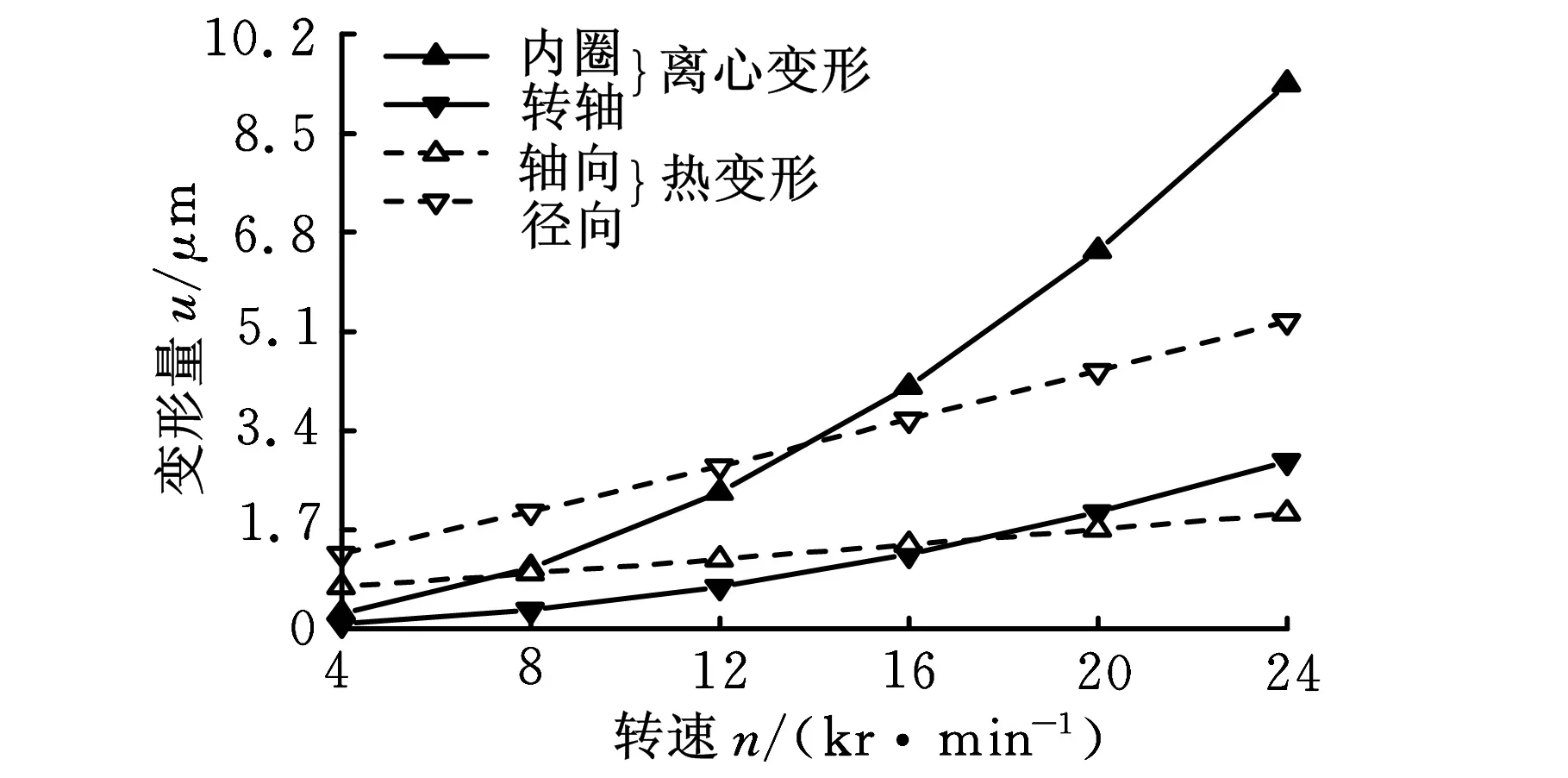
圖4　套圈離心變形和熱變形與轉速的關系

圖5所示為主軸轉速為20 kr/min時套圈變形隨軸向預緊力的變化情況。轉速恒定，轉軸和內圈離心變形恒定不變，分別為1.99 μm、6.49 μm。套圈間徑向、軸向熱變形隨預緊力的增大而增大，這是由于預緊力增大強化接觸載荷，導致軸承零件溫升加劇，熱變形增加。

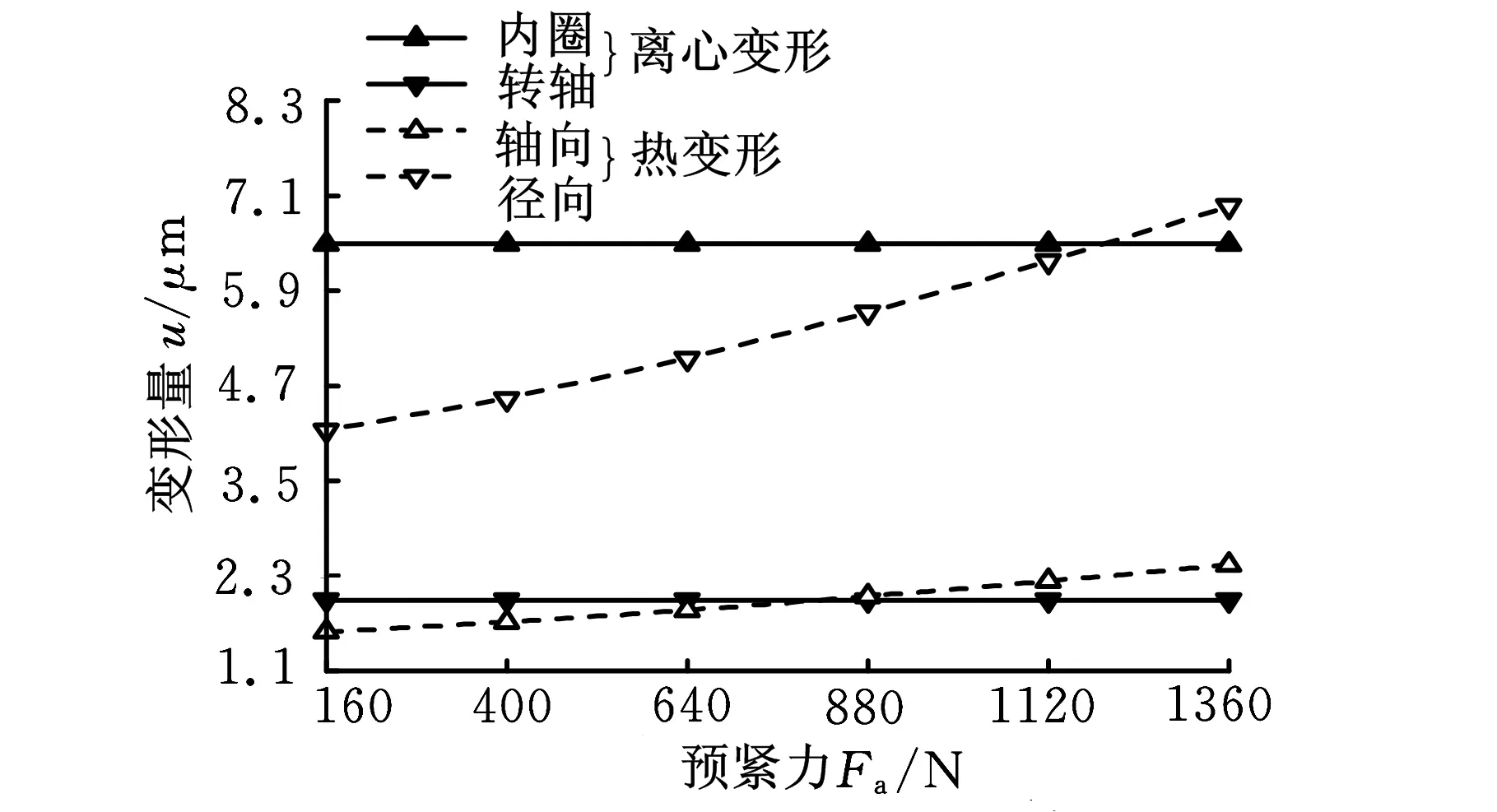
圖5　套圈離心變形和熱變形與預緊力的關系

3.4.2彈流油膜厚度和剛度分析

圖6所示為預緊力為300 N時滾動體與套圈間最小油膜厚度和剛度隨轉速的變化情況。轉速增大使滾動體與套圈間的潤滑油流速加快,膜厚增加；內圈油膜剛度減小；外圈油膜剛度先減小后增大,且外圈油膜剛度較內圈大。這是由于轉速增大后,滾動體離心效應增強,與外圈接觸載荷迅速增大，與內圈接觸載荷減小。

圖6　最小油膜厚度和油膜剛度與轉速的關系

圖7所示為轉速為20 kr/min時滾動體與套圈間最小油膜厚度和剛度隨預緊力的變化情況。預緊力增大,最小油膜厚度減小，油膜剛度增大。同一預緊力下，外圈油膜剛度較內圈油膜剛度大,這是由于轉速較高，外圈接觸載荷大于內圈接觸載荷,單一改變預緊力,只是不同程度上增大接觸載荷,但并不改變接觸載荷的大小分布。

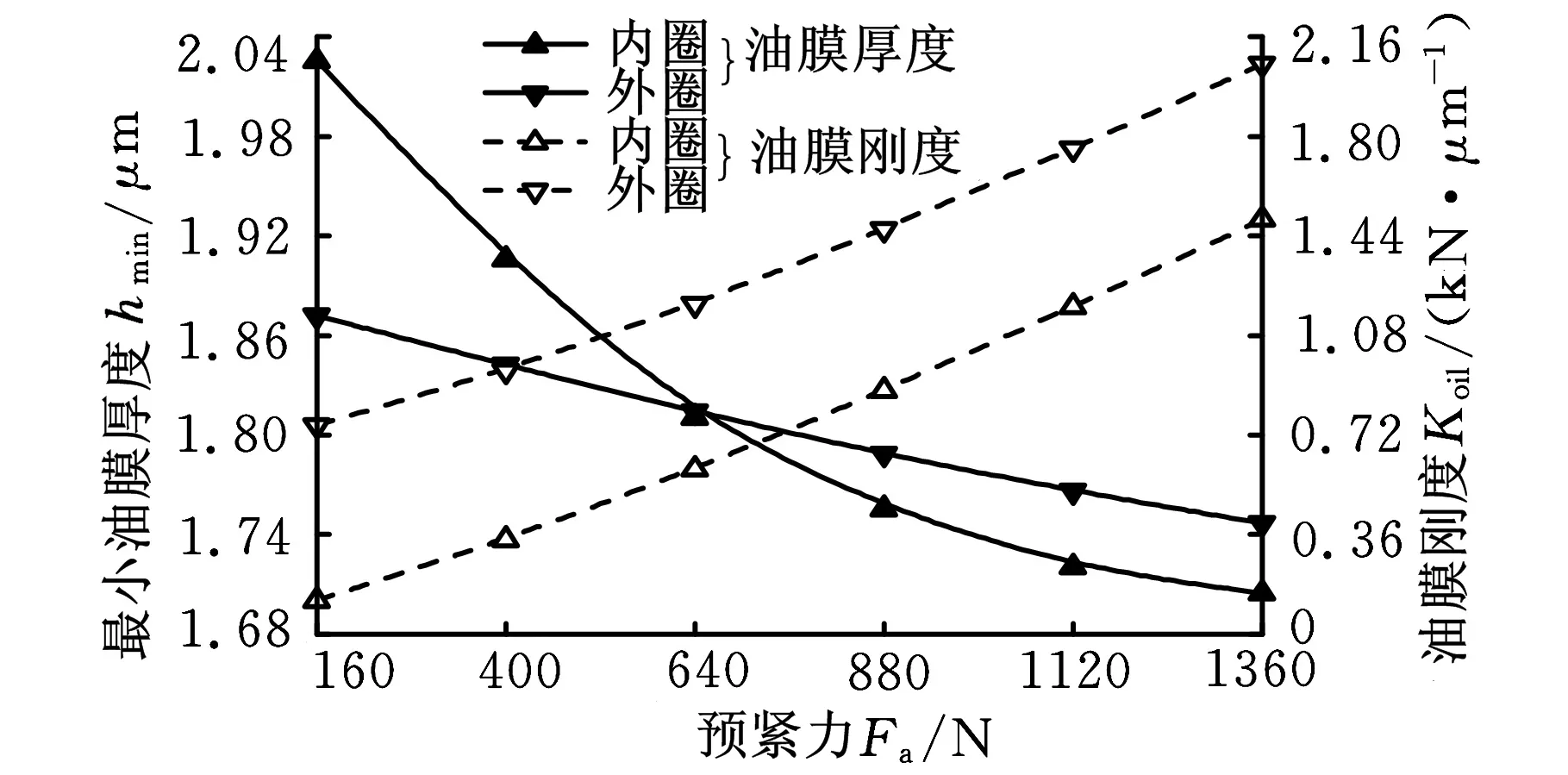
圖7　最小油膜厚度和油膜剛度與預緊力的關系

3.4.3綜合套圈離心和熱變形對動剛度的影響

軸承動剛度在不考慮彈流潤滑時計算結果如圖8、圖9所示。圖8所示為300 N預緊力時，綜合套圈變形對軸承動剛度的影響。隨著轉速的增大,軸承徑向、軸向和角向剛度呈非線性減小，其剛度變化是由于定壓預緊下，轉速升高，內圈與滾動體接觸角逐漸增大，且變化幅度較大，從而減小了徑向剛度；外圈與滾動體的接觸角減小使得軸向剛度和角剛度顯著降低。綜合套圈變形在一定程度上提高了徑向剛度(圖8a)，且轉速越大，套圈變形對徑向剛度的影響越明顯。綜合套圈變形對軸承軸向和角剛度的影響幅度很小，可忽略不計(圖8b、圖8c)。

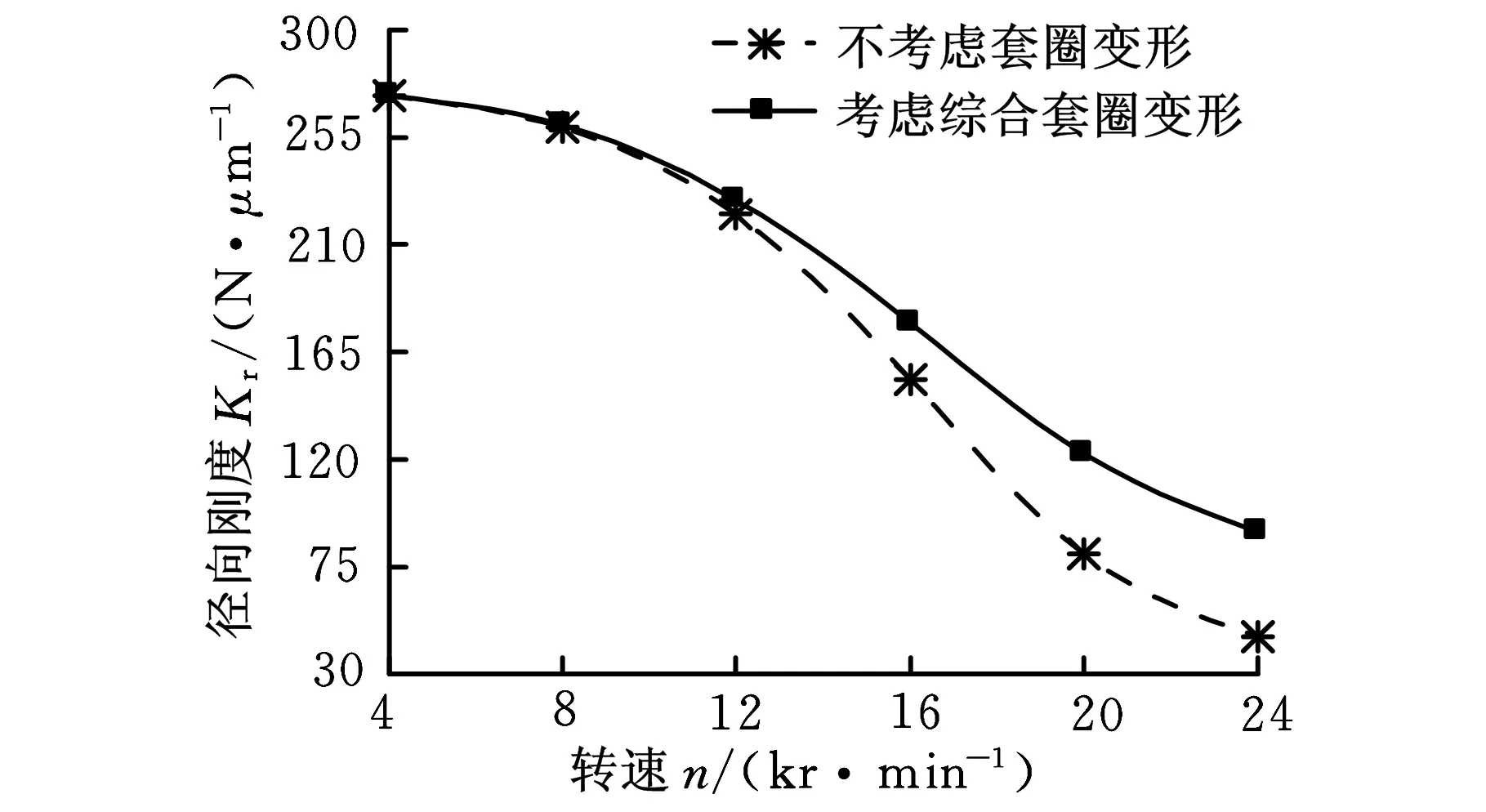
(a)徑向剛度

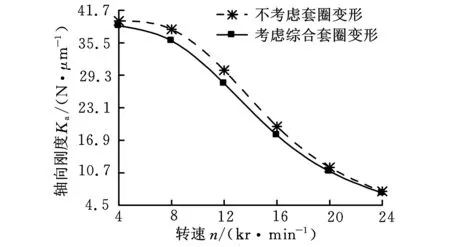
(b)軸向剛度

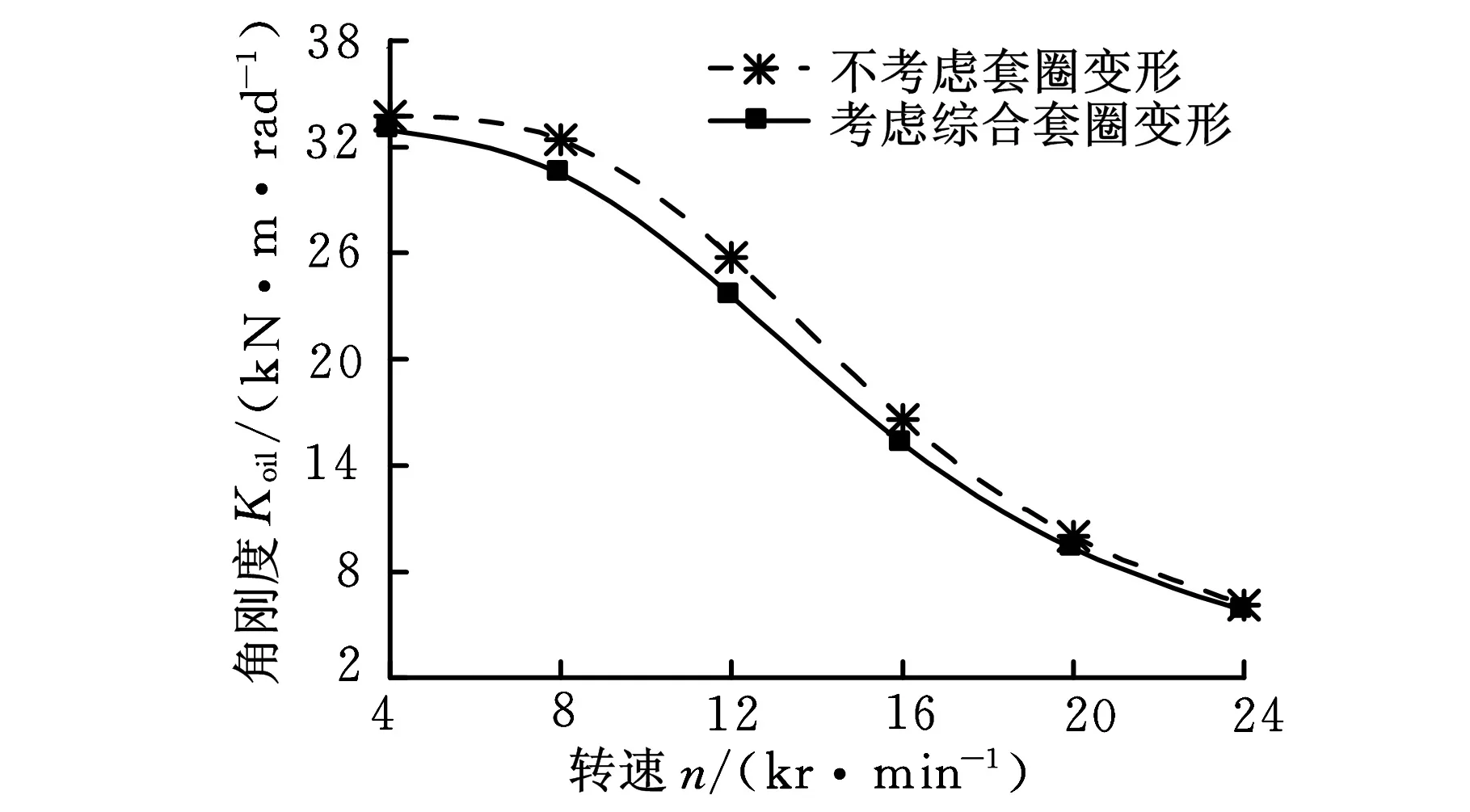
(c)角剛度圖8　不同轉速下軸承的動剛度

圖9所示為轉速為20 kr/min,套圈變形對軸承動剛度的影響。軸承徑向、軸向和角剛度隨預緊力的增大而增大。轉速一定，預緊力增大使滾動體與套圈間的接觸載荷增加,內外圈法向接觸剛度變大，串聯作用下使軸承徑向、軸向和角剛度增加，這與文獻[15]的分析結果一致。綜合套圈變形使得軸承徑向剛度增大(圖9a)，軸向剛度和角剛度減小(圖9b、圖9c)，且預緊力越大，套圈變形對軸向剛度和角剛度影響越明顯。這是因為考慮套圈變形時，內圈受離心力影響，滾動體與內圈接觸角減小，接觸載荷增大;這與未考慮綜合套圈變形時，內圈與滾動體接觸角增大,接觸載荷減小的變化趨勢相反。在外圈接觸剛度保持不變的情況下，內圈離心變形使內圈接觸剛度和徑向剛度增大。套圈變形對外圈接觸角和接觸載荷影響較小，但在預緊力的作用下，外圈接觸角減小使軸向剛度和角剛度減小。

(a)徑向剛度

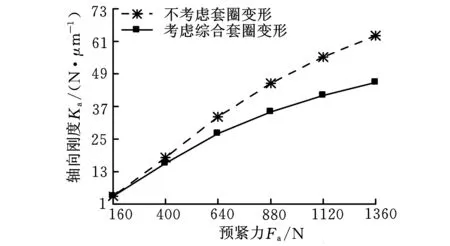
(b)軸向剛度

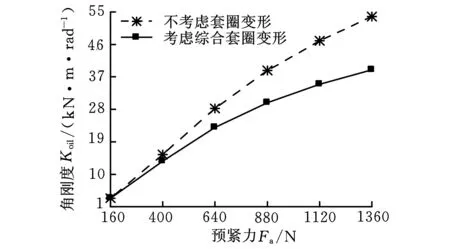
(c)角剛度圖9　不同預緊力下軸承的動剛度

3.4.4彈流油膜對動剛度的影響

圖10～圖12為計入彈流潤滑考慮綜合套圈離心和熱變形時，軸承分別在中預緊(320 N)和大預緊(640 N)下潤滑油膜對動剛度的影響。圖10中，同一速度參數條件下，對于不同預緊力，考慮彈流油膜，軸承徑向剛度均有不同程度的減小(軟化)，且轉速越大，彈流油膜對徑向剛度的影響越顯著。這是由于套圈變形強化軸承接觸剛度，使得接觸剛度和油膜剛度量級相差不多，且油膜剛度較接觸剛度大，并聯作用下使得軸承總剛度下降。

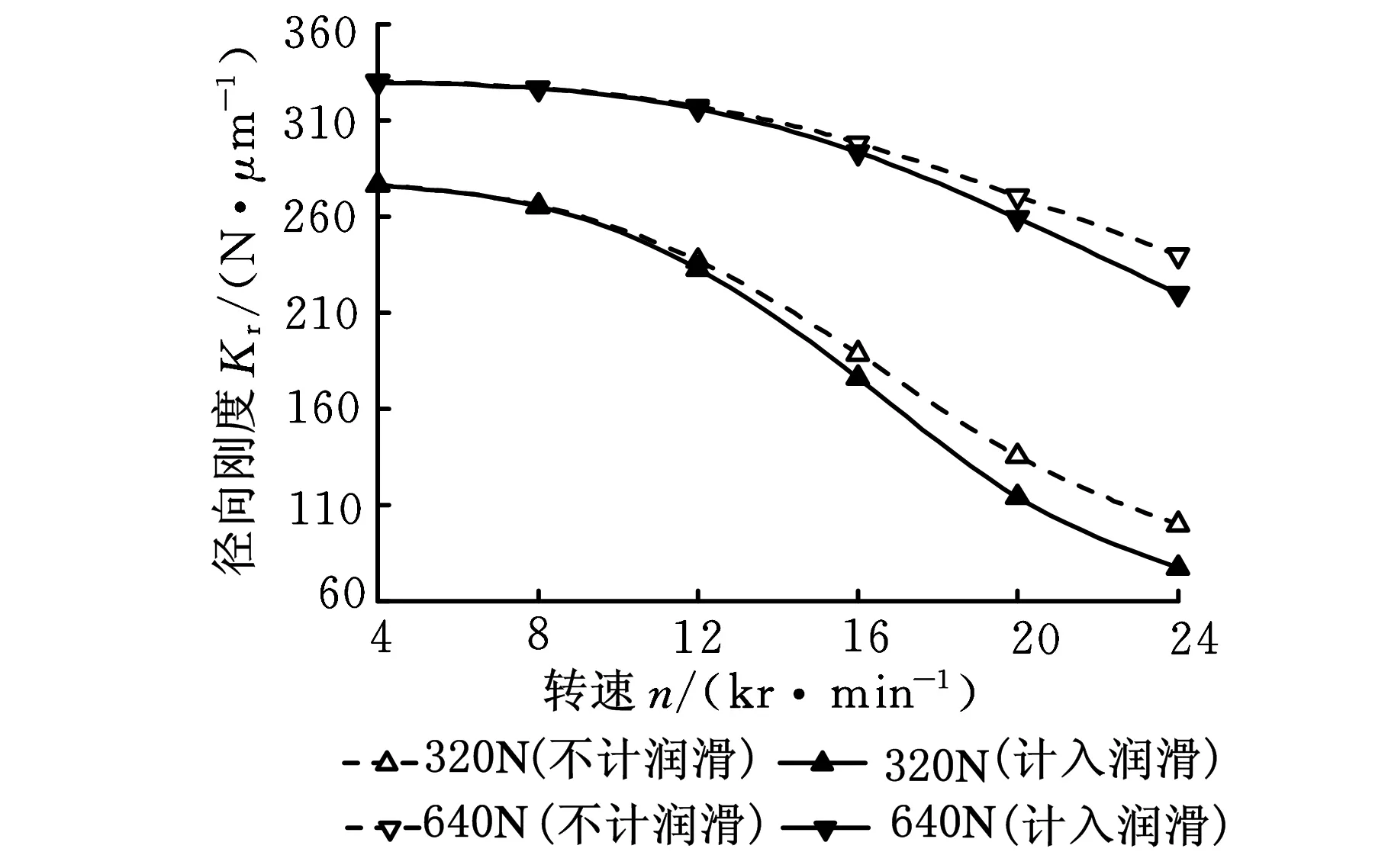
圖10　不同工況下彈流油膜對徑向剛度的影響

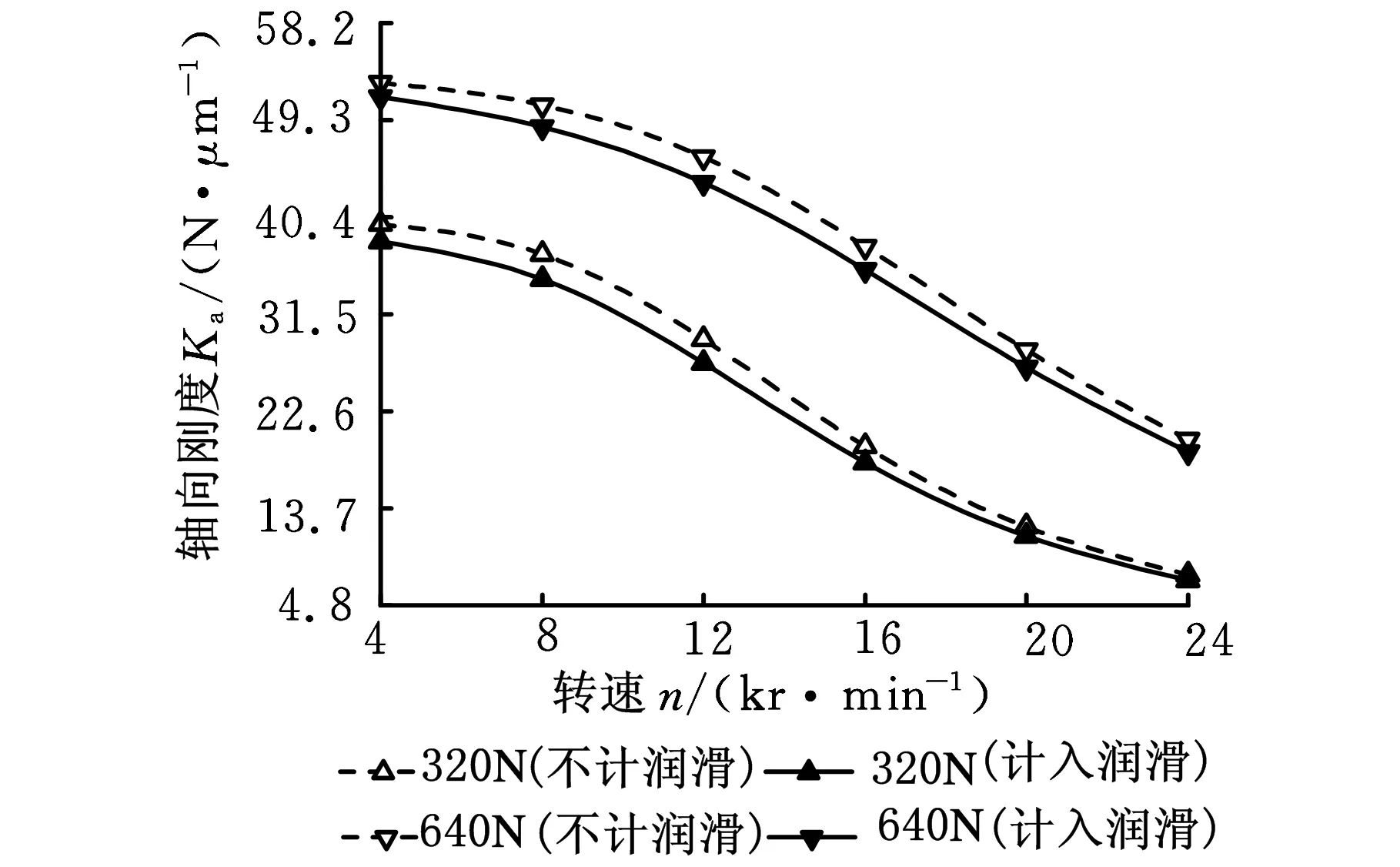
圖11　不同工況下彈流油膜對軸向剛度的影響

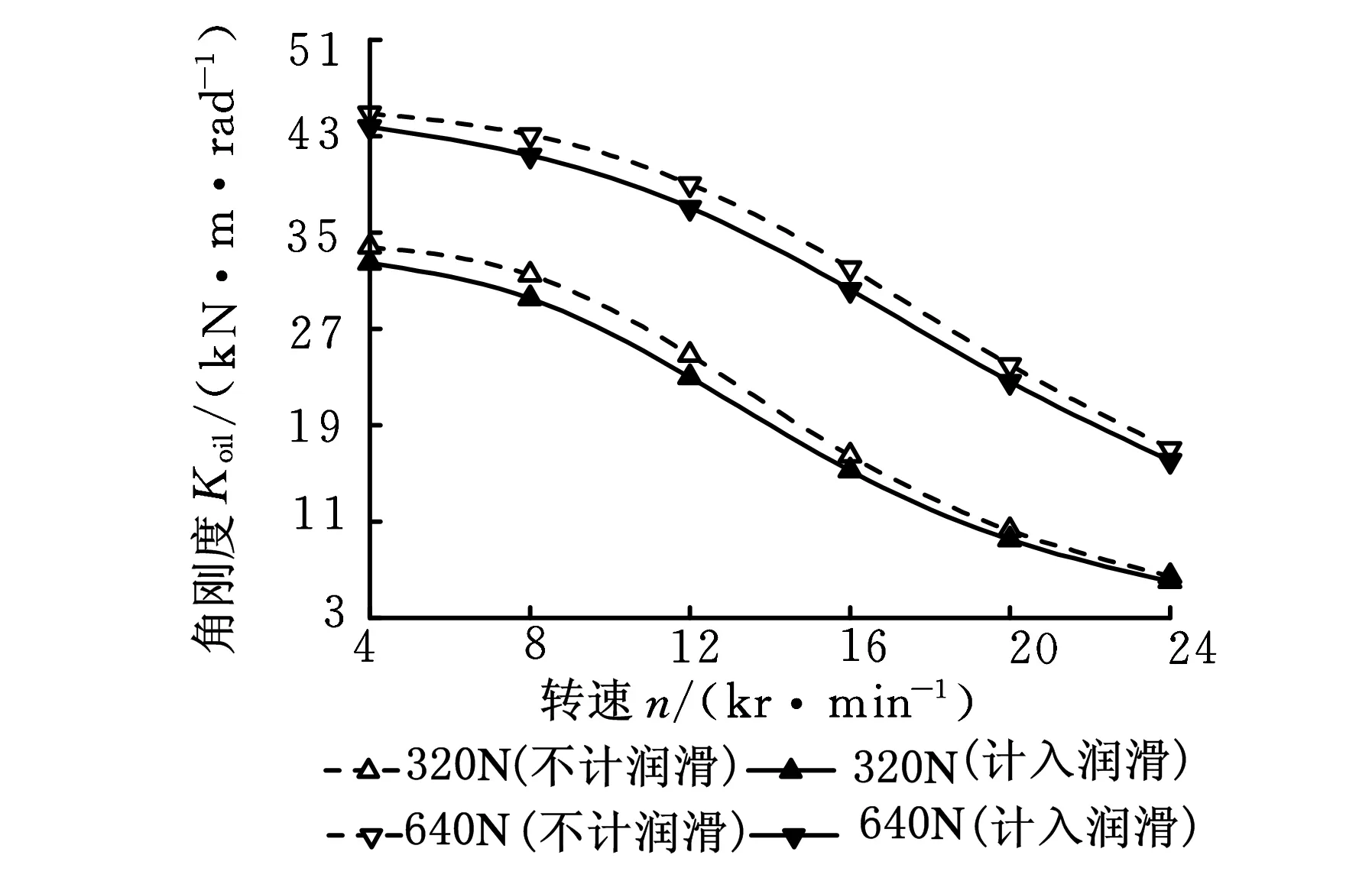
圖12　不同工況下彈流油膜對角剛度的影響

圖11、圖12中，同一速度參數條件下，對于不同預緊力，考慮彈流油膜，軸承軸向剛度和角剛度均有不同程度的減小，但彈流油膜對軸向和角剛度影響較小。

4　結論

(1)建立了計入彈流潤滑、套圈離心力變形和熱變形影響的角接觸球軸承擬靜力學修正模型。該模型不僅可反映套圈變形和彈流潤滑對軸承套圈溝道曲率中心與球心的相對位置的影響規律，而且還可反映動剛度的變化規律，克服了現有模型的不足。

(2)揭示了套圈變形和彈流潤滑隨轉速和預緊力的變化規律及其對動剛度的影響規律。研究發現，轉速提高后，油膜厚度增大，與此同時，套圈和滾動體離心力作用增強，溫升加劇，離心變形增加。提高轉速雖利于實現全膜潤滑，但溫升會加劇套圈熱變形。套圈變形對軸向剛度和角剛度的影響可以忽略不計，但可以增大徑向剛度，進而影響軸承動剛度和壽命。

(3)隨著預緊力的增大,軸承徑向、軸向和角向剛度呈非線性增大。套圈變形在一定程度上可以提高徑向剛度，降低軸向剛度和角剛度，且預緊力越大,套圈變形對軸向剛度和角剛度的影響越明顯。

(4)計入彈流潤滑油膜的影響時，軸承實際剛度比接觸剛度小,由此說明潤滑油勢必會造成支承剛度軟化而降低其支承性能，且轉速越大，彈流潤滑對徑向剛度的影響也越大。

[1]Harris T A.An Analytical Method to Predict Skidding in High Speed Roller Bearing[J]. Wear, 1966, 93:17-21.

[2]羅祝三，孫心德，吳林豐. 滾動軸承在任意方向的支承剛度[J]. 南京航空學院學報，1992，24(3):248-256.

Luo Zhushan, Sun Xinde, Wu Linfeng. Rolling Bearings Stiffness in Arbitrary Direction[J]. Journal of Nanjing Aeronautical Institute,1992,24(3):248-256.

[3]Ali N J,Garcfa J M.Experimental Studies on the Dynamic Characteristic of Rolling Element Bearings[J].Journal of Engineering Tribology,2010,224(9):659-666.

[4]Cao Hongrui,Holkup T,Altintas Y.A Comparative Study on the Dynamics of High Speed Spindles with Respect to Different Preload Mechanisms[J].International Journal of Advanced Manufacturing Technology,2011,57:871-883.

[5]張峻暉,黃紅武,熊萬里.高速電主軸軸承配合過盈量的計算方法研究[J].機械與電子,2004(7):7-10.

Zhang Junhui,Huang Hongwu,Xiong Wanli.Calculation Method Research of the Interference Fit for High Speed Motorized Spindle Bearings[J].Machinery & Electronics,2004(7)：7-10.

[6]Lin Chiwei,Tu J F,Joe K.An Integrated Thermo-mechanical-dynamic Model to Characterize Motorized Machine Tool Spindles During Very High Speed Rotation[J].International Journal of Machine Tool & Manufacture,2003,43:1035-1050.

[7]黃載生,周士森.彈性力學與應用[M].杭州:浙江大學出版社,1989.

[8]蔣興奇,馬家駒,趙聯春.高速精密角接觸球軸承零件熱位移分析[J].軸承,2001(1):5-7.

Jiang Xingji,Ma Jiaju,Zhao Lianchun.Analysis on Heat Displacement of Components of High Speed Precision Angular Contact Ball Bearing,Bearing,2001(1):5-7.

[9]Hamrock B J,Dowson D. Isothermal Elasto-hydrodynamic Lubrication of Point Contacts,Part Ⅲ:Full Flooded Results[J].Journal of Lubrication Technology,Trans.ASEM,1976,98(2):223-229.

[10]李松生,陳曉陽,張鋼,等.超高速時電主軸軸承的動態支承剛度分析[J].機械工程學報,2006,42(11):60-65.

Li Songsheng,Chen Xiaoyang,Zhang Gang,et al.Analyses of Dynamic Supporting Stiffiiess About Spindle Bearings at Extra High-speed in Electric Spindles[J].Chinese Journal of Mechanical Engineering,2006,42(11):60-65.

[11]何曉亮,熊萬里,黃紅武.高速精密主軸軸承熱特性的計算及分析[J].機械,2003,3(9):14-16.

He Xiaoliang,Xiong Wanli,Huang Hongwu.Analysis and Calculation on the Thermal Behavior of Precision High-speed Spindle Bearing[J].Machinery,2003,3(9):14-16.

[12]Gupta P K.Transient Ball Motion and Skid in Ball Bearing[J].Journal of Lubrication Technology,1975,97(2):261-269.

[13]朱益利,金超武,許磊,等.滾珠軸承力學模型的數值求解方法研究[J].中國機械工程,2013,24(4):427-431.

Zhu Yili,Jin Chaowu,Xu Lei,et al.Numerical Solution Methods of Ball Bearing Mechanics Modle[J].China Mechanical Engineering,2013,24(4):427-431.

[14]萬長森. 滾動軸承的分析方法[M]. 北京:機械工業出版,1987.

[15]Mohammed A A,Abdallah A E.Effects of Axial Preloading of Angular Contact Ball Bearing on the Dynamic of a Grinding Machine Spindle System[J].Journal of Materials Processing Technology,2003,136:48-59.

(編輯王艷麗)

Research on Dynamic Stiffness of Ball Bearings Considering Ferrule Deformation and Elastohydrodynamic Lubrication

Xiong WanliZhao ZishengZhou YangLü LangHou Zhiquan

1.National Engineering Research Center for High Efficiency Grinding,Hunan University,Changsha,410082 2.Zhuzhou Lince Group Co. Ltd., Hunan Rail Transportation Cooling Engineering Center,Zhuzhou,Hunan,412001

Aiming at the shortage of traditional quasi-static analytical method which did not consider the changes in geometrical positions of bearing inner raceway curvature center and the rolling body center caused by bearing thermal deformation,the centrifugal force deformation and the elastohydrodynamic lubrication effect,a bearing quasi-static modified model was established considering the effects of ferrule deformation and elastohydrodynamic lubrication.The effects of thermal deformation, the centrifugal force deformation and the lubricating oil film on bearing dynamic stiffness were studied by established model under conditions of different rotational speeds and bearing preloads.The validity of the established model was verified by comparison with the Gupta typical examples and experiments.

angular contact ball bearing; dynamic stiffness; ferrule deformation; elastohydrodynamic lubrication

2015-12-01

國家科技重大專項(2013ZX04012-052)

TH133.33DOI：10.3969/j.issn.1004-132X.2015.11.001

熊萬里,男,1971年生。湖南大學機械與運載工程學院教授、博士研究生導師。主要研究方向為高速電主軸系統動力學、液體靜壓主軸技術、高速大功率電機技術。發表論文70余篇。趙紫生,男,1989年生。湖南大學機械與運載工程學院碩士研究生。周陽,男,1990年生。湖南大學機械與運載工程學院碩士研究生。呂浪,男,1977年生。湖南大學機械與運載工程學院講師。侯志泉,男,1980年生。株洲聯誠集團有限責任公司工程師、博士。