基于奇異值融合的機械設備盲信息提取

毋文峰　李　浩　朱　露

1.中國人民武裝警察部隊警官學院,成都,6102132.第二炮兵工程大學,西安,710025

基于奇異值融合的機械設備盲信息提取

毋文峰1,2李浩1朱露2

1.中國人民武裝警察部隊警官學院,成都,6102132.第二炮兵工程大學,西安,710025

針對機械設備的故障特征信息提取問題，提出了基于奇異值融合的機械盲信息提取方法。首先,由機械振動測量信號分離振動源信號，并進行包絡解調組成包絡信號矩陣，進而進行奇異值分解,提取矩陣的奇異值均值和奇異值熵作為故障特征信息;然后,針對分離矩陣直接進行奇異值分解，提取奇異值作為故障特征信息；最后，將包絡信號矩陣奇異值均值、奇異值熵和分離矩陣奇異值進行特征層信息融合作為機械設備的故障特征信息。將該方法應用于液壓齒輪泵可以有效地提取機械設備盲特征信息。

盲源分離；獨立成分分析；包絡分析；奇異值分解；特征提取

0　引言

盲源分離(blind source separation,BSS)[1-6]作為一種預處理手段，可以從機械設備測量信號中分離(或恢復)出各個機械部件的振動源信號。目前,盲源分離方法,如獨立成分分析(independent component analysis,ICA)法,已在機械設備故障診斷領域取得了初步的應用。

在機械設備盲信號處理中,目前的方法大多是基于分離源信號來提取故障特征信息并進行故障診斷[3-6],而很少從分離矩陣出發來處理。但是從信息的角度來看，分離源信號和分離矩陣是從兩個不同的角度和層面來闡釋機械設備故障特征信息的，它們各有側重。在一定意義上,分離矩陣包含的信息與源信號的信息是互補的，它們共同表征了機械設備的狀態。若將分離源信號和分離矩陣包含的信息互相融合，則必然能夠更全面、更深刻地表征其狀態。因此，本文將盲信號處理、包絡分析、奇異值分解和信息熵等信號處理方法相結合，提出基于奇異值融合的故障特征信息提取方法，從分離源信號和分離矩陣融合的角度來提取機械設備的故障特征信息,并將其應用于液壓齒輪泵的故障特征信息提取中。

1　基本概念和理論

1.1包絡分析

包絡分析(envelope analysis,EA)[7-11],又稱解調分析,目的是提取載附在高頻調制信號上的與故障有關的低頻信號,從時域上看,就是提取時域信號波形的包絡軌跡。包絡分析是目前最常用、最有效的機械設備故障診斷方法之一。調制信號的包絡解調方法主要有三種：Hilbert幅值解調法、檢波-濾波解調法和高通絕對值解調法。Hilbert幅值解調法由于簡單、有效，故在齒輪和滾動軸承等機械信號處理中已應用較多[12],本文也利用Hilbert幅值解調法來提取源信號的上下包絡信號。

1.2奇異值分解

設有M行N列的實矩陣A，它可以作奇異值分解(singular value decomposition,SVD)[13-14],若有

X=UΛVT

(1)

U=[u1u2…uM]∈RM×M

UTU=I

V=[v1v2…vN]∈RN×N

VTV=I

則U和V分別稱為實矩陣A的左右奇異陣。Λ為矩陣[diag(σ1,σ2,…,σp):0]或其轉置,Λ∈RM×N,p=min(M,N),σ1≥σ2≥…≥σp≥0,σ1,σ2,…,σp稱為實矩陣A的奇異值。

可進行奇異值分解是矩陣的固有特征，矩陣奇異值具有比較高的穩定性，即當矩陣元素發生小的變動時，矩陣的奇異值變化很小；同時矩陣的奇異值還具有比例不變性、旋轉不變性和可降維壓縮等特性。因此，矩陣的奇異值符合機械故障診斷學對于故障特征信息的基本要求。

1.3奇異值熵

為了定量地描述矩陣奇異值的變化程度，引入信息熵理論，根據信息熵的定義來提出并構造奇異值熵。

假設奇異值統一編號為σ1、σ2、…、σn，對其進行歸一化處理，即可得到:

(2)

其中，E=σ1+σ2+…+σn，從而有

(3)

這符合計算信息熵的初始歸一化條件，根據信息熵理論，構造奇異值熵為

(4)

2　基于奇異值融合的盲信息提取方法

2.1盲信息提取策略

2.1.1源信號包絡矩陣奇異值

在機械故障診斷中，齒輪和滾動軸承等部件的振動信號是調制類型信號，而且傳感器測量的信號是這些振動信號的混合信號，這就大大增加了故障特征信息提取的難度，使得故障特征信息的準確度降低。盲源分離技術可以從已知的混合信號(測量信號)中分離(或恢復)出各個振動信號(源信號)，這些源信號提供了較“純”的信息載體，可以從中提取更為準確的故障特征信息。進一步，振動源信號是調制信號，其上下包絡更集中地攜帶了機械設備的運行狀態信息，因此，分離源信號進行包絡解調可以得到上下包絡信號,進而,上下包絡信號可以分別組成上下包絡信號矩陣，稱為初始特征向量矩陣，它們可以準確地刻畫振動源信號的特征信息。若將初始特征向量矩陣進行奇異值分解，則可提取其奇異值作為機械設備的初始故障特征信息。

一般,盲源分離得到的源信號有多個,因此其上下包絡信號矩陣的維數也比較大，這使得包絡矩陣的奇異值比較多，導致后續模式識別的復雜性和計算量也大幅增加。為了減少奇異值數量和計算量，同時又不損失或少損失故障特征信息,考慮對奇異值進行降維壓縮，將上下包絡矩陣奇異值的均值和奇異值熵，作為降維的故障特征信息。

2.1.2盲源分離矩陣奇異值

在盲源分離中，分離(或恢復)源信號相當于估計分離矩陣；當分離矩陣確定了，源信號也就很容易得到。若從信息的角度來看，機械設備的部分故障特征信息不僅包含在分離源信號中，也包含在分離矩陣中，源信號和分離矩陣是從兩個不同的角度和層面來闡釋機械設備故障特征信息的。因此，可將分離矩陣直接作為初始特征向量矩陣進行奇異值分解，并從中提取機械設備的故障特征信息。

2.1.3基于奇異值融合的特征信息提取

在一定意義上,源信號是從宏觀現象來表征機械設備的故障特征信息的，而分離矩陣則是從微觀結構來刻畫機械設備的故障特征信息的，它們是從兩個不同的角度和層面來闡釋同一機械設備的故障特征信息的。若從信息融合的角度來考慮，可將源信號包絡矩陣奇異值(均值和奇異值熵)和分離矩陣奇異值融合共同作為機械設備的故障特征信息，這必然能夠更全面和深刻地表征機械設備的運行狀態信息。

2.2盲信息提取流程和步驟

綜上所述，本文提出的基于奇異值融合的機械盲信息提取方法，即將源信號包絡矩陣奇異值均值、奇異值熵和分離矩陣奇異值進行特征層信息融合，共同作為機械設備的故障特征信息。它的流程如圖1所示。具體步驟為：

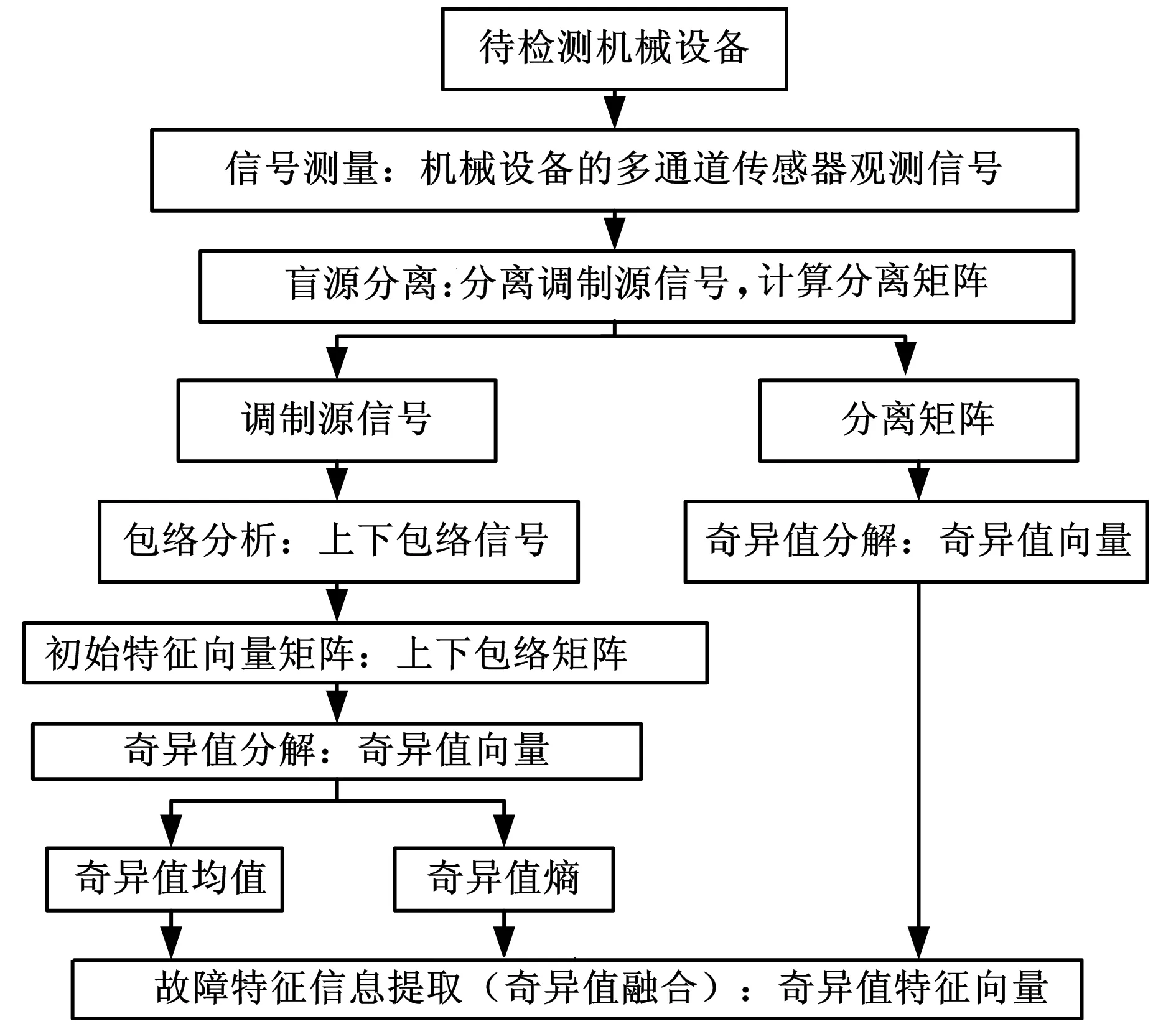
圖1　基于奇異值融合的盲信息提取方法

(1)機械信號測量。從待檢測機械設備上測得多通道傳感器觀測信號(混合信號)。

(2)盲源分離。混合信號經中心化和白化等預處理，利用盲源分離技術(例如FastICA算法等)計算分離矩陣，并分離調制源信號。

(3)源信號包絡矩陣奇異值。利用Hilbert幅值解調法提取調制源信號的上下包絡信號，進而組成初始特征向量矩陣，進行奇異值分解，計算奇異值均值和奇異值熵。

(4)分離矩陣的奇異值分解。分離矩陣進行奇異值分解，得到它的奇異值。

(5)奇異值融合。源信號包絡矩陣奇異值

(均值和奇異值熵)和分離矩陣奇異值進行融合，共同作為機械設備的故障特征信息。

3　液壓齒輪泵試驗

為了驗證該方法的有效性，將其應用于國產CB-Kp63型液壓齒輪泵中。齒輪泵試驗臺架和加速度計(傳感器)的設置如圖2所示，其中，泵軸轉速為定速1480 r/min。

圖2　液壓齒輪泵試驗臺架及加速度計設置

在密閉實驗室環境下,設定齒輪泵故障模式類型包括:正常狀態、齒面磨損和軸承故障；在每個故障模式下各測量64組傳感器觀測信號x(t)=(x1(t),x2(t),x3(t),x4(t))T，即每個故障模式均為64組4通道混合信號，其中，泵殼振動信號采樣頻率設為10 kHz，采樣時間設為1 s。圖3為其中一組混合信號的時域波形。

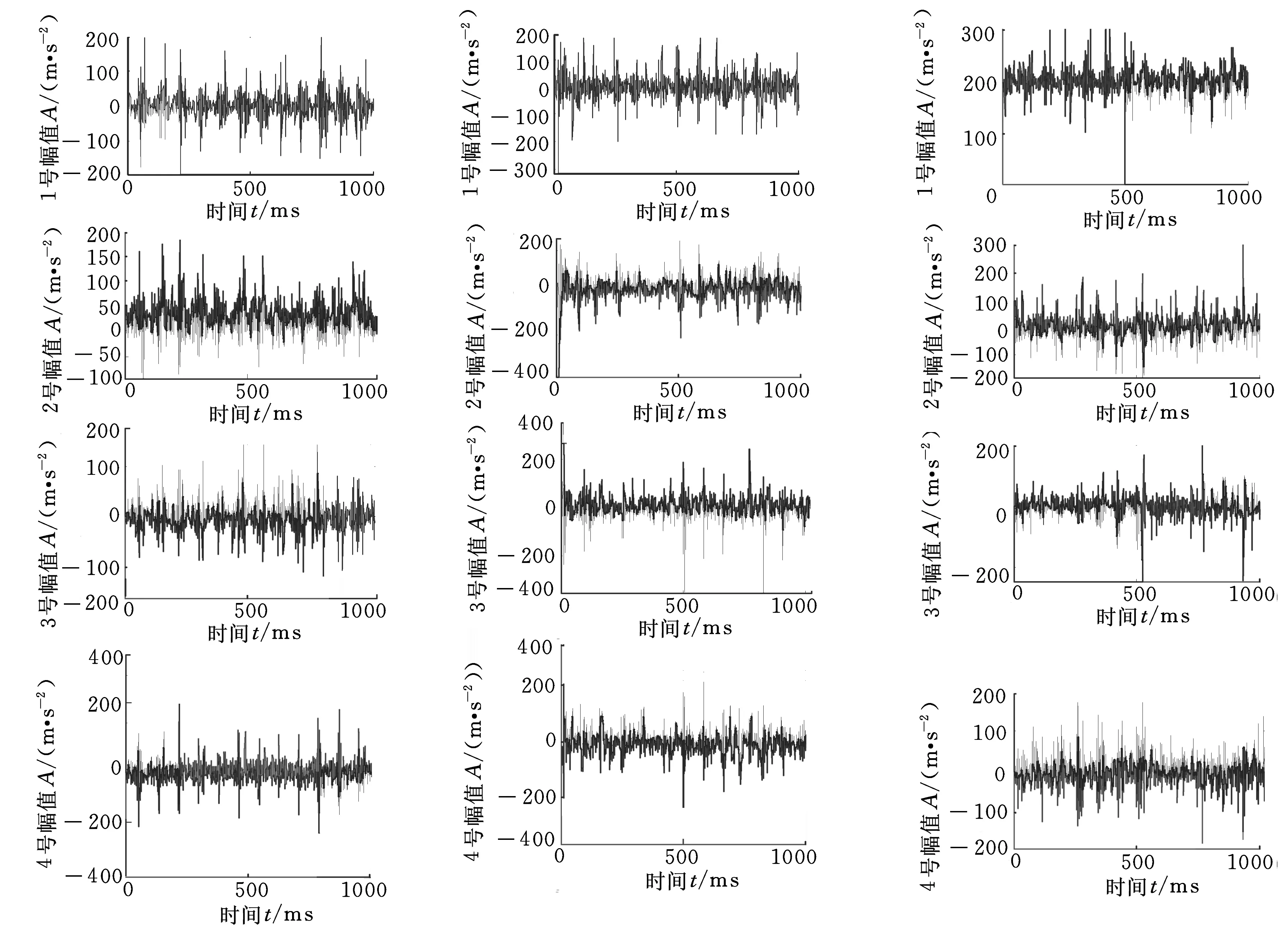
(a)正常狀態 (b)齒面磨損(c)軸承故障圖3　液壓齒輪泵的混合信號時域波形

混合信號x(t)經中心化和白化等預處理,再利用FastICA算法進行盲源分離，可以得到分離矩陣W和源信號s(t),s(t)=(s1(t),s2(t),s3(t),s4(t))T。圖4a、圖5a、圖6a即為圖3混合信號x(t)對應源信號s(t)的時域波形。進一步,源信號進行包絡解調可以提取其上下包絡信號(圖4～圖6)。

同時,分離矩陣W進行奇異值分解也可以提取故障特征信息。例如,由圖3混合信號x(t)可以得到它的分離矩陣：Wnormal(正常狀態)、Wgear(齒面磨損)和Wbearing(軸承故障)，它們再進行奇異值分解可以得到對應的奇異值向量：

λnormal=(0.1897，0.1776,0.1702，0.1429)

λgear=(0.1538,0.1484,0.1434,0.1212)

λbearing=(0.1633，0.1552，0.1459，0.1287)

分析和比較上述奇異值數值,可以得出如下

結論：

(1)與源信號上下包絡矩陣的奇異值向量(初始特征向量)相比,奇異值均值和奇異值熵的聚類劃分特性更為典型，其數值穩定性也更為魯棒。

(2)源信號包絡矩陣的奇異值熵可以定量地表征齒輪泵的運行狀態信息，在同一泵軸轉速下，齒輪泵奇異值熵值從小到大的排列順序依次為：正常狀態、軸承故障、齒面磨損。

(3)盲源分離矩陣的奇異值同樣也具有類間差異顯著而類內聚類集中的良好特性。

(4)與單獨的源信號包絡矩陣奇異值或分離矩陣奇異值相比，融合的奇異值特征信息向量可以更全面、更準確地表征齒輪泵的故障特征信息，因而具有更為優良的故障特征信息刻畫性能。

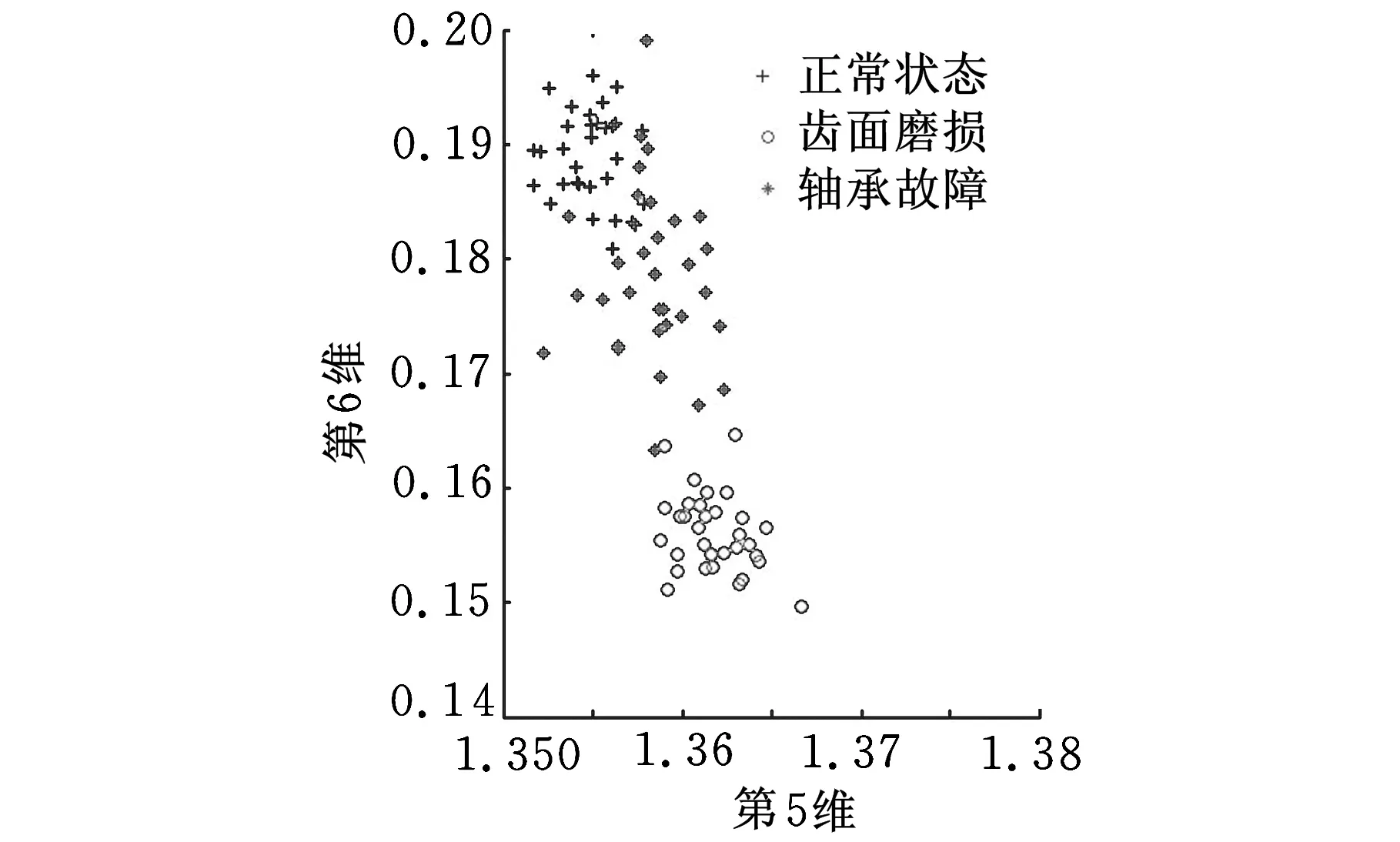
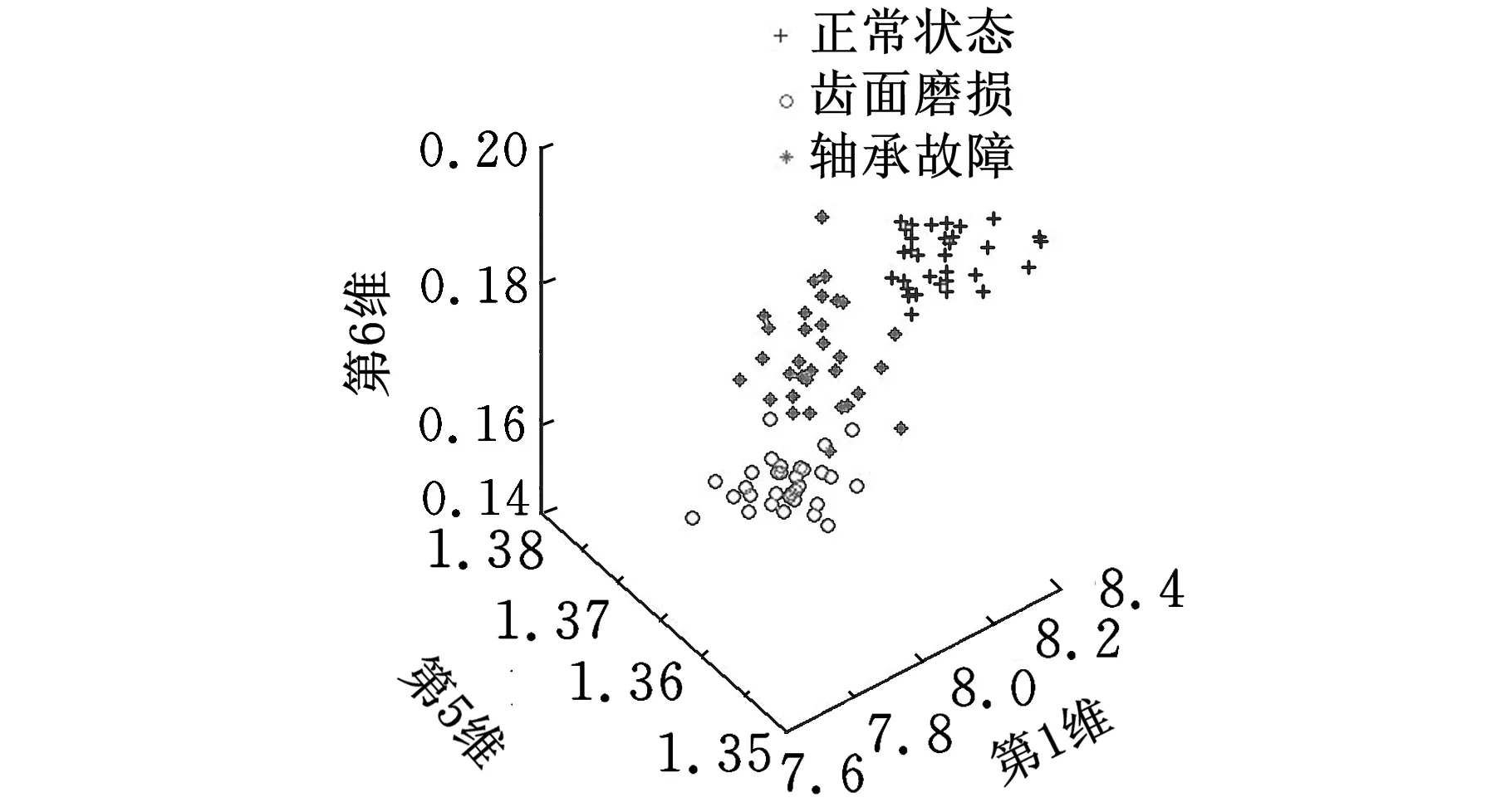
奇異值特征信息向量的分布如圖7所示。由于奇異值特征信息向量是一個9維向量，不易直觀觀察，因此,這里僅給出了它的2D平面分布(第5維和第6維)和3D空間分布(第1維、第5維和第6維)。

由圖7可知，基于奇異值融合的機械盲信息提取方法是可行的，也是有效的。

(a)源信號 (b)上包絡信號(c)下包絡信號圖4　液壓齒輪泵的源信號和上下包絡信號時域波形(正常狀態)

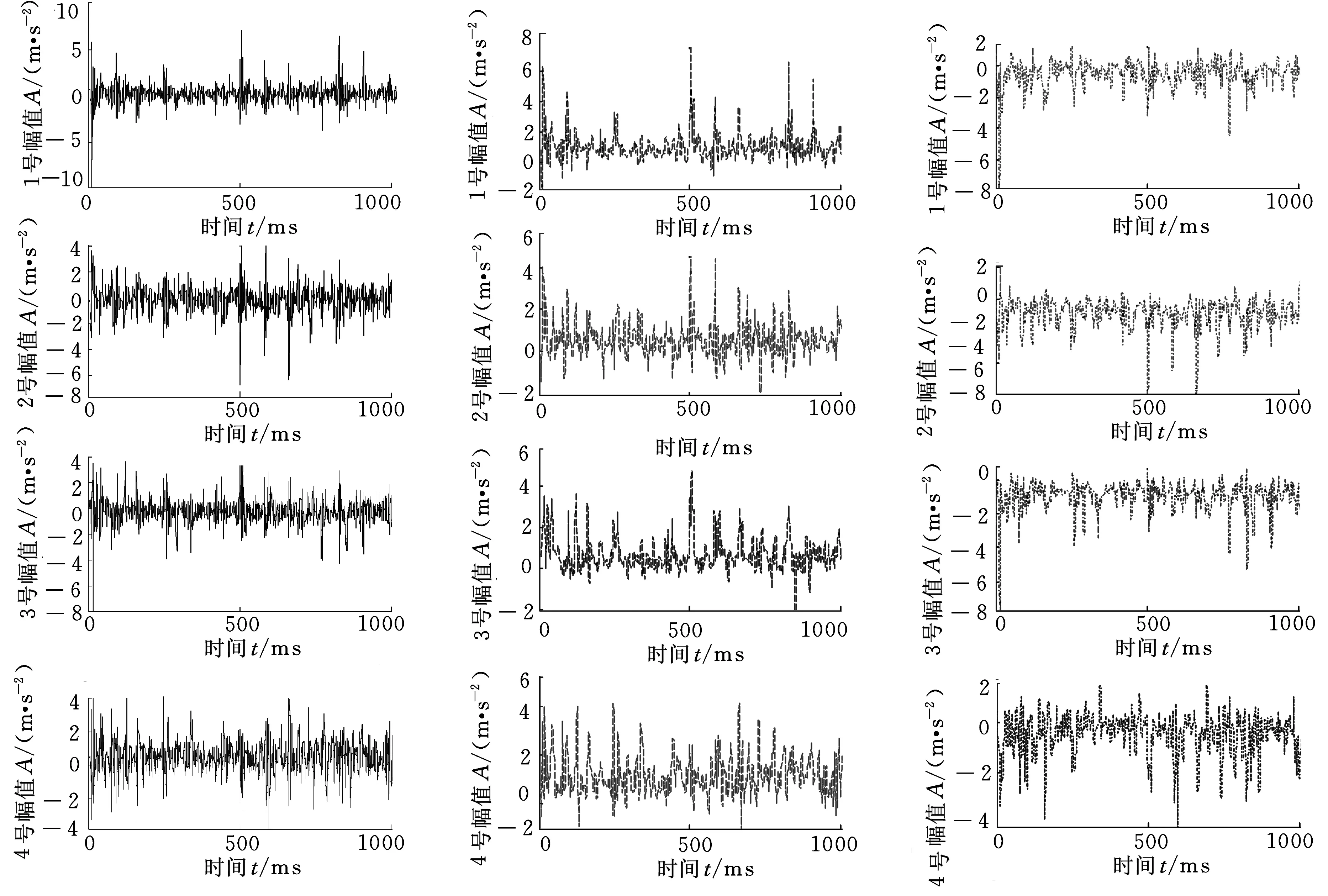
(a)源信號 (b)上包絡信號(c)下包絡信號圖5　液壓齒輪泵的源信號和上下包絡信號時域波形(齒面磨損)

(a)2D

(b)3D圖7　奇異值特征信息向量分布(2D和3D)

4　結語

在機械盲信號處理中，分離源信號和分離矩陣是從兩個不同的角度和層面來闡釋機械設備故障特征信息的，它們各有側重，互為補充。本文將分離源信號和分離矩陣包含的故障特征信息相融合，提出基于奇異值融合的機械盲信息提取方法，并利用液壓齒輪泵試驗驗證了該方法的可行性和有效性。

[1]Hyvarinen A, Oja E. Independent Component Analysis: Algorithms and Applications[J]. Neural Networks,2000,13(4/5):411-430.

[2]Hyvarinen A, Karhunaen J,Oja E.Independent Component Analysis[M].New York:John Wiley & Sons,Inc.,2001.

[3]Tse P W, Zhang J Y,Wang X J.Blind Source Separation and Blind Equalization Algorithms for Mechanical Signal Separation and Identification[J].Journal of Vibration and Control,2006,12:395-423.

[4]Zhou W L,Chelidze D.Blind Source Separation Based Vibration Mode Identification[J].Mechanical Systems and Signal Processing,2007,21:3072-3087.

[5]胥永剛,李強,王正英,等.基于獨立分量分析的機械故障信息提取[J].天津大學學報,2006,39(9):1066-1071.

Xu yonggang,Li Qiang,Wang Zhengying,et al.Fault Information Extraction of Mechanical Equipment Based on Independent Component Analysis[J].Journal of Tianjin University,2006,39(9):1066-1071.

[6]毋文峰,陳小虎,蘇勛家,等.基于負熵的旋轉機械盲信號處理[J].中國機械工程,2011,22(10):1193-1197.

Wu Wenfeng,Chen Xiaohu,Su Xunjia,et al.Blind Signal Processing Based on Negentropy for Rotating Machines[J].China Mechanical Engineering,2011,22(10):1193-1197.

[7]Tse P W,Peng Y H,Yam R.Wavelet Analysis and Envelope Detection for Rolling Element Bearing Fault Diagnosis-their Effectiveness and Flexibilities[J].Journal of Vibration and Acoustics,2001,123:303-310.

[8]Szwoch G,Czyzewski A,Kulesza M. A Low Complexity Double-talk Detector Based on the Signal Envelope[J].Signal Processing,2008,88:2856-2862.

[9]Sheen Y T. An Analysis Method for the Vibration Signal with Amplitude Modulation in a Bearing System[J].Journal of Sound and Vibration,2007,303:538-552.

[10]Sheen Y T.On the Study of Applying Morlet Wavelet to the Hilbert Transform for the Envelope Detection of Bearing Vibrations[J].Mechanical Systems and Signal Processing,2009,23:1518-1527.

[11]Shi D F,Wang W J,Qu L S.Defect Detection for Bearings Using Envelope Spectra of Wavelet Transform[J].Journal of Vibration and Acoustics,2004,126:567-573.

[12]Feldman M.Analytical Basics of the EMD:Two Harmonics Decomposition[J].Mechanical Systems and Signal Processing,2009,23:2059-2071.

[13]Horn R A, Johnson C R.Matrix Analysis,Cambridge[M].Cambridge:Cambridge University Press,1985.

[14]Yang W X,Tse P W.Development of an Advanced Noise Reduction Method for Vibration Analysis Based on Singular Value Decomposition[J].Journal of NDT&E International,2003,36:419-432.

(編輯王艷麗)

Blind Mechanical Information Extraction Based on Singular Value Fusion

Wu Wenfeng1,2Li Hao1Zhu Lu2

1.Officers College of Chinese Armed Police Force,Chengdu,610213 2.The Second Artillery Engineering University,Xi’an,710025

In order to extract the fault feature informations of mechanical equipment,a blind information extraction method was proposed based on singular value fusion.Firstly,by independent component analysis,the source signals were separated from mechanical vibration observation signals.Then the source signals were demodulated to get envelope signals and form envelope matrixes.The envelope matrixes were processed by singular value decomposition and then the singular value vectors (including singular value averages and singular value entropy) were extracted as feature information of the detected mechanical equipment. Secondly, the separating matrix was directly processed by singular value decomposition and its singular values could also be extracted as useful feature information. Lastly, the singular value vector was obtained by information fusion as final optimum feature information of the mechanical equipment. The experimental results of hydraulic gear pump indicate that this method can be applied to feature extraction of mechanical equipment effectively.

blind source separation;independent component analysis;envelope analysis;singular value decomposition;feature extraction

2014-06-03

國家自然科學基金資助項目(61132008)

TH165.3;TP391.4DOI：10.3969/j.issn.1004-132X.2015.22.008

毋文峰,男,1978年生。中國人民武裝警察部隊警官學院管理科學與工程系講師,第二炮兵工程大學博士。主要研究方向為系統工程,智能信號處理。出版專著1部,發表論文20余篇。李浩,男，1984年生。中國人民武裝警察部隊警官學院管理科學與工程系講師。朱露,女,1977年生。第二炮兵工程大學網絡中心高級工程師。