基于解耦消參的動對動相對定位算法

伍勁實，趙修斌，龐春雷，余永林，劉 明

（空軍工程大學信息與導航學院，陜西西安710077）

基于解耦消參的動對動相對定位算法

伍勁實，趙修斌，龐春雷，余永林，劉 明

（空軍工程大學信息與導航學院，陜西西安710077）

針對動對動相對定位基線參量實時可變導致模糊度難以準確求解的問題，在比較分析動對動與靜態相對定位區別與聯系的基礎上，提出了基于解耦消參的動對動相對定位算法。該算法將解耦法與最小二乘模糊度降相關平差（LAMBDA）算法相結合，采用解耦法變換雙差載波相位觀測方程，從而消除基線參量并實時推算雙差整周模糊度的浮點解及其協方差矩陣，然后利用LAMBDA算法對模糊度進行固定和確認。試驗結果表明，基于解耦消參的動對動相對定位算法初始化模糊度用時較短，在70 s左右即可正確解算出動態單頻整周模糊度，獲得了厘米級的相對定位結果，適用于短基線高精度動態相對定位。

動對動；相對定位；整周模糊度；解耦；LAMBDA

0 引言

動對動高精度相對定位的關鍵是在動態情況下快速準確地確定整周模糊度［1］。由于動對動相對定位基線矢量實時可變，屬于變參數估計問題，且難以找到附加約束條件進行輔助［2-3］，因此其整周模糊度及其協方差矩陣的初始化過程相比于靜態更為復雜。目前常用的模糊度浮點解求解方法主要有最小二乘法、遞推最小二乘法、卡爾曼濾波法［4］、雙頻載波相位的直接解法［5］、矩陣解耦法［6］等，其中能夠適用于動態相對定位的方法主要是最小二乘法、卡爾曼濾波法和矩陣解耦法。最小二乘法屬于批處理算法，難以滿足動態相對定位的實時性要求，且計算量大；卡爾曼濾波法對動態模型的建立要求較高，若模型的建立與實際運動狀態不符合，則待估參量的精度難以達到要求，進而難以實現高精度相對定位；文獻［6］提出了基于矩陣解耦的模糊度逼近搜索法，該方法能夠較好地用于模糊度浮點解及其協方差矩陣的實時推算，但其對模糊度浮點解的精度要求較高，需要較長的時間才能逼近模糊度真值。本文針對此問題，在比較分析靜態與動態相對定位區別與聯系的基礎上，提出了基于解耦消參的動對動相對定位算法。

1 傳統相對定位模糊度求解

在短基線條件下，雙差載波相位觀測方程為：

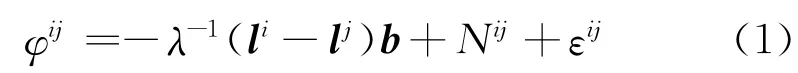
其中，φij為雙差載波相位觀測量，λ為載波波長，l為接收機至衛星的單位矢量，b=bxbyb（ ）zΤ為基線矢量，Nij為雙差整周模糊度，εij為雙差測量噪聲。

若參考站與移動站相對靜止，第k個歷元觀測到n顆衛星，可構造n—1個雙差觀測方程，忽略雙差噪聲，將式（1）變為方程組形式可得

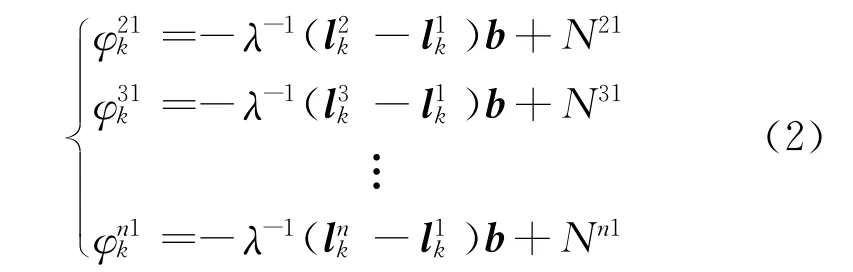
將k個歷元雙差觀測方程進行組合，可得到k×（n—1）個雙差方程：

由于方程組中含有（n—1）+3=n+2個未知參量，只需要滿足條件k×（n—1）≥n+2，即可用最小二乘法求解基線矢量和雙差整周模糊度的浮點解。但由于觀測時間較短會造成法矩陣的病態性［7］，因此靜態相對定位時，往往通過增加觀測時間來獲得高精度定位結果；同時由于測站之間相對靜止，通常可精確測量測站間基線長度，將其作為已知約束條件輔助解算整周模糊度［8］，提高定位精度和效率。在求解得到模糊度浮點解的前提下，可利用LAMBDA算法對模糊度進行搜索與固定，模糊度一旦正確固定，則可將其帶入雙差方程反解出基線矢量，實現高精度相對定位。這種在靜態情況下求解模糊度的方法一般稱為整周模糊度的靜態初始化。當前，高精度動態相對定位往往也是采用靜態初始化的方法，即在靜態情況下固定住模糊度，然后再開始運動，但這樣不適用于動態情況下的實時解算，因此需要尋求模糊度的動態初始化方法。

2 基于解耦消參的動對動相對定位算法

2.1 動對動模糊度求解特點

在動對動情況下，如果正確解算出模糊度，且不發生周跳和衛星失鎖的情況，則雙差模糊度參量N不隨時間的變化而變化，但由于運載體之間的相對位置實時變化，式（1）中的基線矢量參量b隨時間實時變化。將k個歷元的雙差觀測方程進行組合，則式（3）變為式（4）。

由式（4）可知，每一個歷元均會增加3個未知基線矢量參量，則k個歷元得到的方程組中包含3k+n—1個未知參量，此時需要滿足條件k×（n—1）≥3k +n—1；而且隨著觀測時間的增加，未知參量個數線性增加，觀測方程系數矩陣維數越來越大，傳統的最小二乘法用于靜態定位時，模糊度初始化需要至少2 min，如果將其用于動對動，則會產生至少360個未知基線參量，此時將難以利用最小二乘求解，同時，基線矢量實時變化，難以再作為已知約束條件進行輔助，這時應尋求適合于動態情況下的模糊度初始化方法。

由于在實際求解雙差模糊度過程中，對于基線矢量bk并不關心，因為一旦準確求解并固定雙差模糊度，基線矢量就能精確求得。為了滿足動對動對實時性的要求，并且充分利用每一歷元的觀測信息，本文采用基于解耦消參的動對動相對定位算法求解動對動模糊度。

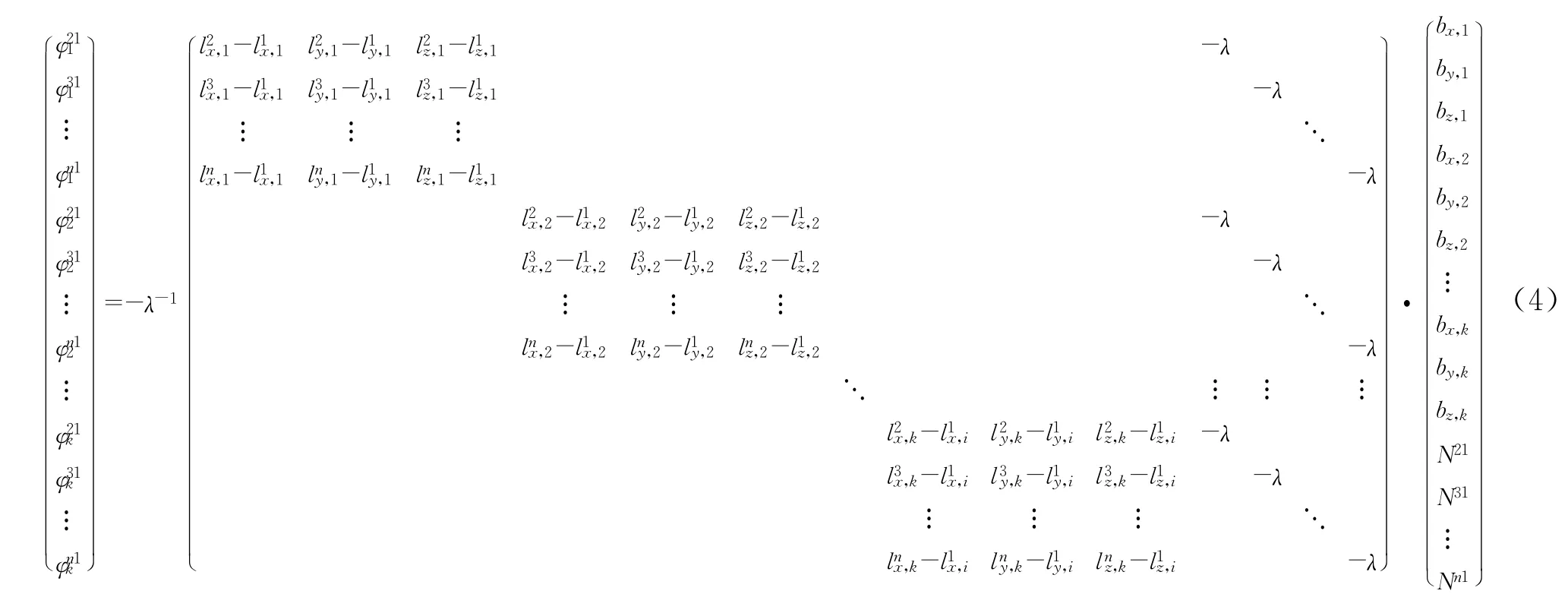
2.2 動對動相對定位算法

解耦法的基本思想為：將每一歷元的基線矢量參量bk用雙差模糊度參數N表示，從而消除bk，只剩下N，進而僅對雙差模糊度進行推算［9］。

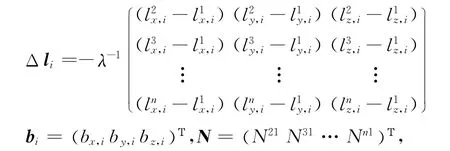
則第k個歷元雙差方程為

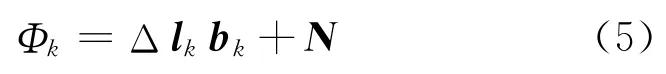
基線矢量的最小二乘解為

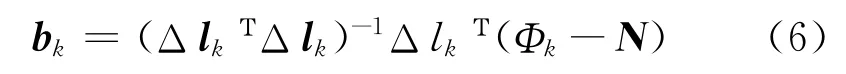
根據式（5），對前n個歷元得到的雙差觀測方程疊加得到

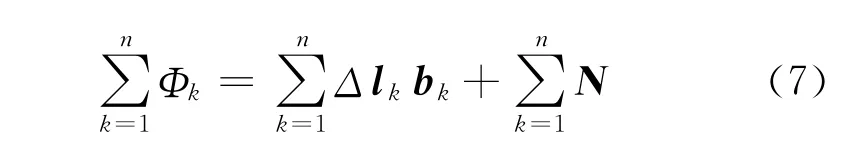
將式（6）代入式（7）得

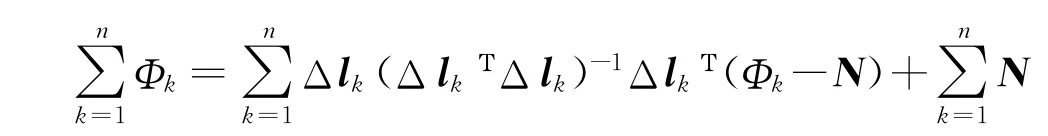
則有

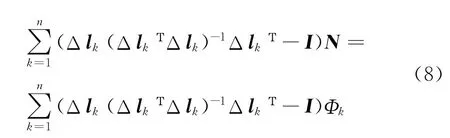
則模糊度浮點解可表示為：

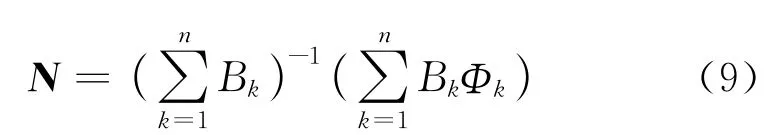
根據誤差傳播定律，可求得模糊度的協方差矩陣為：

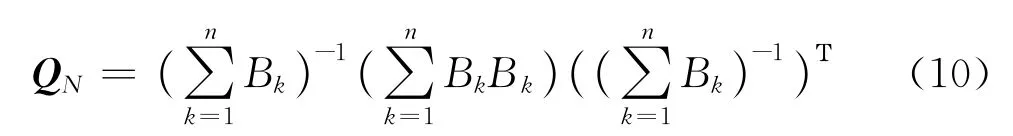
式（9）和式（10）即為解耦法推算模糊度浮點解及其協方差矩陣的公式。

經分析可知，采用解耦法實時推算模糊度浮點解及其協方差矩陣，是將當前時刻之前每一歷元的觀測信息進行求和，隨著觀測時間的增加，并沒有造成矩陣維數的增加。在用解耦法得到雙差模糊度浮點解及其協方差矩陣的基礎上，利用LAMBDA［10］算法進行模糊度的搜索與固定，從而獲得高精度動對動相對定位結果，滿足動對動相對定位的實時性要求。

從式（9）和式（10）中可以看出，在忽略觀測噪聲的情況下，雙差模糊度浮點解的求解僅與載波相位觀測值、接收機至衛星的方向矢量以及載波波長有關，而接收機的運動狀態雖然對接收機的捕獲、跟蹤性能影響較大，但對接收機至衛星的方向矢量影響較小，理論上，只要接收機能連續跟蹤衛星信號，提供可靠的載波相位觀測值，則該算法就具有適用性。

3 試驗結果與分析

3.1 試驗方法

本文從兩個方面驗證該算法的可行性：1）如果整個觀測過程不發生周跳，那么動態整周模糊度應與靜態整周模糊度相同，基于這一思想，先用傳統成熟的方法解算出靜態時的模糊度，將其作為參考值，結果如表1所示，然后用基于解耦消參的動對動相對定位算法對動態情況下獲得的觀測數據進行解算，將求解得到的動態模糊度與參考值作比較，若該算法可行，則二者應該一致。2）利用基于解耦消參的動對動相對定位算法求解得到的動態模糊度反解基線長度，將結果與其實際長度進行比較，期望獲得較小的基線誤差。

表1 靜態時解算出的雙差整周模糊度參考值Tab.1 Referencevaluefordoubledifference integerambiguityinstaticcalculation

若能同時獲得以上兩個預期效果，則說明所提算法能較好地適用于動態相對定位。

3.2 試驗條件

為驗證該算法的準確性和可行性，采用固定基線情況下動態試驗的方法。利用兩個NovAtel接收機，基準站和移動站分別為SPAN-CPT和OEM628板卡，均連接GPS-703-GGG型號的雙頻天線，數據采樣率為1Hz，兩天線固定于已知長度的基線兩端，并放置于小車前端，試驗前已測得基線長為1.91m，取衛星截止高度角為15°，觀測到7顆GPS衛星，分別為PRN3，PRN14，PRN20，PRN22，PRN25，PRN31，PRN32，選取PRN3作為參考衛星。先靜態觀測大約10min，然后開始動態試驗，運動速度約為3m/s，繞操場運動大約5min。

3.3 試驗過程

采用解耦法對動態數據推算約1min，這里以雙差模糊度N31為代表（其他雙差模糊度的變化與解算情況與之類似），其浮點解在推算中逼近真值的過程如圖1所示；然后采用LAMBDA算法固定每一歷元的雙差模糊度，表2和圖2為N31在每一歷元的固定結果；利用固定得到的雙差模糊度反解每一歷元的基線長度，所得結果如圖3所示；將求解得到的基線長度與實測長度相比較，得到基線誤差曲線圖如圖4所示。

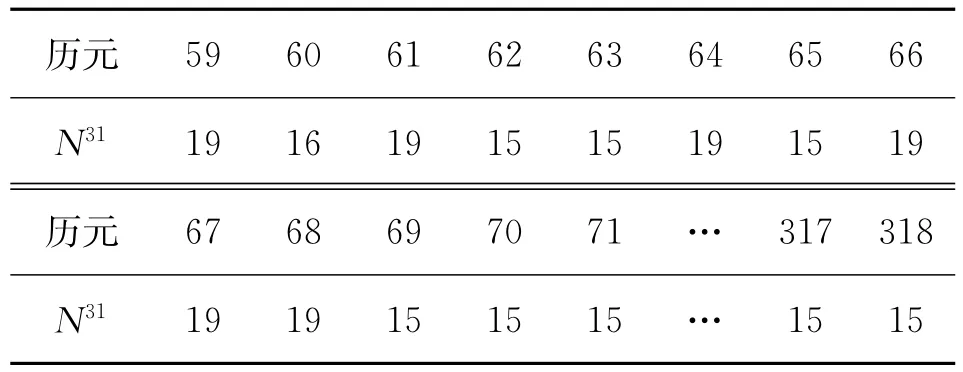
表2 雙差模糊度N31在每一歷元的固定結果Tab.2 Thefixedresultfordoubledifference ambiguityN31ineachepoch

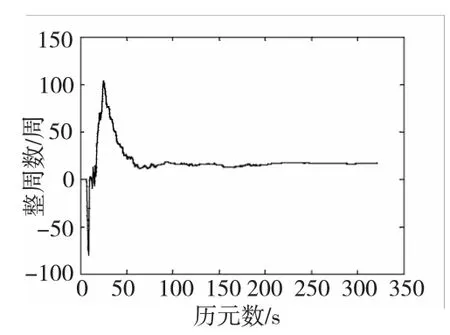
圖1 模糊度浮點解N31逼近真值的過程Fig.1 FloatsolutionN31 approachingrealvalue

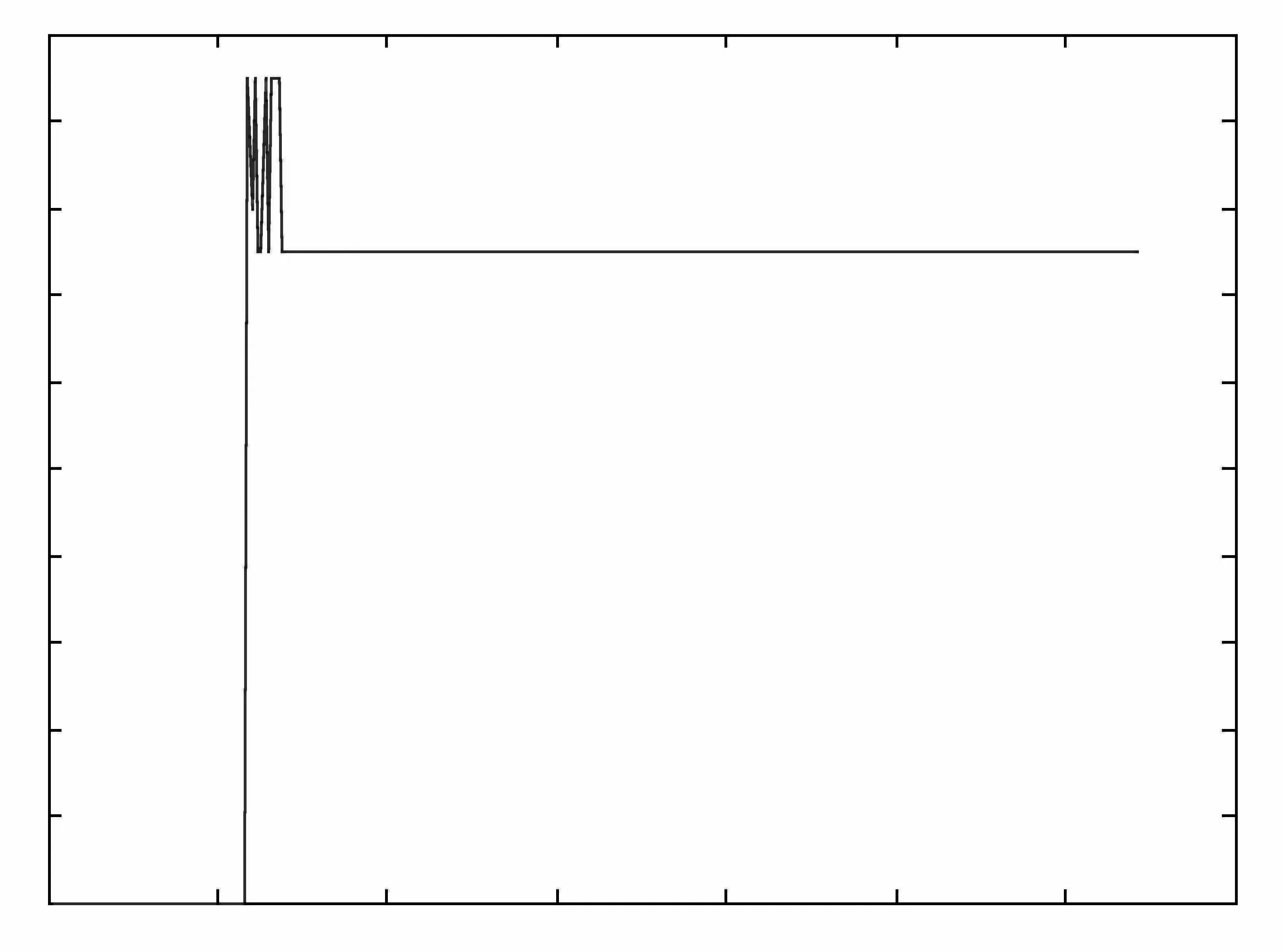
圖2 模糊度N31在每一歷元的固定結果Fig.2 FixedambiguityN31 ineachepoch

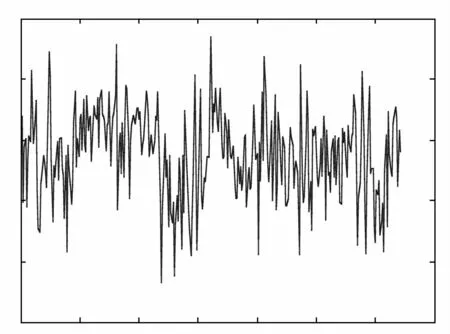
圖3 基線長度Fig.3 Baselinelength

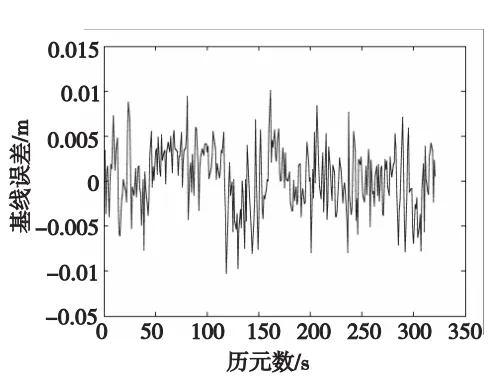
圖4 基線長度誤差Fig.4 Baselinelengtherror

3.4 結果分析

從圖1中可以看出，當用解耦法推算到大概第70個歷元時，模糊度N31的浮點解已經開始逼近真值，并且之后的推算較為平穩；結合表1，由表2和圖2可知，從第69個歷元開始，在動態情況下的每一歷元均能準確固定住模糊度N31，該方法首次固定模糊度用時相比于基于模糊度逼近的搜索法用時更少的原因，是因為后者對模糊度浮點解的精度要求更高，其模糊度解算時間主要消耗于浮點解逼近真值的過程；而本文將解耦法與LAMBDA方法相結合，LAMBDA方法對浮點解的精度要求不如基于模糊度逼近的搜索法苛刻，因而節省了浮點解的求解時間；由圖3和圖4可知，利用解算得到的模糊度反解所得基線長度與實驗前測量結果基本一致，基線長度誤差為1 cm。

4 結論

本文在分析動對動與靜態相對定位中整周模糊度初始化的區別與聯系的基礎上，提出了基于解耦消參的動對動相對定位算法。該算法將基線參量用雙差模糊度參量代替，僅對模糊度浮點解及其協方差矩陣進行實時推算，然后利用LAMBDA算法進行模糊度整數解的搜索與固定。試驗表明，基于解耦消參的動對動相對定位算法初始化模糊度用時較短，在70 s左右即可正確解算出動態單頻整周模糊度，獲得了厘米級的相對定位結果，能夠較好地適用于短基線高精度動態相對定位。

［1］Jacek Paziewski，Pawel Wielgosz.Assessment of GPS+Galileo and multi-frequency Galileo single-epoch precise positioning with network corrections［J］.GPS Solution，2014，18（4）：571-579.

［2］王德軍，熊永良，劉寧，等.寬巷組合及軌跡約束下的列車在軌動態單歷元定位算法［J］.測繪學報，2014，43（2）：131-136.

［3］Wang Bo，Miao Lingiuan，Wang Shunting.A constrained LAMBDA method for GPS attitude determination［J］. GPSSolution，2009（13）：97-107.

［4］段榮，趙修斌，龐春雷，等.改進的GPS整周模糊度動態快速解算［J］.華中科技大學學報（自然科學版），2014，42（9）：54-58.

［5］邱蕾，花向紅，蔡華，等.GPS短基線整周模糊度的直接解法［J］.武漢大學學報（信息科學版），2009，34（1）：97-99.

［6］俞文伯，高國江，趙剡.單頻GPS動態相對定位的模糊度逼近/搜索解法［J］.北京航空航天大學學報，2002，28（2）：242-244.

［7］龐春雷，趙修斌，盧艷娥，等.一種改進型的GPS單頻整周模糊度快速解算方法［J］.兵工學報，2012，33（11）：1387-1392.

［8］Chen Wantong，Qin Honglei.New method for single epoch，single frequency land vehicle attitude determination using low-end GPS receiver［J］.GPS Solution，2012，（16）：329-338.

［9］劉志儉.GPS載波相位差分技術、捷聯慣性導航系統初始對準技術及其組合技術研究［D］.長沙：國防科學技術大學，2003.

［10］Teunissen PJG.The least-squares ambiguity decorrelation adiustment：a method for fast GPSinteger ambiguity estimation［J］.Journal of Geodesy，1995（70）：65-82.

Dynamic Relative Positioning Algorithm Based on Decoupling Parameter Elimination

WU Shaoshi，ZHAO Xiubin，PANG Chunlei，YU Yonglin，LIU Ming
（Information and Navigation College，Air Force Engineering University，Xi’an 710077，China）

It is difficult to obtain the integer ambiguity precisely because baseline is real-time changeable in dynamic to dynamic relative positioning，.On the basis of comparison between dynamic to dynamic relative positioning and static relative positioning，an algorithm for dynamic to dynamic relative positioning based on parameter elimination with decoupling method was proposed.The algorithm combined the decoupling method and LAMBDA algorithm.Firstly，double difference carrier phase observation equations were transformed through decoupling method，so that the baseline parameters were removed and the float solution and its covariance matrix of double difference of integer ambiguity were deduced in real-time，then integer ambiguities were fixed and confirmed by LAMBDA algorithm.The test revealed that it took only seventy seconds to calculate the single tone dynamic ambiguity with the proposed algorithm and the baseline error being cm-level，which meant that the proposed algorithm was suitable for short-baseline dynamic scenarios with high-precision.

dynamic to dynamic；relative positioning；integer ambiguity；decoupling；LAMBDA

TN967.1

A

1008-1194（2015）05-0026-04

2015-05-25

國家自然科學基金資助項目（61273049）

伍劭實（1990—），男，湖北宜昌人，碩士研究生，研究方向：衛星導航與定位。E-mail：wushaoshipaper@ 163.com。