155 mm口徑火炮榴彈結構特征數分布特性研究
王曉鵬,王雨時,盧鳳生,聞 泉,劉錦春
(1南京理工大學機械工程學院,江蘇南京210094;2黑龍江華安機械有限責任公司,黑龍江齊齊哈爾161046)
155 mm口徑火炮榴彈結構特征數分布特性研究
王曉鵬1,王雨時1,盧鳳生2,聞 泉1,劉錦春2
(1南京理工大學機械工程學院,江蘇南京210094;2黑龍江華安機械有限責任公司,黑龍江齊齊哈爾161046)
彈丸的結構特征數直接影響彈丸外彈道飛行運動,而結構特征數極限值影響引信在外彈道的極限力學環境。針對工程中難以得到彈丸結構特征數極限值,提出利用榴彈結構特征數實測數據擬合其數學分布并進一步研究其分布特性的方法。155 mm榴彈結構特征數中,質量和質心軸向位置同時服從正態分布和Weibull分布,赤道轉動慣量服從Weibull分布;為改善射擊密集度對彈體部分尺寸公差加嚴后,極轉動慣量同時服從正態分布和Weibull分布,質量服從Weibull分布。尺寸公差加嚴后除質心位置外的其余結構特征數散布均變小。偏心距極小值為零,極大值為0.35 mm。
引信設計;結構特征數;數理統計;彈道環境
0 引言
彈丸的結構特征數(主要包括彈丸質量、軸向質心位置、極轉動慣量、赤道轉動慣量和偏心距),直接影響彈丸的外彈道飛行運動。文獻[1]的研究表明由于砂彈的質心位置和極轉動慣量散布直接影響彈丸動力平衡角,進而造成了彈丸射擊精度差。另外彈丸動力平衡角可以看做是彈丸的平均章動角[2],對于旋轉彈而言引信受到的章動力與彈丸最大章動角成正比[3],因此在計算引信外彈道所受章動力時應充分考慮彈丸結構特征數的散布和極限值影響。
但在彈丸生產過程中往往并不對這些參數進行直接檢測和控制,而是通過檢測彈丸的其他參數來間接保證的。例如,對于彈丸偏心距的控制主要是通過檢測并控制彈體壁厚差來間接保證的。在早期彈丸設計中彈丸結構特征數可采用基本計算法或其改進算法通過人工計算或編程計算得出[4-9]。隨著計算機技術的快速發展,利用計算機三維設計軟件就可以實現對彈丸結構特征數的便捷計算[10]。但這些方法都是按照名義尺寸或平均尺寸進行的計算,只能得到名義值或近似平均值,難以得到散布情況和極限值。
文獻[11]研究了某82 mm迫擊炮彈結構特征數的分布規律,目前尚未見有關于榴彈結構特征數分布規律的研究文獻。相比于迫擊炮彈,榴彈速度大、射程遠、射擊密集度要求高,引信外彈道力學環境更復雜也更惡劣,因此研究榴彈結構特征數的數學分布對于研究它們對彈丸外彈道飛行運動特別是引信設計所關注的極限彈道環境的影響意義更大。本文針對此問題,根據155 mm口徑火炮殺傷爆破彈結構特征數實測數據,運用數理統計方法擬合其數學分布,并進一步研究其分布特性。另外,對比分析了彈體部分尺寸公差加嚴對彈丸結構特征數分布的影響。
1 樣本概述
現有155 mm口徑火炮榴彈結構特征數實測數據217組。為改善射擊精度,對彈體上的部分尺寸公差進行了加嚴控制,見表1。加嚴控制后的榴彈結構特征數實測數據277組。這兩種情況下的樣本極值如表2所列。其中質量、質心和偏心距數值由PGE-100型綜合測試儀測量得出。

表1 彈體部分尺寸公差和粗糙度加嚴情況Tab.1 The dimensional tolerances and roughness tightened conditions of proiectiles
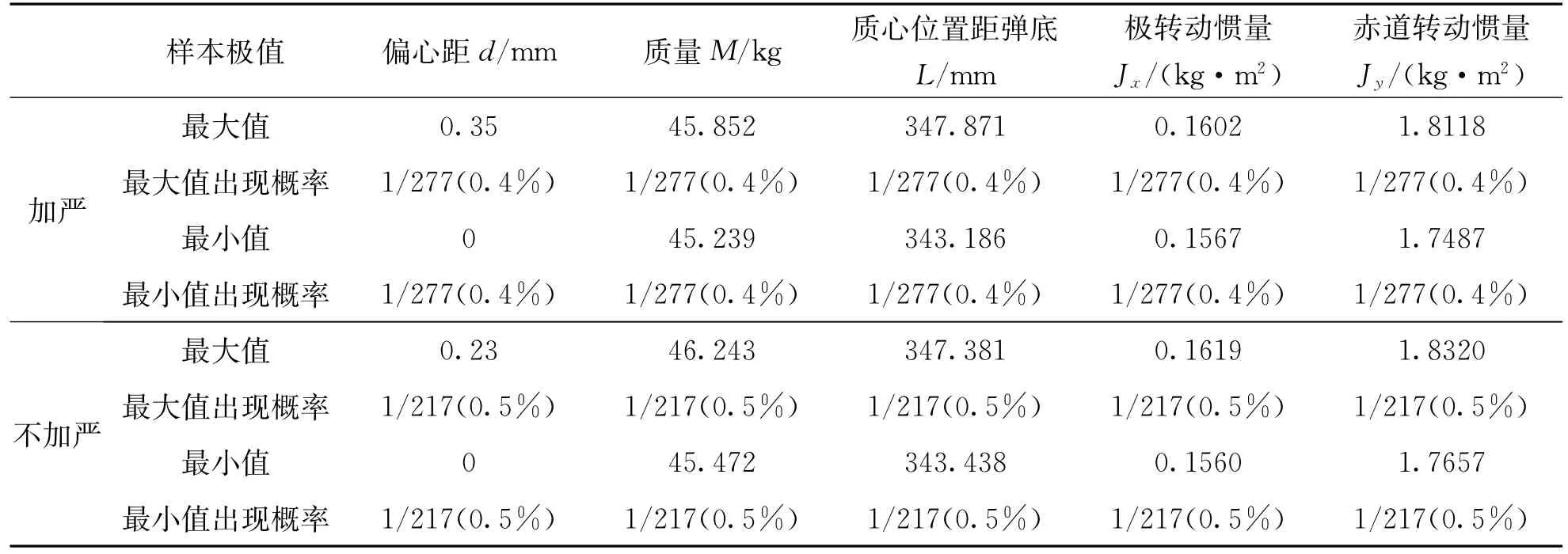
表2 實測數據樣本極值Tab.2 Extreme values of measured data sample
2 分布假設、參數估計和分布擬合檢驗
繪制加嚴控制和不加嚴控制樣本數據統計直方圖分別如圖1和圖2所示。假設各參數服從正態分布,加嚴控制和不加嚴控制實測數據估計的正態分布參數如表3所列。
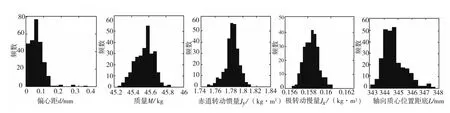
圖1 加嚴控制榴彈結構特征數樣本數據統計直方圖Fig.1 The statistical histogram of proiectiles’structural characteristics several sample parameters in tightened contro

圖2 不加嚴控制榴彈結構特征數樣本數據統計直方圖Fig.2 The statistical histogram of proiectiles’structural characteristics parameters sample parameters in non-tightened control
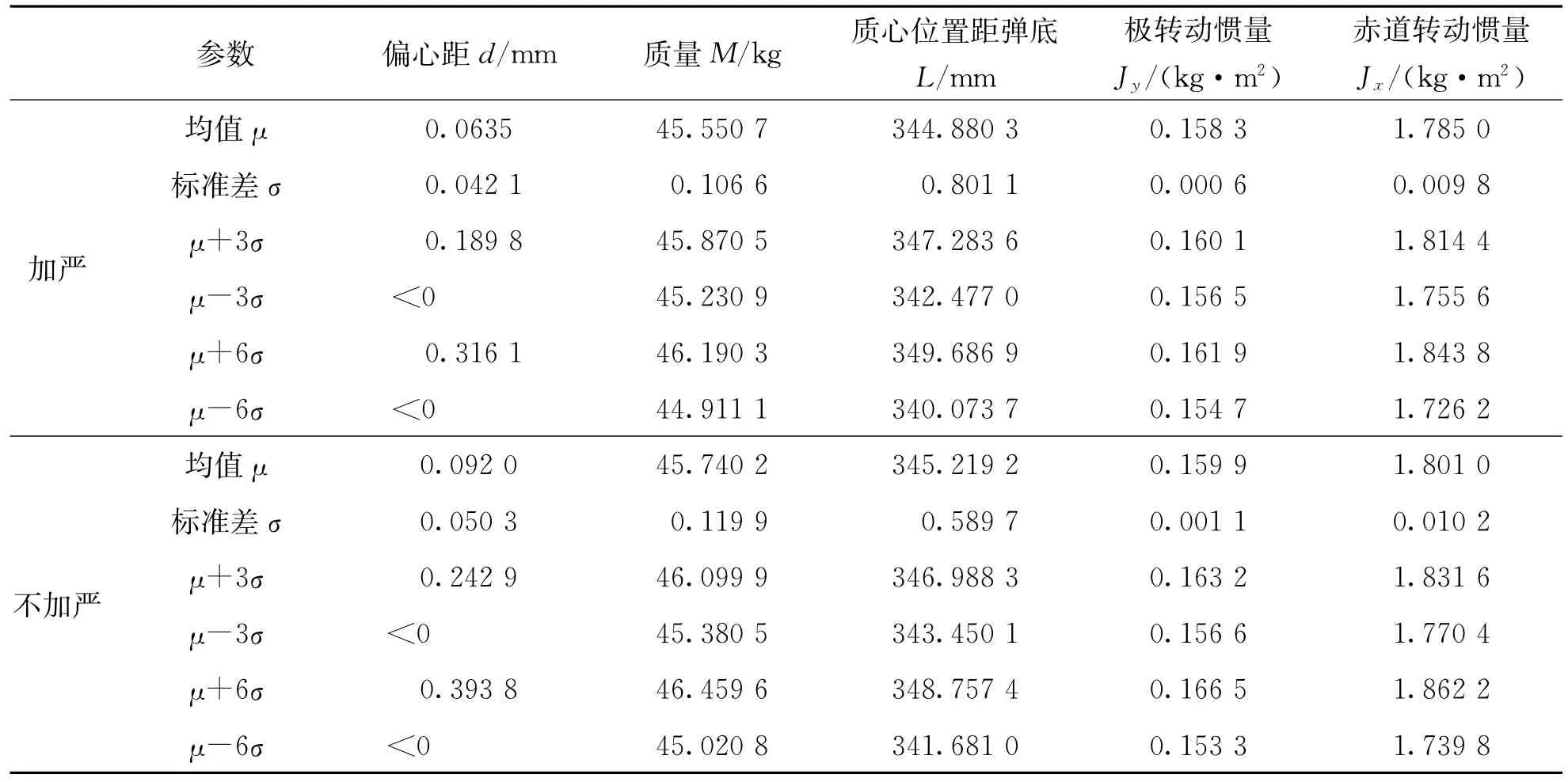
表3 各參數正態分布參數估計值Tab.3 The parameter estimates of normally distributed for proiectiles’structural characteristics parameters
對上述分布假設利用皮爾遜的χ2檢驗方法進行分布擬合檢驗,若檢驗統計量檢驗滿足χ2<(k —r—1),則接受假設。檢驗結果分別如表4所列。
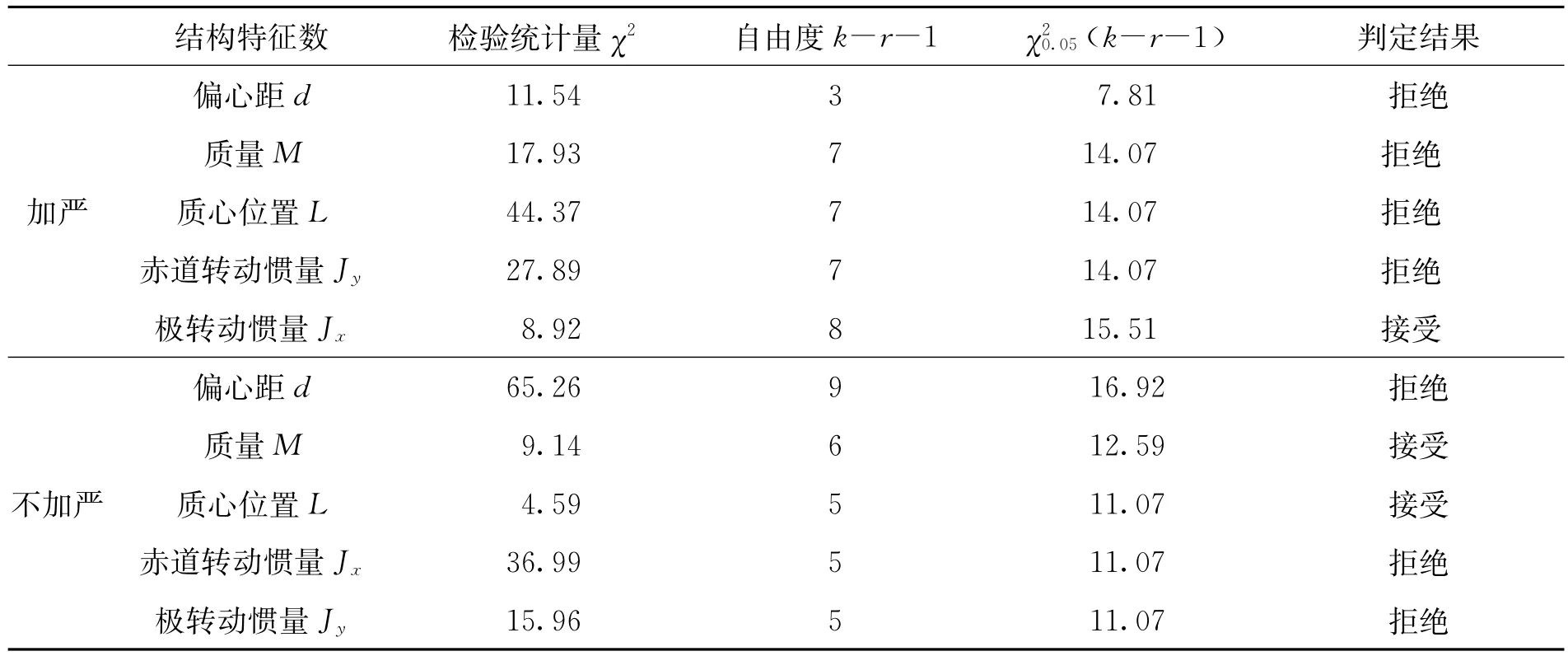
表4 各結構特征數正態分布χ2檢驗結果Tab.4 Theχ2 test results for normally distributed of proiectiles’structural characteristics parameters
由表4可以看出,加嚴控制的榴彈結構特征數中只有極轉動慣量服從假設的正態分布,不加嚴控制的榴彈結構特征數中質量和質心位置服從假設的正態分布。
除正態分布外,三參數Weibull分布也是一種靈活性強、應用廣泛的分布類型,假設榴彈的結構特征數服從三參數Weibull分布,采取加嚴質量控制和不采取加嚴質量控制的榴彈結構特征數其三參數Weibull分布參數的極大似然估計值分別如表5所列。
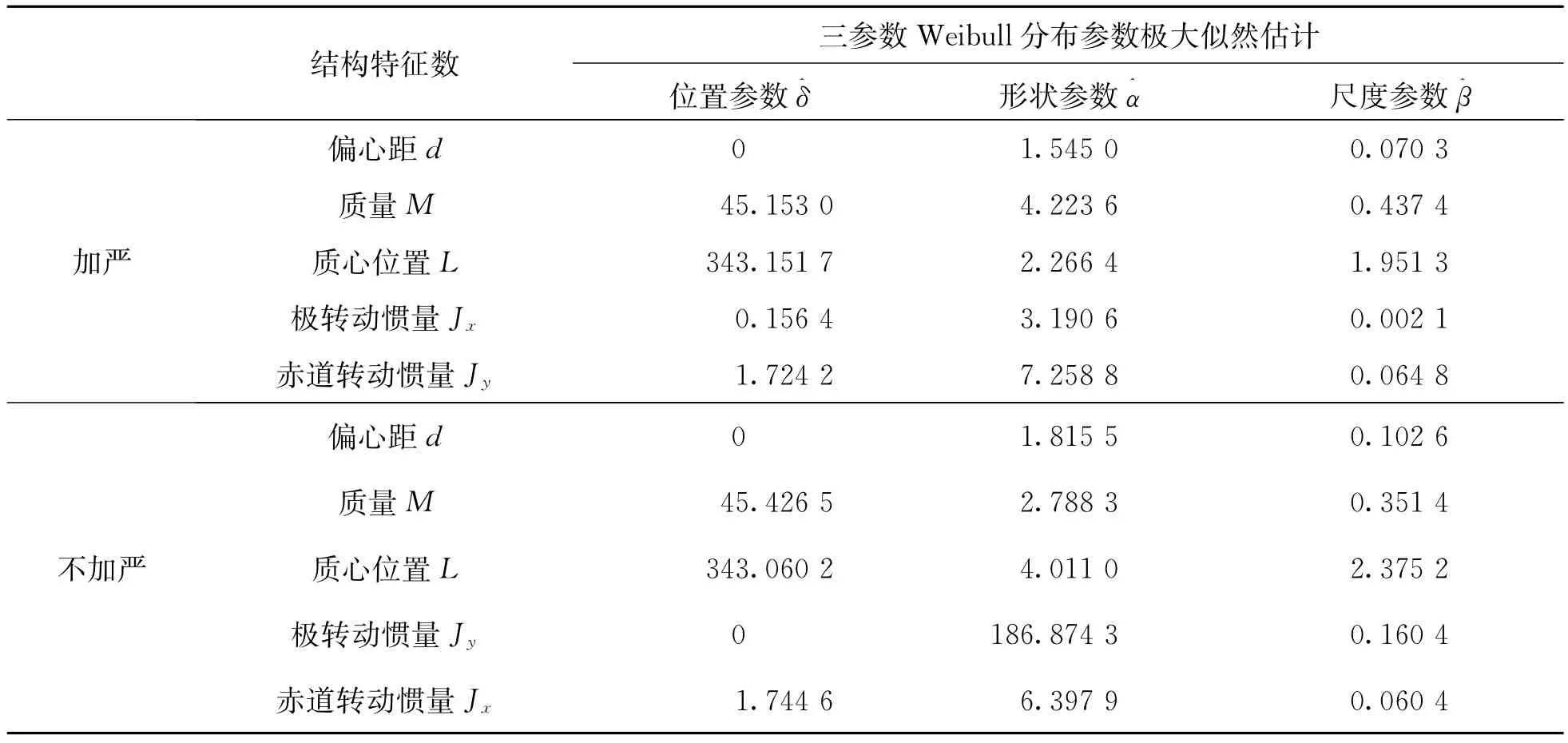
表5 榴彈各參數三參數Weibull分布參數極大似然估計值Tab.5 The maximum likelihood estimates of the three-parameter Weibull distribution parameters of proiectiles’structural characteristics parameters
對上述分布假設利用皮爾遜的χ2檢驗方法進行分布擬合檢驗,檢驗結果如表6所列。
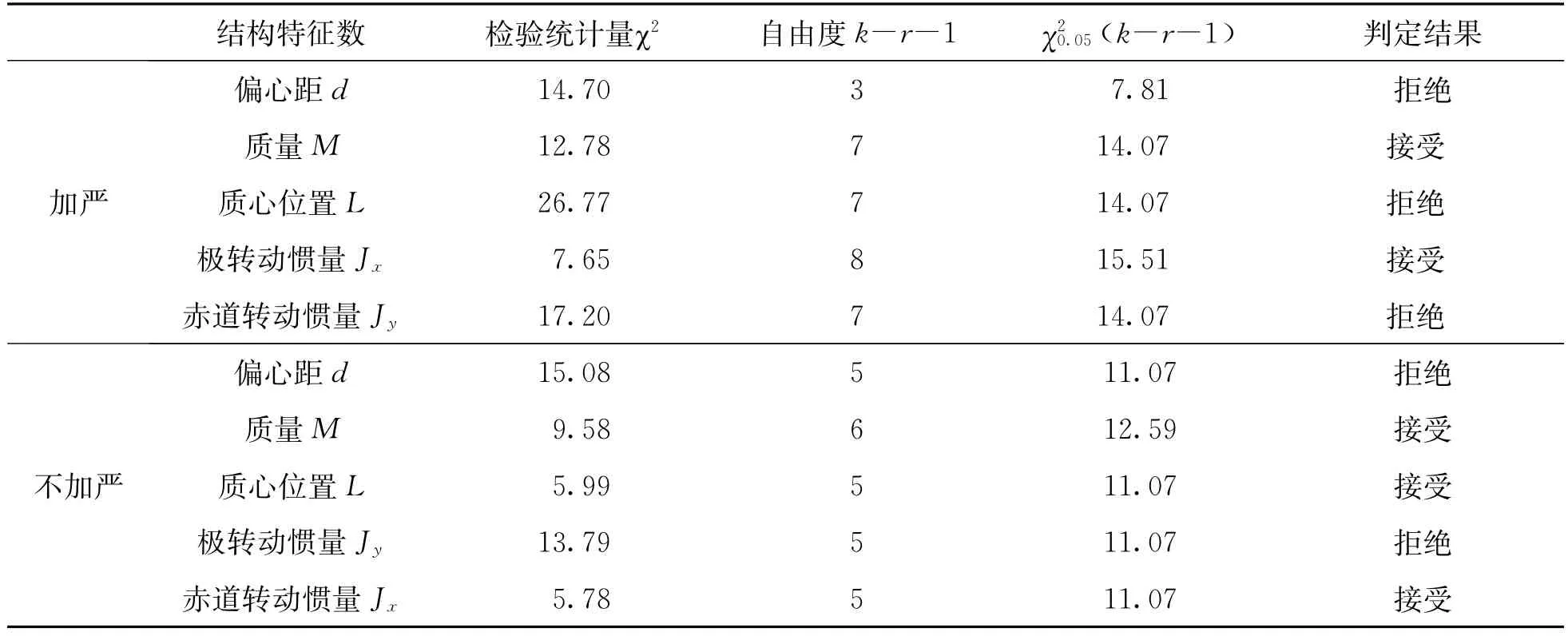
表6 榴彈各結構特征數三參數Weibull分布χ2檢驗結果Tab.6 Theχ2 test results for three-parameter Weibull distribution of proiectiles’structural characteristics parameters
由表6可以看出,加嚴控制榴彈的結構特征數中質量和極轉動慣量服從假設的三參數Weibull分布,不加嚴控制榴彈的結構特征數中質量、質心位置和赤道轉動慣量服從假設的三參數Weibull分布。
3 分析和討論
通過計算實測數據均值和方差來驗證分布類型的準確性,其中Weibull分布的均值和方差根據式(1)計算,兩組數據計算結果及相對誤差分別如表7所列。
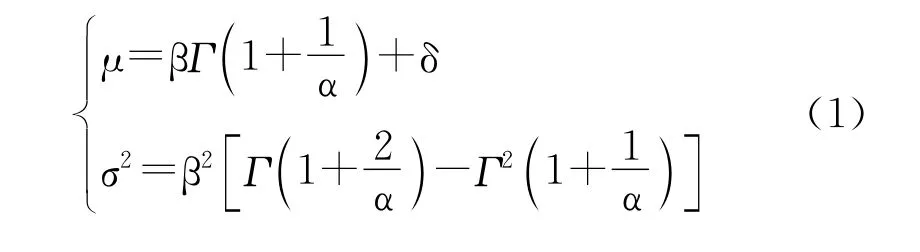
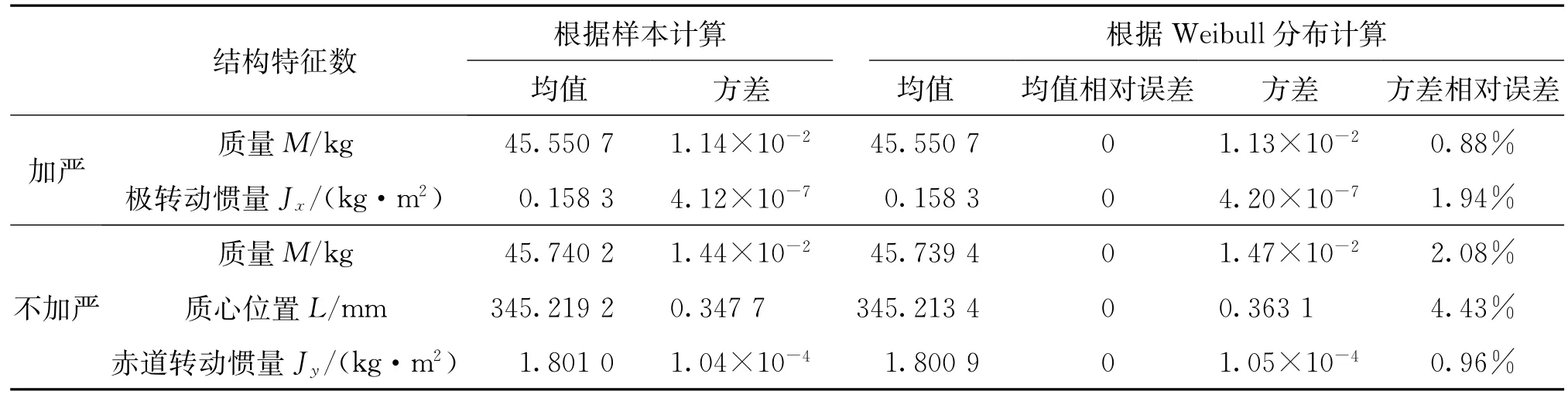
表7 根據Weibull分布計算得各參數均值和方差及相對誤差Tab.7 The relatives error of mean and variance of each parameter according to Weibull distribution
由表7可以看出,兩組數據根據三參數Weibull分布計算得到的各參數均值和方差與樣本實際情況吻合得很好,均值計算結果取四位小數與樣本無相對誤差,方差相對誤差不超過3%。
加嚴控制數據的質量與極轉動慣量以及不加嚴控制數據的質量、質心位置與極轉動慣量按Weibull分布概率計算得極值區間如表8和表9所列。其中4‰和5‰的選取分別與表2中兩種情況的樣本極值概率相對應。

表8 加嚴控制數據按Weibull分布概率計算得極值區間Tab.8 The extreme interval of tightened control data calculated by the Weibull distribution probability

表9 不加嚴控制數據按Weibull分布概率計算得極值區間Tab.9 The extreme interval of non-tightened control data calculated by the Weibull distribution probability
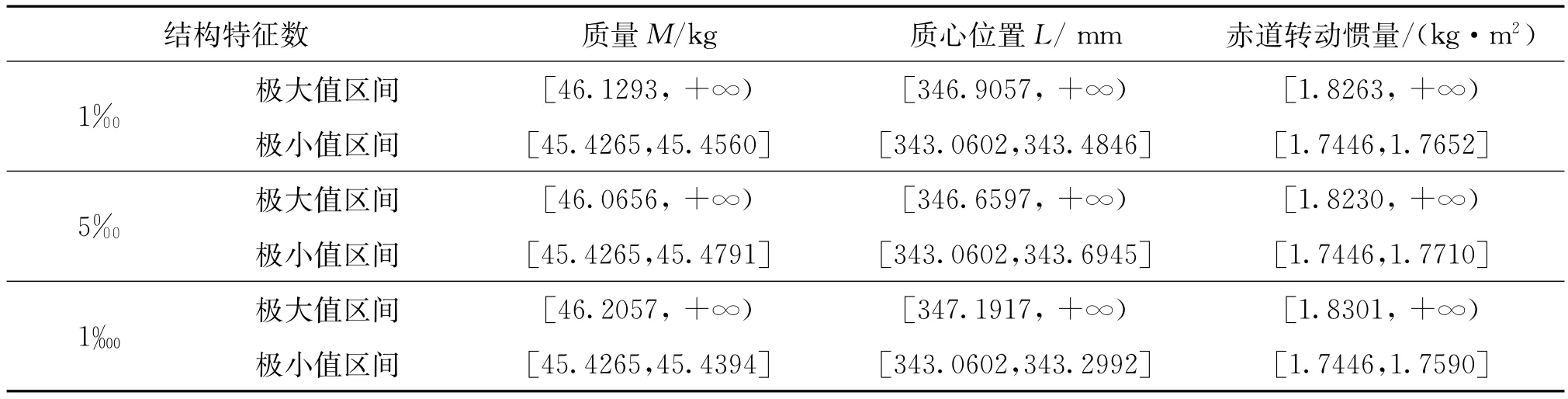
續表
對比表8表、表9和表2可得,樣本實測數據極值與按Weibull分布概率計算得到的極值區間基本吻合。
計算各參數間不相關假設檢驗概率P,加嚴控制和不加嚴控制的榴彈結構特征數計算結果分別如表10和表11所列。通常認為P<0.05時,兩個隨機變量相關性顯著。
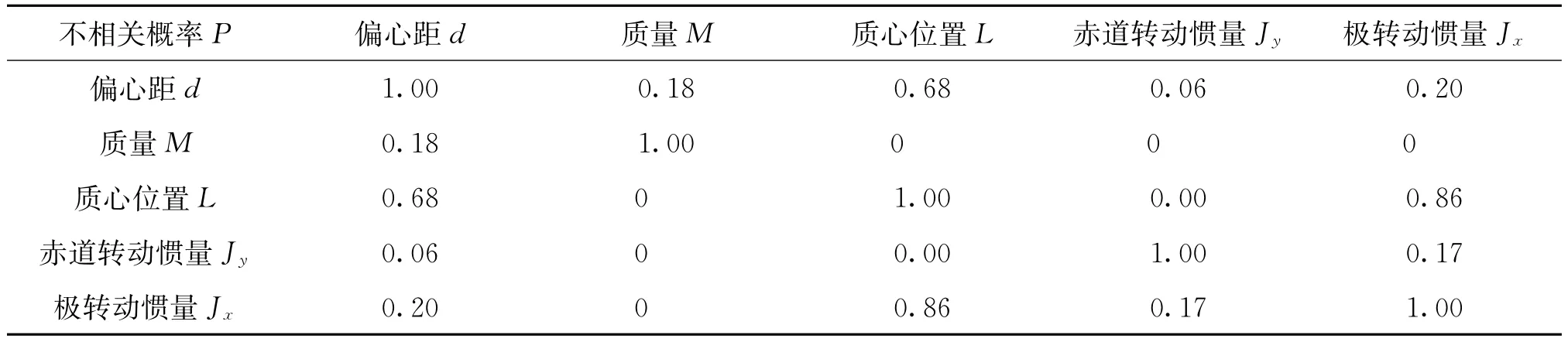
表10 加嚴控制的榴彈各參數間不相關假設檢驗概率PTab.10 The not relevant hypothesis testing probability P among tightened control data

表11 不加嚴控制的榴彈各參數間不相關假設檢驗概率PTab.11 The not relevant hypothesis testing probability P among non-tightened control data
由表10可以看出,加嚴控制的榴彈結構特征數中質量與質心位置、赤道轉動慣量和極轉動慣量三個變量的相關性顯著。質量與赤道轉動慣量和極轉動慣量相關性顯著,這與轉動慣量的定義相吻合。質量與質心位置相關性顯著,可能是彈丸沿軸向的某一部分起決定性作用。還可以發現,偏心距與赤道轉動慣量和極轉動慣量的相關性不顯著,這與轉動慣量的定義不一致。此外傳統認為偏心距應服從Weibull分布的特例Rayleigh分布,但在此不滿足。這些都在一定程度上說明偏心距的測量數據可能因有效數字位數太少而使其分布特性出現較大偏差。由表11可以發現,不加嚴控制的榴彈結構特征數之間的相關性除了包括加嚴控制的榴彈結構特征數之間的相關性以外,偏心距和質量、質心位置之間也表現出顯著相關性。
4 結論
根據155 mm口徑火炮榴彈結構特征數實測數據,經分布假設、參數估計和假設檢驗得出:對彈體部分尺寸公差加嚴控制時彈丸的極轉動慣量服從正態分布,質量和極轉動慣量服從三參數Weibull分布;不加嚴控制時彈丸的質量和質心位置服從正態分布,質量、質心位置和赤道轉動慣量服從三參數Weibull分布。且樣本實測均值和方差與按三參數Weibull分布計算得均值和方差吻合很好,相對誤差不超過3%。
相比于不加嚴控制,采取加嚴控制后有如下效果:質心位置(距彈底)由于對彈體上定心部距彈口尺寸公差的加嚴、上定心部向彈口前移而導致彈丸質心位置(距彈底)變大;偏心距未隨加嚴控制而加嚴,加嚴控制后最大值為0.35 mm,大于不加嚴控制時的最大值0.23 mm;其余結構特征數均值都隨加嚴控制而變小;除質心位置以外其余各結構特征數散布均變小。
不論是否采取加嚴控制,彈丸偏心距最小值都是0,這在引信設計時應引起特殊關注。
另外,研究發現榴彈不可避免的存在偏心,必定導致彈丸自轉的不對稱性,增大旋轉彈丸極阻尼力矩,影響彈丸轉速衰減和穩定性,在設計時應予以考慮。此外,對于引信中的滑塊等偏心運動件,在設計啟動偏心時應考慮彈丸偏心距極大值的影響。
[1]孫浩,金建峰,王兆波.改裝彈丸特征量對射彈散布的影響分析[J].彈箭與制導學報,2014,34(4):93-96.
[2]浦發.外彈道學(中冊)·火炮彈丸的飛行穩定性理論[M].北京:國防工業出版社,1964.
[3]李占雄,郭占海,王叔來,等.GJB/Z 135-2002引信工程設計手冊[S].北京:總裝備部軍標出版發行部,2002.
[4]華恭,歐林爾.彈丸作用和設計理論[M].北京:國防工業出版社,1975.
[5]魏惠之.計算彈丸結構特征數的兩種新方法[J].兵工學報(彈箭分冊),1981(4):1-8.
[6]孫瑞書,譚鳳翔.計算彈丸特征量的普遍公式[J].兵工學報,1983(1):60-64.
[7]吳子明.平截正圓錐法——計算彈丸結構特征數方法[J].兵工學報(彈箭分冊),1984(4):53-62.
[8]王曉鳴.彈丸結構特征數三維計算方法[J].兵工學報(彈箭分冊),1990(3):57-63.
[9]黃德武,谷耀新.用等參元方法計算彈丸結構特征數[J].沈陽工業學院學報,1990,9(3):27-34.
[10]張元軍.彈丸結構特征數的計算方法[J].四川兵工學報,2008,29(4):47-48.
[11]王曉鵬,王雨時,聞泉,等.某82 mm迫彈力學參數分布特性研究[J].彈箭與制導學報,2014,34(4):73-77.
Distribution Characteristics of 155 mm Caliber Projectile’s Structural Characteristics Parameters
WANG Xiaopeng1,WANG Yushi1,LU Fengsheng2,WEN Quan1,LIU Jinchun2
(1.School of Mechanical Engineering,Naniing University of Science and Technology,Jiangsu,Naniing 210094,China;2.Heilongiiang Huaan Machine Corporation LTD,Qiqihaer 161046,China)
The external ballistics was influenced by the proiectile structural characteristics parameters,and the limit ballistic environment can’t be calculated accurately.A method of fitting and researching mathematical distribution of proiectile’s structural characteristics parameters according to the measured data was proposed in this paper.A 155 mm caliber proiectile’s axial centric position and mass obeyed normal distribution and Weibull distribution,moment of inertia of the equator obeyed Weibull distribution.To improve shot—intensive,part of the dimensional tolerances on proiectile were tightened,then the proiectile’s polar moment of inertia obeyed normal distribution and weibull distribution,mass obeys weibull distribution.
ammunition engineering;structural characteristics parameters;mathematical statistics;traiectory environment
TJ430
A
1008-1194(2015)05-0066-07
2015-03-03
王曉鵬(1989—),男,河北張家口人,碩士研究生,研究方向:探測制導與控制。E-mail:xpwang1989@163.com。

