改進的復值快速獨立分量分析算法

尹洪偉，李國林，路翠華

（海軍航空工程學院，山東煙臺264001）

改進的復值快速獨立分量分析算法

尹洪偉，李國林，路翠華

（海軍航空工程學院，山東煙臺264001）

針對復值快速獨立分量分析算法（CFastICA）對初始權值敏感且收斂速度較慢的問題，提出了改進的CFastICA算法。該算法首先利用牛頓下降因子優化牛頓迭代的收斂方向，使分離矩陣在一定程度上接近最優值，然后去除牛頓收斂因子，利用普通牛頓迭代實現分離矩陣快速收斂。仿真實驗表明：提出的算法擁有和牛頓下降CFastICA同樣的收斂精度，收斂時間比牛頓下降CFastICA減少了近53%，且在低SNR下，提出算法的綜合收斂性能明顯優于CFastICA和牛頓下降CFastICA算法。

盲源分離；復值快速獨立分量分析算法；牛頓迭代

0 引言

由于盲分離算法對信號先驗知識無依賴性，近年來其在雷達、聲吶、語音、通信、圖像和醫學等領域都得到了快速發展［1-2］。而一些領域，如陣列信號處理，其信號往往是復數形式，針對該特點，實數盲分離算法被擴展到了復數領域［3］。其中最典型的算法為復值快速獨立分量分析（FastICA）算法，該算法因采用牛頓迭代而具有較快的收斂速度。但該算法存在一個大的缺陷，即當初始分離矩陣偏離最優值較遠時，特別是含噪聲條件下，不容易收斂到到最優點，甚至無法收斂［4-5］。為解決這個問題，國內外不少學者進行了研究。但總體來看，對該問題的解決方法主要有三種：一是對算法中非線性函數的優化，如文獻［6—8］，該方法雖可以在一定程度上緩解上述問題，但是也只是起到改善的效果，并不能從根源上解決；二是引入牛頓下降因子以保證牛頓迭代朝著最優值方向，如文獻［9—11］，雖然效果很好，但這使得本來具有快速收斂優勢的牛頓算法速度被削減；三是先利用最速梯度法改善初始分離矩陣，然后再利用牛頓迭代獲取最優分離矩陣，如文獻［5，12］，但是該算法中的所謂最速梯度，實際上就是牛頓算法［12］，并不能起到良好的穩定效果。本文針對此問題，提出了改進的CFastICA算法。

1 復值ICA原理與信號預處理

1.1 復值ICA原理

早在20世紀60年代，Darmois就提出：若果源信號是相互獨立的，那么通過恢復混合后信號之間的相互獨立性就可得到源信號的估計［13］。

根據上述原理，假設有N個源信號s1（t），s2（t），…，sN（t），信號在接收端瞬時線性混合，則接收信號可表示為

式中：X=［x1，x2，…，xm］T為接收信號矩陣；S=［s1，s2，…，sN］T為源信號矩陣；A?Cm×N（m≥N）為信號混合矩陣；n=［n1，n2，…，nm］T為觀測白噪聲，且ni的方差為σ2并與源信號相互獨立。

盲分離就是尋找一個代價函數J（W ），并通過某種優化準則使J（W ）達到最優值，此時的W即為所需分離矩陣，源信號的估計可以表示為

式中：y=［y1，y2，…，yN］T為源信號的估計。但是通常分離信號與源信號在幅值和順序上有所區別。

1.2 信號白化預處理

白化預處理是盲分離前十分重要的一步，它不僅可以改善盲分離算法的穩定性，還可對接收信號進行降維（當m≥N時）以減少計算量。

白化處理過程如下，設接收信號X已去均值，則其自相關矩陣可表示為

對RX特征值分解，可得

式中：U=［u1，u2，…，um］T為特征向量矩陣；Λ= diag｛［λ1，λ2，…，λm］｝為特征值矩陣。

當m=N時，白化矩陣為

當m＞N時，需對信號降維，假設特征值λ1≥λ2≥…≥λm，若能獲取信號個數N，則白化矩陣可以表示如下

式中：US=［u1，u2，…，uN］T為信號子空間向量矩陣；ΛS=diag｛［λ1，λ2，…，λN］｝為其對應的特征值矩陣。而源信號數目的估計可以通過MDL，AIC等算法獲取［14］。

于是，白化后信號為

2 CFastICA算法

CFastICA算法是FastICA算法引入到復值領域的擴展形式，其代價函數為

式中：W=［w1，w2，…，wn］T為復數分離矩陣；G為非線性函數；Z為白化后的信號矩陣。

在復值盲分離中通常假設分離信號幅值為1，等價于在E｛WZ2｝=WHW=I下最優化代價函數，于是式（8）可寫為

利用牛頓算法對式（9）進行優化，可以得到分離矩陣W的迭代公式

式中：g為G的導數；g'為g的導數。非線性函數的選擇通常有以下三種：

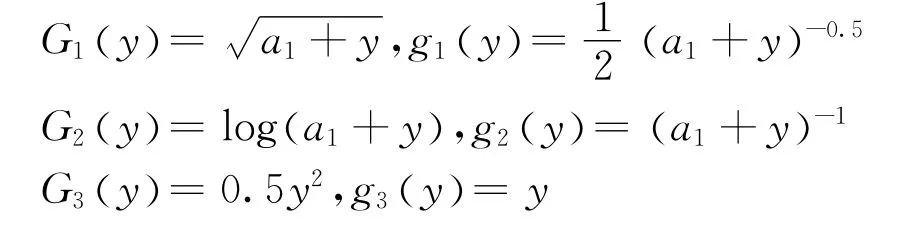
3 改進的CFastICA算法

為改善算法對初始矩陣的敏感性，引入牛頓下降法，在迭代公式（3）中加入牛頓下降因子，可得

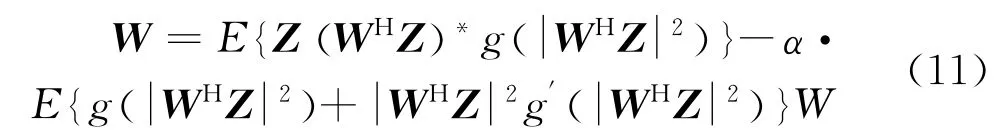
式中：0＜α＜1為牛頓下降因子。

在式（10）和（11）的迭代公式中利用了白化信號特性E（ Z ZH）=I，但是當m＞N時，由1.2節分析可知

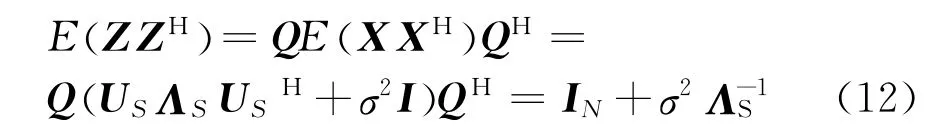
由此，可見E（ Z ZH）≠I，特別是SNR較低時更為明顯。于是，對式（11）修正，可得

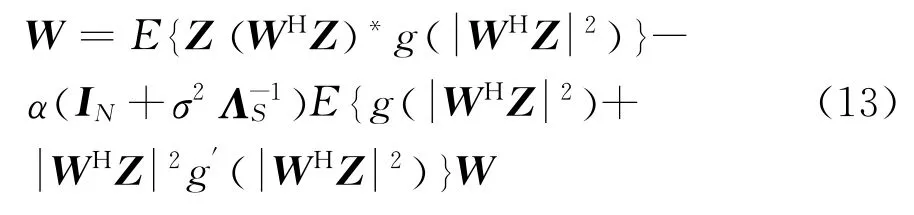
引入牛頓下降法雖提高了收斂穩定性，卻降低了算法的收斂速度，為改善該缺陷，本文提出在信號分離初期利用牛頓下降法進行分離，當分離矩陣達一定精度之后，轉為普通CFastICA算法，這樣既能保證算法的穩定性，又能提高收斂速度。

改進后的算法步驟如下：

1）對接收信號X預處理，得到白化信號Z；

2）設置初始收斂因子0＜ε?1，0＜δ＜ε和初始分離矩陣W0；

3）利用式（13）迭代獲取分離矩陣W；

4）判斷分離矩陣是否滿足W—Wlast≤ε（Wlast為迭代前分離矩陣），若不滿足，返回步驟3）；

5）利用去掉牛頓下降因子α的式（13）進一步迭代，獲取分離矩陣W；

6）判斷分離矩陣是否滿足W—Wlast≤δ，若不滿足，返回步驟5）；

7）獲取分離信號y=WZ。

4 實驗仿真與分析

為驗證算法有效性，選取3個源信號，圖1給出了信號的局部視圖，其中信號1為頻率1 MHz的余弦信號，信號2為調頻率等于4×1011Hz/s的LFM信號；信號3為頻率2.5 MHz的正弦信號。仿真信號采樣點數為5 000，仿真時信號采用復數形式，計算機主頻2.1 GHz。

混合矩陣A利用Matlab隨機產生，經混合后的信號形式如圖2所示。由圖可以看出，接收信號是雜亂無章的，無法辨析源信號。為此，需要對信號進行分離。

利用改進的CFastICA算法分離后的波形如圖3所示，可見混合信號經盲分離后，波形得到了很好的恢復，只是信號的順序和幅度與源信號略有差異。

圖1 源信號波形Fig.1 Waves of source signals

圖2 接收信號波形Fig.2 Waves of received signals

圖3 分離信號波形Fig.3 Waves of separated signals

為說明本文算法的分離性能，首先給出收斂性能指數PI的定義

式中：gij為全局矩陣［15］G中的元素；maxjgij為G中第i行元素中模的最大值；maxjgji為第j列元素中模最大值，且PI值越小，分離性能越好。

實驗設置牛頓下降因子α=0.2，每種算法的初始分離矩陣均相同。圖4給出了SNR=5 dB時CFastICA算法、牛頓下降CFastICA算法和本文算法的收斂速度對比。

從圖4中可以看出，當初始分離矩陣不理想且噪聲較大時，牛頓下降法收斂速度緩慢，CFastICA算法雖收斂速度很快，但不能收斂到最優值，而本文算法在初始階段因采用牛頓下降法而收斂較慢，當達到一定收斂性能時，改用牛頓迭代而迅速收斂，改進的算法既保證了快速收斂，同時又具有與牛頓下降CFastICA算法同樣的收斂性能。

進一步提高信噪比，圖5在SNR=25 dB時給出了算法的收斂性能，可以看出隨著SNR的提高，牛頓下降法和本文算法收斂速度都有很大提高，且在三種算法收斂性能都提高的同時，本文算法收斂性能同樣優于CFastICA算法。而當接收信號中不含有噪聲時，如圖6所示，3種算法的收斂性能幾乎一致。因此，本文算法在觀測數據含噪聲條件下更具有優勢。

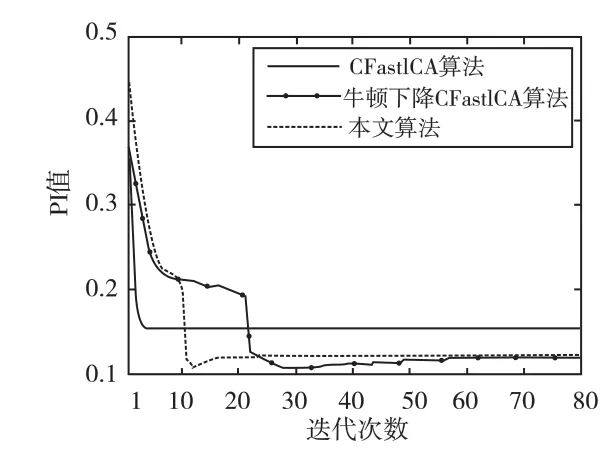
圖4 SNR=5 dB時算法收斂速度Fig.4 Convergence speeds ofthe algorithms when SNR=5 dB

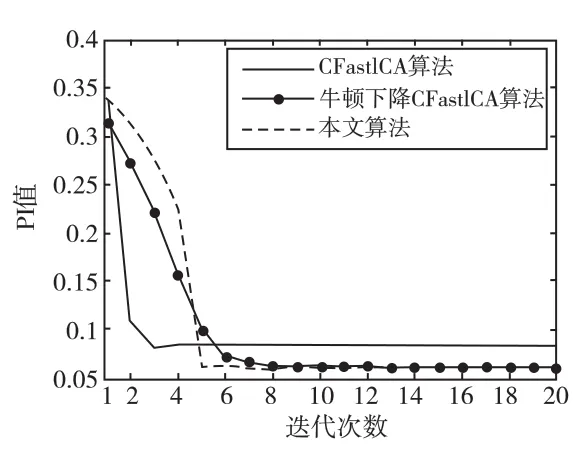
圖5 SNR=25 dB時算法收斂速度Fig.5 Convergence speeds of the algorithms when SNR=25dB

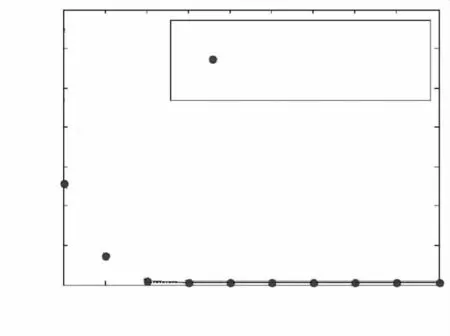
圖6 無噪聲時算法收斂速度Fig.6 Convergence speeds of the algorithms when there’s no noise

從運算時間方面，表1給出了3種算法在SNR =20 dB時對應的分離時間，可以看出CFastICA算法具有最短的運算時間，牛頓下降CFastICA運算時間最長，而本文算法處于兩者之間，其運算時間比CFastICA算法慢40.47%，比牛頓下降CFastICA快52.85%。當無噪聲時，由圖6可知三種運算時間應是相當的，而有噪聲特別是SNR較低時，綜合收斂精度和運算時間來看，本文算法性能較好。

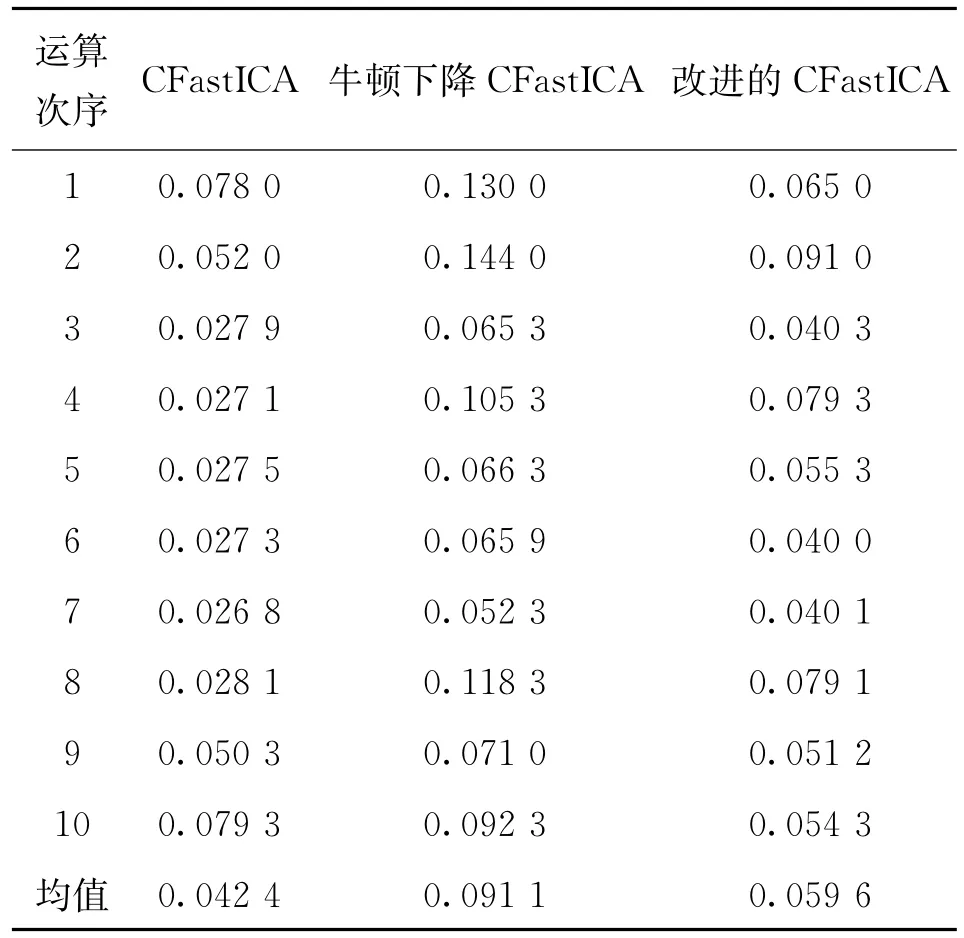
表1 不同算法運算時間對比Tab.1 Time comparison of different algorithms

5 結論

本文提出了改進的CFastICA算法，該算法結合CFastICA算法和牛頓下降CFastICA算法的優點，較好地解決了CFastICA算法的初值敏感和牛頓下降CFastICA算法收斂速度慢的問題。仿真實驗表明，提出的算法在低SNR擁有更好的性能。但算法收斂速度與CFastICA算法還有一定差距，下一步的研究方向應集中在非線性函數方面，通過優化非線性函數來提高收斂速度。

［1］ElRhabi M，Fenniri H，Keziou A，et al.A robust algorithm for convolutive blind source separation in presence of noise［J］.Signal Processing，2013，93：818-827.

［2］Abolghasemi V，Ferdowsi S，Sanei S.Blind separation of image sources via adaptive dictionary learning［J］. IEEE Transactions on Image Processing，2012，21（6）：2921-2930.

［3］Novey M，Adal T.Complex ICA by negentropy maximization［J］.IEEE Transactions on Neural Networks，2008，19（4）：596-609.

［4］孫守宇.盲信號處理基礎及其應用［M］.北京：國防工業出版社，2010：33-34.

［5］季策，胡祥楠，朱麗春，等.改進的高階收斂FastICA算法［J］.東北大學學報（自然科學版），2011，32（10）：1390-1393.

［6］Mehrabian H，Pang I，Chopra R，et al.An adaptive complex independent component analysis to analyze dynamic contrast enhanced-MRI［C］//IEEE International Symposium on Biomedical Imaging（ISBI），2012，9：1052-1055.

［7］趙立權，于軾群.改進的快速復值FastICA算法研究［J］.東北電力大學學報，2012，32（2）：87-91.

［8］Chao JC，Dougla SC.A robust complex FastICA algorithm using the huber M-estimator cost function［C］//7th International Conference on Independent Component A-nalysis and Signal Separation，IEEE Press，2007：152-160.

［9］MA Shexiang，GUAN Yongqiang.Space-based AIS multi-user separation based on the improved complex value FastICA［C］//2nd International Conference on Measurement，Information and Control，IEEE Press，2013：537-541.

［10］季策，王艷茹，沙明博，等.引入松弛因子的高階收斂FastICA算法［J］.東北大學學報（自然科學版），2014，35（2）：204-207.

［11］CHEN Liiuan，ZOU Xiangiun，CHEN Bingbing，et al. An improved FastICA algorithm and its application in image feature extraction［J］.Advanced Materials Research，2011，204-210：1485-1489.

［12］楊俊安，莊鎮泉，吳波，等.一種基于負熵最大化的改進的獨立分量分析快速算法［J］.電路與系統學報，2002，7（4）：37-41.

［13］史習智.盲信號處理——理論與實踐［M］.上海：上海交通大學出版社，2008：47-48.

［14］XIAO Manlin，WEI Ping，TAI Hengming.Estimation of the number of sources based on hypothesis testing［J］.Journal of Communications and Networks，2012，14（5）：481-486.

［15］GAO Li，ZHANG Tianqi，HE Danna，et al.A variable step-size EASI algorithm based on PI for DS-CDMA system blind estimation［C］//Proc 5th International Congress on Image and Signals Processing.Chongqing China.IEEE Press，2012：1730-1734.

An Improved Complex Value Fast ICA Algorithm

YIN Hongwei，LI Guolin，LU Cuihua
（Naval Aeronautical and Astronautical University，Yantai 264001，China）

An improved CFastICA algorithm was proposed to solve the problem of initial value sensibility and to improve convergence speed.First，Newton decline factor was used to optimize Newton iteration convergence direction to make the separated matrix be close to the optimal value to a certain extent，then remove the convergence factor and use the original Newton iteration realize fast convergence.Simulation results showed that the proposed algorithm had the same convergence precision with Newton decline CFastICA，and its convergence time was 52.85%less than Newton decline CFastICA.The combination property of proposed algorithm was significantly better than both of CFastICA and Newton decline CFastICA under the low SNR.

blind source separation；complex value FastICA；Newton iteration

TN974

A

1008-1194（2015）05-0022-04

2015-02-11

尹洪偉（1987—），男，江蘇徐州人，博士研究生，研究方向：目標中近程探測、識別與信息對抗技術。E-mail：yinhongwei168@126.com。