基于Serret-Frenet坐標(biāo)系的多AUV編隊路徑跟蹤控制

趙寧寧，徐德民，高　劍，張秦南

（1. 中國船舶重工集團公司 第705研究所，陜西 西安，710075； 2. 西北工業(yè)大學(xué) 航海學(xué)院，陜西 西安，710072）

基于Serret-Frenet坐標(biāo)系的多AUV編隊路徑跟蹤控制

趙寧寧1，徐德民2，高劍2，張秦南1

（1. 中國船舶重工集團公司 第705研究所，陜西 西安，710075； 2. 西北工業(yè)大學(xué) 航海學(xué)院，陜西 西安，710072）

針對多自主水下航行器（AUV）的編隊路徑跟蹤控制問題，提出了基于Serret-Frenet坐標(biāo)系的虛擬結(jié)構(gòu)編隊控制方法，分為單個AUV隊形路徑跟蹤控制，以及多個AUV間路徑跟蹤參考點的一致性協(xié)調(diào)控制兩部分。首先為每個AUV定義一個沿期望路徑運動的路徑跟蹤參考點，并以其為原點建立Serret-Frenet坐標(biāo)系描述編隊跟蹤誤差及動態(tài)模型。通過對AUV的航向角和速度的控制，使其跟蹤并收斂于該Serret-Frenet坐標(biāo)系下的期望隊形位置。然后采用基于比例-積分控制的一致性算法，調(diào)節(jié)各個參考點的路徑參數(shù)變化率使其達(dá)到一致，并以給定的期望速度沿路徑運動。通過數(shù)學(xué)仿真實現(xiàn)了3個AUV以一定隊形跟蹤期望路徑，驗證了該算法的有效性。

自主水下航行器； 編隊控制； 路徑跟蹤； Serret-Frenet坐標(biāo)系

0　引言

多自主水下航行器（autonomous underwater vehicles，AUV）通過合作和協(xié)調(diào)動作執(zhí)行任務(wù)，能夠極大地提高工作效率以及整個系統(tǒng)的可靠性［1］。作為多AUV協(xié)作中的典型性和通用性問題，編隊控制正在成為多AUV研究領(lǐng)域的熱點。

由于AUV所依賴的水聲通信特性及自身動力學(xué)系統(tǒng)的復(fù)雜性，目前編隊控制研究將信息一致性方法［2-3］和路徑跟蹤控制方法［4-5］相結(jié)合，實現(xiàn)系統(tǒng)的協(xié)調(diào)控制目標(biāo)，稱為協(xié)同路徑跟蹤控制。該方法在機器人、無人機等領(lǐng)域已有一定研究成果［6-7］，在多AUV協(xié)作系統(tǒng)也開展了一些研究［8-10］。文獻(xiàn)［8］通過構(gòu)造級聯(lián)系統(tǒng)和一致性算法實現(xiàn)直線路徑的協(xié)同跟蹤； 文獻(xiàn)［9］采用一致性算法與虛擬結(jié)構(gòu)法相結(jié)合研究了運動學(xué)層面的AUV小尺度編隊控制問題； 文獻(xiàn)［10］基于無源性理論與一致性跟蹤理論，研究了通信受限下的多AUV編隊路徑跟蹤問題。因此可知，隊形的定義基本為將一條期望路徑通過一定關(guān)系映射成多條并行路徑。

文中，采用不同的隊形定義方式，考慮多個AUV以期望隊形跟蹤空間一條期望路徑。在該期望路徑上定義編隊參考點，將其映射為該路徑上的與AUV相對應(yīng)的路徑跟蹤參考點，并建立Serret-Frenet坐標(biāo)系設(shè)計路徑跟蹤控制器［11］，使跟蹤誤差趨于由給定隊形定義的位置坐標(biāo)； 之后對所有路徑參數(shù)進(jìn)行一致性協(xié)調(diào)，使得路徑參數(shù)漸近一致，且其描述的路徑跟蹤參考點速度收斂至編隊參考點速度，實現(xiàn)編隊控制任務(wù)。

1　問題描述

1.1AUV模型

以欠驅(qū)動AUV為研究對象，其水平面運動模型［12］為

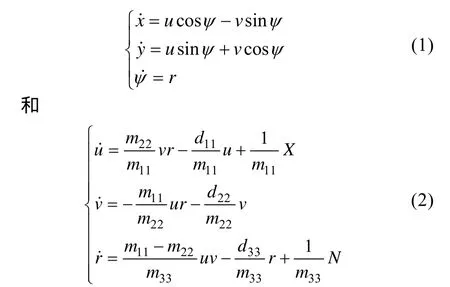
式中: u, v和r分別為前向速度、側(cè)向速度和航向角速度; x和y為AUV坐標(biāo); Ψ為航向角; X為前向推力; N為偏航力矩; m11, m22和m33為慣性質(zhì)量; d11, d22和d33為阻尼系數(shù)。

1.2基于Serret-Frenet坐標(biāo)系的路徑跟蹤誤差

給定1條光滑曲線Ω，由一般的曲線參數(shù)ξ唯一確定，O點為AUV載體坐標(biāo)系的原點，P點為路徑Ω上的路徑跟蹤參考點，在P點上建立由切向量和法向量構(gòu)成的Serret-Frenet坐標(biāo)系xsfysf，記為｛SF｝，如圖1所示。

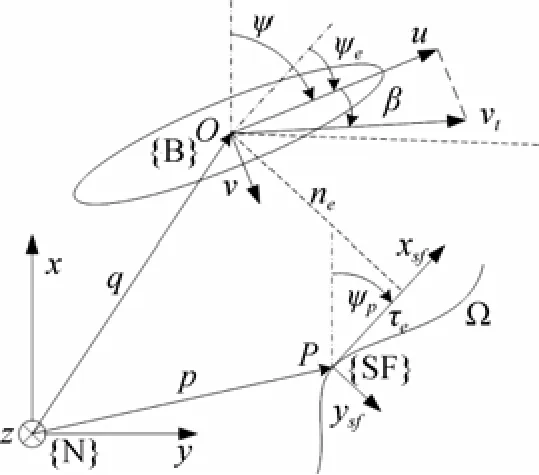
圖1　Serret-Frenet坐標(biāo)系及路徑跟蹤誤差示意圖Fig. 1　Schematic of Serret-Frenet coordinate system and path following errors

參考點以速度Up沿參考路徑Ω運動，xsf軸與地面坐標(biāo)系｛N｝的x軸夾角為Ψp。O點在｛SF｝坐標(biāo)系中的坐標(biāo)為（τe，ne），該坐標(biāo)定義了AUV的路徑跟蹤誤差。AUV前向速度與x軸夾角為Ψ，為航向角跟蹤誤差。

1.3控制目標(biāo)

考慮n個AUV組成1個整體系統(tǒng)，假設(shè)曲線Ω上P0點為該系統(tǒng)的編隊參考點，則會有P0=定義路徑跟蹤參考點Pi為AUVi對編隊參考點的估計，則有，對應(yīng)的速度其中ξi可以看作是對ξ的估計，如圖2所示。在｛SF｝坐標(biāo)系下，AUVi相對于曲線Ω的跟蹤路徑誤差為εi=li=

編隊路徑跟蹤的控制目標(biāo)分為以下步驟。

1）路徑跟蹤控制

為每個AUV設(shè)計路徑跟蹤控制器，使其最終收斂到Serret-Frenet坐標(biāo)系中由隊形定義的位置坐標(biāo)，即路徑跟蹤誤差εi最終收斂至期望坐標(biāo), 則

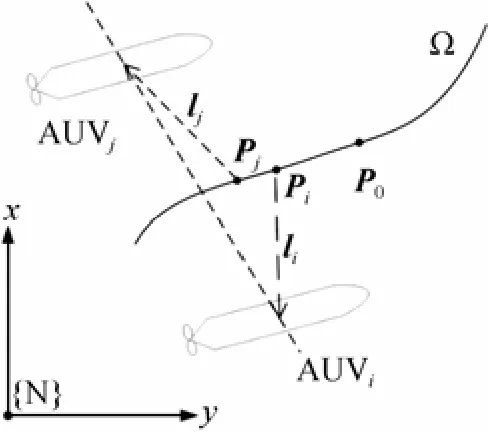
圖2　編隊路徑跟蹤設(shè)定示意圖Fig. 2　Setting schematic of formation path following

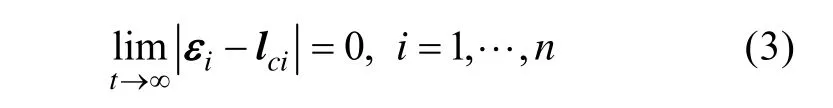
2）路徑參數(shù)一致性控制

定義vL為路徑參數(shù)ξi變化率的期望值。當(dāng)且僅當(dāng)ξi=ξj，=vL時，整個系統(tǒng)沿期望路徑形成且保持隊形勻速運動，即AUV對應(yīng)的路徑跟蹤參考點均漸近收斂到編隊參考點

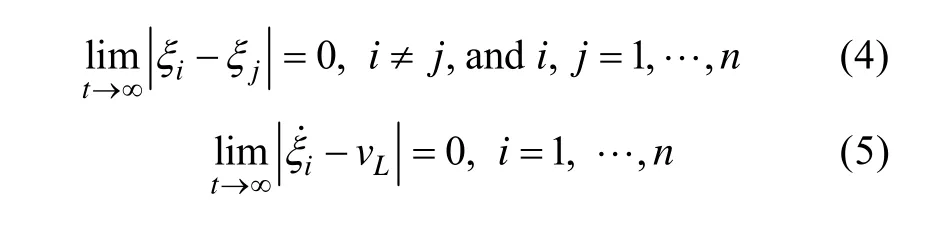
2　協(xié)同路徑跟蹤控制器設(shè)計

2.1路徑跟蹤控制

分析圖1得到AUVi跟蹤期望路徑的跟蹤誤差模型為［11］

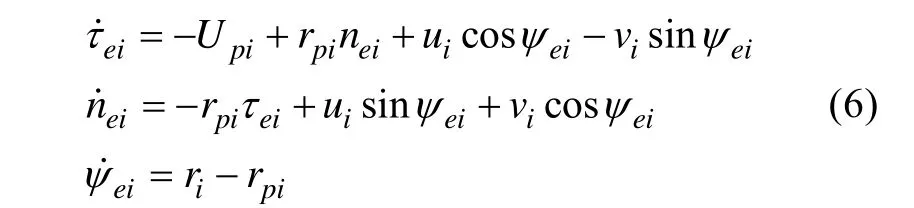
式中，rpi為參考點Pi的角速率，且

定義Lyapunov函數(shù)

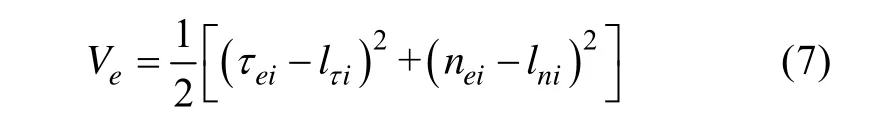
對其求時間導(dǎo)數(shù)，并代入式（6）的前2個方程，整理可得的側(cè)滑角。

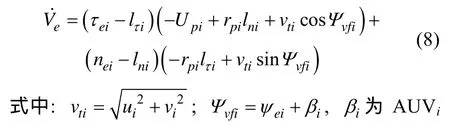
從式（8）可以看出，需要通過控制輸入Upi的作用使誤差τei-lτi穩(wěn)定，而nei-lni的穩(wěn)定則需要調(diào)節(jié)AUV的航向誤差Ψvfi來實現(xiàn)。與一般路徑跟蹤控制相比，常值隊形參數(shù)lni和lτi的存在使編隊路徑跟蹤控制更加復(fù)雜。其中，切向偏差lτi使得當(dāng)-rpilτi+vtisinΨvfi隨著nei-lni收斂到零時，有vtisinΨvfi=rpilτi≠0。因此cosΨvfi≠1，在設(shè)計參考點速度Upi時，不能消除cosΨvfi項的影響，同時rpilni中包含參考點的速度ξ.，難以分析和設(shè)計參考點速度和AUV的速度，實現(xiàn)隊形路徑跟蹤。因此，這里針對以下2種特殊情況加以研究。

1）一字型平行編隊運動

在該隊形下lτi=0，即

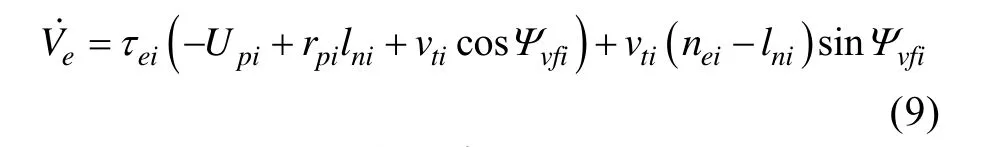
選擇AUV的航向角滿足

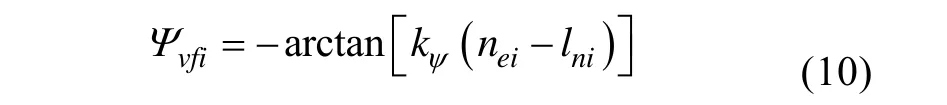
同時，選擇AUV的航行速度為

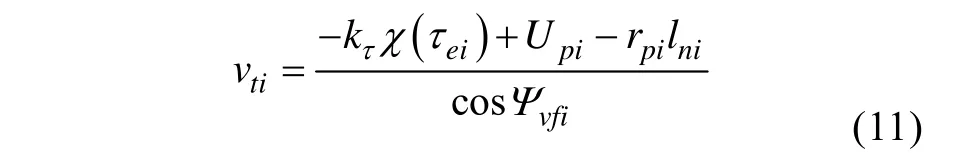
其中，χ為有界單調(diào)遞增函數(shù)，χ（0）=0，χ（τ）∈［-a，a］，且對于任意τ＜r，χ（τ）＞kχ（r ）τ，滿足

將控制輸入代入V.e方程，并考慮到

因此，當(dāng)vti＞0時負(fù)定，編隊路徑跟蹤誤差

全局一致漸近穩(wěn)定。

為了保證航行速度vti＞0，要求參考點的移動速度和角速度滿足其中rp，max為參考點沿路徑運動時的最大角速度。

2）直線參考路徑

直線是最為常見的一種路徑形式，此時rpi=0，得

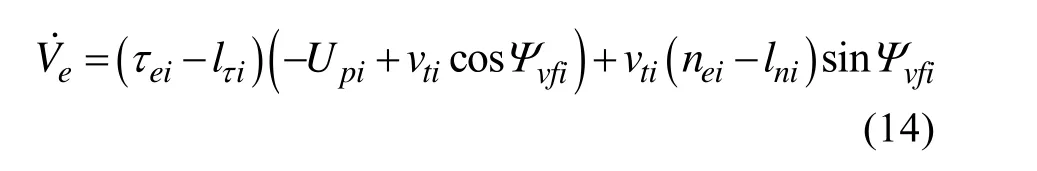
選擇AUV的航向角滿足

同時，選擇AUV的航行速度為

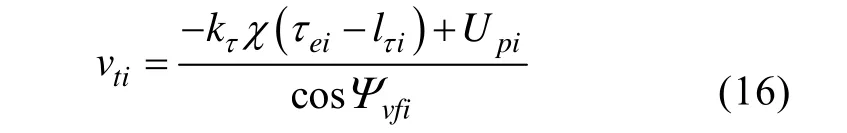
將控制輸入代入Ve.方程，并考慮到

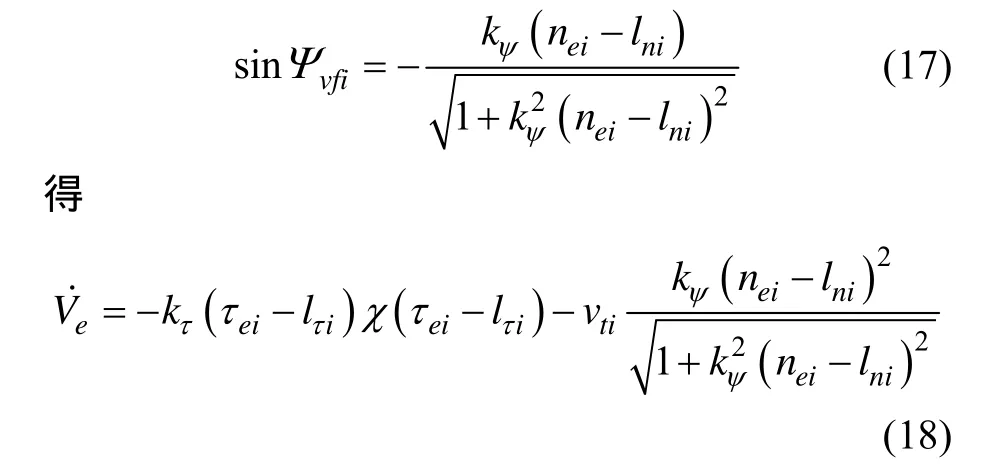
當(dāng)航行速度vti＞0時, 有V.e負(fù)定, 因此編隊路徑跟蹤誤差τei-lτi, nei-lni全局一致漸近穩(wěn)定。此時, 為了保證航行速度vti＞0, 要求參考點的移動速度滿足Upi＞kτγ。

2.2路徑參數(shù)一致性控制

假定通信拓?fù)浣Y(jié)構(gòu)圖為無向連通圖，將編隊參考點作為一個節(jié)點0放入通信拓?fù)浣Y(jié)構(gòu)圖中，令所有AUV中只有節(jié)點1知道編隊參考點的期望參數(shù)變化率，節(jié)點2和節(jié)點3分別通過與節(jié)點1和節(jié)點2的信息交互來間接獲取編隊參考點的路徑參數(shù)信息，如圖3所示。

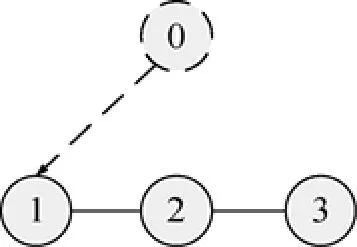
圖3　增加了編隊參考點的通信拓?fù)鋱DFig. 3　Communication topology with an additional formation reference point

由于節(jié)點2和3不能直接獲得編隊參考點的路徑參數(shù)變化率，需要通過參數(shù)自適應(yīng)算法來估計。于是，設(shè)計比例-積分一致性算法［13］

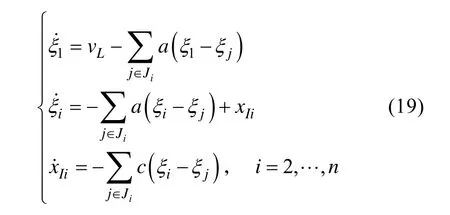
其中： 一致性參數(shù)a＞0，c＞0均為常數(shù)； Ji為與AUVi有信息交互的鄰居AUV集合。顯然，當(dāng) t→∞時，實現(xiàn)了控制目標(biāo)（4）和（5）。

3　仿真結(jié)果與分析

考慮3個AUV以三角形隊形跟蹤直線路徑，以弧長為路徑參數(shù)，直線路徑表示為：隊形定義［lτi，lni］分別為［0，0］，［-20，20］，［-20，-20］。路徑參數(shù)變化率的期望值vL=6。一致性算法中參數(shù)a=0.2，c=0.01。控制參數(shù)kτ=0.5，kΨ=5。AUV初始狀態(tài)分別為［0，10，π2］T，［10，10，0］T，［10，0，-π2］T，初始速度均為5 m/s。仿真中AUV數(shù)學(xué)模型采用美國伍茲霍爾海洋研究所的REMUS AUV數(shù)學(xué)模型［14］。

仿真結(jié)果由圖4給出。其中，圖4（a）為軌跡曲線圖，各AUV快速形成1個三角形隊形，并保持相對固定位置運動。圖4（b）～圖4（d）分別表示3個AUV的速度曲線、跟蹤誤差曲線和路徑參數(shù)曲線。圖中，ξ為路徑參數(shù)，ξ_dot為路徑參數(shù)變化率。

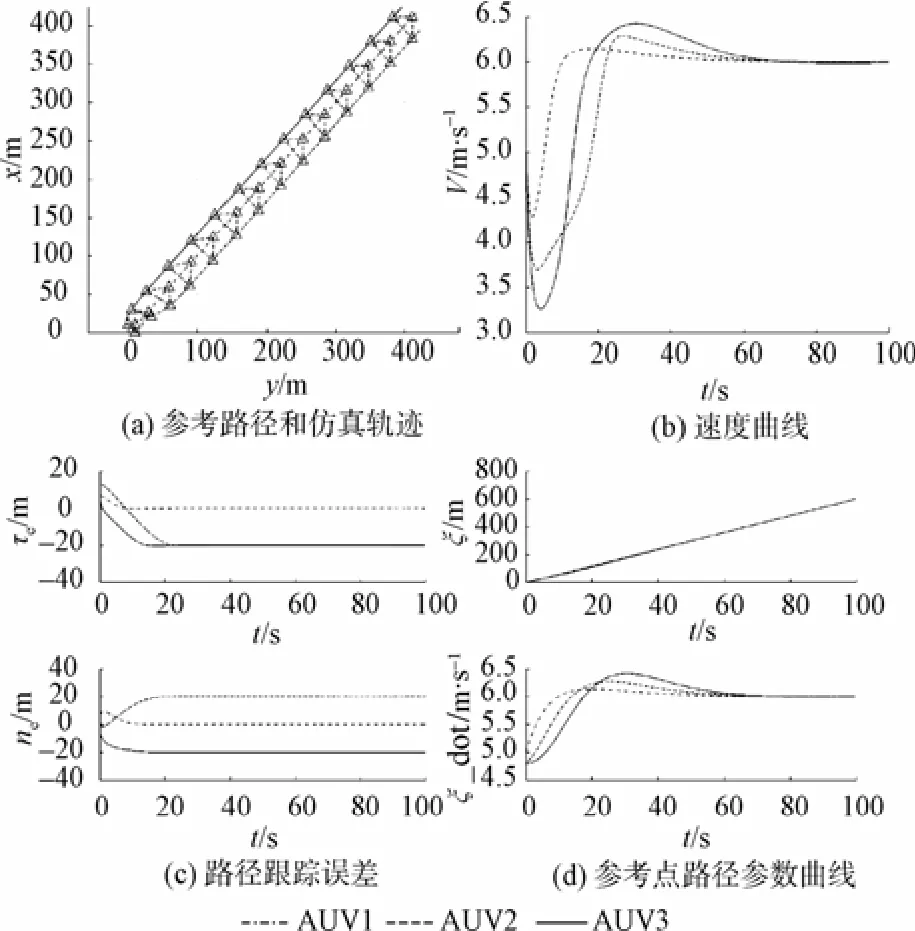
圖4　多AUV編隊路徑跟蹤控制仿真圖Fig. 4　Simulation results of the formation path following control for multiple AUVs

可以看出，AUV在運動初期不斷調(diào)整自身速度，之后快速收斂到期望速度，路徑跟蹤誤差收斂到由隊形定義的期望值，路徑參數(shù)和變化率快速一致收斂。

4　結(jié)束語

針對多AUV協(xié)作中的編隊路徑跟蹤控制問題進(jìn)行了研究。首先，考慮隊形的約束，為整個AUV系統(tǒng)設(shè)定1個編隊參考點，假定僅1個AUV知道該編隊參考點的速度（路徑參數(shù)變化率），設(shè)計路徑跟蹤算法，令A(yù)UV到自身路徑跟蹤參考點的跟蹤誤差值漸近收斂至期望值，同時設(shè)計一致性算法，令每個AUV對應(yīng)的路徑跟蹤參考點對編隊參考點的路徑參數(shù)的估計漸近達(dá)到一致。仿真結(jié)果表明，文中的算法實現(xiàn)了3個AUV以一定隊形跟蹤期望路徑，其描述的路徑跟蹤參考點速度收斂至編隊參考點速度，很好地實現(xiàn)了AUV編隊控制任務(wù)。

［1］Healey A J. Application of Formation Control for Multi-Vehicle Robotic Mine Sweeping［C］//Proceedings of the IEEE Conference on Decision and Control. New York：IEEE，2001： 1497-1502.

［2］Benediktsson J A，Swain P H. Consensus Theoretic Classification Methods［J］. IEEE Transactions System，Man，Cybernetics，1992，22（4）： 688-704.

［3］Olfati-Saber R，Murray R M. Consensus Problems in Networks of Agents with Switching Topology and Time-Delays［J］. IEEE Transactions Automatic Control，2004，49（9）： l520-l533.

［4］Do K D，Pan J. State-and-Output Feedback Robust Path-Following Controllers for Underactuated Ships Using Serret-Frenet Frame［J］. Ocean Engineering，2004，31（5/6）： 587-613.

［5］Lapierre L，Soetanto D. Nonlinear Path-Following Control of an AUV［J］. Ocean Engineering，2007，34（11/12）：1734-1744.

［6］Ren W，Sorensen N. Distributed Coordination Architecture for Multi-robot Formation Control［J］. Robotics and Autonomous Systems，2008，56（4）： 324-333.

［7］畢鵬，羅建軍，張博. 一種基于一致性理論的航天編隊飛行器協(xié)同控制方法［J］. 宇航學(xué)報，2010，31（1）： 70-74.

Bi Peng，Luo Jian-jun，Zhang Bo. Cooperate Control Algorithm for Spacecraft Formation Flying Based on Consensus Theory［J］. Journal of Astronautics，2010，31（1）：70-74.

［8］B?rhaug E，Pavlov A，Pettersen K. Straight Line Path Following for Formations of Underactuated Marine Surface Vessels［J］. IEEE Transactions on Control Systems Technology，2011，19（3）： 493- 506.

［9］袁健，唐功友. 采用一致性算法與虛擬結(jié)構(gòu)的多自主水下航行器編隊控制［J］. 智能系統(tǒng)學(xué)報，2011，6（3）：248-253.

Yuan Jian，Tang Gong-you. Formation Control of Autonomous Underwater Vehicles with Consensus Algorithms and Virtual Structure［J］. CAAI Transactions on Intelligent Systems，2011，6（3）： 248 -253.

［10］王銀濤，嚴(yán)衛(wèi)生. 多自主水下航行器系統(tǒng)一致性編隊跟蹤控制［J］. 控制理論與應(yīng)用，2013，30（3）： 379-384.

Wang Yin-tao，Yan Wei-sheng. Consensus Formation Tracking Control of Multiple Autonomous Underwater Vehicle Systems［J］. Control Theory & Applications，2013，30（3）： 379-384.

［11］高劍，劉富檣，趙江，等. 欠驅(qū)動自主水面船的非線性路徑跟蹤控制［J］. 機器人，2012，34（3）： 329-336.

Gao Jian，Liu Fu-qiang，Zhao Jiang，et al. Non-linear Path Following Control of Underactuated Autonomous Surface Vehicles［J］. Robot，2012，34（3）： 329-336.

［12］Fossen Thor I. Marine Control Systems： Guidance，Navigation and Control of Ships，Rigs and Underwater Vehicles［M］. Trondheim，Norway： Marine Cybernetics，2002.

［13］Kaminer I，Yakimenko O，Pascoal A，et al. Path Generation，Path Following and Coordinated Control for Time- Critical Missions of Multiple UAVs［C］//Proceedings of the American Control Conference，Minneapolis，Minnesota，USA，2006：4906-4913.

［14］Prestero T. Verification of a Six-degree of Freedom Simulation Model for The REMUS Autonomous Underwater Vehicle［D］. MS Thesis，MIT/WHOI Joint Program in Oceanographic Engineering，2001.

（責(zé)任編輯： 楊力軍）

Formation Path Following Control of Multiple AUVs Based on Serret-Frenet Coordinate System

ZHAO Ning-ning1，XU De-min2，GAO Jian2，ZHANG Qin-nan1
（1. The 705 Research Institute，China Shipbuilding Industry Corporation，Xi′an 710075，China； 2. School of Marine Science and Technology，Northwestern Polytechnical University，Xi′an 710072，China）

A virtual structure formation control method based on a Serret-Frenet coordinate system is proposed for the formation path following control of multiple autonomous underwater vehicles（AUVs）. The formation control system is composed of two parts，namely，the path following control for each AUV and the consistency coordination control for the path following reference points of multiple AUVs. Firstly，a path following reference point is defined for each AUV which moves along the desired path，and a Serret-Frenet coordinate system，which takes the reference point as its origin，is built to describe the formation path following errors and the dynamic model. The course angle and velocity are properly controlled to make the AUV converge to its predefined desired position in the Serret-Frenet coordinate system. Secondly，a proportional-integral consistency algorithm for path parameters is designed for all AUVs to make the virtual reference points synchronously move at a given change rate along the desired path with the desired velocity. At last，three AUVs in following a desired path with a certain formation are simulated，and the results validate the effectiveness of the proposed control method.

autonomous underwater vehicle（AUV）； formation control； path following； Serret-Frenet coordinate system

TJ630.33； TP13

A

1673-1948（2015）01-0035-05

2014-12-18；

2015-01-06.

趙寧寧（1980-），女，博士，研究方向為自主式水下航行器協(xié)同控制與仿真.