回轉體超音速入水沖擊數值仿真

孫　凱，黨建軍，郝維敏，蔣　彬

（西北工業大學 航海學院，陜西 西安，710072）

回轉體超音速入水沖擊數值仿真

孫凱，黨建軍，郝維敏，蔣彬

（西北工業大學 航海學院，陜西 西安，710072）

入水沖擊問題是現代水中兵器的研究熱點之一。采用商用CFD軟件，使用流體體積函數（VOF）模型并結合動網格技術，仿真了平頭回轉體模型在亞音速、跨音速以及超音速狀態下的入水過程，得到了模型在不同速度下的入水阻力特性、頭部直徑、液體可壓縮性及空氣激波對入水過程的影響。仿真結果表明，入水阻力系數峰值隨著速度的增加先降低后平緩，峰值寬度逐漸降低； 增大頭部直徑，阻力系數峰值增加，峰值寬度增加； 水的壓縮性會使阻力系數峰值出現的時間延后，數值降低； 空氣激波會使接觸水面時刻阻力系數降低。

平頭回轉體； 入水過程； 流體體積函數（VOF）模型； 阻力系數

0　引言

高速射彈運用超空泡技術使得自身航行阻力減小一個數量級，可用于完成攔截魚雷、擊毀水雷、破除水下障礙和獵殺蛙人等攻擊和防御任務。高速射彈的入水過程是從空中彈道轉入水下彈道的過度環節，受到巨大的沖擊載荷，可能會造成彈道失穩甚至結構失效。因此，入水過程對射彈的整個運動過程非常重要。

國外關于入水理論的相關研究始于20世紀20～30年代。G. V. Logvinovich提出的基于能量守恒的空泡截面擴張過程是最早描述空泡發展過程的理論，并成為后續理論研究的重要參考［1］。國內入水過程的理論和數值研究始于上20世紀90年代。王永虎對雷彈頭型與入水沖擊阻力特征進行了分析，得到頭型長細比對入水沖擊的影響［2］；陳宇翔等人使用流體體積函數（volume of fluid，VOF）方法研究水平圓柱砰擊入水問題，得到了湍流粘性對圓柱入水的影響［3］； 何春濤等人基于RNS方程和VOF模型對回轉體垂直勻速入水進行了數值仿真，得到了空泡形態隨時間的變化規律［4］； 邱海強等人使用混合模型對不同頭型回轉體入水過程進行了數值仿真，得到不同頭型對入水沖擊載荷和空泡形態的影響［5］。

目前，對于射彈入水問題的研究主要采用試驗和數值仿真2種方法。相較試驗研究成本高、周期長、結果不精確等缺點，數值仿真方法具有優勢。這里采用計算流體力學（computational fluid dynamics，CFD）方法，仿真了平頭回轉體模型在亞音速、跨音速以及超音速狀態下的入水過程，分析了水可壓縮性和空氣可壓縮性對入水沖擊的影響。

1　模型建立與驗證

1.1數學模型

1）Tait狀態方程

當水受到較大的壓力時，需要考慮水的壓縮性影響，文章應用的水可壓縮模型建立在Tait方程基礎上。Tait方程在仿真水下爆炸等方面應用廣泛。不含溫度修正的Tait方程為

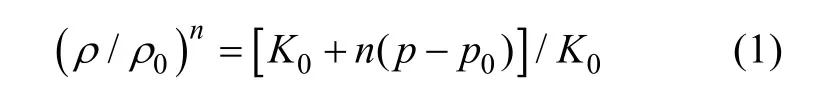
其中： p0是水的參考絕對壓力；0ρ是在參考壓力下水的參考密度； K0是在參考壓力下的參考體積彈性模量； n是密度指數； p是水受到的絕對壓力； ρ是在壓力為p時的密度。

為了使可壓縮流動中的壓力計算結果一定，需要在壓力修正方程中加入與聲速有關的項。利用可壓縮流體的聲速理論可得簡單的聲速方程

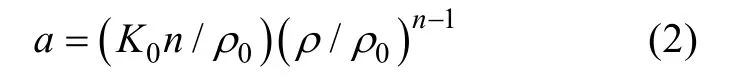
文中研究的工況涉及到跨超聲速入水，因此流體的材料屬性均使用可壓縮流體。

2）6自由度動網格模型

6自由度求解器在計算平移運動時加速度計算較精確，因而文中采用了該求解器模型。在慣性參考坐標系下建立剛體平移運動控制方程為

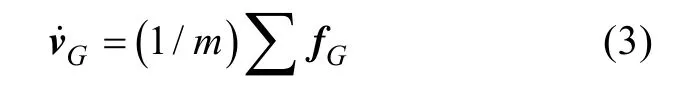
式中： v.G是質心平移加速度矢量； m是剛體質量； fG是作用在物體上的外力。文中回轉體運動通過UDF定義6自由度運動網格實現。

1.2計算模型簡化及邊界條件

建立Φ200 mm×1 000 mm的圓柱形計算域，為減小網格量，加快收斂速度，計算時選取流場的1/2。模型初始位置為水面上一定距離，在空氣中飛行一段時間整個流場穩定后再與水面接觸。

經典的高速射彈模型大多是長細比很大的回轉體，文中仿真的垂直入水工況主要研究的是入水沖擊的影響，從節省計算時間成本考慮，計算模型僅保留頭部空化器尺寸，后體采用等直徑圓柱代替，簡化后的計算模型為Φ3 mm×15 mm的平頭圓柱，并將其視為剛體。回轉體頭部阻力系數Cd計算公式為

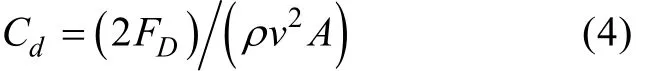
式中：FD為射彈入水過程中收到的阻力，FD= FD（t）； v為運動體入水過程中的瞬時速度，v= v（t）；ρ為水密度；A為運動體特征面積。計算流場為整個流場的1/2，該特征面積取3.532 5×10-6m2。

圖1表明了計算域各部分所采用的邊界條件：計算域下界采用壓力出口，上界采用壓力入口；遠場以及回轉體均為無滑移壁面； 計算域上部為空氣域，下部為水域； 回轉體運動使用動網格方法實現，靠近回轉體及其運動路徑附近的區域為運動區域，其余部分為靜止區域，兩部分采用interface邊界條件連接。

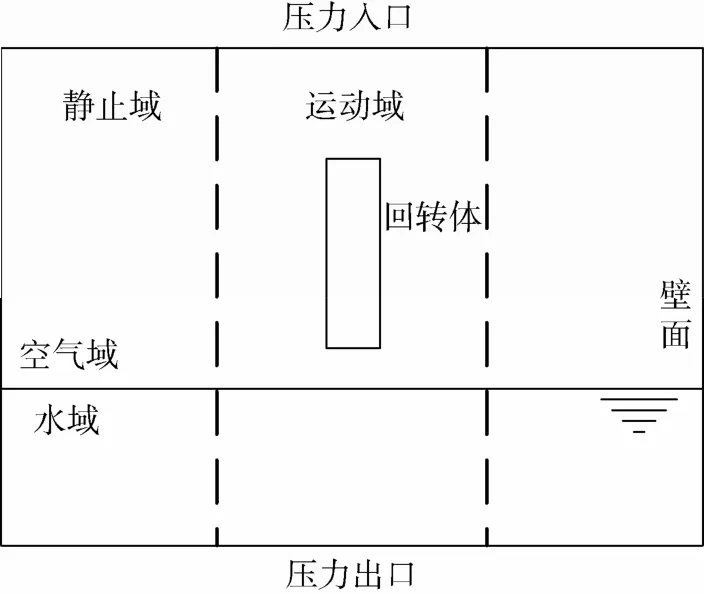
圖1　計算流場及邊界條件Fig. 1　Calculation of flow field and boundary conditions

Fluent仿真設置： 1）多相流模型選擇VOF模型，主相為水，副相為空氣和水蒸氣； 2）湍流模型選擇Realizable k-ε模型； 3）壓力速度場耦合方式選用PRESTO！； 4）水使用可壓縮流體模型； 5）開啟空化模型。

1.3模型驗證

為驗證上述計算模型的合理性，選取相關論文中的典型試驗工況進行數值仿真分析，評估其合理性。M.Schaffar等對圓柱體在1 036 m/s速度下入水進行了試驗研究，得到了該試驗工況下的流場分布［6］。

圖2給出了回轉體在入水25 cm深度后的流場分布，可以看出回轉體在水中形成了完全包裹自身的超空泡。圖3給出了回轉體入水后距離頭部不同位置處的空泡直徑，其中Serebryakov、Levinson是2種數值計算結果，Measurement是試驗得到的結果。從圖3中可以看出，文中使用的計算模型得到的結果與Serebryakov的數值仿真結果基本一致，與試驗的最大誤差不超過12.5%。

圖2　試驗與仿真結果流場對比圖Fig. 2　Comparison between experimental and simulated flow field

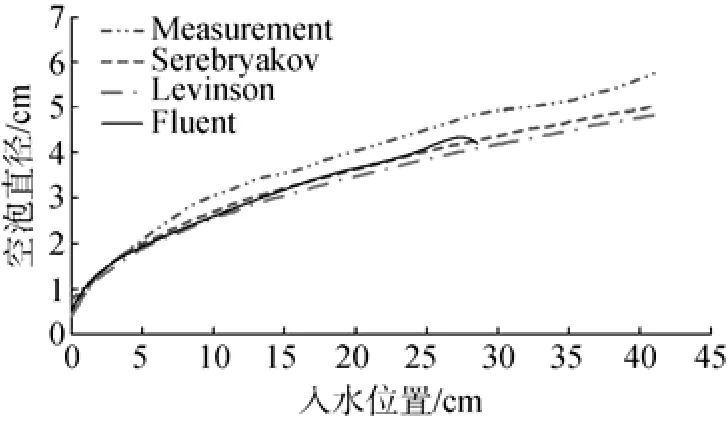
圖3　空泡外形對比圖Fig. 3　Comparison of cavitation outlines

2　仿真結果與分析

2.1回轉體高速入水流場分析

圖4和圖5顯示的是回轉體以1 000 m/s工況下不同位置處的水相云圖和蒸汽相云圖。

從圖4可看出，回轉體在入水過程中各個階段的空泡發展過程。回轉體從距離水面20 mm處開始下落，接觸水面后，水面受到沖擊向四周飛濺； 隨著回轉體繼續下落，形成開口空泡并不斷發展； 在入水深度達到2倍回轉體長度后，空泡上端依然沒有閉合趨勢。

圖4　1 000 m/s速度入水階段水相體積分數云圖

圖5　1 000 m/s速度入水階段蒸汽相體積分數云圖Fig. 5　Contour of vapor volume fraction in water entry phase at a speed of 1 000 m/s

從圖5可以看出，在空泡內氣相和水相的臨近區域產生了大量的水蒸氣。這是因為回轉體入水速度超過聲速，空氣不能及時補充進空泡內，導致空泡內的壓力低于空化壓力，產生了空化現象。正是由于空化現象，入水空泡內氣相和水相的交界面變得“凹凸不平”。

2.2速度對沖擊阻力系數的影響

圖6顯示的是回轉體以1 000 m/s速度入水過程阻力系數在峰值附近的變化過程。在空中飛行階段，由于空氣的阻力很小，阻力系數很小； 回轉體接近水面，阻力系數迅速增大，在2×10-5s時回轉體與水面接觸，此時阻力系數為2.5； 回轉體繼續運動，阻力系數增大，在2.02×10-5s時阻力系數達到最大值3.23； 阻力系數在達到最大值后逐漸降低，整個沖擊峰值持續約0.12×10-5s。

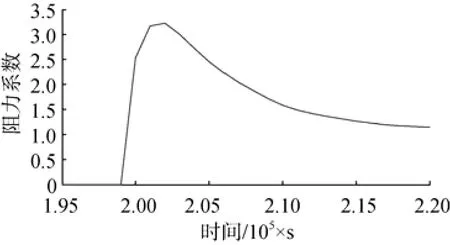
圖6　1 000 m/s速度入水阻力系數峰值放大圖Fig. 6　Enlarged view of peak value of drag coefficient in water entry phase at a speed of 1 000 m/s

圖7 顯示的是回轉體以不同速度入水時沖擊阻力系數峰值及其寬度對比。從圖7可以看出，阻力系數峰值隨著速度增加呈現先減小后平穩的趨勢。在100～300 m/s速度范圍內阻力系數峰值隨著入水速度的增加而迅速降低； 而在500 m/s及以上速度入水，沖擊阻力系數峰值降低得不明顯。入水峰值寬度時間處于10-5s量級。峰值寬度隨著速度的增大逐漸減小。在1 000 m/s及以上速度，峰值寬度改變很小。

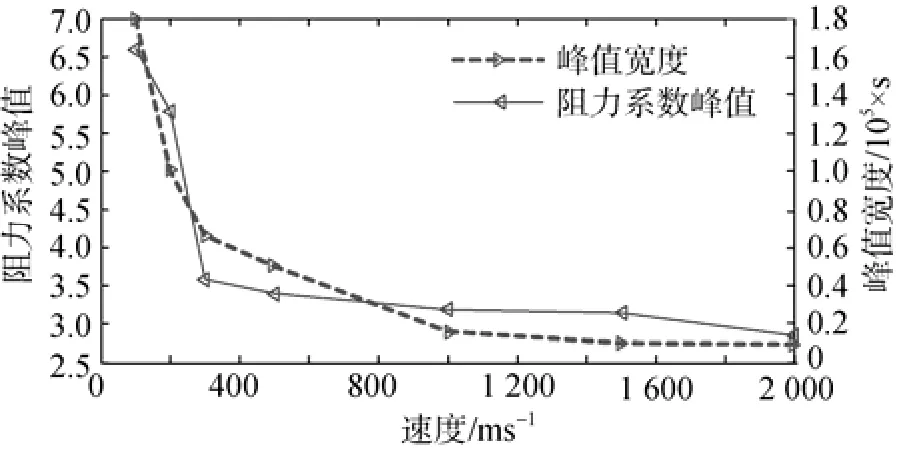
圖7　不同速度工況下阻力系數峰值和寬度對比圖Fig. 7　Comparison of peak values and peak widths of drag coefficient at different speeds

2.3頭部直徑對沖擊阻力系數的影響

計算選取速度為1 000 m/s工況，原有計算模型頭型及長度不變，頭部直徑分別擴大為原來的2倍和5倍，研究頭部直徑對阻力系數的影響。

Q 1:燃燒室輸出到水浴的熱量;Q 2:水浴傳遞給管程內LNG的熱量;C:水的熱容;T 1:水浴溫度;T 2:管程LNG的溫度;R:水浴傳熱熱阻;Gp 1:主被控對象(NG出口溫度);Gp 2:副被控對象(水浴溫度);Gc1:主回路控制器;Gc2:副回路控制器;τ:副被控對象時滯;τ1:主控對象存在時滯;J(s):燃料氣的干擾;E(s):入口LNG的干擾;GE(s):入口LNG的傳遞函數;Ge(s):前饋補償通道函數;Y 1(s):主回路的輸出;Y 2(s):副回路的輸出。

圖8顯示的是不同頭部直徑以1 000 m/s速度入水的阻力系數變化。從圖中可以看出3種直徑的阻力系數依次增大，其值分別為3.38，4.42和5.39，峰值寬度分別為1.6×10-6s，2.9×10-6s和4.5×10-6s。這是因為隨著頭部直徑變大，側向排開迎流面水的困難增加，阻力系數峰值增加，入水以后阻力系數下降緩慢。

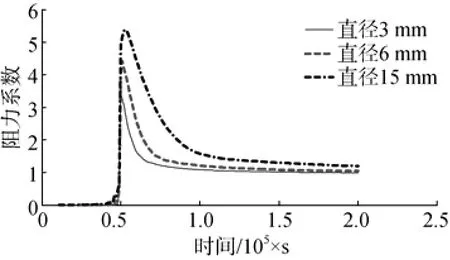
圖8　不同頭部直徑阻力系數對比Fig. 8　Comparison of different drag coefficients for different head diameters

2.4水可壓縮性對沖擊阻力系數的影響

從理論研究和生活經驗都可以知道，在沖擊速度達到一定大小后，水不能按照低速下的不可壓縮流體對待，需要考慮水的壓縮性。

圖9顯示的是不同速度工況下的水可壓縮性對阻力系數的影響。從圖中可以看出，在速度為200 m/s時，考慮水可壓縮性情況下阻力系數峰值為5.8，不考慮水可壓縮性情況下為6.2，兩者相對誤差為6.9%。同時，由于接觸水面時對水有壓縮作用，考慮水壓縮性情況下入水沖擊峰值出現的時間發生后移； 在速度為500 m/s時，考慮水壓縮性情況下阻力系數峰值出現的時間同樣發生延后，其值為3.2，而在水不可壓縮情況下沖擊阻力系數為4.4，兩者的相對誤差達到了37.5%。可見在入水速度為500 m/s時，水的可壓縮性對入水沖擊阻力影響非常巨大，不能忽略不計。

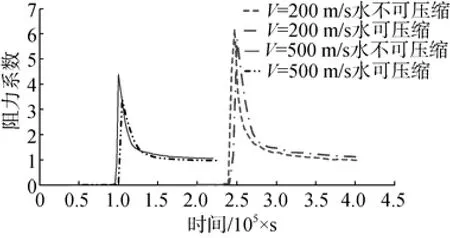
圖9　不同速度工況下水可壓縮性對比Fig. 9　Comparison of water compressibility at different speeds

2.5空氣壓縮性對沖擊阻力系數的影響

當回轉體在空氣中以超聲速運動時，會壓縮空氣產生激波。回轉體接近水面時，壓縮空氣與水相互作用是影響沖擊力的一個重要因素。計算采用如下策略： 射彈在空氣中運動時空氣和水同時使用可壓縮模型； 當射彈與水面接觸阻力系數達到峰值，關閉空氣的可壓縮性，保留水的可壓縮性直到阻力系數趨于某一穩定值，計算結束。

圖10顯示的是回轉體以1 000 m/s速度在空氣中飛行的壓力云圖。從圖中可以看出，回轉體在空氣中飛行，產生了脫體激波。當回轉體接近水面時，激波與水面相互作用使臨近的水相區域產生了壓力梯度。

圖11和圖12為速度1 000 m/s和2 000 m/s時，考慮與不考慮空氣壓縮性情況下入水阻力系數峰值的對比。從圖中可知，回轉體接近水面過程中，考慮空氣可壓縮情況下的阻力系數開始增大的時間比空氣不可壓縮要晚，阻力系數峰值出現的時間延后； 速度為1 000 m/s時，在回轉體與水接觸瞬間，考慮空氣可壓縮情況的阻力系數為2.55，不考慮空氣可壓縮情況的阻力系數為3.25，兩者相差27.5%。這是因為可壓縮空氣在回轉體接近水面過程中起到了“空氣墊”作用，使得阻力系數降低。速度為2 000 m/s時，在回轉體與水接觸瞬間，考慮和不考慮空氣可壓縮情況的阻力系數分別為2.2和2.7，兩者相差22.7%。

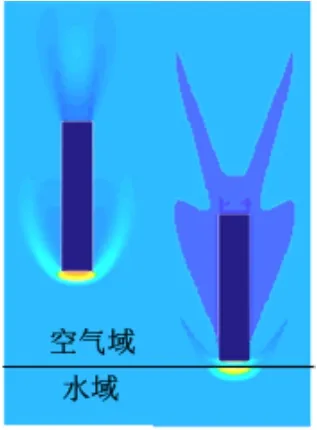
圖10　1 000 m/s速度空中飛行壓力云圖Fig. 10　Pressure contour in air for flight at a speed of 1000 m/s

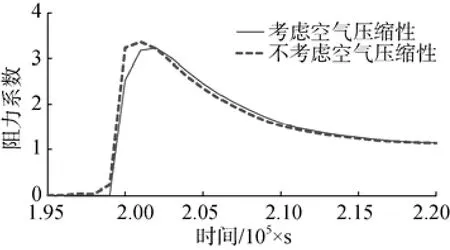
圖11　1 000 m/s速度工況空氣可壓縮性對比Fig. 11　Comparison of air compressibility at a speed of 1 000 m/s

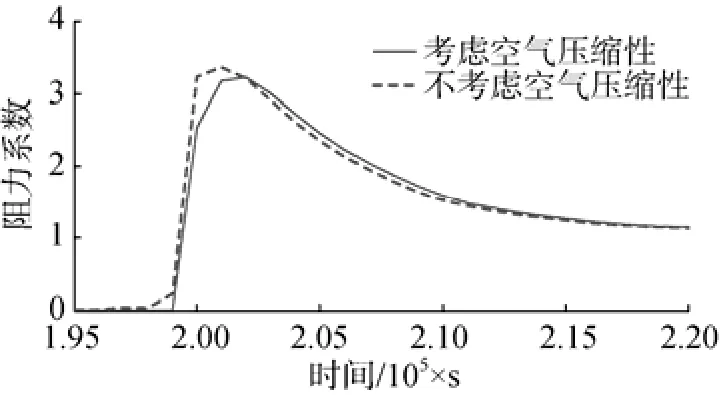
圖12　2 000 m/s速度工況空氣可壓縮性對比Fig. 12　Comparison of air compressibility at a speed of 2 000 m/s

3　結論

采用CFD方法模擬了平頭回轉體模型在亞音速、跨音速以及超音速狀態下的入水過程，分析了水可壓縮性和空氣可壓縮性對入水沖擊的影響，得到了如下結論。

1）平頭回轉體以1 000 m/s速度入水，在入水深度達到2倍體長時，入水空泡依然沒有閉合的趨勢，且在氣液兩相的交界區域附近產生了大量水蒸氣；

2）平頭回轉體入水速度在100～2 000 m/s范圍內，入水沖擊阻力系數峰值先減小后平穩。峰值寬度處于10-5s量級，其大小隨著速度的增大呈現逐漸減小趨勢； 在1 000 m/s速度工況下，增加頭部直徑，阻力系數峰值增加，峰值寬度增加；

3）考慮水壓縮性的影響，模型入水沖擊阻力系數峰值減小，峰值的時間延后。在速度為200 m/s時，考慮水可壓縮性和不考慮水可壓縮情況下，阻力系數相對誤差為6.9%； 在速度為500 m/s時，兩者的相對誤差達到了37.5%；

4）考慮空氣可壓縮性，模型接近水面時，激波與水面相互作用使臨近的水相區域產生壓力梯度。模型在空氣中運動的阻力系數增大的時間延后； 在接觸水面時刻的阻力系數減小； 阻力系數出現峰值的時刻延后。

［1］Logvinovich G V. Hydrodynamics of Free-boundary Flows［J］. Jerusalem，Israel Program for Scientific Translation，1972： 103-113.

［2］王永虎. 空投雷彈入水沖擊頭型特性參數分析［J］. 航空計算技術，2010，40（11）： 14-17.

Wang Yong-hu. Nose Performance Description Coefficience of Airborne Torpedo and Deep-mine during Water-entry Impact［J］. Aeronautical Computing Techbique，2010，40（11）： 14-17.

［3］陳宇翔，郜冶，劉乾坤. 應用VOF方法的水平圓柱入水數值模擬［J］. 哈爾濱工程大學學報，2011，32（11）： 1439-1442.

Chen Yu-xiang，Gao Ye，Liu Qian-kun. Numerical Simulation of Water-entry in a Horizontal Circular Cylinder Using the Volume of Fluid（VOF）Method［J］. Journal of Harbin Engineering University，2011，32（11）： 1439-1442.

［4］何春濤，王聰，閔景新，等. 回轉體勻速垂直入水早期空泡數值模擬研究［J］. 工程力學，2012，29（4）： 237-243.

He Chun-tao，Wang Cong，Min Jing-xin，et al. Numerical Simulation of Early Air-Cabity of Cylinder Cone With Vertial Water-entry［J］. Engineering Mechanics，2012，29（4）： 237-243.

［5］邱海強，袁緒龍，王亞東，等. 回轉體高速垂直入水沖擊載荷和空泡形態仿真［J］. 魚雷技術，2013，21（3）： 161-164.

Qiu Hai-qiang，Yuan Xu-long，Wang Ya-dong，et al. Simulation on Impact Load and Cavity Shape in High Speed Vertical Water Entry for an Axisymmetric Body［J］. Torpedo Technology，2013，21（3）： 161-164.

［6］Schaffar M，Rey C，Boeglen G. Behavior of Supercavitating Projectiles Fired Horizontally in a Water Tank： Theory and Experiments［C］//The 35th AIAA Fluid Dynamics Conference and Exhibit，Toronto，Ontario Canada，2005.

（責任編輯： 陳曦）

Numerical Simulation on Vertical Water Entry Impact of Axisymmetric Body at Supersonic Speed

SUN Kai，DANG Jian-jun，HAO Wei-min，JIANG Bin
（School of Marine Science and Technology，Northwestern Polytechnical University，Xi′an 710072，China）

Water entry impact is one of the hot topics in the modern underwater weapons research. With the volume of fluid （VOF）model and dynamic mesh in commercial CFD software，the water entry processes of an axisymmetric body with flat top are simulated at subsonic，transonic and supersonic speeds，respectively. The drag coefficient，head diameter，water compressibility and the effect of air shock wave on the water entry processes of the simulated model are acquired at three different speeds. Simulation results show that： 1）with the increase of speed，the peak value of drag coefficient first decreases then remains stable in the end，and the width of peak value decreases gradually； 2）the peak value and its width of drag coefficient increases with the increase in head diameter； 3）the water compressibility delays the appearance of the peak value of drag coefficient and reduces the peak value； and 4）air shock wave reduces the value of drag coefficient at water surface.

axisymmetric body； water entry process； volume of fluid（VOF）model； drag coefficient

TJ630.1

A

1673-1948（2015）01-0002-05

2014-11-17；

2014-12-08.

孫凱（1989-），男，在讀碩士，主要研究方向為水下航行器設計.