經歷問題解決 感悟數學思想

陳杰偉

摘要 “解決問題”的教學強調讓學生經歷問題解決的過程，在過程中掌握解決問題的方法，感悟數學思想，才能提高后繼解決問題的能力。本文結合案例談談在“解決問題”的教學中讓學生經歷問題解決過程，感悟數學思想的做法：一是從多角度著眼數學思想的定位;二是基于數學思想的探究，讓學生參與、體驗、感悟。

關鍵詞 問題解決 數學思想 小學數學

中圖分類號：G424 文獻標識碼：A DOI：10.16400/j.cnki.kjdks.2015.08.067

On Mathematical Thinking through Problem-solving Insights

——In "Mathematics Wide-angle - reasoning" Teaching Case

CHEN Jiewei

（Yuexiu District Weat Welfare Road Primary School， Guangzhou， Guangdong 510120）

Abstract "Problem solving" teaching emphasizes allow students to experience the problem-solving process， grasp solutions to problems in the process， perception of mathematical thinking in order to improve the ability to solve problems successor. In this paper， the case talk about "problem solving" teaching approach allows students to experience the problem-solving process， perception of mathematical thinking： First， focus on the positioning of mathematical thinking from multiple perspectives; the second is based on the exploration of mathematical thinking， allowing students to participate， experience and sentiment.

Key words problem solving; mathematical thinking; primary mathematics

1 著眼數學思想的定位

史寧中教授認為：數學基本思想主要指：抽象、推理和模型。人類通過數學抽象，從客觀世界中得到數學的概念和法則，建立了數學學科;通過數學推理，進一步得到更多的結論，數學學科得以發展;通過數學建模，把數學應用到客觀世界中，架起了數學與外部世界的橋梁。由數學基本思想演變、派生、發展出來的數學思想還有很多。教學前定位好數學思想，有利于深刻地理解數學的內容和知識體系，有利于以較高的觀點分析處理教材。但教學實踐中，數學思想常常通過數學方法去體現;數學方法有常常反映了某種數學思想，所以教學中，往往以數學方法去反映和體現數學思想，讓學生了解、感悟數學思想。

在本課前，筆者首先對教材進行了全面的分析，著眼數學思想的定位：從推理角度看，推理指的是由一個或幾個命題得出一個新命題的過程。推理包括合情推理與演繹推理。本課就是要借助常見的生活情境，讓學生經歷簡單的演繹推理過程，獲得演繹推理的經驗，初步掌握這種思維形式，為他們思維能力的發展打下良好的基礎。演繹推理有多種形式，教材中的例1的演繹推理用的是直接推理法與不相容選言推理，其中的選言推理不要求學生用嚴格的方式表達，但又希望能讓學生能知道這種推理方法，因此我把這里的不相容選言推理看作排除法，比較符合學生的認知特點。直接推理法與排除法是我們推理常用的基本方法，也是解決問題的一種方法，更是一種數學思想。從解決問題的角度看，小學生分析問題和解決問題的基本方法有很多，主要有模擬操作、畫圖、列表嘗試、分析與綜合、轉化等，這些方法本身蘊含了數學思想。本課我把分析與解決問題的基本方法定位為綜合法（邊閱讀邊推理法、逐步逼近的思想），畫圖（連線法、數形結合思想），列表嘗試（列表法、簡化的思想），這些方法側重點各有不同，邊閱讀邊推理法是學生口頭表達常用的方法，也符合低年級孩子分析問題總是從條件入手得出結論的習慣，而連線法書寫簡單，符合孩子少書寫的愿望，列表嘗試對簡化解決較難的推理問題非常實用，孩子都喜歡挑戰自己，自然也想學習這種方法。

2 基于數學思想的探究

數學思想的特點是抽象的、隱蔽的。定位好數學思想后，如何讓學生從直觀的解決問題過程中去感悟其中抽象的數學思想呢？解決這個問題的關鍵就是在學生經歷問題解決過程中，重視讓其參與、體驗、感悟。參與就是讓學生主動參與，包括獨立思考、合作交流等，因為沒有主動參與就不可能對數學知識與數學思想產生體驗。因此，在課堂上必須充分暴露思維過程，讓學生參與教學實踐活動，充分發揮他們的主體作用，在動腦、動手、動口的過程中領悟、體驗數學思想的形成。下面重點以新授環節的教學片斷作基于數學思想的探究。

【教學片斷一】情境導入，激發興趣（略）

【教學片斷二】親歷過程，掌握方法

（1）承接情境、呈現問題。

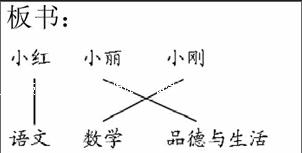
有語文、數學和品德與生活三本書，下面三人各拿一本。小剛拿的是什么書？小麗呢？（配圖：小紅拿的是語文書，小麗拿的不是數學書）

（2）提取信息、理解題意。

（3）嘗試解決、探索方法。

先獨立思考，然后把解決問題的想法與結果用自己喜歡的方式記錄下來。教師收集學生不同方法解決問題。

（4）匯報交流、體會方法。

生1：小紅拿的是語文書，那小麗和小剛拿的就是數學書和品德與生活書。小麗拿的不是數學書，可以肯定她拿的是品德與生活書，剩下小剛拿的就是數學書。

（多數學生舉手示意相同）

師：你們的方法首先從哪個已知條件開始推理的？

生齊：小紅拿的是語文書。

師：可以得到什么結論？

生齊：小麗和小剛拿的是數學書和品德與生活書。

師引導得出直接推理法，（板書：直接推理法）指出是一種基本的推理方法。

師：接著從“小麗拿的不是數學書”又可以肯定什么？

生齊：可以肯定她拿的是品德與生活書，剩下小剛拿的就是數學書。

師引導得出排除法。（板書：排除法）

師生共同小結怎樣解決這個問題，指出這種邊閱讀邊推理的解決問題的方法叫做邊閱讀邊推理法。（板書：邊閱讀邊推理法）這是一種用推理解決問題常用的方法，都用到了直接推理法和排除法兩種基本推理方法。引導說出方法的優缺點。

生齊：有序。（板書：有序）

生齊：寫起來比較麻煩。

師：那有沒有一種有序而寫起來不麻煩的方法？

生2： 我用連線法。把人名和書名寫成兩行，再根據給出的每一個條件連線：小紅拿的是語文書，直接把小紅和語文書連上線;剩下的小麗和小剛只能拿數學書和品德與生活書，小麗拿的不是數學書，可以肯定小剛拿的是數學書，小剛和數學書連線;最后把小麗和品德與生活書連線。

板書：

師小結這種邊閱讀邊推理邊連線的方法我們稱為連線法。（板書：連線法）指導連的時候先把人名寫一行，空一行用于連線，再寫出書名，接著開始邊閱讀推理邊連線，邊閱讀邊推理時都用到了直接推理法和排除法兩種基本推理方法。引導比較連線法與邊閱讀邊推理法。

生齊：一樣有序、比邊閱讀邊推理書寫簡潔。（板書：有序、簡潔）

師：還有其他不一樣的方法嗎？（學生茫然）

師介紹對解決較難的推理問題非常有用的列表法。（板書：列表法）

師出示表格，講解方法，與學生共同完成閱讀推理及符號記錄。引導比較列表法與連線法。

生齊：與連線法一樣有序、簡潔，比連線法更全面看出三個人否定拿哪些書。（板書：有序、簡潔、全面）

師：正因為全面，所以列表法對解決一些較難的推理問題非常有用。

（5）總結提升，內化方法。

師：我們剛才解決問題用的幾種推理方法都是從什么條件開始的？

生齊：小紅拿的是語文書。

師：說明這個條件為關鍵條件。我們推理時一般先找到關鍵條件，由這個條件往往能直接得到一個結論，這個結論可以幫助我們進行下一步的推理，最終推導出結論。實際推理時，我們可以根據需要選擇合適的方法，如平常口頭表達時可以邊閱讀邊推理，需要書寫時可以用連線法和列表法推理，能讓我們的推理過程更有序、全面、簡潔，特別是解決較難的問題時，可以用列表法。只有做到有序、全面，才能保證推理結果的準確性。

在上述環節中，圍繞要解決的問題，首先是自主嘗試，給學生一個大的思維空間，學生采用獨立思考、嘗試、畫圖等方法，主動探索解決問題的方法。接著合作交流，同伴互助，發揮頭腦風暴作用，初步建構問題解決的方法，并培養表達能力。又接著開展全班交流，匯報自己解決問題的過程、方法和結果，匯報完成后，適時組織有效評價，通過評價，配以比較，引導學生去除表象、掌握本質、建立模型。在開始的匯報與評價中學生掌握了推理中的直接推理法和鞏固了排除法，及分析與解決問題的邊閱讀邊推理法（綜合法），學生體驗、感悟了推理思想與步步逼近的思想;隨著匯報與評價的深入，學生掌握了連線法（畫圖），體驗、感悟了數形結合思想;最后在學生想不出列表法（列表嘗試）時，借助老師的引導講解，學生也掌握到對簡化解決較難的推理問題非常實用的列表法，體驗、感悟了簡化的思想。學生在比較不同的方法特點后，體會到哪種方法更適合自己，為學生選擇合適的解決問題的方法打下基礎。最后是總結提升，再次體悟到方法之簡單、價值，從而內化方法，建立系統的方法模型，使學生能在遇到相關實際問題時能靈活地、創造性使用方法模型來解決，也就是應用數學思想解決問題。

【教學片斷三】應用方法，鞏固拓展（略）

鞏固拓展環節安排的練習要凸顯數學思想方法的應用。因為這一環節是學生把所學到的知識一般化的過程，即運用所學知識解決相應問題的具體過程，是推理和應用模型的過程，也是學生知識深化和鞏固的環節。我安排了基本練習、操作練習、拓展練習，基本練習重在鞏固本課的重點方法——連線法，同時也不限制學生，可以選擇適合自己的方法。操作練習融趣味性、實效性于一體，用意在于通過四人小組分角色進行推理，體會到模擬操作也是解決問題一種很直觀、適用的方法，豐富學生的方法。拓展練習在于打破學生的思維定勢，促使學生真正動腦思考，并能運用剛剛新課中學到的多種思想正確分析問題、解決問題。

教學實踐證明，在小學“解決問題”的教學中，讓學生經歷問題解決的過程，在過程中掌握解決問題的方法，感悟數學思想，是提升學生后繼解決問題的能力的重要舉措。