教育“無痕” 精彩“有跡”

徐 斌 江蘇省特級教師，中學高級教師，江蘇“人民教育家工程”培養對象，教育部“國培計劃”首批特聘專家，人大復印資料《小學數學教與學》編委。

1992年獲江蘇省小學數學優質課比賽第一名，2000年獲全國小學數學觀摩課評比一等獎。曾應邀為全國第五屆小學數學學術年會上觀摩課，在《小學數學教師》等20余家刊物發表論文400余篇，應邀到全國20多個省、市、區講學400余次。教育事跡在《人民教育》“名師人生”欄目作專題報道，《中國教育報》曾七次連載了“徐斌教育教學藝術系列報道”。出版專著《追尋無痕教育》《為學生的數學學習服務》《推敲新課程課堂》《另類課堂》及“中國名師”系列教學光盤。其教育主張是無痕教育，課堂教學風格穩健厚實。

無痕，從字面上講，就是沒有痕跡，不留印記，一切如初。“痕”本意是指創傷痊愈后留下的疤痕，也泛指斑跡。無痕，常被作為一種美學境界被眾多文人墨客所描繪。賈島《江亭晚望》：“鳥歸沙有跡，帆過浪無痕。”蘇軾《與潘郭二生出郊尋春》：“人似秋鴻來有信，事如春夢了無痕。”杜甫的《春夜喜雨》更是描繪了一幅無痕美景：“隨風潛入夜，潤物細無聲。”

無痕被用于教育，早已有之。無痕教育，是指“把教育意圖與目的隱蔽起來，通過間接、暗示或迂回的方式，給學生以教育的一種教育方式”（盧克謙《無痕教育：具有美學韻味的教育方式》）。無痕教育的提出，雖來源于德育領域，但其所彰顯出來的人性化和科學性光輝，足可以指導一切學科教學行為。蘇霍姆林斯基曾說，“造成教育青少年困難的最重要原因，在于把教育目的在學生面前以赤裸裸的形式進行”“把教育意圖隱蔽起來，是教育藝術十分重要的因素之一”。杜威在論述什么是教育時指出：“一切教育都是通過個人參與人類的社會意識而進行的。這個過程幾乎是出生時就在無意識中開始了。”“由于這種不知不覺的教育，個人便漸漸分享人類曾經積累下來的智慧和道德的財富。”無痕教育不僅是一種教育方式，更是一種教育思想，是一種教育心理學的規律和原則，是一種教育的美學和哲學境界，是一種對教育本原的追尋。

在小學數學教學中，如何實施“無痕教育呢”？筆者以“解決問題的策略”的教學為例，談幾點體會。

一、不知不覺中開始

讓學生在不知不覺中開始學習，是無痕教育追尋的基本境界。不知不覺中開始，從教育心理學角度看，是確立合適的學習起點，即明確學生“現在在哪里”。有了對教學內容的整體把握，就有了對學生原有認知與學習狀態的準確了解，就有了對學生生活經驗與思維體驗的適度掌握。有了這樣的教學前提，就能夠進一步明確把學生“將要帶向哪里”以及“如何走向那里”，從而無痕地將學生引向新知的邊緣，讓學生對新知學習的需求油然而生。

【案例1】《解決問題的策略：一一列舉》的課堂引入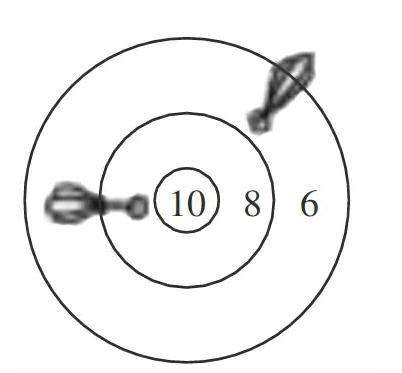

師：請看，在我們日常生活當中，經常會遇到這樣的現象——飛鏢游戲，玩過嗎？

生：玩過。

師：這是飛鏢的靶子，如果讓我們全班每人都來投一鏢，大家有可能得多少環呢？

生：有可能是10環，8環，6環。

師：（相應板書）還有其他可能嗎？

生：可能是0環。

師：對，可能連靶子都沒有射上，那就是0環。

師：這些都是可能的結果，現在老師把它們都——

生：列舉出來了。

師：說得很好！（板書：列舉）列舉就是一種策略，那剛才為什么要把它們列舉出來呢？

生：我覺得應該是要知道它一共有多少種可能。

師：對，把每一種可能都列出來，那不是一般的列舉，叫作一一列舉。今天這堂課，我們就來學習一一列舉的策略。

上述教學片段，從學生十分熟悉的飛鏢游戲引入，從探索“每人都投一次，可能得多少環”這一問題入手，讓學生從生活現象中發現數學問題，從而引出“一一列舉”的策略。這樣的新課引入，學生似乎在回憶生活經歷，又似乎在體驗游戲活動，又似乎在探尋數學規律，學生在不知不覺中自然地把生活經驗與數學方法聯系起來，從而生發出對一一列舉策略的探究欲望。

可見，在課堂學習的起始階段，從學生熟悉的生活問題出發，讓學生捕捉數學信息，發現數學問題，提出數學問題，使學生了解知識的產生源頭，能溝通起數學與生活的密切聯系，為數學模型的建立打下現實基礎。

二、潛移默化中理解

“教是為了更好地學。”對知識和方法的理解是學習的重要目標。小學階段，兒童的認知水平處于皮亞杰指出的“具體運算思維”階段，其最大特點是思維離不開具體事物的支持，這也導致小學生的感知覺、觀察力和記憶均處于初步發展水平，其學習數學的動機和興趣很不穩定。在這樣的前提之下，兒童學習數學的過程，需要充分借助形象直觀的教學手段，充分利用新舊知識的相互作用，以順應兒童的學習心理，讓兒童在不露痕跡中獲得新知，在潛移默化中理解數學本質。

【案例2】《解決問題的策略：替換》的建模過程

例題：小明把720毫升果汁倒入6個小杯和1個大杯，正好都倒滿。小杯的容量是大杯的。小杯和大杯的容量各是多少毫升？

變式：小明把720毫升果汁倒入6個小杯和1個大杯，正好都倒滿。大杯的容量比小杯多20毫升。小杯和大杯的容量各是多少毫升？

結合學生的探索逐步完成板書：

1+6720+620]

師：變式題與剛才的例題在解法上有什么不同？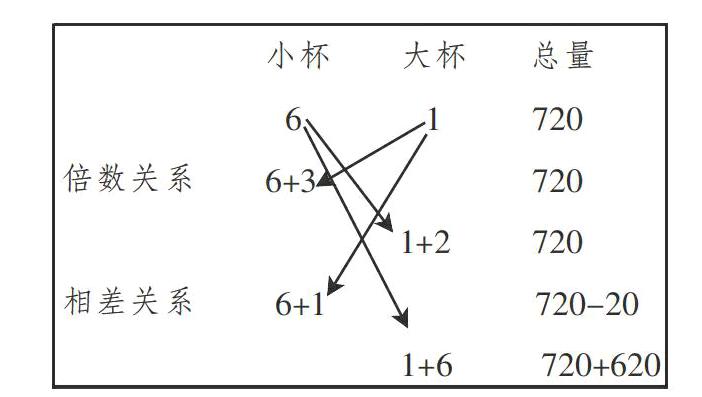

生1：替換依據不同。例題中，兩個數量是倍數關系；變式題中，兩個數量是相差關系。

生2：替換后的總量不同。例題中，替換后總量還是720毫升；變式題中，替換之后的總量發生了變化，變多了或者變少了。

師：是啊！由于替換的依據不同，替換后的總量會不一樣。如果我們觀察替換前后杯子的個數，你有什么發現？

生1：倍數關系的替換，替換之后杯子的總個數變化了。

生2：相差關系的替換，替換之后杯子的總個數沒有變化。

師：同學們觀察得真仔細！數學就是這么奇妙！在變與不變中存在著內在的聯系。

上述案例在幫助學生理解和建立替換策略的數學模型時，首先讓學生分別探索和經歷了倍數關系和相差關系的替換過程，然后對兩種典型替換進行對比，使學生發現兩種替換的異同點，并溝通起兩種關系替換的內在聯系，對替換策略的數學模型有深入的認識，促進學生良好認知結構的形成。這樣的學習過程，不是把解題策略灌輸和傳遞給學生，而是讓學生動手實踐與自主探索、觀察對比與聯系內化，在潛移默化中理解替換策略的本質，并對兩種典型的替換類型有深刻的認識。

可見，學生建立數學模型的過程，一方面需要讓學生運用數學語言和符號分析問題，另一方面也需要讓學生在建立數學模型的同時獲得結構化的理解。因此，數學模型的建立過程，需要讓學生充分經歷、體驗和探索，在潛移默化中獲得對模型豐富性和深刻性的認識。

三、循序漸進中掌握

學生學習數學的過程，既是在教師引導下的意義建構過程，也是在自身需求發展中的自主建構過程。無痕教育視野下的學生數學學習過程，更主要地體現為教師精心設計學生的學習進程，從某種意義上說是一種“進”與“退”的藝術。通過適當的“退”和必要的“進”，能使學習過程成為學生潛移默化地掌握知識和技能的過程。在課堂上，“進”“退”之間體現的是一種行云流水般的從容節奏，是一種水乳交融般的無痕狀態。

【案例3】《解決問題的策略：畫圖》的練習片段

原題——“張莊小學原來有一個長方形操場，長50米，寬40米。”讓學生首先在腦中畫圖，然后逐步變化條件和問題，不斷讓學生腦中畫圖猜測，并在紙上畫圖驗證結果。

變式之一：“在修建時，長增加8米，面積增加多少平方米？”學生很快在腦中畫圖，甚至不需要在紙上畫圖，即可用手勢比劃出圖像（圖1），并列出算式40×8=320（平方米）。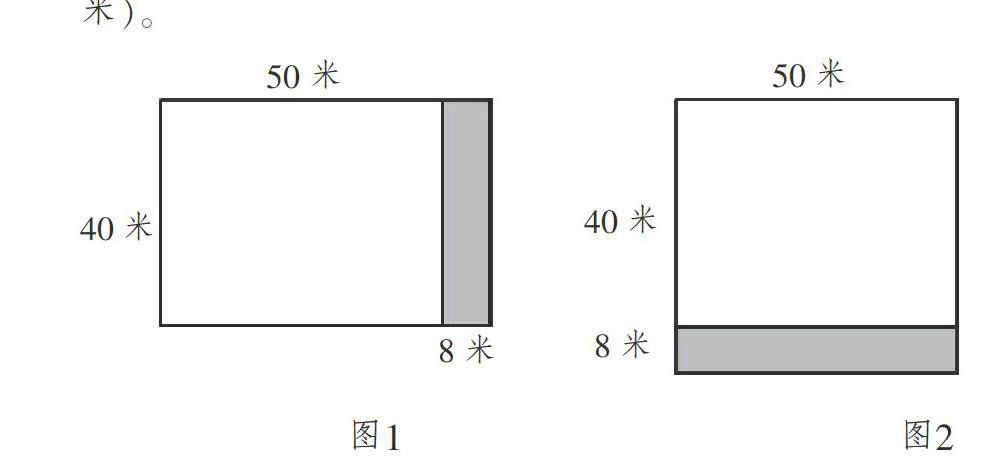

變式之二：“在修建時，寬增加8米，面積增加多少平方米？”有了前面的經驗，學生更加熟練地腦中畫圖（圖2），并列式解決問題50×8=400（平方米）。

變式之三：“在修建時，長和寬各增加8米，變成新的長方形。面積增加多少平方米？”老師剛出示完題目，不少學生即快速搶答：“面積增加720平方米，列式是320+400=720。”

在學生畫圖列式之后，教師再次提出：經過頭腦里畫圖猜想和在紙上畫圖驗證，大家發現面積增加的部分是720平方米嗎？這是什么緣故呢？同時結合學生的畫圖進行展示和解釋，從而突破學習難點（從圖3逐漸演變為圖5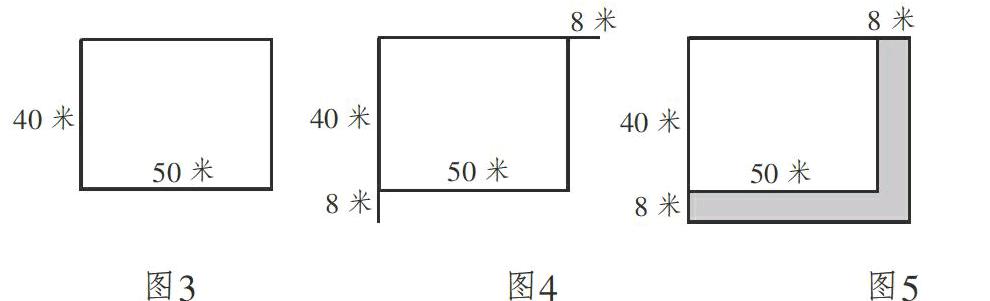）。 有了以上三次變式，學生積極性高漲，對畫圖策略的探索興趣更濃，教師繼續出示了以下三次變式：

變式之四——“修建時，長和寬各減少8米，操場的面積減少多少平方米？”

變式之五——“修建時，長增加8米，寬減少8米，面積改變嗎？為什么？”

變式之六——“修建時，長減少8米，寬增加8米，面積改變嗎？為什么？”

以上教學設計和組織，讓學生邊畫圖邊思考，邊猜測邊驗證，邊對比邊討論，不斷發展學生的幾何直觀水平，使學生不斷體驗到畫圖策略的價值所在。這種一題多變的方式，緊緊圍繞畫圖策略，讓學生不斷猜測、驗證、聯想、推理，經歷不同情形下的數形變化過程，探究圖形變化中的內在規律，引導學生在數學思維活動中逐步積累數學活動經驗，讓學生在運用畫圖策略解決實際問題的過程中深入探索變化規律，享受數學思維活動的快樂。

可見，“進”與“退”的過程，是學生潛移默化地掌握知識技能的過程，是學生不露痕跡中培養思維能力的過程，是學生淡墨無痕中發展數學思維的過程。從這個意義上說，數學教學的智慧就在于教師能在“進”與“退”之間游刃有余。

四、春風化雨中提升

課堂是師生人生中一段重要的生命經歷，課堂是充滿無限魅力的地方，課堂是學生充分發展的天空。無痕教育理念指導下的數學課堂，是學生享受教師服務的過程，也是學生自主學習、主動發展的過程。這樣的過程，學生的學習經歷應是充實快樂的，學習結果是充分有效的，學習過程是充滿智慧的。理想的課堂教學過程，似雪落春泥，悄然入土，孕育和滋潤著生命。雖無痕，卻有聲有色，有滋有味；雖無痕，卻如歌如樂，如詩如畫。

【案例4】《解決問題的策略：轉化》的新知展開

（1）回顧公式推導的經歷。

啟發思考：其實，在我們小學階段的數學學習中，比如說一些圖形面積公式、體積公式的推導，就常常用到轉化的策略，你們能想起來嗎？

反饋交流（根據學生的回答，課件相機呈現公式的推導過程）。

（2）感受轉化策略的作用。

回顧：我們在推導平行四邊形、三角形和梯形的面積計算公式時，是先知道哪個圖形的面積計算公式的？接下來我們是如何研究圖形之間的面積關系的？我們又是把哪些圖形轉化成平行四邊形（三角形、梯形）的？長方體、圓柱和圓錐的體積計算公式呢？

感受：在剛才應用轉化策略推導出這些公式時，你們發現它們都有什么共同的特點？（轉化前這些問題都是我們面臨的新問題，而我們都是把它轉化成曾經學習過的舊知識。）

（3）拓展轉化策略的應用。

想一想：在學習認數和計算時，哪些地方用到過轉化的策略呢？

練一練：計算+++。

提問：你能運用轉化的策略來解決這一問題嗎？

上述案例中，主要從三個層面讓學生經歷轉化策略的形成過程：（1）圖形面積、體積方面的應用；（2）圖形周長、內角和方面的應用；（3）數與計算方面的應用。在轉化策略的形成過程中，遵循學生的心理規律，逐步深入展開，首先讓學生經歷直觀的單一圖形的轉化，接著讓學生經歷形與形之間的轉化，然后再讓學生經歷數與計算方面的轉化。不同層面的轉化策略，思維含量是不一樣的，分類讓學生經歷轉化策略的形成過程，符合學生“感知—表象—抽象”的認知規律。

可見，建立數學模型之后，為了讓學生對初建模型有充分的感性積累，應該讓學生運用數學模型解決同類數學問題，在解決數學問題的過程中，積累數學活動經驗，獲得對數學模型的深刻理解，形成初步運用數學模型的相關技能，提升學生的數學思想，培養學生的數學素養，為進一步解決實際問題打下堅實基礎。?