碼垛機器人運動學幾何解法的研究*
□郭小寶 □趙 振 □陳落根杭州娃哈哈集團機電研究院智能裝備研究所 杭州 310020
碼垛機器人運動學幾何解法的研究*
□郭小寶 □趙 振 □陳落根
杭州娃哈哈集團機電研究院智能裝備研究所 杭州 310020
機器人的正向、逆向運動學是機器人運動控制系統與機械系統連接的橋梁,其封閉解問題至今還沒有通用的解法,比較通用的是代數方程組的數值迭代算法,通常難以保證實時性和精度要求。基于幾何方法通過分析碼垛機器人的機構特點簡化運動學模型,詳細推導正向運動學和逆向運動學解法,推導過程簡單、直觀。最后通過MATLAB編程和SolidWorks三維實體模型運動仿真,驗證幾何解法的正確性。
多關節重載碼垛機器人在工業生產搬運領域占有重要市場,隨著中國制造自動化進程的加快,得到越來越多的應用[1-2]。
機器人的正向、逆向運動學是機器人運動控制系統與機械系統連接的橋梁,是指導機器人動作指令的核心部分,簡單且能夠快速執行的運動學算法是機器人實現高速、高精度運行的重要手段[3-4]。
機器正向運動學是已知關節變量,求解末端執行器的空間位置和姿態;逆向運動學是已知末端執行器的位置和姿態來求解關節變量。機器人運動學算法主要有解析法和數值法,解析法根據機構的結構組成特征建立約束方程組,采用多種方法從約束方程組中消去中間參數,獲得單參數多項式后再求解,方法包括矢量代數法、幾何法、矩陣法和四元數法等,優點是可以得到全部解,缺點在于難度較大,方法通用性不好。數值法是直接求解約束方程組,可以通過迭代運算求得任何機構的實數解,但一般不能得到全部解,一般而言,初值選取及搜索算法對收斂性和精度影響較大[5-7]。
筆者通過分析碼垛機器人的機構特點,簡化運動學模型,基于傳統幾何方法,詳細推導正向運動學和逆向運動學解法,推導過程力求簡單、直觀。最后通過實際工程實例,采用MATLAB編程和基于SolidWorks三維實體模型運動仿真,驗證幾何解法的準確性。
1 碼垛機器人運動學模型
圖1所示的是雙平行四邊形碼垛機器人,其基礎部件包括底座、腰部、大臂、小臂、手腕、末端法蘭,實現空間范圍內的三平動和繞腰部軸線轉動的4個自由度。由三角架及其連桿從動部件與大臂和小臂構成三組平行四邊形,實現在搬運過程中末端手腕的水平。
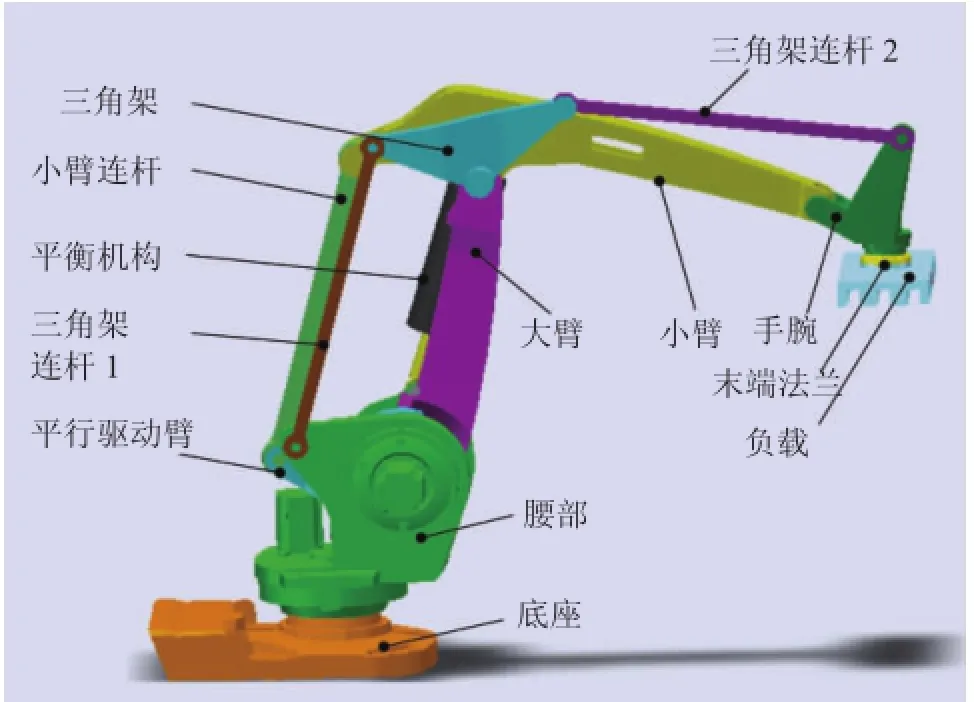
圖1 關節型碼垛機器人三維模型
機器人的機構簡圖如圖2所示,Oi-xiyizi(i=0~5)分別為底座、腰部、大臂、小臂、手腕、末端法蘭的轉動中心和連體坐標系,θi(i=1~5)分別為其轉動關節的關節變量,di、ai為機器人的桿長參數。
考慮機構運動特點,可以將圖2簡化為圖3,機器人末端法蘭的連體坐標系O5-x5y5z5在底座的連體坐標系O0-x0y0z0下的位置坐標為x、y、z和歐拉角姿態坐標(Z-Y-Z順規)為φ、ψ、θ,考慮到機構為四自由度機器人,具備三移動和繞Z軸轉動的4個自由度,從而φ=0、ψ=0。
機器人的桿長參數和關節變量見表1。
基于平行四邊形特點,驅動關節變量滿足:
θ3=-θ2-θ4(1)
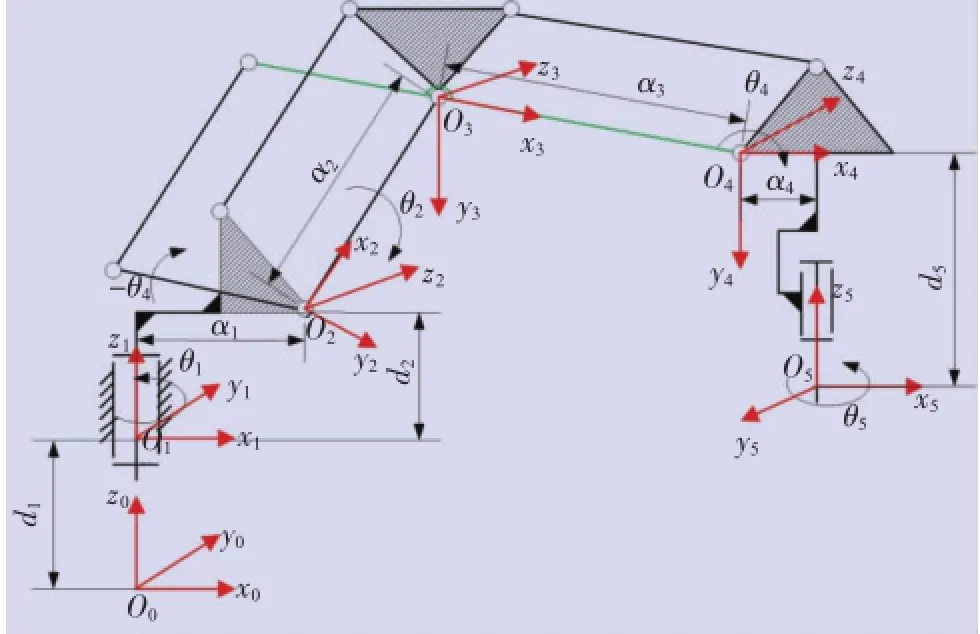
圖2 機器人機構簡圖
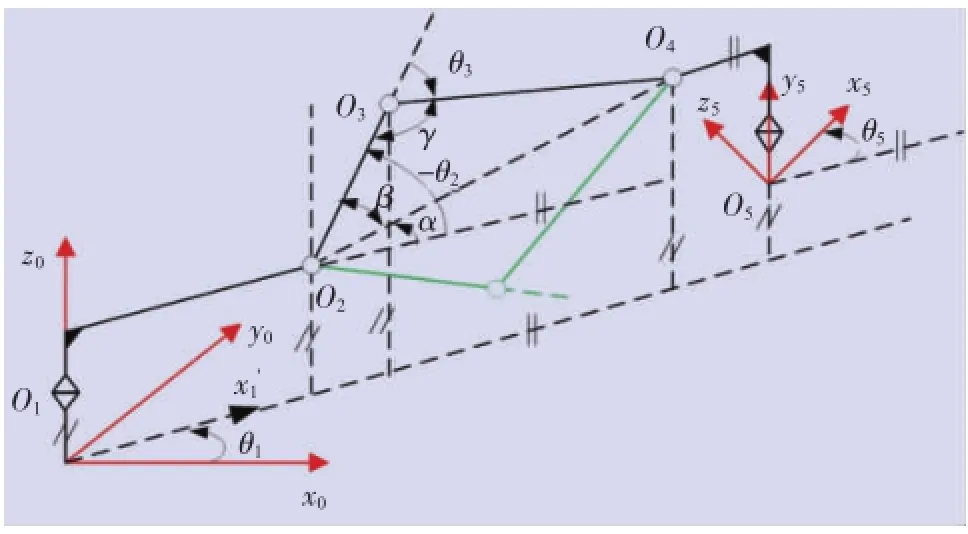
圖3 機器人簡化機構簡圖

表1 機器人桿長參數和關節變量
從而機器人的4個獨立驅動關節變量為腰部關節θ1、大臂關節θ2、腕部關節θ4和末端法蘭θ5。
機器人回零狀態(大臂豎直,小臂水平)下:θ1=0°,θ2=-90°,θ3=90°,θ4=0°,θ5=0°。
2 運動學幾何解法分析
機器人運動學指機器人驅動關節變量與末端剛體獨立位姿坐標之間的映射關系。
2.1 正向運動學
求解操作空間變量:u=(xy zθ)T
由圖3容易求得末端法蘭相對于底座連體坐標系的轉角θ:
θ=θ1+θ5(2)
θ3根據式(1)求得。
在x'0軸和z0軸構成的平面內,O0O5沿x'0軸的分量可表示為:
l1=a1+a2sinθ2+a3sin(θ2+θ3)+a4(3)
O0O5沿z0軸的分量即z為:
z=d1+d2+a2cosθ2+a3cos(θ2+θ3)+d5(4)
末端法蘭的連體坐標系O5-x5y5z5在底座的連體坐標系O0-x0y0z0下的位置坐標x、y可通過l1求出:
x=l1cosθ1
y=l1sinθ1(5)
從而完成正向運動學求解,表示為:
x=(a1+a2sinθ2+a3sin(θ2+θ3)+a4)cosθ1
y=(a1+a2sinθ2+a3sin(θ2+θ3)+a4)sinθ1
z=d1+d2+a2cosθ2+a3cos(θ2+θ3)+d
θ=θ1+θ5
2.2 逆向運動學
根據式(5),關節1轉角θ1容易由x、y求出,考慮到反正切函數不能確定θ1所在象限,從而通過四象限反正切函數求得:
θ1=arctan[2(y,x)] (7)
由式(2)可求出θ5:
θ5=θ-θ1(8)
在三角形△O2O3O4中,邊O2O4可用已知末端法蘭的坐標值求得,記為m:
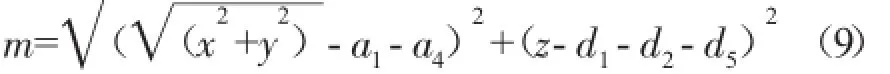
O2O4相對于x'0軸的夾角為α,可用已知末端法蘭的坐標值求得:
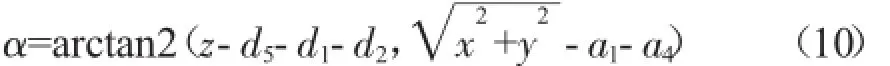
三角形△O2O3O4中∠O3O2O4設為β,根據余弦定理可得:同理,求∠O2O3O4,記為γ:


由于機構特點,θ2和θ3會有兩組解:{θ2=-α-β
θ3=180°-γ或(13)
θ3根據式(1)求得。從而完成逆向運動學求解。
3 工程實例驗證
3.1 MATLAB驗證
在MATLAB開發環境下,根據前文的幾何算法編寫如圖4所示的正向、逆向運動學算法腳本,腳本不足30行代碼,完全順序結構,沒有任何數值迭代,具有很高的執行速度。

圖4 運動學算法的MATLAB腳本截圖
運動學測試點見表2,通過MATLAB校驗,測試點滿足正向運動學和逆向運動學算法,從而驗證了幾何解法的有效性和正確性。
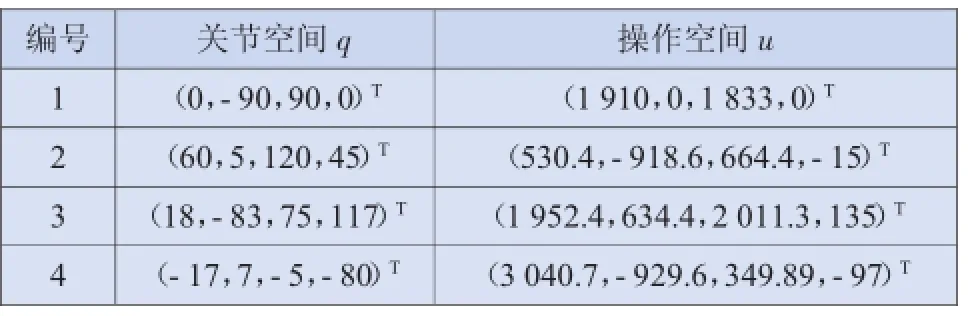
表2 運動學算法驗證點對應關系
3.2 運動仿真驗證
為了反映運動學幾何算法的真實性,在Solid-Works三維建模軟件下,設計真實的碼垛機器人模型,定義好配合和約束條件,為運動學仿真準備。
首先,規劃機器人工作空間末端法蘭的運動軌跡,即逆向運動學的輸入u=(x y z θ)T,其中x=1 000 mm,θ=0°,在y-z平面的軌跡如圖5所示。
通過逆向運動學和軌跡規劃,計算出各驅動軸的關節角位移,如圖6所示。
將各關節的角位移導入基于SolidWorks設計的碼垛機器人模型作為各關節驅動馬達的輸入量,經過實時運動仿真,獲得如圖7所示的真實模擬軌跡,該仿真的軌跡與預先規劃的軌跡完全一致,從而驗證了幾何運動學解法的正確性。
4 結論
基于幾何學方法研究了雙平行四邊形碼垛機器人運動學的解析算法,得出了以下結論。
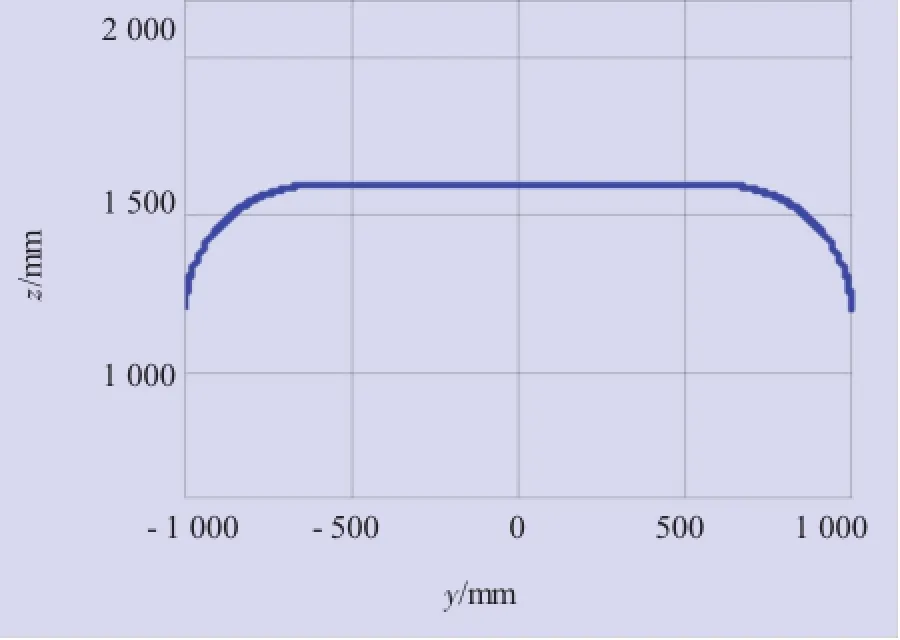
圖5 機器人末端控制點在y-z平面內軌跡
(1)分析了雙平行四邊形碼垛機器人,它是三平動一轉動的機構,獨立驅動的關節分別為腰部、大臂、手腕和末端法蘭。
(2)建立了機器人的機構簡化模型,為幾何法求解運動學奠定了基礎。
(3)基于立體幾何和矢量的方法,詳細推導了正向運動學和逆向運動學算法,獲得了簡單直觀的運動學計算公式。
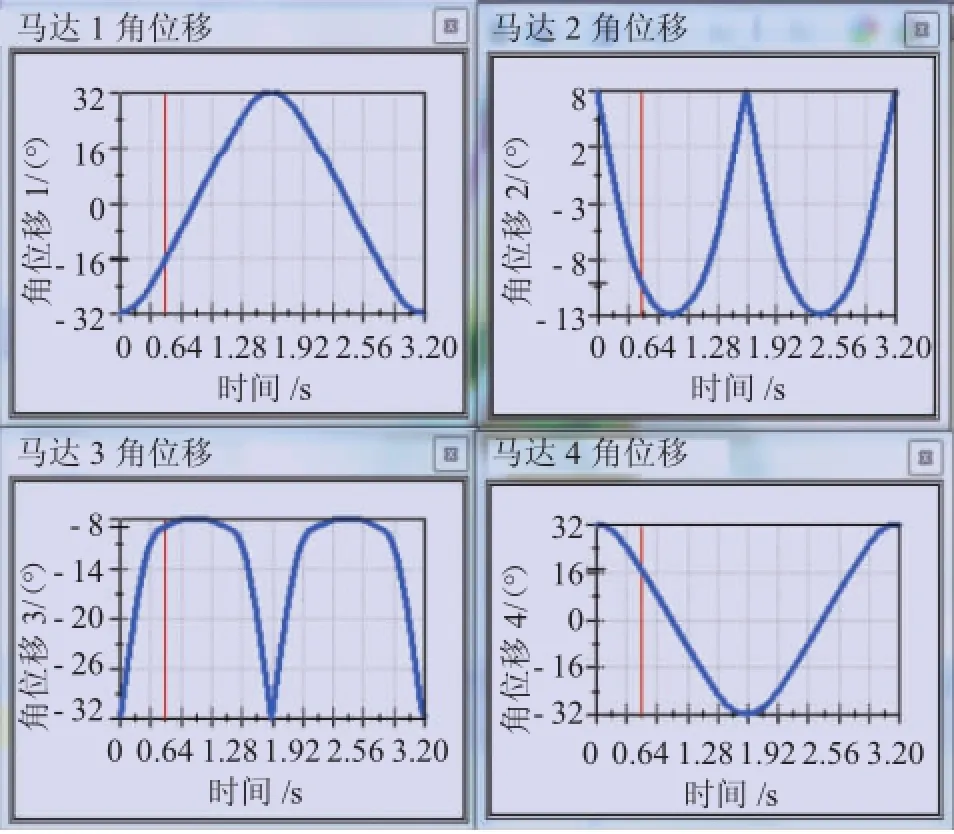
圖6 驅動馬達的角位移曲線
(4)以MATLAB和SolidWorks軟件為工具,通過三維運動仿真,驗證了機器人幾何解法的正確性和有效性。

圖7 碼垛機器人運動仿真末端真實軌跡
[1]游瑋.雙平行四邊形高速重載搬運機器人動態設計與控制研究[D].哈爾濱:哈爾濱工業大學,2011.
[2]王昊杰,薛強.一種三坐標并聯動力頭——Sprint Z3的運動學逆解及尺度綜合 [J].機床與液壓,2011(17):53-56.
[3]黃真.高等空間機構學[M].北京:高等教育出版社,2004.
[4]陸晶,高國琴,朱彩紅,等.新型三平移并聯機構的運動分析和工作空間分析 [J].機械設計與制造,2007(11):163-165.
[5] Li Yangmin,Xu Qingsong.Kinematic Analysis ofa 3-PRS Parallel Manipulator[J].Robotics and Computer Integrated Manufacturing,2007,23(4):395-408.
[6]劉辛軍,汪勁松,李劍鋒,等.一種新型空間3自由度并聯機構的正反解及工作空間分析 [J].機械工程學報,2001(10):36-39.
[7]趙杰,朱延河,蔡鶴皋.Delta型并聯機器人運動學正解幾何解法[J].哈爾濱工業大學學報,2003(1):25-27.
Forward,inverse kinematics of the robot is a bridge to connect control system and mechanical system for robot motion and currently there is no universal solved process for the closed form solution.Although the numerical iterative algorithm of algebraic equations is in common use,however it is difficult to guarantee timeliness and accuracy requirements.By analyzing the mechanical feature of palletizing robot to simplify kinematics model based on the method of geometry,it is possible toderive detailed solving process for the forward and the inverse kinematics.The derivation process is simple and intuitive.Finally the correctness of the Geometric solution is verified by MATLABprogramming and motion simulation of SolidWorks 3-D solid model.
碼垛機器人;幾何解法;正向運動學;逆向運動學
Palletizing Robot;Geometric Solution;Forward Kinematics;Inverse Kinematics
TP242.2
A
1672-0555(2015)04-044-04
*國家科技重大專項(編號:2011ZX04013-011)
2015年8月
郭小寶(1988-),男,碩士,助理工程師,主要從事機器人機構學及其運動控制的研究

