兵馬未動(dòng)，糧草先行

孫衛(wèi)星　尹偉偉

【摘要】高中數(shù)學(xué)中關(guān)于漸近線的知識(shí)，學(xué)生學(xué)習(xí)時(shí)難以體會(huì)曲線漸進(jìn)的方向與方程。幫助學(xué)生領(lǐng)會(huì)“漸近線”的內(nèi)涵并確定漸近線方程，同時(shí)畫出方程的草圖。對(duì)迅速、準(zhǔn)確認(rèn)識(shí)某些函數(shù)的形狀、位置、大小必會(huì)有極大的幫助。同時(shí)能培養(yǎng)了學(xué)生的創(chuàng)新意識(shí)，以及舉一反三的能力。

【關(guān)鍵詞】確定漸近線 數(shù)形結(jié)合

【中圖分類號(hào)】G633.6 【文獻(xiàn)標(biāo)識(shí)碼】A 【文章編號(hào)】2095-3089（2015）08-0029-02

“無(wú)限接近，卻永不相交”，漸近線總讓人覺(jué)得“高冷”，又像哲理一樣令人印象深刻，其實(shí)最早的時(shí)候數(shù)學(xué)和哲學(xué)是不分的。我覺(jué)得這才是數(shù)學(xué)的美，學(xué)習(xí)數(shù)學(xué)的一種樂(lè)趣！

高中數(shù)學(xué)的許多方程圖象和曲線都與漸近線密切相關(guān)，由于學(xué)生在學(xué)習(xí)過(guò)程中不能深刻領(lǐng)會(huì)“漸近線”的內(nèi)涵，，忽視“漸近線”的現(xiàn)象頻頻發(fā)生，導(dǎo)致解題過(guò)程中出現(xiàn)偏差。在涉及漸近線的教學(xué)過(guò)程中，教師要能培養(yǎng)學(xué)生的作圖意識(shí)，要經(jīng)常性地引導(dǎo)學(xué)生根據(jù)方程的漸近線來(lái)畫出方程的草圖，對(duì)迅速找到解決問(wèn)題的入口，為有效地解決問(wèn)題提供幫助。可以說(shuō)漸近線是圖象和曲線的先行者，在圖象中漸近線的定位作用舉足輕重。所以，“兵馬未動(dòng)，糧草先行”，為了作出含有漸近線的比較精確的圖像，必須深度研究函數(shù)的性質(zhì)，求出它的漸近線方程就顯得尤為重要.下面舉例闡述圖象的漸近線的簡(jiǎn)單確定方法，并對(duì)問(wèn)題的處理予以剖析。

一、高中數(shù)學(xué)幾種常見(jiàn)有顯著漸近線的情況

學(xué)習(xí)漸近線的難點(diǎn)在于學(xué)生難以體會(huì)曲線漸進(jìn)的方向與方式，在學(xué)習(xí)過(guò)程中如果能領(lǐng)會(huì)“漸近線”的內(nèi)涵， 對(duì)迅速、準(zhǔn)確認(rèn)識(shí)某些函數(shù)的形狀、位置、大小必會(huì)有極大的幫助，真正體會(huì)“一葉而知秋”的感覺(jué)，從而獲得學(xué)習(xí)數(shù)學(xué)的樂(lè)趣。幫助他們整理幾種常見(jiàn)有顯著漸近線的情況，有助于他們學(xué)習(xí)總結(jié)。

常見(jiàn)的有指數(shù)函數(shù)的漸近線是x軸；對(duì)數(shù)函數(shù)的漸近線是y軸；對(duì)勾函數(shù)的漸近線是x軸、y軸以及y=x；當(dāng)a<0時(shí)冪函數(shù)y=xa的漸近線是x軸、y軸；圓錐曲線雙曲線漸近線公式 的漸近線是等情況。

例1：反比例函數(shù)變式的漸近線方程是。

分析：由題意可得函數(shù)f（x）的圖象與直線y=k有二個(gè)不同的交點(diǎn)，結(jié)合圖象求出實(shí)數(shù)k的取值范圍。

如圖所示：故實(shí)數(shù)k的取值范圍是。

本題主要考查函數(shù)的零點(diǎn)與方程的根的關(guān)系，體現(xiàn)了化歸與轉(zhuǎn)化、數(shù)形結(jié)合的數(shù)學(xué)思想，其中漸近線能否先作出是解題的關(guān)鍵。

二、含有漸近線的分式函數(shù)型、超越函數(shù)型

高中階段很多函數(shù)綜合性問(wèn)題都會(huì)考查到數(shù)形結(jié)合思想，在學(xué)生中流傳著這樣一句話“若要題目不難搞，準(zhǔn)確作圖不可少”，如果能結(jié)合漸近線作出比較精確的函數(shù)圖像，特別是對(duì)稍微復(fù)雜的函數(shù)，領(lǐng)會(huì)它的各種性質(zhì)，則在處理綜合性的問(wèn)題時(shí)才能得心應(yīng)手，游刃有余.比如方程的有解問(wèn)題等。漸近線像人的脊柱那樣對(duì)函數(shù)的圖像進(jìn)行了定位，可謂舉足輕重.有了它，定義域、值域、單調(diào)性才能一目了然。

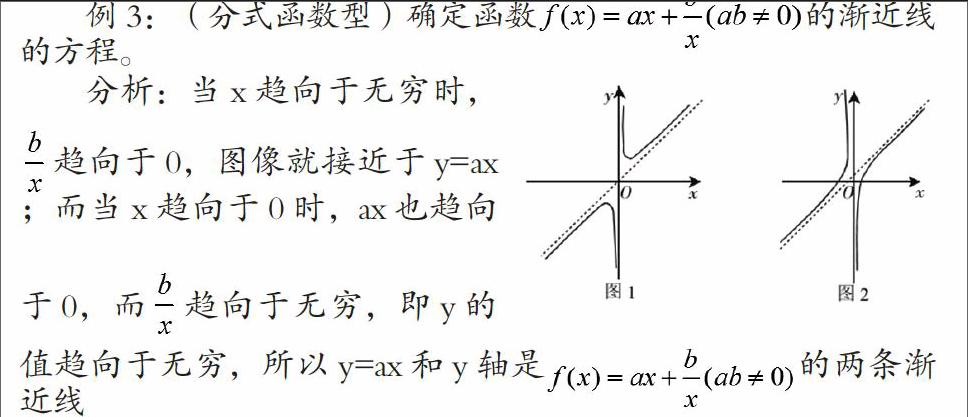
例3：（分式函數(shù)型）確定函數(shù)的漸近線的方程。

分析：當(dāng)x趨向于無(wú)窮時(shí)，趨向于0，圖像就接近于y=ax ；而當(dāng)x趨向于0時(shí)，ax也趨向于0，而趨向于無(wú)窮，即y的值趨向于無(wú)窮，所以y=ax和y軸是的兩條漸近線

如圖1（a>0，b>0）和圖2（a>0，b<0） 。

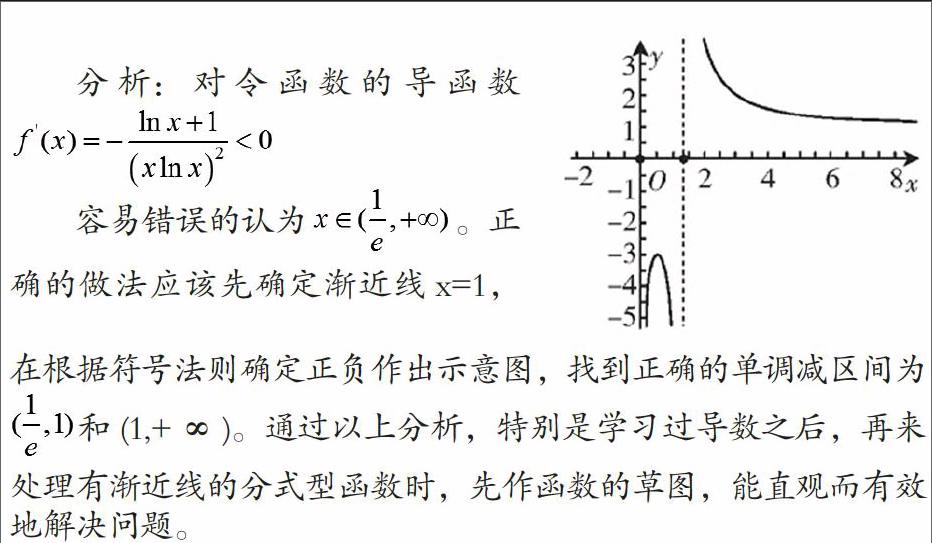
容易錯(cuò)誤的認(rèn)為。正確的做法應(yīng)該先確定漸近線x=1，在根據(jù)符號(hào)法則確定正負(fù)作出示意圖，找到正確的單調(diào)減區(qū)間為和（1，+∞）。通過(guò)以上分析，特別是學(xué)習(xí)過(guò)導(dǎo)數(shù)之后，再來(lái)處理有漸近線的分式型函數(shù)時(shí)，先作函數(shù)的草圖，能直觀而有效地解決問(wèn)題。

本文闡述圖象的漸近線的簡(jiǎn)單確定方法，及漸近線對(duì)函數(shù)的單調(diào)性、值域的影響。老師要能經(jīng)常性地培養(yǎng)學(xué)生的作圖意識(shí)，要經(jīng)常性地引導(dǎo)學(xué)生根據(jù)函數(shù)的各種性質(zhì)特別是函數(shù)的漸近線來(lái)畫出函數(shù)的草圖，對(duì)迅速找到解決問(wèn)題的入口，對(duì)培養(yǎng)學(xué)生形成解決函數(shù)問(wèn)題的大局觀、層次感和養(yǎng)成良好的思維習(xí)慣大有裨益。