考慮不確定復合控制系統(tǒng)動態(tài)特性的前向攔截三維導引律

張友安，吳華麗，梁 勇，張金鵬

（1．海軍航空工程學院控制工程系，山東煙臺264001；2．中國空空導彈研究院，河南洛陽471099；3．航空制導武器航空科技重點實驗室，河南洛陽471099）

考慮不確定復合控制系統(tǒng)動態(tài)特性的前向攔截三維導引律

張友安1，吳華麗1，梁 勇1，張金鵬2，3

（1．海軍航空工程學院控制工程系，山東煙臺264001；2．中國空空導彈研究院，河南洛陽471099；3．航空制導武器航空科技重點實驗室，河南洛陽471099）

為實現(xiàn)高空高速目標的精確攔截，研究了考慮直接力氣動力復合控制動態(tài)特性及不確定性的前向攔截三維導引律設計方法。對采用復合控制的慢旋導彈的動力學模型進行了線性化處理，在氣動舵控制的基礎上設計連續(xù)直接力，然后對其進行離散化處理，避免復雜的控制分配問題。在三維彈目相對運動模型和不確定導彈動力學線性化模型的基礎上，利用時標分離的思想將系統(tǒng)劃分為慢變子系統(tǒng)和快變子系統(tǒng)，應用基于李雅普諾夫穩(wěn)定性理論的魯棒控制方法對慢變子系統(tǒng)和快變子系統(tǒng)分別進行魯棒動態(tài)逆設計，得到考慮不確定復合控制系統(tǒng)動態(tài)特性的前向攔截三維導引律。對單通道控制和雙通道控制的情況分別進行了仿真研究，驗證了本文方法的正確性和有效性。

李雅普諾夫穩(wěn)定性；直接力氣動力復合控制；前向攔截；三維導引律；魯棒動態(tài)逆

0 引 言

按照攔截導彈與目標的相對位置與相對速度的關系，傳統(tǒng)的攔截方式可分為迎頭攔截和尾追攔截。迎頭攔截會使彈目之間的相對運動速度非常大，導致末制導的剩余時間更短，對攔截導彈過載能力的要求就更高；尾追攔截要求導彈的速度大于目標速度，對攔截器的能量設備要求過高而難以實現(xiàn)。因此，文獻［1－2］提出了前向追擊攔截導引方式，建立了二維前向追擊攔截導引運動模型。對于大氣層內使用連續(xù)氣動舵控制的攔截器，在不考慮彈體動態(tài)特性以及過載限制的理想情況下，設計了前向追擊攔截導引律；對于大氣層外的攔截彈，基于噴氣直接力控制設計了Bang－Bang控制導引律。文獻［3］設計了基于變結構控制的前向攔截導引律，分析了導引品質明顯優(yōu)于采用迎頭攔截的導引規(guī)律，但沒有考慮彈體動態(tài)特性的影響。文獻［4－5］建立了目標和攔截器的三維制導模型，設計了三維非線性變結構前向攔截制導律，但是都將導彈視為質點，忽略了彈體的動態(tài)特性。文獻［6－7］將彈體動態(tài)特性用簡單的一階模型來近似，不能反映直接力與氣動力復合控制的特點。文獻［8］通過早期的角度約束，應用滑模變結構控制方法設計了相應的導引律，適用于迎頭攔截、尾追攔截和前向攔截。文獻［9－11］設計了滑模導引律，文獻［12－13］分別利用反饋線性化和動態(tài)逆的方法設計了三維導引律，文獻［14］提出了圓周角導引的新概念，文獻［15］提出了視線導引的方法。

為了更加符合臨近空間攔截高速目標的實際需求，攔截導彈一般會采用直接力／氣動力復合控制的方式［16－18］。文獻［19］在準彈體系下建立模型，對采用直接力氣動力復合控制導彈的控制系統(tǒng)進行了研究，采用擴張狀態(tài)觀測器對不確定性進行處理。文獻［20］分析和簡化了準彈體系下的模型，對采用雙通道控制和單通道控制的姿控發(fā)動機的控制律分別進行了研究，實現(xiàn)了加速度的快速跟蹤。

現(xiàn)有前向攔截導引律設計相關文獻沒有考慮直接力／氣動力復合控制的動態(tài)特性與特點。由于對空中目標的攔截通常是發(fā)生在三維空間的，本文在考慮復合控制動態(tài)特性、特點和不確定性的基礎上，對三維前向攔截導引律進行研究。

1 前向攔截制導數(shù)學模型

前向攔截示意圖如圖1所示［6］，先將攔截導彈引向目標飛行軌道的前方，進而和目標沿同一方向飛行，要求攔截導彈的速度低于目標速度，攔截導彈通過尾部的導引頭探測目標并做出相應的機動，使之始終保持在目標的飛行軌道上，當目標足夠接近時，引爆戰(zhàn)斗部或與之碰撞，徹底摧毀目標。

1．1 相對運動數(shù)學模型

假設導彈和目標的加速度矢量分別與它們各自的速度矢量垂直，即施加在導彈和目標上的加速度矢量僅改變其速度的方向而不改變速度的大小。

三維前向攔截的彈目運動幾何關系如圖2所示［4］，I表示攔截導彈，T表示目標，r表示彈目相對距離。xiyizi是參考坐標系，與各軸對應的單位矢量分別為ii，ji，ki；xLyLzL是視線坐標系，與各軸對應的單位矢量分別為iL，jL，kL；xIyIzI是攔截導彈速度坐標系，與各軸對應的單位矢量分別為iI，jI，kI；xTyTzT是目標速度坐標系，與各軸對應的單位矢量分別為iT，jT，kT。φL和θL是慣性坐標系到視線坐標系轉換的歐拉角，φI和θI是攔截導彈速度坐標系到視線坐標系轉換的歐拉角，φT和θT是目標速度坐標系到視線坐標系轉換的歐拉角。

圖1 前向追擊攔截示意圖

圖2 三維攔截幾何圖

根據(jù)圖2可得到導彈和目標相對運動方程如下：

式中，VI和VT分別表示攔截導彈速度和目標速度和分別為視線角速率沿jL和kL的分量；ayI和azI分別為攔截導彈的俯仰加速度和偏航加速度；ayT和azT分別為目標的俯仰加速度和偏航加速度。

要想前向追擊攔截到目標，在末制導的最后階段，要求目標和攔截導彈的運動方向一致［4］，即

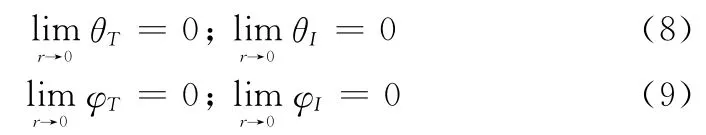
前向攔截導引的目標是把導彈導引到式（8）、式（9）滿足的攔截點，因此，在設計過程中要求θI和θT、φI和φT保持如下比例關系［4］：

式中，N1和N2為導航系數(shù)。

1．2 導彈動力學模型

為了充分利用側噴發(fā)動機，攔截導彈需要以一定的速度旋轉，因此在準彈體系建立滾轉導彈動力學模型［21］，如圖3所示［19］，脈沖發(fā)動機是交錯分布的，一共有10圈，每圈18個發(fā)動機。

圖3 姿控式復合控制自旋導彈配置示意圖

假設彈體是軸對稱形式并以一定角速度慢旋，導彈動力學模型為

其中

式中，M為攔截導彈質量；α為準彈體系下的攻角；β為準彈體系下的側滑角；u、v、w分別為VI在準彈體系各軸的分量；Ix、Iy、Iz分別為在各軸方向轉動慣量的分量；ωz、ωy、ωx分別為導彈角速度在準彈體系的分量；?為俯仰角；Ty、Tz和NT、MT分別為直接側向力和力矩在準彈體系的分量；KTy、KTz和KM、KN分別為噴流干擾力和干擾力矩放大因子；Ng、Mg為馬格努斯力矩；Yα、Yδe、Zβ、Zδr、Nβ、Nr、Nδr、Mα、Mq、Mδe為動力學導數(shù)；ΔYα、ΔYδe、ΔZβ、ΔZδr、ΔNβ、ΔNr、ΔNδr、ΔMα、ΔMq、ΔMδe為動力學導數(shù)攝動；δe、δr為舵偏角在準彈體系的分量。

2 復合控制策略

采用直接力／氣動力復合控制導彈的控制策略是在氣動舵控制的基礎上，先假設直接力是連續(xù)的并進行控制設計，然后對其進行離散化處理，得到離散直接力控制。

為簡化控制設計，采用小角度線性化的思想，即假設α和β都是小角度，則式（12）～式（15）可轉換為

其中

攔截導彈控制系統(tǒng)通常采用過載控制，加速度和角速度易于測量，而攻角α和側滑角β一般難于測量。為了避免復合控制律中出現(xiàn)α和β，利用

進行變換，并且假設氣動舵采用如下控制規(guī)律（忽略舵機的動態(tài)）：

得到含有氣動舵反饋控制在內的導彈動力學模型

為簡化控制設計，式（20）只考慮了氣動力產生的過載，忽略了直接力和舵的影響。

假設俯仰通道和偏航通道的直接力是連續(xù)的，與舵控制系統(tǒng)類似，分別為T′y和T′z，控制規(guī)律取為

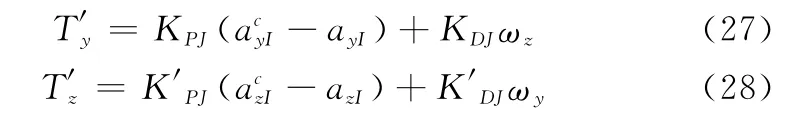
式中，KPJ、K′PJ和KDJ、K′DJ是比例系數(shù)和反饋系數(shù)。

式（27）、式（28）表示的直接力是連續(xù)信號，而實際的直接力是離散脈沖信號，需將連續(xù)直接力信號T′y和T′z進行離散化等效處理，得到可以實施的直接力信號Ty和Tz。

3 導引律設計

為了簡化導引律的設計，將攔截導彈和目標的質點運動學與加速度動力學構成的動態(tài)系統(tǒng)，看成慢變子系統(tǒng)，將角速度動態(tài)子系統(tǒng)看成快變子系統(tǒng)。

3．1 慢變動力學的魯棒動態(tài)逆設計

定義變量

式中，τi（i＝1，2）為比例系數(shù)，反映了當s1i＝0時ei→0的快慢程度，且

由式（29）知

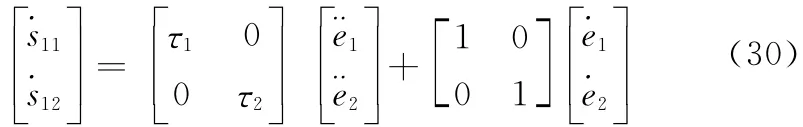
式中

其中

容易得到Δf1i（i＝1，2）的界為

式中，d為氣動參數(shù)的最大不確定性程度，其取值范圍是0＜d＜1；d11和d12為很小的正數(shù)。進一步可以求出˙ρ11、˙ρ12。

取動態(tài)逆控制律為

式中，k11、k12為慢變動力學子系統(tǒng)的帶寬。取魯棒控制項為

式中，ε1i為小的正數(shù)。

取慢變動力學子系統(tǒng)的李雅普諾夫函數(shù)為

利用不等式［22］

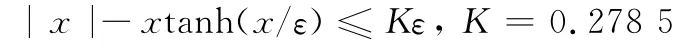
可以證明

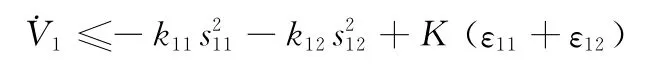
因此，慢變子系統(tǒng)是有界穩(wěn)定的，適當選取k11、k12和ε11、ε12的值，可使s11、s12達到要求的精度。

式（33）為慢變動力學子系統(tǒng)的魯棒動態(tài)逆控制律，其計算需要用到式（34）。

3．2 快變動力學的魯棒動態(tài)逆設計

快變動力學子系統(tǒng)可寫為

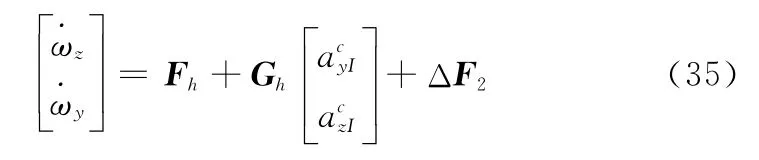
式中

其中

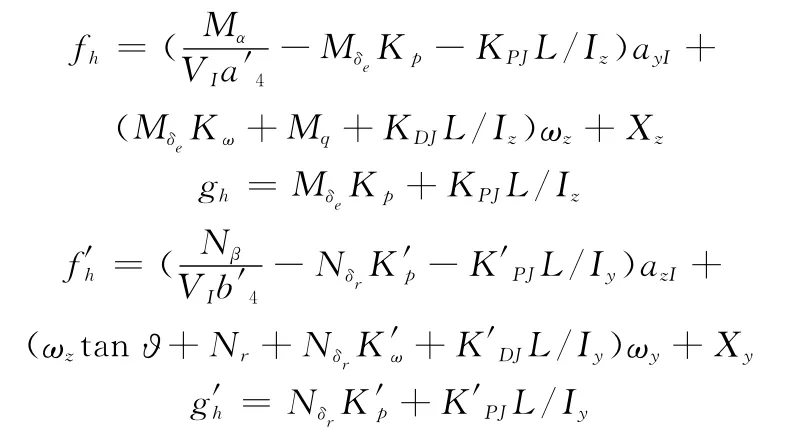
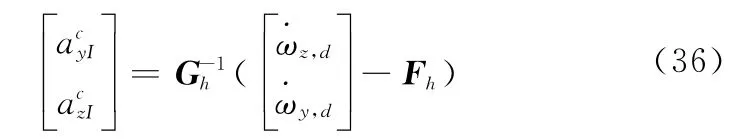
將式（36）代入式（35），得

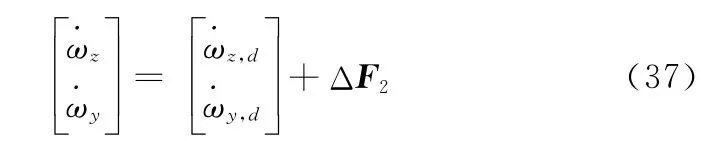
可以求得Δf2i（i＝1，2）的界為

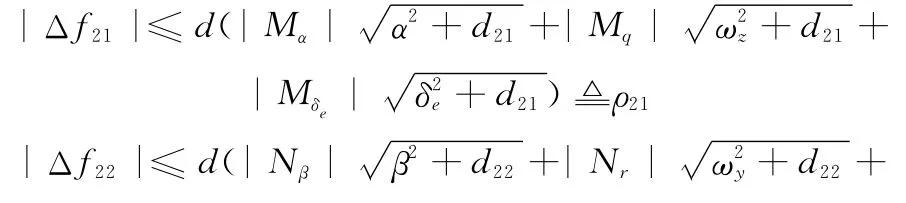
式中，d21和d22為很小的正數(shù)。

取快變動力學子系統(tǒng)的李雅普諾夫函數(shù)為

式中

選取快變動力學子系統(tǒng)的魯棒控制律為

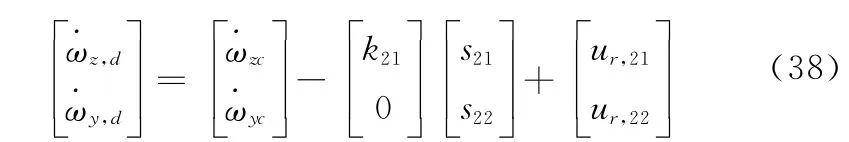
式中，k21、k22為快變動力學子系統(tǒng)的帶寬。取魯棒控制項為

可以證明

因此，快變動力學子系統(tǒng)是有界穩(wěn)定的，適當選取k21、k22和ε21、ε22的值，可使s21和s22達到要求的精度。

式（36）為考慮復合控制系統(tǒng)動態(tài)特性和不確定性的前向攔截導引律，其計算需要用到式（38）、式（39）。

與二維平面情況不同的是，在三維空間情況下，有兩種直接力控制方式可供選擇：一種方式是同時對俯仰和偏航兩個通道分別進行控制，即所謂的雙通道控制方式，直接側向力可通過將式（27）、式（28）離散化得到；另外一種方式是將俯仰和偏航兩個通道的力合成后，采用單通道矢量控制方式。

將T′y和T′z合成，得到連續(xù)的合力為

通過將P′進行離散化，得到離散直接力P。P與俯仰方向夾角為φ，定義如下：

式中，ε為一比較小的正數(shù)，當｜T′y｜＜ε時，則不用計算φ。

采用單通道控制時，考慮發(fā)動機側噴的實際情況（彈體滾轉和側噴發(fā)動機的個數(shù)限制），某一周期當所需側噴的方向上已沒有側噴發(fā)動機可用時，則不側噴，等待下一個周期。

4 仿真驗證

為驗證方法的有效性進行如下仿真，假設在高空導彈能夠產生的最大過載為4 g。目標的信息可以通過觀測器、濾波等手段得到，這里假設目標的信息精確已知。

設目標速度為2 100m／s，某型攔截導彈的飛行速度為1 500m／s，彈體自旋速度為2．22πrad／s，導彈質量為140kg，轉動慣量Iz＝Iy＝200kg·m2，Ix＝180kg·m2，每個脈沖發(fā)動機的標稱推力為2 000N，工作周期T＝0．025s。

取氣動系數(shù)Yα＝4．192 5，Yδe＝1．5，Mα＝0．514 8，Mq＝－0．025 7，Mδe＝－8．083 5，Zβ＝－0．027 9，Zδr＝0．01，Nβ＝0．514 8，Nr＝－0．025 7，Nδr＝－8．083 5。

為簡單起見，這里取固定的Kp、Kω、KPJ、KDJ、K′p、K′ω值，即Kp＝－0．003 9，Kω＝0．160 4，K′p＝－0．003 9，K′ω＝

0．160 4，KPJ＝0．035，KDJ＝－0．315，K′PJ＝0．035，K′DJ＝－0．315。

假設噴流干擾力放大因子KTy＝KTz＝0．2，噴流干擾力矩放大因子KM＝KN＝0．3，氣動參數(shù)向下拉偏40%。

目標初始位置為（－9 800m，36 000m，0m），攔截導彈初始位置為（9 000m，28 000m，1 000m），且θT、θI、φT、φI的初值分別是14°、35．5°、6°和18°。τ1＝τ2＝0．6，為確保直接力／氣動力復合控制系統(tǒng)加速度慢變狀態(tài)與角速度快變狀態(tài)可分離，k11＝k12＝0．4，k21＝k22＝4，n1＝n2＝3。

實際工程應用時，可針對不同的特征點分別進行設計，然后進行插值處理。

對于采用單通道控制的攔截導彈，部分仿真結果如圖4所示。圖4（a）為θT和θI的變化曲線，圖4（b）為φT和φI的變化曲線，它們全部單調收斂到0，滿足式（8）、式（9）給出的前向攔截條件，保證了攔截導彈能夠準確地攔截到目標。圖4（c）反映了攔截導彈側噴發(fā)動機的消耗情況，共消耗了90個。圖4（d）為舵偏角變化曲線，當側噴發(fā)動機工作時，舵偏角比較大。圖4（e）為攔截導彈的攻角和側滑角，直接力可以迅速建立起攻角和側滑角。圖4（f）為彈目運動軌跡，攔截導彈逐漸地運動到目標的前方，直到最后摧毀目標。

圖4 單通道控制仿真結果

對于采用雙通道控制的攔截導彈，部分仿真結果如圖5所示。同雙通道控制相比，控制效果比較相近。但是，采用雙通道控制，俯仰通道發(fā)動機側噴38個，偏航通道發(fā)動機側噴76個，可見，采用單通道控制方式可以有效減少側噴發(fā)動機的消耗。

如果不引入直接力控制，單純采用氣動舵進行控制，由于攔截導彈的過載響應比較緩慢，攔截導彈將無法命中目標，限于篇幅，不再給出仿真曲線。

圖5 雙通道控制仿真結果

5 結 論

對于采用直接力／氣動力復合控制的導彈，為了充分利用側噴發(fā)動機，導彈需要以一定的速度自旋，因此在準彈體系下建立導彈動力學模型進行研究。對動力學模型進行了線性化處理，在氣動舵控制的基礎上設計連續(xù)直接力，然后對其進行離散化處理，避免復雜的控制分配問題，便于前向攔截導引律設計時考慮復合控制的動態(tài)特性和特點。

對慢變動力學子系統(tǒng)和快變動力學子系統(tǒng)分別進行動態(tài)逆設計，應用李雅普諾夫穩(wěn)定性理論的魯棒控制方法對系統(tǒng)的不確定性進行處理，得到考慮復合控制系統(tǒng)動態(tài)特性及其不確定性的前向攔截三維導引律。

在考慮過載限制、氣動參數(shù)的不確定性和噴流干擾的情況下對單通道控制和雙通道控制分別進行了仿真研究。結果表明，直接側向力能夠迅速建立起攻角和側滑角，所設計的導引律能夠保證攔截導彈準確命中目標，并且，采用單通道控制方式可以有效減少發(fā)動機的消耗。如果單純采用氣動舵進行控制，所設計的導引律無法保證攔截導彈命中目標。說明了所設計導引律的正確性和魯棒性。

［1］Golan O M，Shima T．Head pursuit guidance for hypervelocity interception［C］∥Proc．of the AIAA Guidance，Navigation and Control Conference and Exhibit，2004．

［2］Golan O M，Shima T．Precursor interceptor guidance using the sliding mode approach［C］∥Proc．of the AIAA Guidance，Navigation and Control Conference，2005．

［3］Zhao Z H，Shen Y，Liu H．A head pursuit guidance schemebased on variable structure control［J］．Journal of Astronautics，2007，28（4）：835－839．（趙振昊，沈毅，劉鶴．基于變結構控制的前向攔截導引方法［J］．宇航學報，2007，28（4）：835－839．）

［4］Ge L Z，Shen Y，Yuan L H．Three－dimensional guidance model and guidance law design for head pursuit interception［J］．Systems Engineering and Electronics，2008，30（6）：1118－1121．（葛連正，沈毅，院老虎．前向攔截的三維制導模型及制導律設計［J］．系統(tǒng)工程與電子技術，2008，30（6）：1118－1121．）

［5］Ge L Z，Shen Y．Head pursuit variable structure guidance law for three－dimensional space interception［J］．Chinese Journal of Aeronautics，2008，21（3）：247－251．

［6］Shima T．Head pursuit guidance［J］．Journal of Guidance，Control and Dynamics，2007，30（5）：1437－1444．

［7］Taub I，Shima T．Intercept angle missile guidance under timevarying acceleration bounds［J］．Journal of Guidance Control and Dynamics，2013，36（3）：686－699．

［8］Shima T．Intercept－angle guidance［J］．Journal of Guidance Control and Dynamics，2011，34（2）：484－492．

［9］Lum K Y，Xu J X，Abidi K．Sliding mode guidance law for delayed LOS rate measurement［C］∥Proc．of the AIAA Guidance，Navigation and Control Conference，2008．

［10］Shima T，Idan M，Golan O M．Sliding－mode control for integrated missile autopilot guidance［J］．Journal of Guidance，Control and Dynamics，2006，29（2）：250－260．

［11］Idan M，Shima T，Golan O M．Integrated sliding mode autopilot－guidance for dual－control missiles［J］．Journal of Guidance，Control and Dynamics，2007，30（4）：1081－1090．

［12］Srivastava R，Sarkar A K，Ghose D，et al．Nonlinear three dimensional composite guidance law based on feedback linearization［C］∥Proc．of the AIAA Guidance，Navigation and Control Conference，2004．

［13］Srivastava R，Prabhakar N，Sarkar A K，et al．Three dimensional nonlinear inverse dynamics guidance law for parallel navigation［C］∥Proc．of the AIAA Guidance，Navigation and Control Conference，2004．

［14］Tsalik R，Shima T．Inscribed angle guidance［C］∥Proc．of the AIAA Guidance，Navigation and Control Conference，2013．

［15］Ratnoo A，Shima T．Line－of－sight interceptor guidance for defending an aircraft［J］．Journal of Guidance，Control and Dynamics，2011，34（2）：522－532．

［16］Zimpfer D J，Shieh L S，Sunkel J．Redesigned pulse－widthmodulation spacecraft control［J］．Journal of Guidance，Control and Dynamics，1998，21（4）：529－534．

［17］Bernelli Z F，Mantegazza P，Nurzia V．Multi－pulse－width modulated control of linear systems［J］．Journal of Guidance，Control and Dynamics，1998，21（1）：64－70．

［18］Doman D B，Gamble B J，Ngo A D．Control allocation of reaction control jets and aerodynamic surfaces for entry vehicles［C］∥Proc．of the AIAA Guidance，Navigation and Control Conference，2007．

［19］Yao Y，Bi Y T．Design of blended control strategy for missiles with lateral jets and aerodynamic surfaces［J］．Acta Aeronautica et Astronautica Sinica，2010，31（4）：701－707．（姚郁，畢永濤．姿控式直接側向力與氣動力復合控制策略設計［J］．航空學報，2010，31（4）：701－707．）

［20］Ma K M，He F H．Control law design of lateral attitude jets for spinning missile［J］．Acta Aeronautica et Astronautica Sinica，2009，30（10）：1816－1822．（馬克茂，賀風華．彈體自旋條件下姿控發(fā)動機控制律設計［J］航空學報，2009，30（10）：1816－1822．）

［21］Qian X F，Lin R X，Zhao Y N．Missile flight dynamics［M］．Beijing：Beijing Institute of Technology Press，2003．（錢杏芳，林瑞雄，趙亞男．導彈飛行力學［M］．北京：北京理工大學出版社，2003．）

［22］Polycarpou M M．Stable adaptive neural network control scheme for nonlinear systems［J］．IEEE Trans．on Automatic Control，1996，41：447－451．

E－mail：zhangya63＠sina．com

吳華麗（1980－），通信作者，女，講師，博士研究生，主要研究方向為導彈制導與控制。

E－mail：whl＿yy＠126．com

梁 勇（1976－），男，副教授，博士，主要研究方向為導彈制導與控制。E－mail：ytliangyong＠sina．com

張金鵬（1964－），男，研究員，博士，主要研究方向為制導控制技術。E－mail：apeng－zhang＠163．com

Three－dimensional head pursuit guidance law considering dynamic characteristics of uncertain hybrid control system

ZHANG You－an1，WU Hua－li1，LIANG Yong1，ZHANG Jin－peng2，3
（1．Department of Control Engineering，Naval Aeronautical and Astronautical University，Yantai 264001，China；2．China Airborne Missile Academy，Luoyang 471099，China；3．Luoyang Electro－Optics Technology Development Center，Luoyang 471099，China）

In order to intercept targets with high speed in high altitude accurately，a three－dimensional head pursuit guidance law considering uncertain dynamic characteristics for missiles with blended lateral jets and aerodynamic control is researched．The dynamics model of rotating missiles with blended lateral jets and aerodynamic control is simplified by linearization，and based on aerodynamic control，continuous lateral jets control is designed，and then it is discretized，which avoids the complicated control allocation problem．According to the kinematic model of three－dimensional head pursuit guidance and the dynamics linear model with uncertainties of missiles，the system is separated into a slow subsystem and a fast subsystem using time－scale separation，and the robust dynamic inversion controls of the slow subsystem and the fast subsystem are designed separately by applying the robust control method based on the Lyapunov stability theory．Thus，the three－dimensional head pursuit guidance law considering dynamic characteristics of the uncertain hybrid control system is obtained．The simulation of single channel control and double channels control are done to show the accuracy and effectiveness of the proposed method．

Lyapunov stability；blended lateral jets and aerodynamic control；head pursuit；three－dimensional guidance law；robust dynamic inversion

V 448．23

A

10．3969／j．issn．1001－506X．2015．06．20

張友安（1963－），男，教授，博士，主要研究方向為導彈制導與控制、先進控制理論。

1001－506X（2015）06－1354－08

2014－08－07；

2014－11－05；網絡優(yōu)先出版日期：2014－11－20。

網絡優(yōu)先出版地址：http：／／www．cnki．net／kcms／detail／11．2422．TN．20141120．2108．007．html

航空科學基金（20120184001）資助課題