面向任務性目標的裝備狀態(tài)維修決策方法

王少華，張耀輝，韓小孩

（裝甲兵工程學院技術保障工程系，北京100072）

面向任務性目標的裝備狀態(tài)維修決策方法

王少華，張耀輝，韓小孩

（裝甲兵工程學院技術保障工程系，北京100072）

針對定期維修存在的缺點，提出以威布爾比例風險模型（Weibull proportional hazards model，WPHM）作為狀態(tài)描述模型，對裝備進行基于狀態(tài)的維修決策。針對裝備的獨特任務屬性，通過構造決策目標函數(shù)對狀態(tài)維修行為和狀態(tài)檢測間隔期兩類決策內容進行了研究。以轉移概率的形式描述了狀態(tài)協(xié)變量的劣化過程，以條件可用度最大化為目標提出了預防性維修和變步長檢測的狀態(tài)維修決策模型以及計算方法。最后，以某型發(fā)動機為例，對決策方法的適用性和合理性進行了驗證。

狀態(tài)維修決策；比例風險模型；狀態(tài)協(xié)變量；檢測間隔期

0 引 言

狀態(tài)維修是在裝備運行過程中，通過機內或外部檢測設備獲得裝備的狀態(tài)信息，通過狀態(tài)評估和預測得到裝備的實時狀態(tài)和發(fā)展趨勢，并適時安排預防性維修的一種維修方式［1］。狀態(tài)維修的目的是有效地降低故障風險，降低裝備的壽命周期費用，而能否及時、有效地進行維修決策是影響狀態(tài)維修效果的關鍵，因此狀態(tài)維修決策成為了狀態(tài)維修的焦點［2］。

對狀態(tài)維修決策的研究主要包括維修行為決策和檢測間隔期決策。對于維修行為決策來說，如何在延長運行時間所帶來的收益和隨之而來的故障風險之間進行合理的權衡，是研究者關注的重點。對于檢測間隔期決策來說，決策者需要對狀態(tài)檢測信息的效用與狀態(tài)檢測成本進行權衡，對如何實施高效的狀態(tài)檢測進行分析和研究。

目前，在狀態(tài)維修決策方面已經有可觀的研究成果，文獻［3］基于多狀態(tài)假設，分別針對費用目標和可用度目標，對狀態(tài)報警閾值、預防更換閾值和狀態(tài)檢測間隔期的優(yōu)化決策方法進行了研究；文獻［4］將等間隔檢測條件下的狀態(tài)劣化過程視為馬爾可夫隨機過程，以可用度為目標對預防維修閾值和狀態(tài)檢測間隔期的優(yōu)化方法進行了研究；文獻［5］運用時間延遲模型描述狀態(tài)劣化規(guī)律，并在檢測不完全的假設條件下，對燃氣輪機狀態(tài)檢測間隔優(yōu)化方法進行了研究；文獻［6］將狀態(tài)劣化過程視為一類隱馬爾可夫過程，運用比例風險模型對基于狀態(tài)的預防性更換策略進行了研究；文獻［7］提出了基于仿真的預防性維修決策以及檢測間隔期的序貫決策算法。對于具有較強任務屬性的軍事裝備來說，如何減少不必要的狀態(tài)檢測，提高裝備可用度是決策者關注的重點［8］，而文獻［3－7］并未引入狀態(tài)檢測所帶來的經濟和時間成本，無法準確衡量狀態(tài)檢測對裝備可用度的影響并制定相應的決策策略。針對這一情況，本文從提高裝備可用度的角度出發(fā)，對裝備狀態(tài)維修決策方法進行研究。

1 基于狀態(tài)的維修行為決策模型

振動、油液等狀態(tài)檢測信息能夠以相應特征參數(shù)的觀測值反映裝備故障風險的相對大小，因此許多研究者直接以其作為控制參數(shù)，為其制定閾值來進行維修決策，實際上這類信息無法反映裝備故障風險隨役齡增長而呈現(xiàn)出的一致性規(guī)律，一定程度上影響了模型的準確性。針對這一情況，本文采用比例風險模型［9－10］（proportional hzards model，PHM）進行可靠性建模，該模型能夠將役齡與狀態(tài)參數(shù)中包含的信息進行結合來構造可靠度模型，從而更準確地描述裝備的狀態(tài)劣化規(guī)律。

1．1 威布爾比例風險模型

常用的比例風險函數(shù)為指數(shù)型函數(shù)

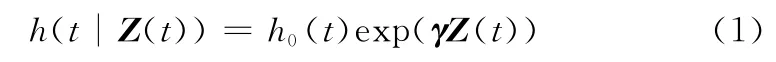
式中，h（t｜Z（t））為風險函數(shù)；h0（t）為基本風險函數(shù)；exp（γZ（t））為協(xié)變量函數(shù)，Z（t）可表示為向量以代表多個協(xié)變量參數(shù)，γ為Z（t）的系數(shù)向量，振動、油液等參數(shù)即可作為協(xié)變量來描述裝備故障風險。由于威布爾函數(shù)能夠較好地描述機械、電氣等裝備關鍵部件的壽命分布規(guī)律，因此以威布爾函數(shù)作為基本風險函數(shù)構造威布爾比例風險模型［11］（Weibull proportional hazards model，WPHM），其形式為

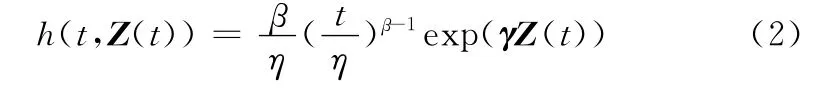
式中，β和η分別為威布爾函數(shù)的形狀參數(shù)和尺度參數(shù)；γ為協(xié)變量Z（t）的系數(shù)［12］。

1．2 協(xié)變量狀態(tài)轉移假設

制定狀態(tài)維修策略的目的是以較大的概率預防故障停機事件的發(fā)生，因此需要對裝備協(xié)變量隨役齡的統(tǒng)計規(guī)律進行分析，以求得維修決策閾值的解析解。首先假定Z（t）僅在有限的狀態(tài)空間S＝｛1，2，…，m｝取值，并且裝備初始狀態(tài)是完好的。在裝備壽命過程中以Δ為間隔對其狀態(tài)進行定期檢測，有Z（kΔ）∈｛1，2，…，m｝（k＝0，1，2，…）。同時假設Z（t）在檢測間隔內保持不變，僅在檢測時刻單調階躍，則有｛Z（t）＝Z（kΔ）｜kΔ≤t＜（k＋1）Δ，k＝0，1，2，…｝，如圖1所示。

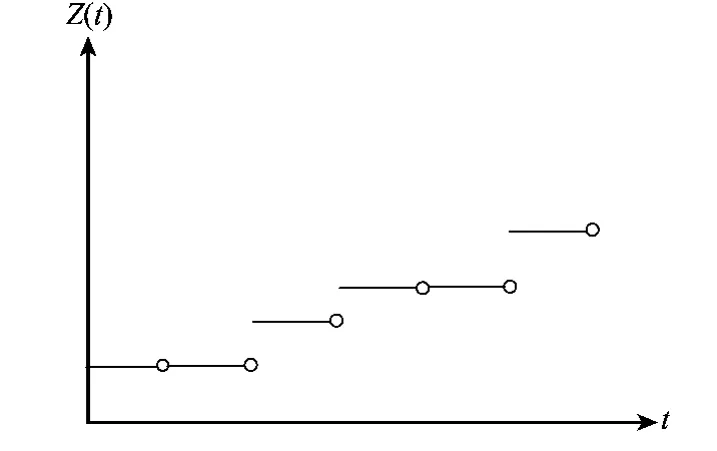
圖1 協(xié)變量Z（t）的右階躍過程

這里以轉移概率的形式表示狀態(tài)協(xié)變量的隨機變化規(guī)律，將協(xié)變量的狀態(tài)轉移概率表示為矩陣P（k），P（k）中的元素piv（k）＝P（Z（（k＋1）Δ）＝v｜T＞（k＋1）Δ，Z（kΔ）＝i），其中T表示裝備壽命。利用被試裝備的狀態(tài)觀測歷史，可以采用極大似然估計法求得P（k）進行估計。

通過參數(shù)估計得到h（t｜Z（t））和P（k）的表達式，即可利用已知信息預測裝備未來的故障風險，并結合決策目標函數(shù)對潛在損失進行定量計算，為維修決策優(yōu)化提供依據(jù)。

1．3 狀態(tài)維修行為決策閾值優(yōu)化

對于系統(tǒng)層次的裝備來說，其可用壽命只有通過更換才能得到恢復，因此裝備從新投入使用到完成下一次更換可視為一個壽命周期。假設裝備在壽命周期內發(fā)生的可修復故障都進行最小維修，最小維修的時間和費用忽略不計，狀態(tài)維修僅針對“狀態(tài)劣化”這一隱蔽故障模式，則狀態(tài)維修決策主要是指如何實施狀態(tài)檢測，如何依據(jù)裝備狀態(tài)檢測信息對是否實施預防性更換進行決策。

為了簡化問題的難度，首先在定期檢測的假設條件下，對預防性更換閾值優(yōu)化方法進行研究。理論上預防性更換應隨時實施，但考慮到實際情況，這里將維修行為策略簡化為：只在離散的檢測時刻決定是否立即實施預防性更換，若在預防性更換前發(fā)生失效，則立即實施更換。

假設裝備預防性更換所需的時間比故障更換低，即預防性更換對于提高裝備可用度是有效的。這里令tp表示單次預防性更換的時間，tf表示由故障更換引起的額外維修時間，tf＞0，則單次故障更換時間為tp＋tf。

以裝備的可用度閾值a為決策變量，在給定a的條件下，可確定相應的預防性更換時間，計算可達可用度φ（a），因此通過改變a的取值，可使裝備的可用度φ（a）達到最大化。

根據(jù)更新理論，在定期檢測條件下，裝備的可達可用度φ（a）［13］可表示為

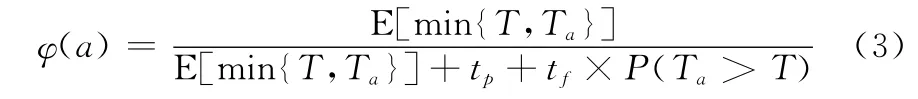
式中，P（Ta＞T）表示在可用度閾值為a的條件下，裝備發(fā)生故障更換的概率；E［min｛T，Ta｝］則表示裝備壽命周期的期望值。

根據(jù)第1．2節(jié)提出的協(xié)變量階躍假設，可以證明當φ（a）＝a時，φ（a）可達到最大值（φ（a）即為目標函數(shù)），相應的a即為最優(yōu)閾值a＊，對應的Ta則為最優(yōu)預防性維修時間［14］。a＊可以通過下列迭代式進行近似求解：

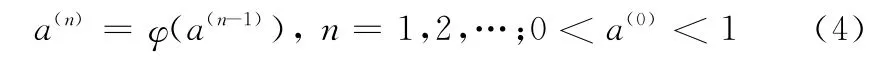
由于狀態(tài)維修決策僅在檢測時刻進行，因此Ta可表示為Δ的整數(shù)倍，在給定閾值a的條件下，對于有限的協(xié)變量等級i∈｛1，2，…，m｝，可以求得對應的更換停止集ki作為預防性更換的依據(jù)［15］

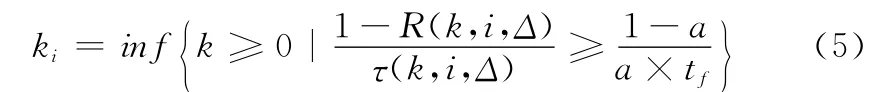
其中

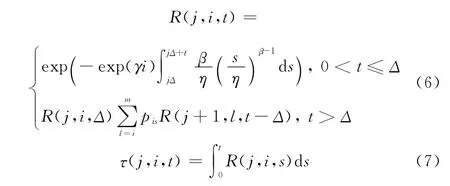
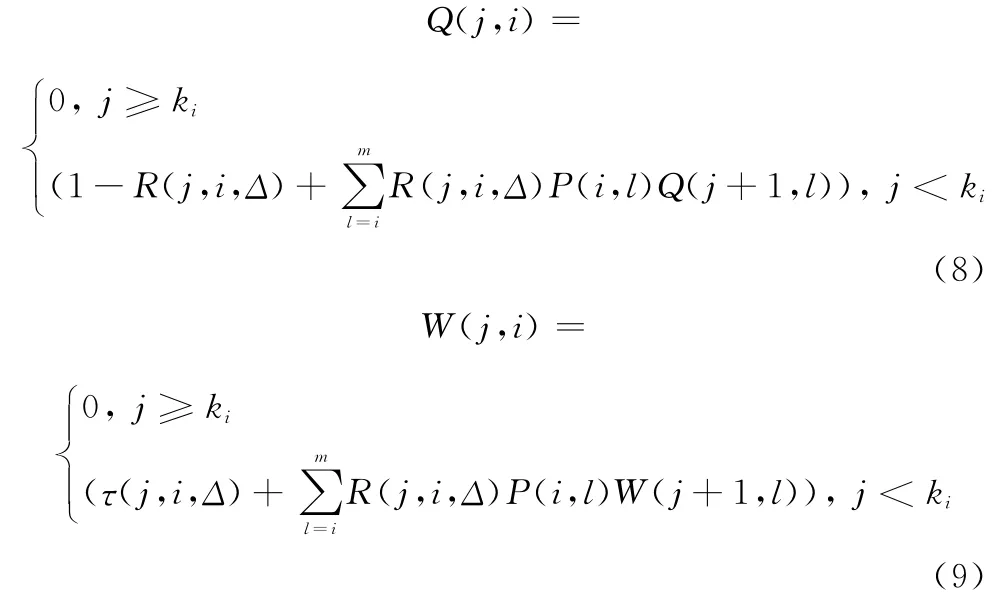
ki與狀態(tài)等級i相對應，若在某時刻觀測到Z（t）＝i，且t＜kiΔ，則可繼續(xù)運行；若kiΔ時刻裝備未失效，且觀測到Z（kiΔ）≥i，應立即進行預防性更換。經計算求得ki后，即可對式（3）中的P（Ta＞T）和E［min｛T，Ta｝］進行求解。

在定期檢測的條件下，P（Ta＞T）和E［min｛T，Ta｝］需要考慮狀態(tài)觀測事件的發(fā)生概率，因此構造迭代函數(shù)Q（j，i）和W（j，i）。其中j表示當期時刻，i表示當期協(xié)變量。則Q（j，i）表示已知Z（jΔ）＝i的條件下，裝備在預防性更換前失效的概率，W（j，i）表示在已知Z（jΔ）＝i的條件下，裝備在預防性更換前的期望剩余壽命。

根據(jù)初始狀態(tài)完好的假設，有Z（0）＝1，則按照上述定義，P（Ta＞T）可表示為Q（0，1），而E［min｛T，Ta｝］可表示為W（0，1），對應的迭代式分別為

首先在（0，1）區(qū)間內為a賦一初值，然后利用式（3）～式（9）進行迭代求解，可以求得最優(yōu)可用度閾值a＊。利用式（5）可求得與a＊對應的停止集ki作為最優(yōu)預防性更換時機。

在裝備運行過程中，假設在t時刻觀測到Z（t）＝i，若t＜kiΔ，則不做任何維修，繼續(xù)運行；若t≥kiΔ，則立即進行預防性更換。

2 狀態(tài)檢測間隔期決策

在等間隔檢測條件下，決策者需要在Δ，2Δ，…等時刻對Z（t）進行觀測，判斷式（4）中的判別式是否成立，從而對是否進行預防性更換進行決策。但實際上，裝備的可靠度在壽命早期往往較高，以Δ為間隔對其狀態(tài)進行定期檢測往往無法發(fā)現(xiàn)明顯的劣化趨勢，隨著役齡的增加，裝備狀態(tài)的劣化及可靠性的降低將日趨顯著，此時相應地縮短檢測間隔，既可為狀態(tài)維修決策提供足夠的信息支撐又能夠減少狀態(tài)檢測對裝備動用的不利影響。依據(jù)這一規(guī)律，本文提出對狀態(tài)檢測間隔期進行序貫的動態(tài)決策，即以Δ為單元在壽命初期采用較長的步長，隨著役齡的增長和狀態(tài)的劣化，逐漸縮短檢測間隔，以減少不必要的檢測，如圖2所示。

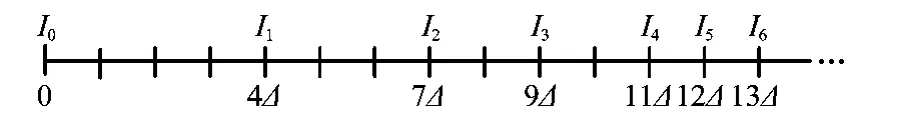
圖2 變步長狀態(tài)檢測策略

該檢測策略是一類前饋決策過程，即隨著裝備狀態(tài)檢測的進行，下一個最佳的狀態(tài)檢測時刻是由當前役齡及狀態(tài)決定的，本文以條件期望可用度最高為決策目標對最優(yōu)狀態(tài)檢測間隔期進行序貫決策。假定當前時刻為τΔ，則依據(jù)式（5）可以得到當期檢測間隔的可行解為

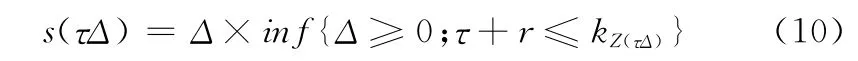
式中，kZ（τΔ）表示協(xié)變量為Z（τΔ）時，對應的預防性更換時刻。

在未來檢測時刻未知的情況下，無法對當期最佳檢測時刻進行求解，因此假定在完成下一檢測之后即按照最小檢測間隔實施序貫檢測。按照該策略可以得到與各可行解相對應的期望可用度，與最大可用度對應的解即為當期檢測間隔。按照上述求解方法可以依據(jù)當期狀態(tài)，序貫地對檢測間隔期進行最優(yōu)決策。

圖3所示為役齡為0時，可行的當期檢測間隔以及對應的序貫實施過程。如圖所示，在0時刻，裝備的狀態(tài)為1，表示裝備處于完好狀態(tài)，首次狀態(tài)檢測時刻I1的可行解為Δ，2Δ，…，k1Δ，依次計算對應的條件可用度，可求得I1的最優(yōu)值。假定I1的最優(yōu)值已確定，則序貫地對I2，I3，…進行決策。以I2為例，Z（I1）可能為｛1，2，…，m｝中的任一值，因此當Z（I1）取值不同時，I2將在不同的時刻取得最優(yōu)解。令τ＝I1，則依據(jù)式（10）可求得I2的可行解范圍，按照圖4所示的狀態(tài)檢測策略，可計算并求得I2的最佳值。

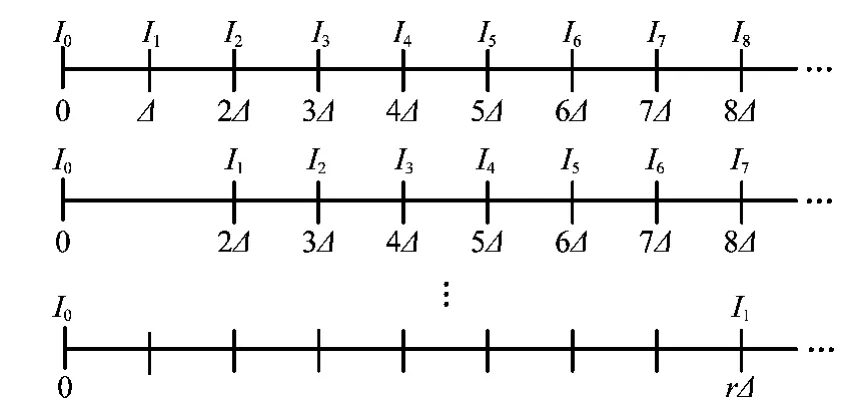
圖3 可行的狀態(tài)檢測間隔（τ＝0；Z（0）＝1）

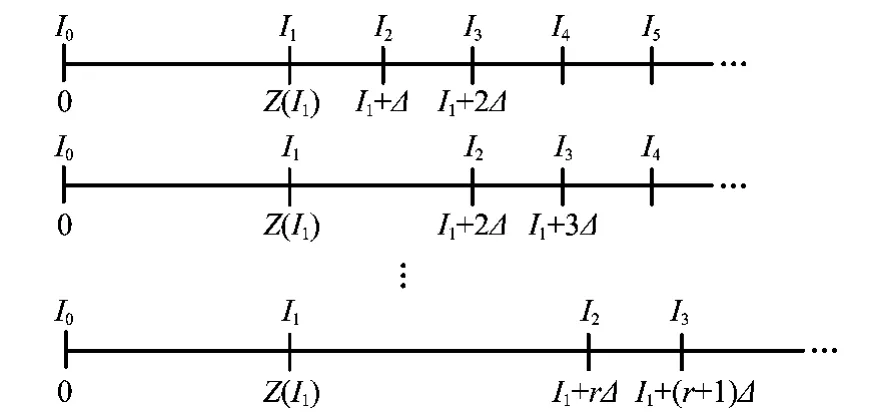
圖4 狀態(tài)檢測間隔期I2的可行解（τ＝I2；Z（I2））

隨著狀態(tài)檢測的進行，可依據(jù)上述求解步驟對狀態(tài)檢測間隔進行序貫決策，以使條件可用度最大化。需要指出的是，若在第n次檢測時得到Z（In）＝m，表明協(xié)變量狀態(tài)已經達到最差，不需要繼續(xù)進行狀態(tài)檢測，在kmΔ時刻執(zhí)行預防性更換即可。

在確定可行解執(zhí)行過程后，可確定條件可用度AP（u）的求解方法。令EA（u）表示條件期望可工作時間，TA（u）表示條件更換周期剩余時間長度，則

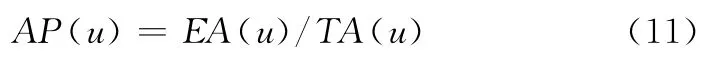
式中，u為下次檢測間隔期長度，由于檢測間隔期以Δ為單元，因此u應為Δ的整數(shù)倍。

本文假設裝備在初始時刻處于完好狀態(tài)，因此有I0＝0，Z（I0）＝1，因此在0時刻，EA（u）＝EA（u｜T＞I0，Z（I0））。依次類推，在第l次檢測完成時刻，EA（u）＝EA（u｜T＞Il，Z（I0）＝1，Z（I1）＝Z1，…，Z（Il）＝Zl），按照圖4所示的序貫檢測過程，EA（u）可通過遞歸運算進行求解

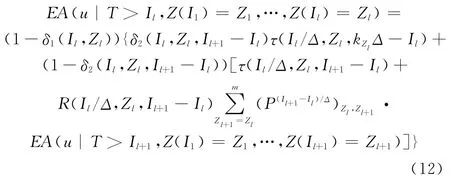
式中，δ1（Il，Zl）和δ2（Il，Zl，Il＋1－Il）為示性函數(shù)

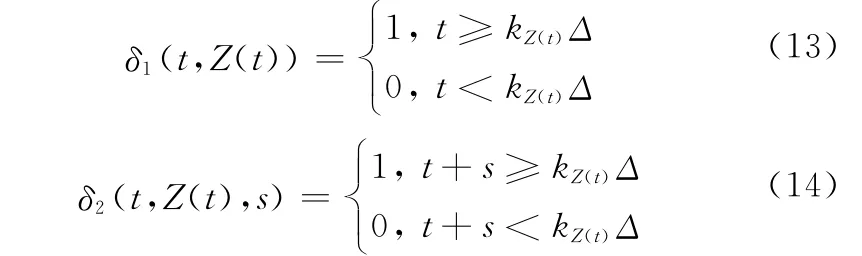
依據(jù)上述遞歸運算方法，構造Matlab迭代式

式中，j表示裝備已完成的單位檢測間隔數(shù)；i表示Z（jΔ）；u表示當期檢測間隔期；n表示當前已完成的檢測次數(shù)。

同樣，在0時刻TA（u）可表示為TA（u｜T＞I0，Z（I0）），依次類推，在完成第l次檢測時，TA（u）＝TA（u｜T＞Il，Z（I0）＝1，Z（I1）＝Z1，…，Z（Il）＝Zl），按照圖4所示的序貫檢測過程，該式可通過遞歸運算進行求解

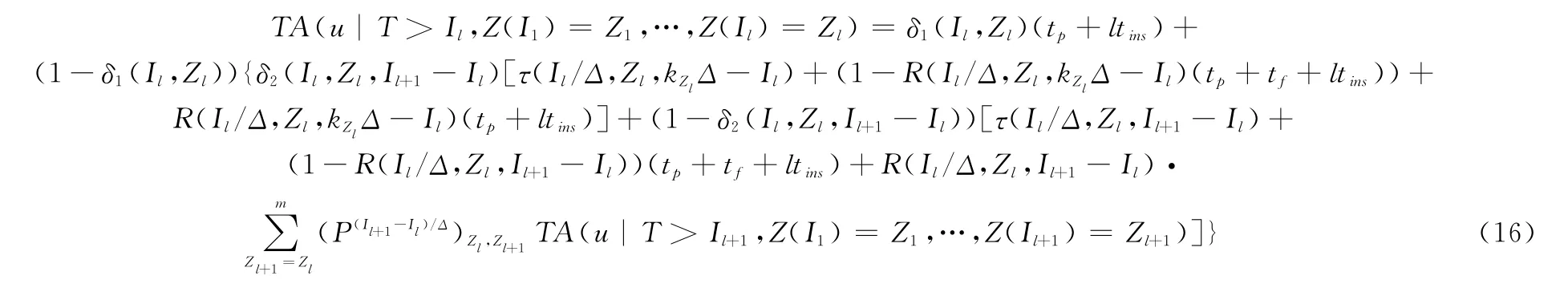
依據(jù)上述遞歸運算方法，構造Matlab迭代式

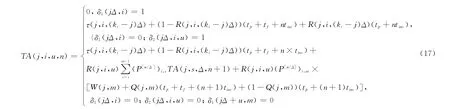
式中，tp為單次預防性更換的時間；tf為單次故障更換所需的額外時間；tins為單次檢測時間。在確定EA（u）和TA（u）的求解方法后即可對變步長檢測間隔進行優(yōu)化計算，步驟如下：

步驟1 由于狀態(tài)檢測間隔決策僅考慮未來的壽命區(qū)間，因此在可用度目標函數(shù)中不納入已完成檢測的成分，在每次決策時刻令當前檢測次數(shù)賦n＝0。

步驟2 已知當前時刻為jΔ，令τ＝j，將τ代入式（10）求得下一檢測間隔的可行解r。

步驟3 令u從1開始累加取值直到r，將當前時刻jΔ、當前協(xié)變量i、n＝0和u分別代入迭代式（15）和式（17），求得EA（u）和TA（u）；將EA（u）和TA（u）代入式（11），求得對應的AP（u），當AP（u）取得最小值時，對應的u即為當前檢測間隔期的最優(yōu)值。

在裝備初始部署階段，令j＝0，i＝1，n＝0，按照上述步驟求解EA（u）和TA（u），將計算結果代入式（11）計算AP（u），即可對首次檢測間隔進行優(yōu)化和決策。隨著狀態(tài)檢測的進行，可對狀態(tài)檢測間隔進行序貫的決策。

3 狀態(tài)維修決策實例分析

本文以某型裝備的發(fā)動機為維修對象，為該型發(fā)動機建立WPHM模型。利用文獻［16］采集到的油液顆粒濃度數(shù)據(jù)進行極大似然估計，得到的參數(shù)為：β＝7．294 6，η＝1 887，γ＝0．801 5。狀態(tài)檢測間隔Δ＝40h，裝備狀態(tài)空間由5個狀態(tài)組成，S＝｛1，2，3，4，5｝。假設預防性更換的時間tp為48h，tf＝9tp，則故障更換的時間為480h，單次檢測時間tins＝2h。為了簡化問題，假設狀態(tài)轉移概率為常數(shù)值，經極大似然估計得到的協(xié)變量狀態(tài)轉移概率矩陣為

利用式（3）～式（9）對可用度閾值進行求解，可以得到a＊＝0．921 0。各狀態(tài)對應的最優(yōu)預防性維修周期如表1所示。

表1 最優(yōu)預防性維修時間Δ

按照表1所示的最優(yōu)預防性維修時間，即可利用當前役齡及狀態(tài)觀測值進行維修行為決策。

首先對首次檢測時間I1進行決策，由表1可知，τ＝0，k1＝26，根據(jù)式（6）可求得r的取值范圍為｛1，2，…，26｝。利用式（11）～式（17）進行I1最優(yōu)化，結果如表2所示。

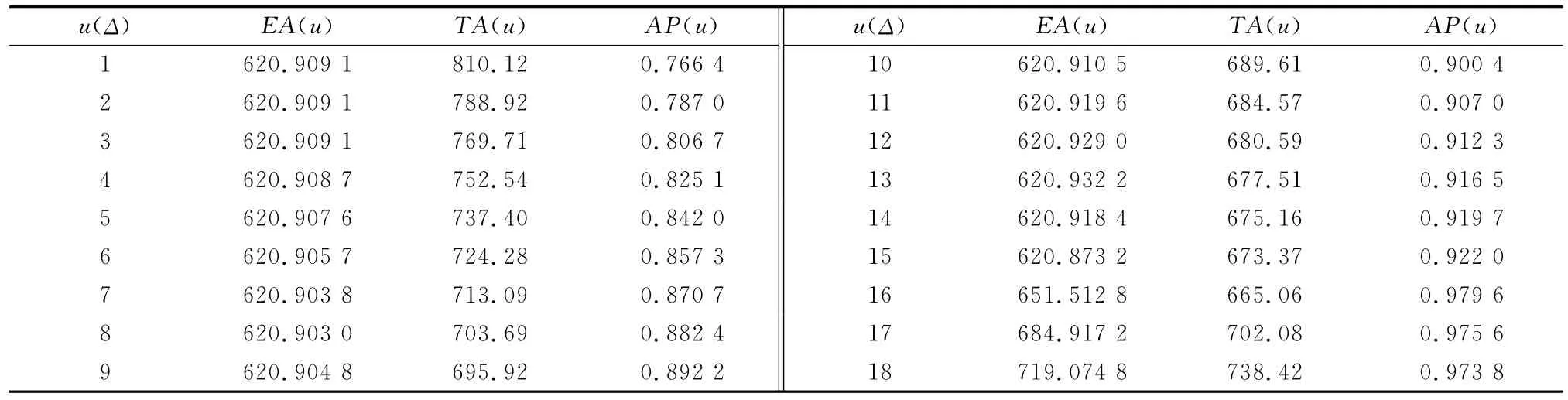
表2 不同u條件下I1的過程解（j＝0；i＝1）

由表2可知，當u＝16Δ時，裝備的期望可達可用度取得最大值0．979 6，因此首次檢測的最佳時間I1＝16Δ，即在裝備役齡達到640摩托小時后實施首次狀態(tài)檢測。

當裝備無故障運行到16Δ進行首次檢測時，Z（I1）可能為S中的任一狀態(tài)等級，此時應通過比較I1和kZ（I1）對是否進行預防性更換進行決策，若不進行預防性更換，則繼續(xù)運行并對I2進行決策。

如表3所示，I1＝16Δ，若觀測到Z（I1）為1，2，3或4時，有I1＜kZ（I1）Δ，裝備不需進行預防性更換，可對I2進行優(yōu)化決策，繼續(xù)使用；若觀測到Z（I1）＝5，由表中可知I1＝k5＝16，滿足預防更換條件，應立即實施更換。

若繼續(xù)進行狀態(tài)檢測，可得到與Z（I1）的觀測值一一對應的最佳下次檢測時間，如表3所示。隨著狀態(tài)檢測的序貫執(zhí)行，可進行相應的預防性更換和檢測間隔期決策。

按照上述決策過程，可以對狀態(tài)維修行為以及狀態(tài)檢測間隔期進行序貫的決策，從而達到使裝備的可用度最大化的目的。在其他條件相同的情況下，分別計算等間隔檢測及本文提出的動態(tài)檢測策略在初始時刻的期望可用度，等間隔檢測策略得到的期望可用度為0．916 6，本文提出的序貫檢測策略的期望可用度為0．979 6，顯著高于前者，因此本文提出的狀態(tài)維修決策方法能夠較好地提高裝備的可用度，為裝備遂行任務提供有力的支持。

表3 Z（I1）不同取值條件下I2的最優(yōu)值（I1＝16Δ）

4 結 論

狀態(tài)維修是提高裝備戰(zhàn)備完好性、降低壽命周期費用的有效維修方式，若單純依據(jù)狀態(tài)檢測信息進行維修決策，易影響狀態(tài)維修的應用效果。因此本文采用PHM模型將狀態(tài)檢測信息和役齡信息進行了有效的結合，更準確地描述了裝備狀態(tài)的劣化規(guī)律。

在完全檢測的條件下，本文以條件可用度為決策目標對狀態(tài)維修行為決策模型進行了研究，提出了相應的優(yōu)化算法。在確定維修行為決策閾值的基礎上，本文將故障更換、預防性更換以及狀態(tài)檢測等維修行為對裝備可用度的影響進行量化，構造了檢測間隔期的決策指標，并提出了檢測間隔期的序貫決策方法。案例分析表明，本文提出的狀態(tài)維修決策方法能夠通過減少不必要的狀態(tài)檢測降低其對裝備正常動用的不利影響，為提高裝備的戰(zhàn)備完好性提供有力的支持。

［1］Bengtsson M．Condition based maintenance system technologywhere is development heading［C］∥Proc．of the 17th European Maintenance Congress，2004：580－588．

［2］Zhao X L，Chen X F，Li B，et al．Review of life prediction for mechanical major equipment［J］．Journal of Mechanical Engineering，2011，47（11）：100－116．（張小麗，陳雪峰，李兵，等．機械重大裝備壽命預測綜述［J］．機械工程學報，2011，47（11）：100－116．）

［3］Castanier B，Berenguer C，Grall A．A sequential condition－based repair／replacement policy with non－periodic inspections for a system subject to continuous wear［J］．Applied Stochastic Models in Business and Industry，2003，19（4）：327－347．

［4］Amari S V，McLaughlin L．Optimal design of a condition－based maintenance model［C］∥Proc．of the Annual Reliability and Maintainability Symposium，2004：528－533．

［5］Wang W，Majid H B A．Reliability data analysis and modeling of offshore oil platform plant［J］．Journal of Quality in Maintenance Engineering，2000，6（4）：287－295．

［6］Ghasemi A，Yacout S，Ouali M S．Optimal condition based maintenance with imperfect information and the proportional hazard model［J］．International Journal of Production Research，2007，45（4）：989－1012．

［7］Wang W．Modeling condition monitoring intervals：a hybrid of simulation and analytical approaches［J］．Journal of the Operational Research Society，2003，54（3）：273－282．

［8］Han D，Li S L．Research on preventive maintenance period of electronic equipment based on availability［J］．Journal of Ordnance Engineering College，2008，20（5）：12－15．（韓東，李石磊．基于可用度的電子裝備預防維修周期研究［J］．軍械工程學院學報，2008，20（5）：12－15．）

［9］Ansell J，Phillips M．Practical aspects of modelling of repairable systems data using proportional hazards models［J］．Reliability Engineering and System Safety，1997，58（2）：167－171．

［10］Jiang S T，Landers T L，Rhoads T R．Assessment of repairable－system reliability using proportional intensity models：a review［J］．IEEE Trans．on Reliability，2006，55（2）：328－336．

［11］Jardine K S，Anderson P M，Mann D S．Applications of the Weibull proportional hazards model to aircraft and marine engine failure data［J］．Quality ＆Reliability Engineering International，1987，3（2）：77－82．

［12］Lawless J F．Statistical model and methods of life data［M］．Beijing：China Statistical Press，1998．

［13］Ghasemi A，Hodkiewicz M R．Estimating mean residual life for a case study of rail wagon bearings［J］．IEEE Trans．on Reliability，2012，61（3）：719－730．

［14］Markis V，Jardine A K S．Optimal replacement in the proportional hazard model［J］．Information Systems and Operational Research，1992，20（1）：172－183．

［15］Ghasemi A．Condition based maintenance using the proportional hazard model with imperfect information［D］．Ottawa：University of Montreal，2005．

［16］Chen L．Research on condition based maintenance model and its application［D］．Shijiazhuang：Ordnance Engineering College，2009．（陳麗．基于狀態(tài)的維修模型及應用研究［D］．石家莊：軍械工程學院，2009．）

E－mail：aafe77330＠163．com

張耀輝（1960－），男，教授，博士，主要研究方向為裝備維修理論與技術。

E－mail：zyh532＠sohu．com

韓小孩（1987－），男，博士研究生，主要研究方向為裝備維修理論與技術。

E－mail：hanleiacd＠163．com

Task oriented condition－based maintenance decision－making of equipment

WANG Shao－h(huán)ua，ZHANG Yao－h(huán)ui，HAN Xiao－h(huán)ai
（Department of Technology Support Engineering，Academy of Armored Force Engineering，Beijing 100072，China）

Aiming at the disadvantage of periodic maintenance，a condition description model of equipment based on Weibull proportional hazards model（WPHM）is proposed and taken as the foundation for conditionbased maintenance（CBM）decision－making．In terms of the most emphasized tasks properties in equipment，CBM actions and condition inspection intervals are studied as the major contents which take the availability as decision－making objective function．The deteriorate process of covariate condition is presented in the form of transition matrix，and the maximized conditional availability is taken as the optimization target to determine the detailed decision－making methods and related algorithm．Finally，a case study is illustrated to verify the feasibility and reasonability of the method．

condition－based maintenance decision－making；proportional hazards model（PHM）；covariate parameter；inspection interval

E 92

A

10．3969／j．issn．1001－506X．2015．06．16

王少華（1986－），男，博士研究生，主要研究方向為裝備維修理論與技術。

1001－506X（2015）06－1325－06

2014－06－05；

2014－08－02；網絡優(yōu)先出版日期：2014－10－30。

網絡優(yōu)先出版地址：http：／／www．cnki．net／kcms／detail／11．2422．TN．20141030．1139．017．html

軍隊科研計劃項目（51327020303）資助課題