基于LS-DYNA的深溝球軸承動態仿真分析

劉江山，宋麗，陸超

(上海市軸承技術研究所，上海 201801)

球軸承是精密的機械零件，轉動過程中各零件之間的力學關系復雜，對滾動軸承進行動力學分析和數值模擬研究已成為趨勢[1]。隨著計算機技術的發展，運用CAE技術對球軸承進行動態仿真，已經成為球軸承產品設計、制造、分析以及檢測等領域不可缺少的工具，具有一定的工程意義。

1 動態特性仿真分析的基本理論

1.1 LS-DYNA動態仿真軟件

文獻[2]首先應用Hertz理論建立了球軸承的靜力學分析模型，并推導出了鋼球的最大承受載荷Qmax與徑向載荷Fr的關系式。文獻[3]中DYNA程序采用顯式的中心差分格式，用于分析爆炸與高速沖擊等過程中的大變形動態響應問題，該程序經過不斷規范和完善，使得LS-DYNA程序系列的應用范圍不斷擴大，并建立起完善的軟件質量保證體系，使其得到廣泛使用，LS-DYNA程序的分析流程如圖1所示。

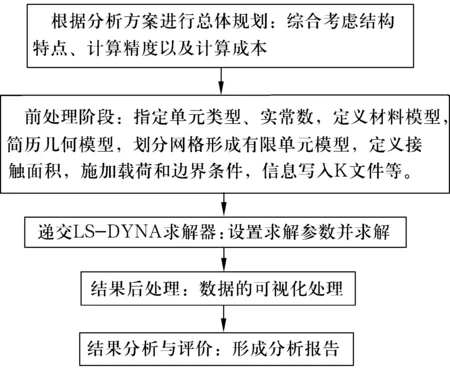
圖1 LS-DYNA分析流程圖

1.2 LS-DYNA動態仿真基本理論

在求解滾動軸承動態特性仿真分析中，一般采用中心差分法，該方法不需要進行平衡迭代，也不需要直接求解切線剛度，因此求解速度快，節省計算時間[4]。

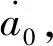
(1)

將位移at+Δt在t時刻進行Taylor展開，取最高的二次多項式，其近似值為

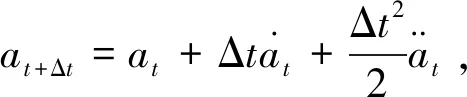
(2)

將(2)式進行求解后得到加速度與位移的關系為

(3)

速度與位移的關系為

(4)

將(3)式和(4)式代入(1)式可得中心差分法的經典公式為

(5)

由(5)式可知，若已知at-Δt和at，則可解出at+Δt，進而求出t時刻的速度和加速度。

2 有限元模型的建立

2.1 實體模型的建立

深溝球軸承是一種較具有代表性的滾動軸承，選擇型號為608-2RS的深溝球軸承進行仿真分析，研究其轉動過程中應力、應變場的變化以及振動情況，結構參數見表1。

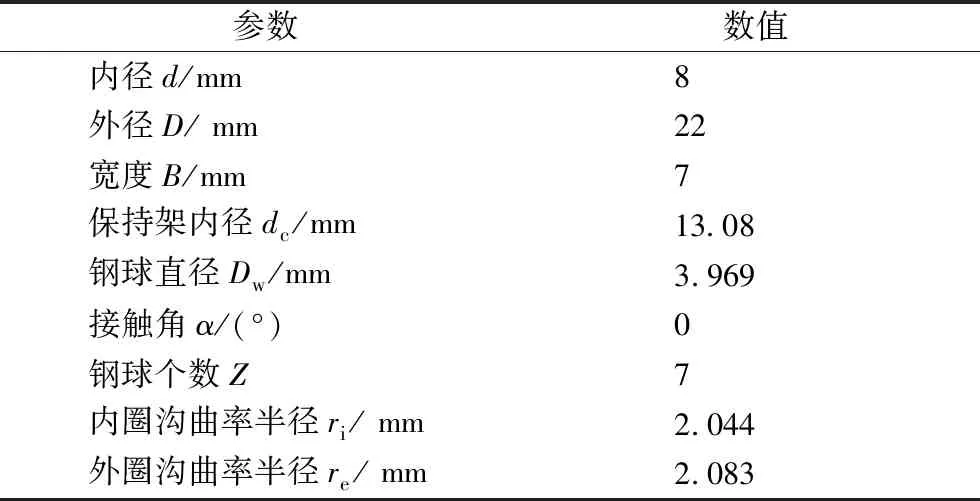
表1 608-2RS球軸承結構參數表

根據表中參數，在UG中建立球軸承三維實體模型，考慮到軸承實際模型的復雜性和現有計算機仿真的局限性，且軸承倒角、油膜等因素對整體動態特性影響很小，因此忽略軸承倒角、游隙以及密封防塵和潤滑的影響。得到608-2RS深溝球軸承的三維實體模型如圖2所示。

圖2 608-2RS深溝球軸承三維模型圖

2.2 有限元模型的建立

軸承實體模型導入LS-DYNA后，先定義顯式單元Solid164和Shell163及其算法。定義內圈、外圈和鋼球材料為GCr15，其彈性模量為208 GPa，泊松比為0.3；定義保持架材料為08F碳素鋼，其彈性模量為219 GPa，泊松比為0.3。對內、外圈進行掃略劃分網格，鋼球進行映射劃分網格，保持架進行自由網格劃分，且鋼球與保持架接觸部位進行局部網格細化，有限元模型如圖3所示。

圖3 608-2RS球軸承有限元模型

3 動態仿真及結果分析

假設軸承工作時承受的徑向載荷Fr為500 N，軸承轉速為1 800 r/min，為了模擬軸承實際承載過程，載荷施加在內圈下半部的剛性面上，轉速施加在內圈剛性面上；在外圈外表面上間隔45°選取4個位置，分別對該位置上的節點施加x和y方向的移動約束以及x，y，z方向的轉動約束，加載和約束后的有限元模型如圖4所示。

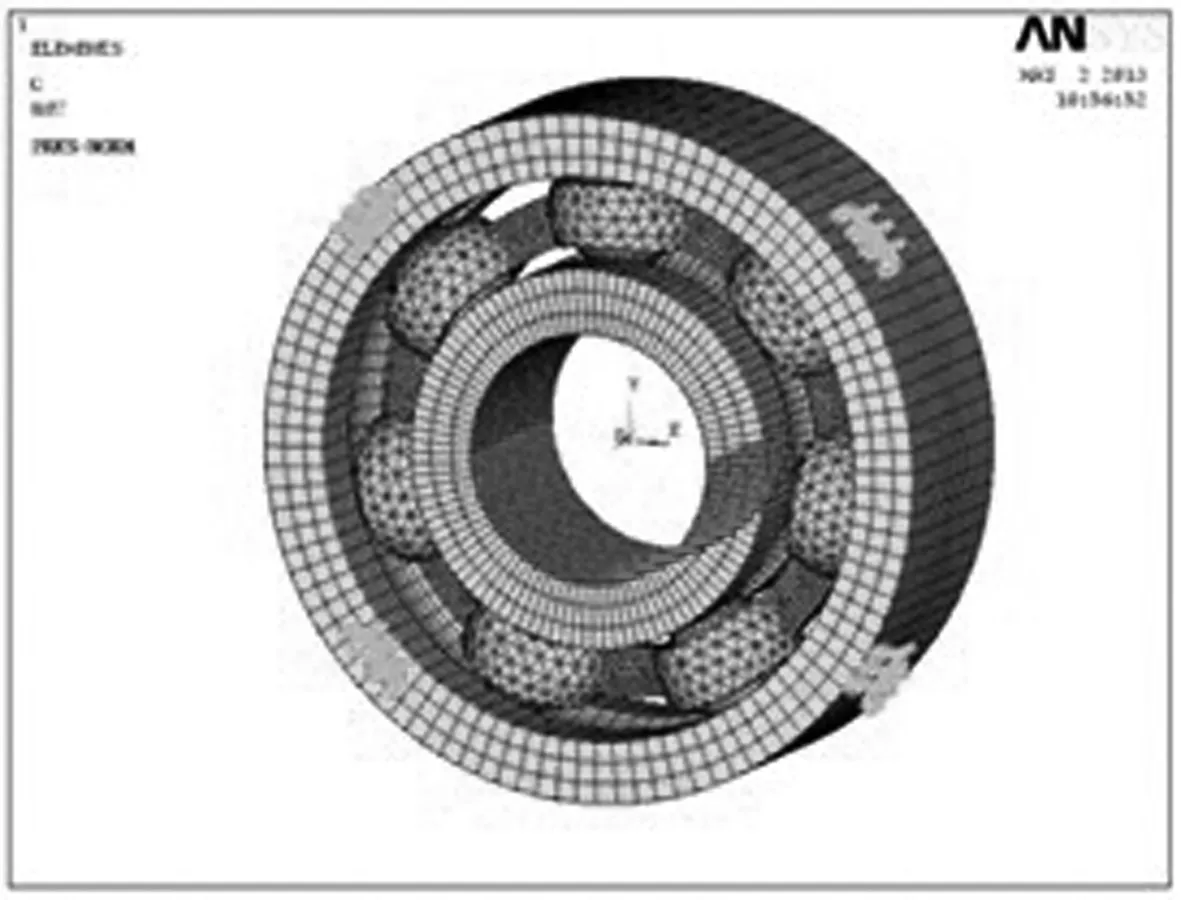
圖4 加載和約束后的608-2RS軸承有限元模型圖

3.1 等效應力分析

分別取4個時刻分析內圈速度和軸承應力，結果如圖5所示。

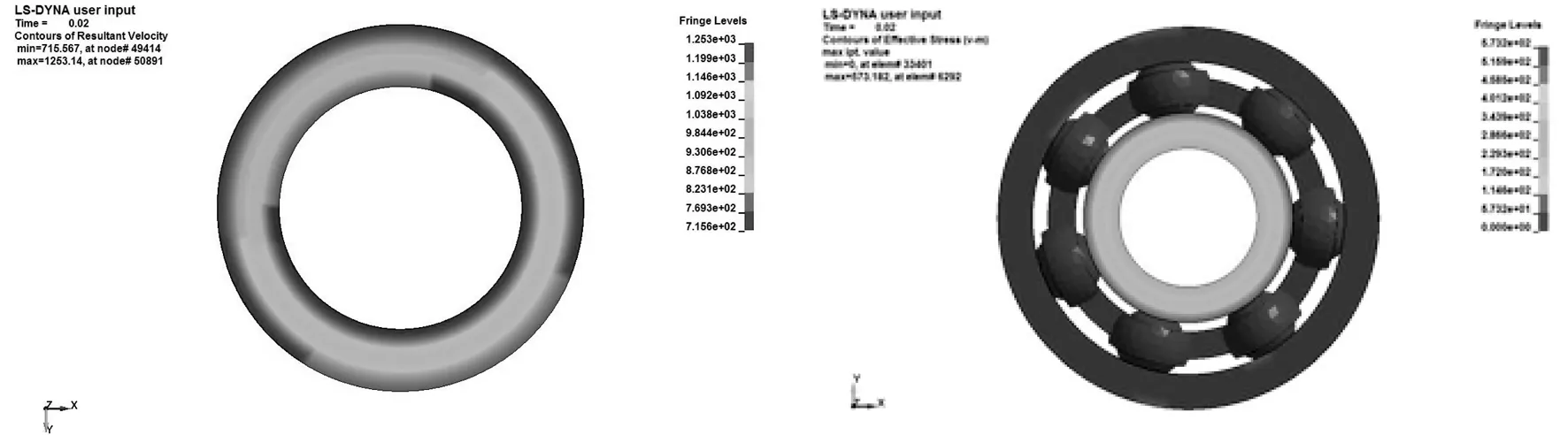
(a)0.02 s

(b)0.05 s

(c)0.08 s

(d)0.1 s

由圖5可知，在0.02 s時軸承承受的最大等效應力出現在內圈和軸的接觸區域，其值為573.182 MPa；0.05 s時軸承承受的最大等效應力出現在鋼球和內圈的接觸區域，其值為496.063 MPa；0.08 s時軸承承受的最大等效應力出現在鋼球和內圈的接觸區域，其值為400.012 MPa；0.1 s時軸承承受的最大等效應力出現在鋼球和外圈的接觸區域，其值為324.243 MPa。鋼球與內、外圈接觸區域的應力較大，且最大應力值和其位置都會隨著軸承的運轉而發生變化。

3.2 切片應力云圖分析

為了全面分析仿真過程中軸承內部的應力分布情況，對整個軸承進行切片處理，0.05 s時其應力云圖如圖6所示。

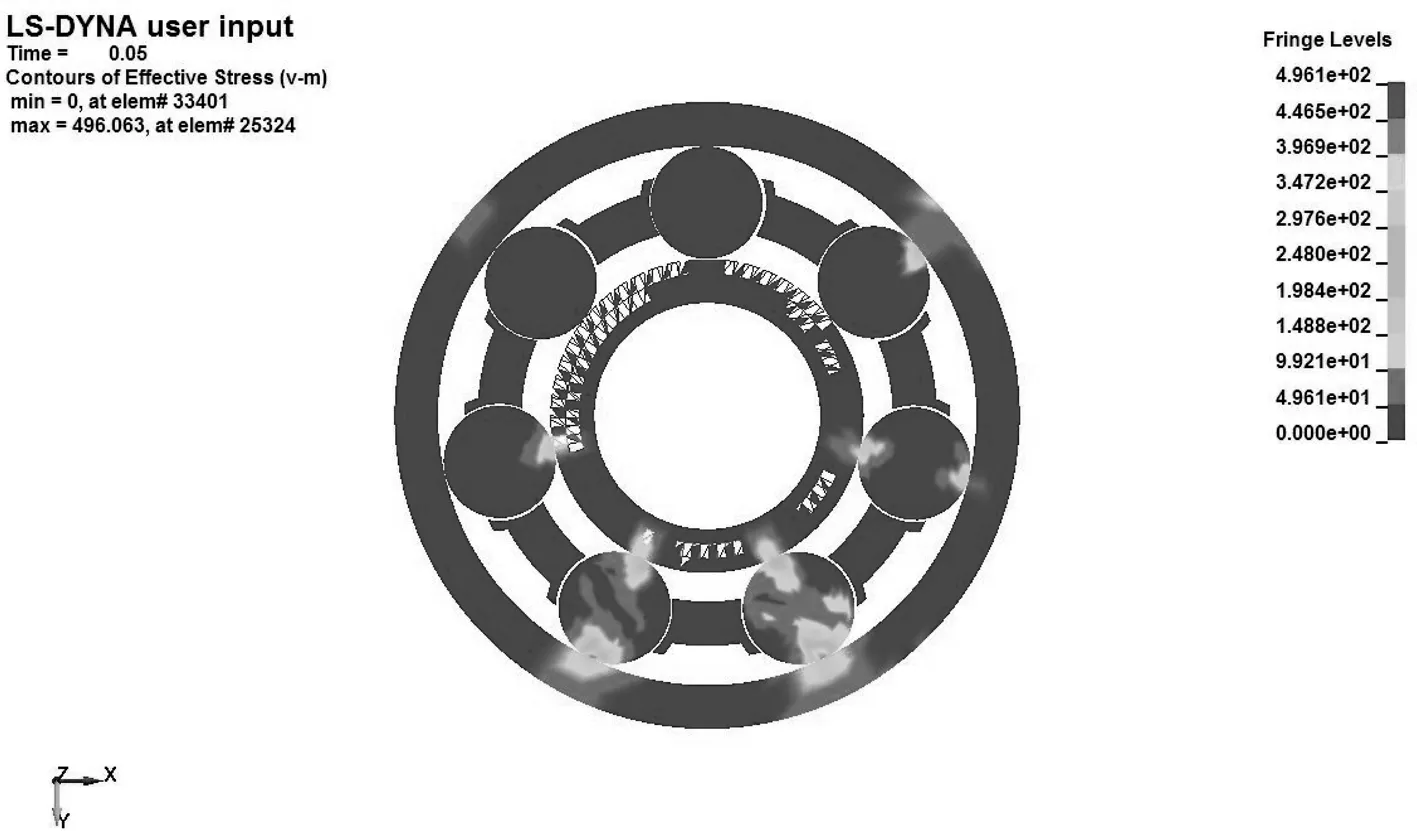
圖6 0.05 s時軸承切片應力云圖

由圖6可知，最大應力出現在鋼球和內、外圈接觸表面以下的某一區域，并且其值由內向外逐漸減小，應力主要分布在軸承的承載區，承載區的應力明顯大于非承載區，且應力分布區域呈橢圓形。

3.3 運動學分析

拾取鋼球表面上的單元節點，繪制其沿x方向的速度時程曲線，結果如圖7所示。

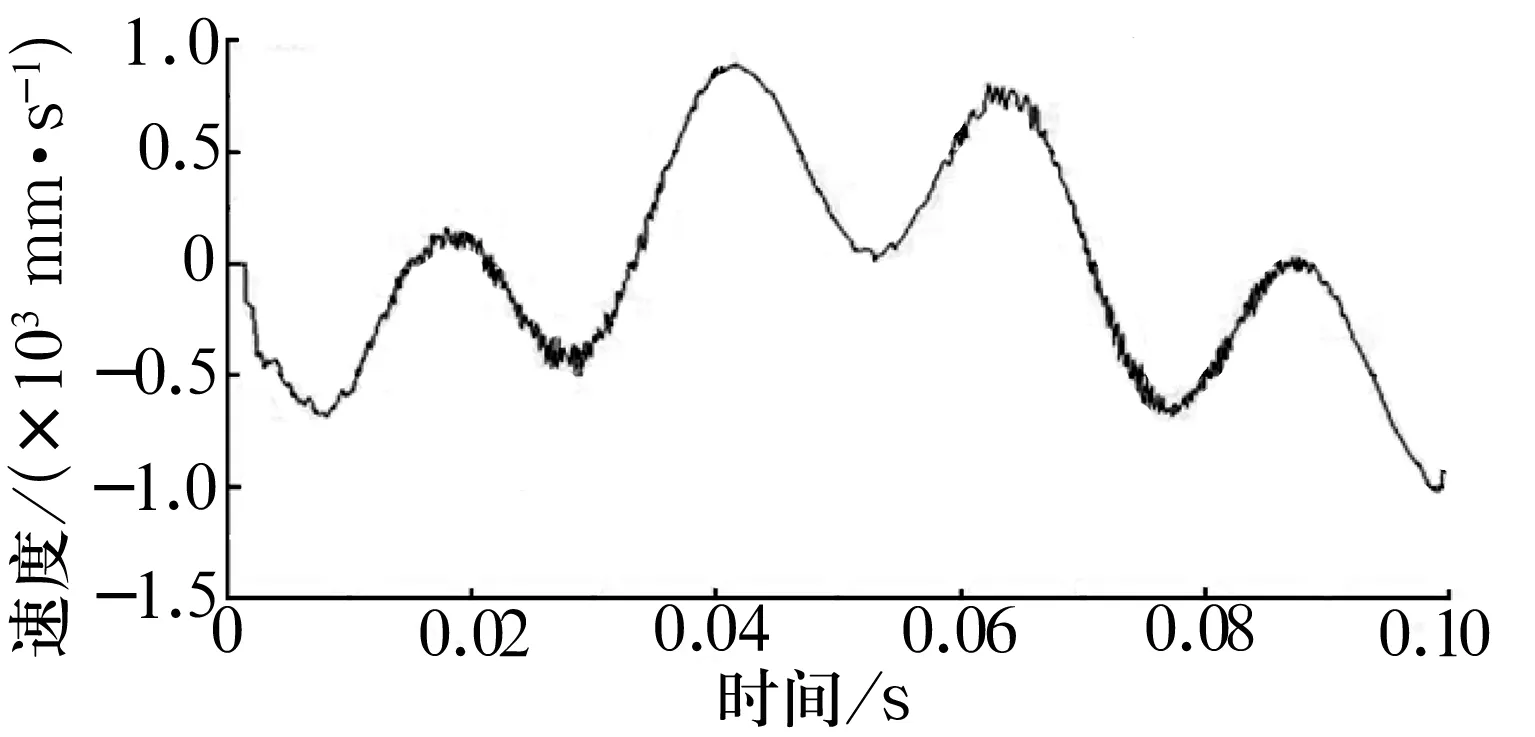
(a)沿x向的速度時程曲線

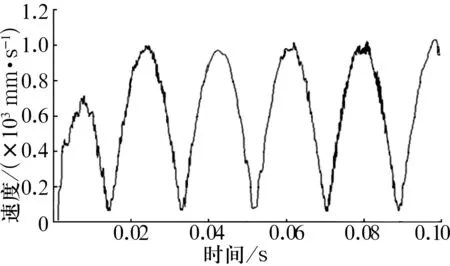
(b)綜合速度時程曲線

由圖7可以看出，鋼球表面單元節點的速度曲線呈明顯的周期性，周期約為0.037 5 s，單元節點在某些時刻附近x向的速度值為0，由于軸承在工作過程中內圈轉動、外圈靜止，此時鋼球單元節點與內溝道接觸時刻速度達到相應的最大值或最小值，與外溝道接觸時刻速度為0，故此時鋼球單元節點與外圈接觸；該單元節點在0.043 s附近x方向的速度達到正的最大值為0.894 m/s，此時單元8節點與內圈下表面接觸；單元節點在0.097 s附近x方向的速度達到負的最大值為-1.019 m/s，此時單元節點與內圈上表面接觸。

根據上述分析，將提取的有限元結果與理論計算出的鋼球自轉角速度和質心線速度進行比較，結果見表2。

表2 線速度和自轉角速度的理論值與仿真值

由表2可以看出，有限元解和數值解誤差較小，表明采用ANSYS/LS-DYNA有限元法分析軸承的動態特征這一方法是可行的。

3.4 振動情況分析

為了反映軸承在轉動過程中的振動情況，選取鋼球接觸區域的單元節點進行分析，其加速度的時程曲線如圖8所示。

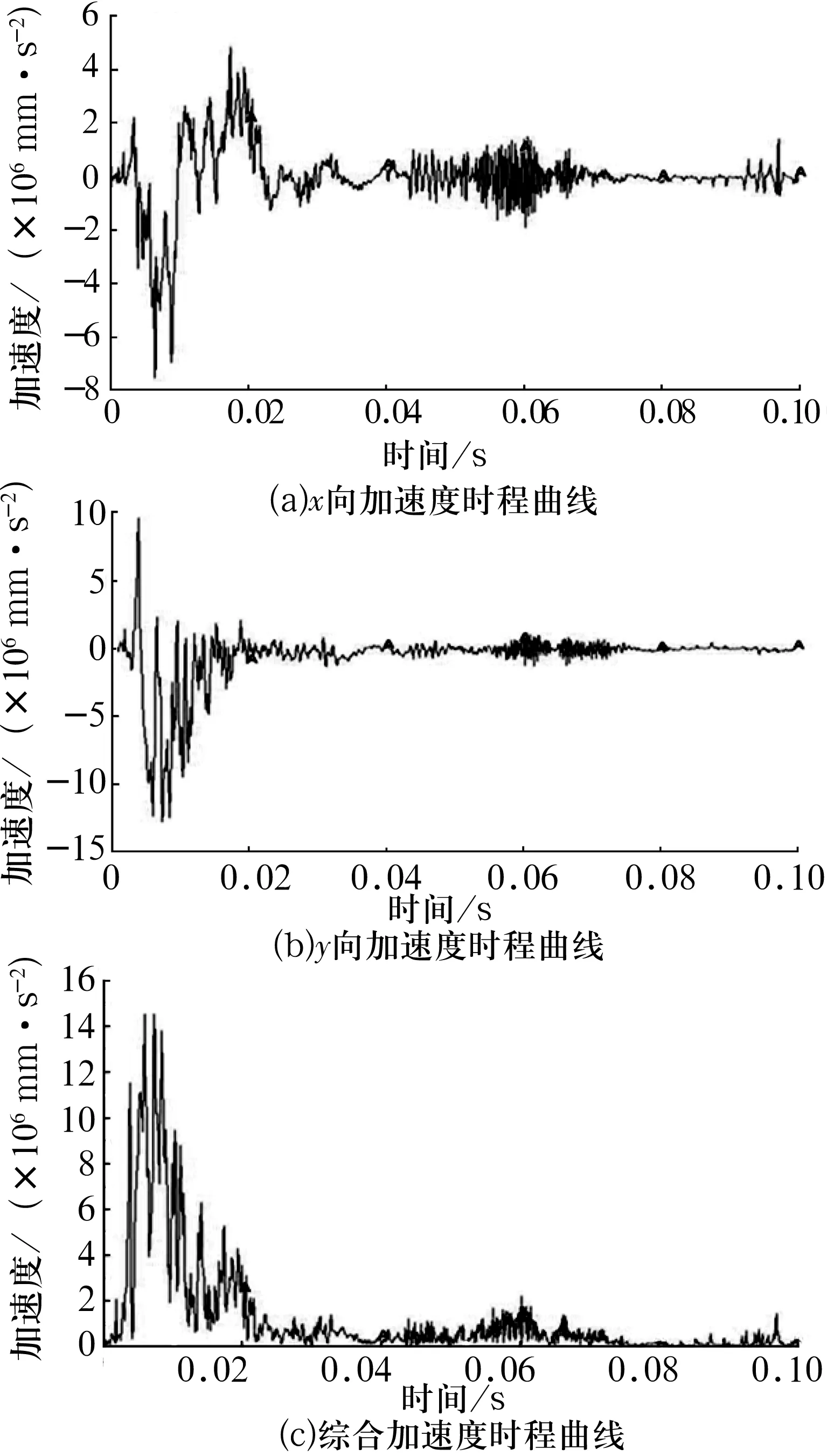
圖8 接觸區域鋼球單元點加速度時程曲線

由圖8可知，接觸區域鋼球上單元點在0～0.02 s加速度值波動較大，在軸承啟動時，由于鋼球受突加載荷的作用而產生強烈振動，而后又趨于緩和，但在0.06 s時鋼球因受到突加轉速的作用而使加速度值有小幅度的增加，軸承處于正常運轉狀態時，此節點處的加速度減小到約為零且趨于平穩變化狀態。鋼球加速度時程曲線沒有明顯的周期性，這種無規則的振動也說明軸承運轉時產生較強的非線性特性，產生這種現象的原因是軸承在工作過程中產生非線性接觸變形以及軸承元件運轉時自由度的復雜性，同時由仿真可知，軸承的振動加速度隨軸承轉速的增大而增大。

3.5 實例應力計算對比

鋼球承受的最大徑向載荷為

(6)

將球軸承參數代入(6)式可得Qmax為357.14 N。

外圈、內圈以及鋼球的曲率(凸面曲率值為正，凹面曲率值為負；下標xy，yz分別為軸向平面和徑向平面)分別為

(7)

(8)

(9)

主曲率為

∑ρ=2ρw+ρxy+ρyz。

(10)

鋼球與套圈接觸橢圓的長、短半軸分別為

(11)

鋼球與外圈接觸時，代入相關參數可得主曲率∑ρ=0.417 9；利用插值法查詢Hertz接觸系數表可得接觸橢圓系數ea=0.09，eb=0.01，εE=1。代入(11)式可得a=0.854 mm，b=0.095 mm。故最大接觸應力Pemax= 3Qmax/2πab=986.8 MPa，平均接觸應力Pem=Qmax/πab=657.87 MPa。

同理，鋼球與內圈接觸時，主曲率∑ρ=0.699 9，ea=0.106 6，eb=0.008 93,εE=1，a=0.852 mm，b=0.071 mm。最大接觸應力Pimax=935.55 MPa，平均接觸應力Pim=623.7 MPa。

鋼球與內、外圈接觸時應力的理論計算結果和有限元仿真結果見表3。由表可知，軸承應力的理論計算結果與仿真結果比較接近，驗證了仿真的可行性。

表3 應力計算和仿真結果對比 MPa

4 結束語

文中以608-2RS型深溝球軸承為研究對象，首先運用建模軟件UG建立了三維簡化模型，再將其導入仿真軟件LS-DYNA進行有限元分析，研究了深溝球軸承在運轉過程中的接觸應力、轉速和振動的變化規律，通過與理論值的對比證明了仿真的可行性。