妙用質點組動量定理速解題

華峰

質點組動量定理的內容是：在一段時間內質點組動量的增量，等于作用于質點組外力矢量和在這段時間內的沖量.因此，內力（質點間的相互作用力）只影響質點動量的變化，不影響質點組動量的變化.在求解有關動量問題時，我們常會遇到由兩個質點組成的質點組，在恒定外力作用下，質點間有相互作用和相對運動的簡單情形.在這種情況下，質點組的動量定理用Ft =Δp來表示，其中F為恒定外力，t為恒定外力作用時間，Δp為質點組（也可稱系統）總動量的變化.求解此類問題時，利用上式確定系統總動量的變化、恒定外力及作用時間之間的關系，結合牛頓運動定律以及運動學公式，可使問題化難為易，較其他方法更為簡單、快捷.

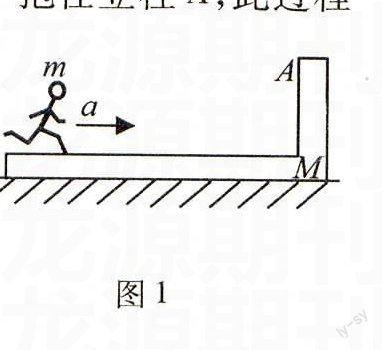
例1如圖1所示，一長木板右端固定一立柱A，總質量為M，一質量為m的人從木板左端開始，以恒定的加速度向右奔走，木板相對地面向左滑動，人

跑到右端迅速（所用時間極短）抱住立柱A，此過程所用時間為t，圖1此后再經過時間t′，人與木板停止運動.則（ ）.

A. t′B. t′>t

C. t′=t

D. 不能確定

解析設向右的方向為正方向（下同），木板與地面間的動摩擦因數為μ，人抱住立柱前，人與木板構成的系統總動量為p，人抱住立柱系統總動量為p′.因為人抱住立柱所用時間極短，系統動量幾乎不變，所以有p′=p.

整個過程中人與木板間的相互作用力是內力，對系統總動量變化沒有影響，系統總動量的變化是地對木板的摩擦力作用的結果.則由質點組動量定理：

對人抱住立柱前的過程有：

μ（M + m）gt=p

對抱住立柱后（摩擦力反向）的過程有：

-μ（M+m）gt′=0-p′

聯立以上三式可解得：t′=t.故應選C.

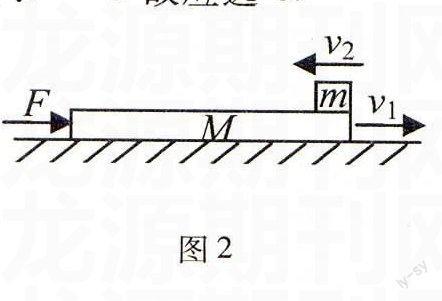
例2如圖2所示，在光滑水平面上，質量為M的木板正以速度v1向右運動.現有一質量為m的物塊以初速度v2向左運動，M與m間動摩擦因數為μ，木板足夠長.要使M始終勻速運動，需及時給木板施加一個水平力F，當物塊與木板的速度相等時，將力F去掉，求此過程中水平力F所做的功.

解析當物塊在木板上滑動時，木板在水平方向受力平衡，所以有；F=μmg.

因為物塊和木板組成的系統的總動量的變化是由F的作用引起的，則由質點組動量定理有：Ft=（M+m）v1- （Mv1-mv2）

在時間t內M的位移為：s=v1t

在這段時間內力F做的功為：W=Fs

聯立以上四式可解得：W=mv1（v1+v2）.

點評利用質點組動量定理求解，有效地避免了詳細分析物塊m運動具體過程所帶來的麻煩，極大地簡化了解題過程.

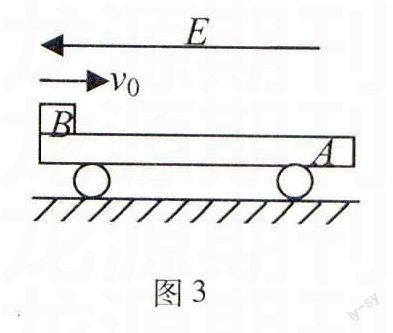
例3如圖3所示為一模擬貨物傳送的裝置，A是一個表面絕緣、質量M=100 kg、電量q=+6.0×10 C的傳送小車，小車置于光滑的水平地面上.在傳送途中有一水平電場，電場的強度E =4.0×103 V/m，可以通過開關控制其有無.現將質量m=20 kg的貨物B放置在小車左端，讓它們以v0=2 m/s的共同速度向右滑行，在貨物與小車快到終點時，閉合開關產生一個水平向左的勻強電場，經過一段時間后關閉電場.當貨物到達目的地時，小車和貨物的速度恰好為零.已知貨物與小車間的動摩擦因數為μ=0.1，為了使貨物不滑離小車的另一端，小車的最小長度L應為多少？（貨物不帶電且體積大小不計，g=10 m/s2）

解析傳送貨物的全過程分為兩個階段：第一階段有電場力作用，是電場力的作用使A和B構成的系統的總動量發生改變，第二階段為關閉電場后，A與B間有相互作用和相對運動直至速度均變為零，此階段A與B構成的系統總動量守恒且為零，整個系統動量變為零是電場力作用的結果，則由質點組動量定理有：

-qEt=0-（M+m）v0，代入已知數據可解得：t=1 s.

對于A：有電場時，在水平方向受電場力和摩擦力作用，其加速度為aA1（向左），先向右減速至速度為零，又向左做勻減速運動，且加速度不變；關閉電場后，A在B的摩擦作用下，加速度為aA2（向右），向左做勻減速運動直至速度為零.則aA1=

-qE+μmgM=-2.2 m/s2，aA2=μmgM=-0.2 m/s2.

對于B：有無電場，B均只受摩擦力作用，加速度為aB，方向向左，一直做向右的勻減速運動，直至速度為零.則aB=-μmgm=-μg=-1 m/s2.

關閉電場時，小車速度v車=v0+aA1t=-0.2 m/s.

全過程小車位移s車=v2車-v202aA1+0-v2車2aA2=

0.8 m，貨物位移s物=-v202aB= 2 m.

故小車長度至少為L=s物-s車=1.2 m.

點評在運用質點組動量定理求出電場力作用時間t的基礎上進行一系列順理成章的運算，避免了應用動量守恒、能量關系以及解方程組，不僅簡化了解題過程，而且簡捷、明了，從而順利、快速獲解.

（收稿日期：2015-02-08）