四旋翼姿態解算算法的對比與研究
王曉初,盧 琛
(廣東工業大學 機電工程學院,廣州 510006)
0 引言
在捷聯式慣性導航中,飛行器的姿態是機體坐標系相對于導航坐標系決定的,而描述這種坐標系的關系可以分為三類,有三參數法、四參數法和九參數法。其中三參數法也叫歐拉角法,四參數法有四元數,九參數法為方向余弦[4]。
利用慣性元件,對飛行器的姿態的解算,是捷聯式慣性導航的關鍵。文獻[6]從信號的頻域出發,給出了基于互補濾波器的解算算法。文獻[2]結合卡爾曼濾波器,給出了基于狀態空間的最優解算法。文獻[7]采用梯度下降為修正準則,給出了偏差沿梯度負方向修正算法。文獻[5]則結合梯度下降與互補濾波器,吸收了各自的優點。本文針對這幾種常見的姿態解算算法,從設計準則與實際應用出發,對比分析了各自算法的特點與相似之處。
1 姿態的更新算法
姿態的更新常采用如下流程,將角速度向量[ω]帶入四元數微分方程并求解,即可更新四元數[q]。
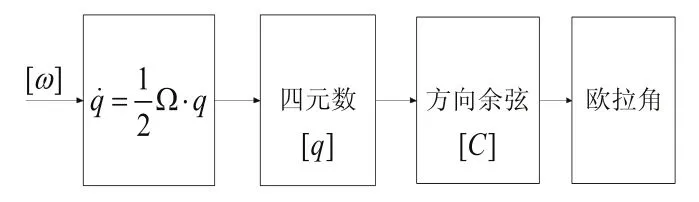
圖1 姿態解算流程
四元數微分方程為:

其中,四元數q定義為:q=q0+q1i+q2j+q3k。
寫成矩陣形式為:
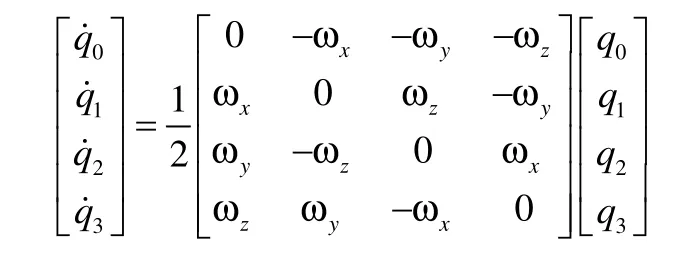
用角增量算法求解微分方程迭代格式為:

其中:
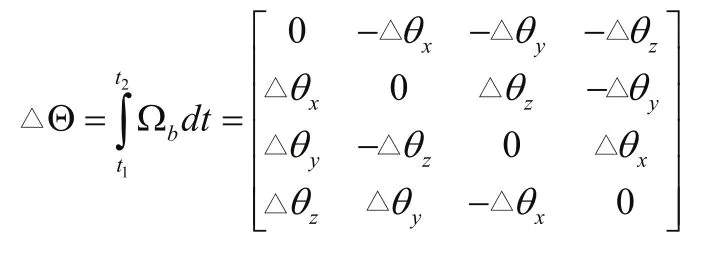
將cos和sin泰勒展開,取一階近似有:
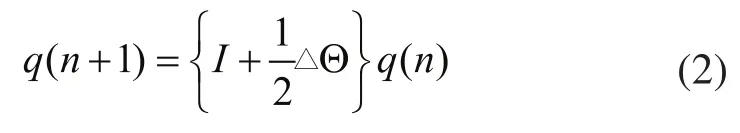
采用式(2)即可更新四元數,但是直接使用四元數不利于PID控制,還需利用方向余弦矩陣[C]將四元數轉變為歐拉角。
方向余弦矩陣也稱作坐標變換矩陣,是導航坐標系[Xn]到運載體坐標系[Xb]的變換矩陣,有并且方向余弦有兩種表示方法,分別為為四元數表出和歐拉角表出,并且兩種表出矩陣在同一坐標系下是等價的[1]。
四元數表示方向余弦為[1]:
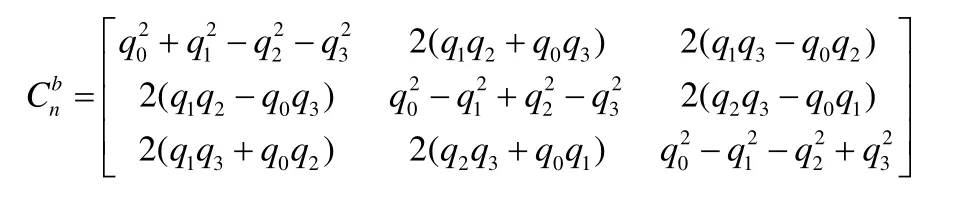
另外,歐拉角表出方向余弦為[1]:
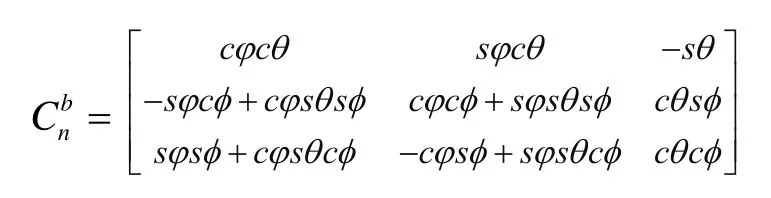
其中c和s分別代表cos和sin,?、θ和φ分別代表歐拉角中的航向角,俯仰角和橫滾角[1]。如果已知方向余弦,可以由下列公式求得對應的歐拉角:
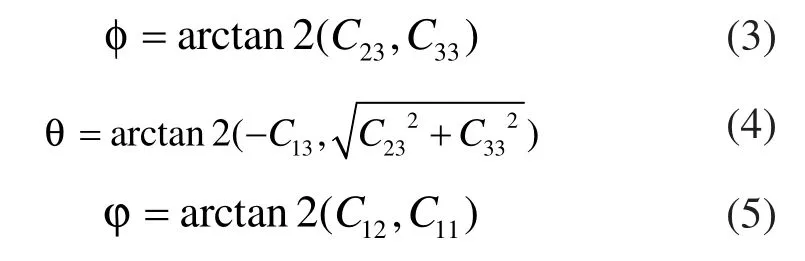
如圖1所示,式(2)給出了四元數法的更新迭代格式,更新四元數后即可求得方向余弦,由式(3)~式(5)便可求得到更新之后的歐拉角。
但是整個過程是建立在對角速度的積分,由于字長丟失精度會導致積分誤差,且誤差會隨著時間的延長而加大。所以需要組合加速度傳感器來修正姿態矩陣,使誤差項逐步減小,最終消除。常用的組合算法有互補濾波算法、梯度下降算法和卡爾曼濾波算法等。
2 常見組合算法的特點
姿態解算算法可以用圖2表示,其中由式(2)更新的姿態為qg,它是整個姿態估計q的基礎。

圖2 姿態解算算法流程
因為積分誤差的存在,所以需結合加速度計的輸出qc構成修正偏差ε(q),然后以不同的設計準則構成算法修正qg,即可得到在特定評判標準下的最優估計姿態q。
2.1 以高通和低通濾波器為修正算法
陀螺儀動態響應特性好,但會產生積分誤差。加速度傳感器測量姿態沒有積分誤差,但是動態響應較差。它們在頻域上的特性形成互補,從而提高測量精度和系統的動態性能[3]。
如圖3所示[6],表示互補濾波器的輸出姿態矩陣,代表載體坐標下的測量加速度單位向量,代表在慣性坐標系下的重力場向量,設。
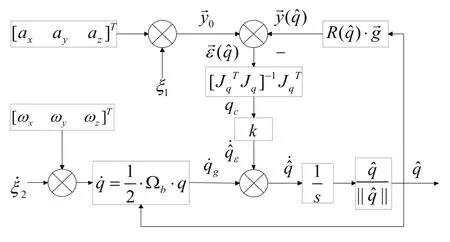
圖3 互補濾波器模型
其中誤差向量定義為:

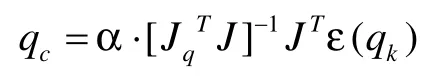
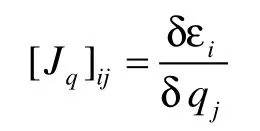
則整個互補濾波器的估計輸出為:
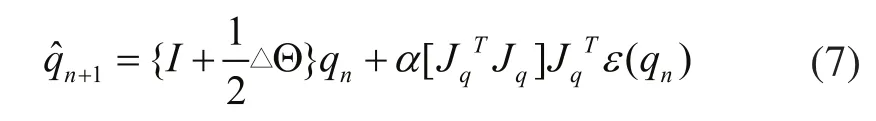
如圖3所示,令ξ1為加速度計測量噪聲,為陀螺儀測量噪聲,則噪聲傳遞函數為:
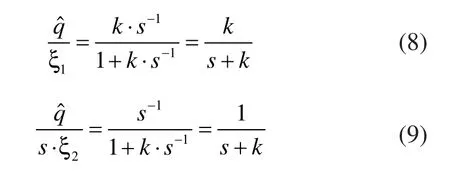
式(8)和式(9)可以用來設計k的取值,從而確定互補濾波器的截止頻率在大于fτ的高頻段,陀螺儀對解算起主要作用,反之,加速度對解算起主要作用[3]。
2.2 以偏差函數梯度負方向為修正準則
使用式(6)為目標函數,則有梯度:
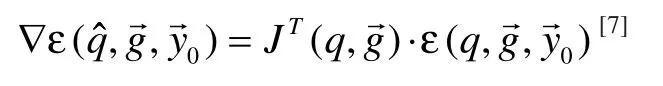
這樣就可以通過下列公式進行修正:
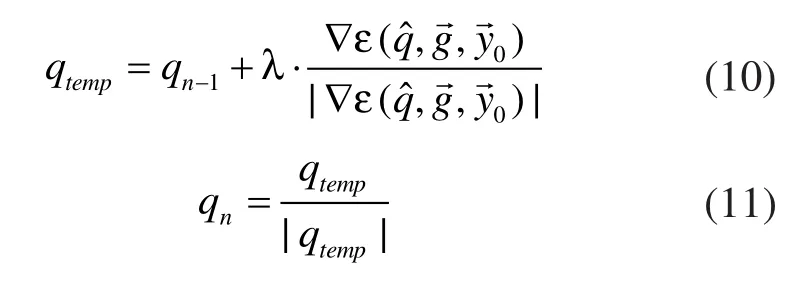
式(10)、式(11)即為梯度下降迭代格式,其中步長λ用來限制偏差收斂速度,但過大的步長可能會導致估計不準確[5]。
2.3 以卡爾曼濾波器為基礎的修正算法
卡爾曼濾波器以狀態空間為基礎,把信號過程看做在白噪聲作用下的線性輸出[5],
算法表述為:最優值=預測值+kg.修正量,其中kg為動態調整增益。
考慮如下線性系統離散模型:
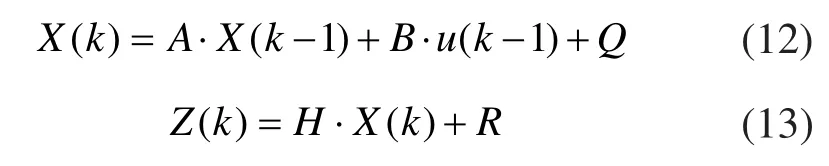
其中X(k)是系統的狀態向量,A是狀態轉移矩陣,B是控制輸入矩陣,u(k-1)是控制輸入向量,Q是過程噪聲協方差矩陣,Z(k)是系統的觀測向量,H是觀測向量,R是觀測噪聲協方差矩陣。
使用陀螺儀數據qg和ε(q)建立時間傳遞模型如下:
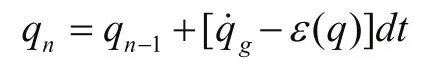
取:
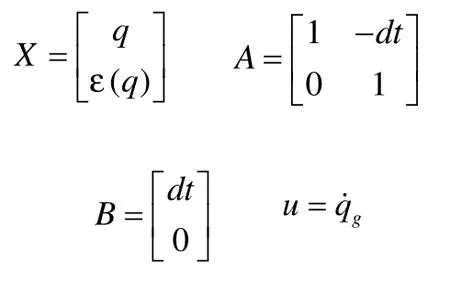
可以得到狀態矩陣方程[2]:
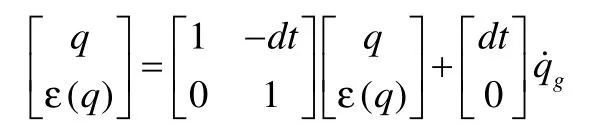
則卡爾曼濾波算法實現步驟為:
根據時間傳遞方程(12)預測k時刻的輸出:
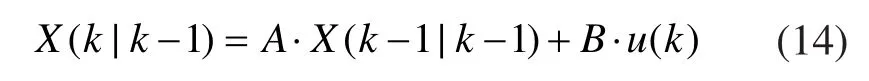
其中X(k- 1 |k- 1 )為上一時刻的最優輸出。
計算k時刻預測輸出協方差矩陣:
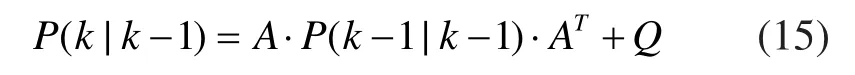
更新k時刻修正增益矩陣:
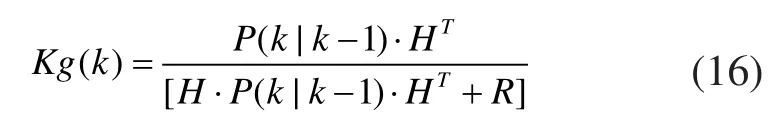
根據觀測方程(13)修正預測矩陣:
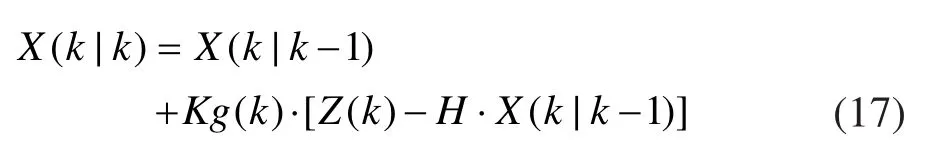
更新最優預測輸出的協方差矩陣:
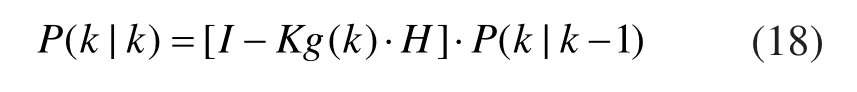
3 實驗分析
互補濾波最為簡單,基于高通與低通濾波器,構成設計準則來修正姿態;梯度下降則以偏差函數的負梯度為校正準則,使其以最快下降方向進行校正;卡爾曼濾波以狀態空間為基礎,從時間傳遞方程和測量方程出發,得出考慮各種隨機誤差在內的最佳線性估計,如圖4所示,為實時角度采樣輸出。

圖4 三種算法輸出對比
從圖中可以看到,當姿態在迅速變化時,三種算法的估計輸出幾乎重疊在一起,此時陀螺儀對姿態更新起主導作用,加速度的修正效果可以忽略。在姿態變化較為平緩階段,三種算法對姿態修正的差異才凸顯出來,這也體現了在不同修正準則下的輸出差異,但最終估計輸出都會收斂于某一穩定值。
[1]高鐘毓.慣性導航系統技術[M].北京:清華大學出版社,2012.
[2]王帥,魏國.卡爾曼濾波在四旋翼飛行器姿態測量中的應用[J].兵工自動化,2011,01:73-74,80.
[3]梁延德,程敏,何福本,李航.基于互補濾波器的四旋翼飛行器姿態解算[J].傳感器與微系統,2011,11:56-58,61.
[4]胡慶.基于STM32單片機的無人機飛行控制系統設計[D].南京航空航天大學,2012.
[5]譚廣超.四旋翼飛行器姿態控制系統的設計與實現[D].大連理工大學,2013.
[6]Bachmann, E.R., et al.“Orientation tracking for humans and robots using inertial sensors.” Computational Intelligence in Robotics and Automation, 1999.CIRA’99.Proceedings.1999 IEEE International Symposium on.IEEE,1999.
[7]Madgwick,Sebastian OH,Andrew JL Harrison, and Ravi Vaidyanathan.“Estimation of IMU and MARG orientation using a gradient descent algorithm.”Rehabilitation Robotics (ICORR), 2011 IEEE International Conference on.IEEE, 2011.
[8]Fresk, Emil,and George Nikolakopoulos.“Full quaternion based attitude control for a quadrotor.” Control Conference (ECC),2013 European.IEEE,2013.

