水下排氣速度與溫度場的氣液兩相流數值模擬

劉慧開，張勸華，趙小龍，王星宇，楊 立

(1.海軍后勤部，北京 100036; 2.海軍裝備部，北京 100036;3.海軍工程大學動力工程學院，武漢 430033)

水下航行器在通氣管航態下，需要將發動機產生的高溫廢氣排入海水中，廢氣進入海水將破裂成大小不一的氣泡，氣泡與海水混合形成具有復雜結構的氣液兩相流。為了掌握水下航行器通氣管航行時水下排氣的熱特征，有必要對氣泡在海水中的運動特性以及氣泡與海水的氣液兩相流進行深入研究。當連續地將發動機廢氣排放到液體中去，由于氣體自身的壓力與周圍環境壓力的不平衡以及氣液交界面上的表面張力等作用，氣體將破裂成大小不一的氣泡，在浮力力作用下，氣泡將向上浮升。上升的氣泡誘導周圍的液體向上運動，形成氣泡羽流流動［1-3］。對于氣泡羽流的研究，國內外都開展了一些研究工作，但還很不成熟。1996年哈爾濱工程大學張文平［4］等利用攝像機拍攝和重放技術，觀察研究了柴油機水下排氣從管口到水面氣液兩相流動狀態以及管口氣泡形成、上浮和破碎的過程。發現整個兩相流動狀態可明顯的分為氣泡形成、自由氣泡、氣泡云以及水面噴涌4 個區域。氣泡羽流的運動場通常可以劃分為3 個區域:形成區、形成后區和表面流區。在形成區，氣流破碎成氣泡，并與環境液體混和，羽流寬度和軸線流速快速增長; 而形成后區羽流寬度和軸線流速的增加要緩慢得多; 在液體表面附近，羽流轉向水平方向流動，形成具有垂向速度梯度的表面流區［5］。早期，國內外對氣泡羽流的研究主要集中在實驗研究和積分理論分析階段［6，7］。近年來，對氣泡羽流的數值研究逐漸增多，采用的數值方法主要有有限差分法、有限分析法和混合有限分析法。1994年林永明［8］等采用有限差分法對氣泡羽流紊流場進行了數值分析和模擬，與Kobus 的實驗結果符合較好。1999年Robert［9］基于完整的兩相流模型對氣泡羽流進行了二維和三維的數值模擬。2000年武漢水利電力大學的王雙峰、槐文信［10］等從兩相流理論中已被廣泛接受的雙流體概念出發，建立了描述兩相湍流流動兩方程模型，用于均勻環境中圓形氣泡羽流的數值計算，所得結果初步證實了其正確有效性。2001年馬霞［11］等假設氣泡在水中的運動僅僅是一種紊動擴散現象，提出了一個預測圓形氣泡特性的k-ε-E湍流模型，對靜止環境中的圓形氣泡羽流場進行數值模擬，模擬結果與實測資料吻合較好。2006年重慶大學劉洪濤［12］建立了氣液兩相流動傳熱的三維穩態數學物理模型，給出了描述不同模型下的換熱及流動控制方程。2012年中國船舶研究中心的喻太君等［13］對水下沖壓發動機噴管內的氣液兩相流進行了研究。

綜上可知，前人對于靜止環境中氣泡羽流的速度場研究較多，而對于水下高溫排氣的氣液兩相流速度場和溫度場的數值模擬研究幾乎為空白。因此，有必要開展水下航行器水下高溫排氣的氣液兩相流數值模擬研究。本文通過建立水下排氣的連續性方程、動量守恒方程和能量守恒方程，采用氣液兩相流混合模型和k -ε 紊流模型，利用有限體積數值計算方法，對水下排氣的速度場和溫度場進行了研究，得到了水下排氣在海洋表面形成的溫度分布，研究成果對水下航行器排氣的紅外抑制有重要的理論和應用價值。

1 水下排氣的氣液兩相流模型

目前多相流研究通常有四種模型:Lagrangian 離散模型、歐拉模型(Eulerian Model)、VOF 模型和混合模型(Mixture Model)。模擬水下排氣與海水熱交換的速度場與溫度場時，可以采用多相流中的混合模型。

連續性方程

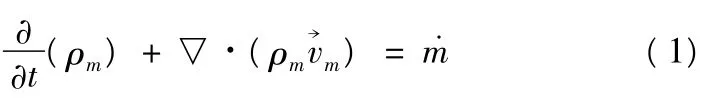
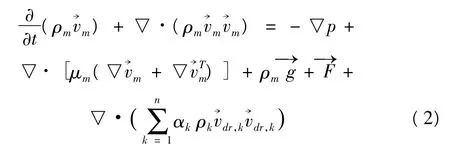
能量方程

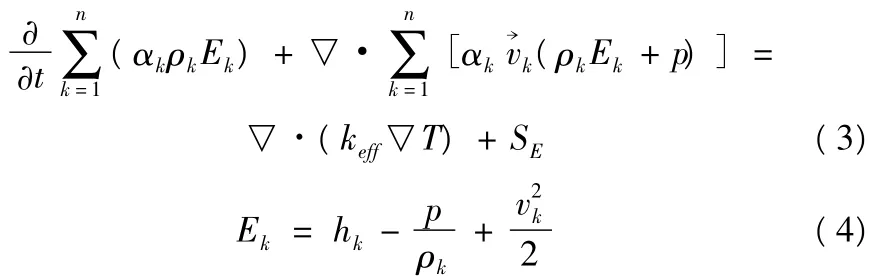
其中keff是有效熱傳導率，keff=k +kt，kt代表湍流熱傳導率。SE代表所有體積熱源。

第二相體積分數方程

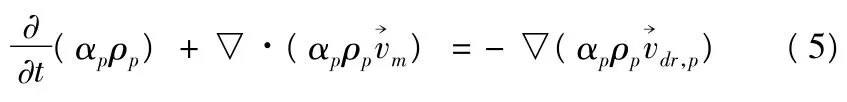
2 網格劃分與數值計算方法

由于氣液兩相流模擬計算的復雜性，有必要對水下航行器排氣口模型進行一定的簡化。由于航行器外形主要對其后的流場產生擾動，而排氣口大多布置在指揮臺上，所以外形對排氣與海水熱交換所形成的溫度場影響不是很大，本文忽略航行器外形對水下排氣的影響。假設排氣口半徑為15 cm，航行深度為排氣口距離水面4 m，計算區域海水溫度為20℃。主流場采用笛卡爾坐標系:以排氣口中心為坐標原點(0，0，0)，排氣管長0.5 m。其中y 軸正方向為尾流排氣離開艇體的方向，y 軸負方向為航行方向，z 軸正方向為海水深度方向，主流場尺寸3 m×10 m×5 m，其數值計算實體模型如圖1 所示。排氣口采用四面體網格，在y =0 面采用三角形網格結構，流場區域采用混合網格結構。通過網格無關性檢驗，計算域共生成網格1 675 608 個網格單元，其網格劃分情況如圖2 所示。

利用Fluent 軟件進行計算，通過3D 穩態分離求解器求解，重力方向為z 軸負方向，采用k-ε 紊流模型，定義海水為第一相，排氣為第二相。主相、氣相進口為速度邊界條件，出口為Outflow，其他面為壁面條件。壓力速度耦合格式為壓力隱式分裂算子(PISO)，壓力采用PRESTO 分離，動量與能量方程采用QUICK 離散格式，相體積分數采用一階離散方式。通過殘差值檢測器和兩相進出口質量流量檢測器來判斷計算是否收斂，當殘差值達到指定差值、兩相進出口質量流量趨于相等時，認為計算已經收斂。

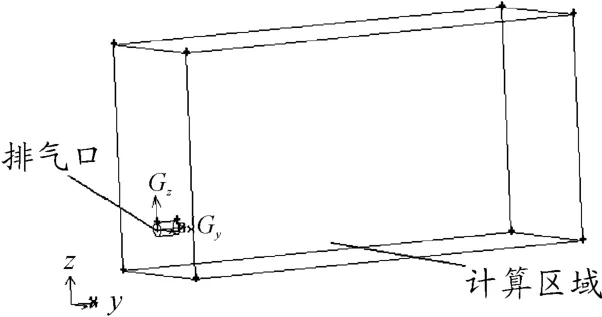
圖1 數值計算實體模型

圖2 網格劃分

3 結果分析與討論

3.1 排氣速度場

圖3 為中心軸線垂直縱截面上氣相的速度分布圖，由圖可以看出水下排出氣體在排氣口大約7.5 m 處浮出水面。排氣速度在排氣口附近最大值為45.2 m/s，在離開排氣口之后氣體速度迅速減小，至排氣口3 m 遠時排氣速度的最大值已經降至12.4 m/s，至浮出水面時氣相速度基本上已經降至海水速度4.12 m/s。

圖3 中心軸線垂直縱截面上氣相的速度分布

圖4為不同垂直截面上氣相的速度分布，從圖4 可以看出，離排氣口由遠及近，不同垂直截面上的氣相速度逐漸減小，氣相不斷向四周環境水體中擴散，氣相的分布區域逐漸增大，離排氣口不遠處的氣體擴散表現為圓形擴散，后來逐漸擴散成馬蹄形;每個截面都存在一個最大速度區域，且最大速度區域都位于擴散區域的中心區域。在y=0.6m 處，中心最大速度可達44 m/s，氣體擴散至y =9m 處，速度降至4 m/s 左右，基本上已經達到海水的速度。

圖4 不同垂直截面上氣相的速度分布

圖5為不同深度水平截面上氣相的速度分布，從圖5 可知，不同深度水平截面的氣相速度分布都類似于“流星狀”，“流星狀的尾巴”在離開排氣口的方向不斷變寬，在“流星”的根部中心區存在一個最大速度，且越靠近水面，這個速度越小，當氣相浮升至垂直高度4 m(浮出水面)時，氣相速度基本已經降至海水的速度。在z =0 處，可以看到氣體在排氣口附近的最大速度為45 m/s，之后不斷的衰減，形成明顯的速度梯度。

圖5 不同深度水平截面上氣相的速度分布

綜合圖3 ～圖5 可以發現排氣在離開排氣口之后速度迅速減小，排氣在進入環境水體之后不斷向水中擴散上浮，在浮出水面時，氣泡速度已經降至環境水體速度。

3.2 排氣溫度場

圖6 為中心軸線垂直縱截面上氣相的溫度分布，由圖6可以看出水下高溫排氣在排氣口大約7.5 m 處浮出水面，溫度降至與海水的溫差只有0.05 K。在排氣出口煙氣的溫度為400 K，在離開排氣口之后迅速減小，至排氣口2.5 m 遠時排氣溫度已經降至294 K。由于溫度差異太大，為了能更好的表現出氣體在浮出水面的溫度場，圖6 中的溫度云圖最大值為294 K，從中也可以看出氣體在400 K 降至294 K 時所經歷的時間是非常的短的。

圖6 中心軸線垂直縱截面上氣相的溫度分布

從圖7 可以看出，離排氣口由遠及近，不同垂直截面上的氣相溫度逐漸減小，氣相不斷向四周擴散，分布區域逐漸增大，離排氣口不遠處的擴散表現為圓形擴散，后來逐漸擴散成馬蹄形，且每個截面都存在一個最大溫度區域。對比圖4，我們發現雖然溫度場與速度場的變化有類似之處，但溫度場的擴散區域要明顯小于速度場擴散的區域，這說明溫度的降低速率要比速度降低的速率要快得多。水下航行器排氣在擴散至y=3 m 處時，其最大溫度已經降至僅有293.5 K。

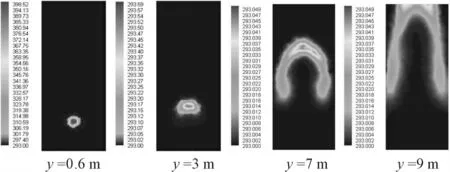
圖7 不同垂直截面上氣相的溫度分布

圖8為不同深度水平截面上氣相的溫度分布，從圖8 可知，不同深度水平截面的氣相溫度分布都類似于“流星狀”，“流星狀的尾巴”在離開排氣口的方向不斷變寬，在“流星”的根部中心區存在一個最大溫度，且越靠近水面，這個溫度越小，當氣相浮升至離排氣口4 m(浮出水面)時，氣相溫度與海水的溫度差降至0.05 K。對比圖5，我們同樣可以發現氣泡的溫度梯度要比速度梯度大很多，氣泡從400 K 降至394 K 所需要的時間是非常短的。

綜合圖6 ～圖8 可以發現:水下航行器排氣在離開排氣口之后溫度迅速降低，氣相溫度在離開排氣口水平距離3 m時，其最大溫度已經降至僅有293.5 K;排氣在進入環境水體后不斷向水中擴散上浮，在浮出水面時，氣泡溫度已經降至與環境溫度水體相差0.05 K;氣相擴散的范圍在剛離開排氣口時基本為圓形，但是在浮出水面之后基本充滿了整個計算區域。

3.3 不同排氣溫度下的水下航行器排氣特征

在不改變其他初始條件下，改變水下航行器排氣在排氣口的初始溫度，可以發現降低水下航行器排氣在排氣口的初始溫度，可有效降低水下航行器排氣浮升至水面時與周圍海水的溫度差。初始溫度為523 K 的排氣在離開排氣口浮升至水面時，氣相與周圍海水的最大溫差為0.11 K。當初始溫度從523 K 降至400 K 時，浮升至海面時與海水的溫度差從0.11 K 降至0.05 K，進一步降低初始溫度至333 K 時，浮升至海面時與海水的溫度差將降至0.013 K。可見，降低水下航行器水下排氣口的初始溫度，可有效降低排氣浮升至水面時與周圍海水的溫度差。

圖8 不同深度水平截面上氣相的溫度分布

4 結論

運用有限體積數值計算方法對水下航行器水下排氣形成的氣泡羽流的浮升過程進行了數值模擬，得到了水下排氣形成的羽流速度場和溫度場。

在溫度均勻的海水中水下排氣羽流浮升時，氣相的速度不斷減小，最后與海水的速度大小基本相等; 在氣相速度減小的過程中，每一個縱截面都存在一個速度最大的中心區域，中心區域的形狀由圓形慢慢發展成馬蹄形。氣相速度場的水平截面區域類似于“流星狀”，且可看出明顯的速度梯度存在。

水下排氣羽流浮升時，氣相的溫度在海水中不斷降低，由出口溫度400 K 降至與海水的溫差為0.05 K;在溫度降低的過程中，每一個縱截面都存在一個溫度最大的中心區域，中心區域的形狀由圓形慢慢發展成為馬蹄形;氣相溫度場的水平截面區域也類似于“流星狀”，且可看出明顯的溫度梯度存在。與氣相的速度場，溫度場發展的區域要明顯比速度場發展的區域“要窄”。

降低水下航行器排氣的初始溫度，可有效降低排氣浮升至水面時與周圍海水的溫度差。當初始溫度從523 K 降至400 K 時，浮升至海面時與海水的溫度差從0. 11 K 降至0.05 K，進一步降低初始溫度至333 K 時，浮升至海面時與海水的溫度差將降至0.013 K。

［1］吳鳳林，Tsang G.關于氣泡羽流的研究［J］.水動力學研究與進展，1989，4(1):104-112.

［2］吳鳳林，Tsang G.三維氣泡羽流建立區流動形態的觀察［J］.力學學報，1991，23(1):1-8.

［3］Friedl M J，Fannelop T K.Bubble plumes and theirs interaction with the water surface［J］.Applied Ocean Research，2000(22):119-128.

［4］張文平，張天元，劉志剛，等.柴油機水下排氣口氣液兩相流動狀態研究［J］.內燃機工程，1996，17(3):14-18.

［5］王雙峰，槐文信，李煒.靜止均勻環境中氣泡射流特性的研究——數學模型及實驗資料的分析［J］.水科學進展，2000，11(1):25-31.

［6］Kobus H E.Proc.of 11th Conf.on coastal Eng［C］.London，ASCE.New York，p 106，1968.

［7］Fannelop T K，Sjoen K.AIAA 18th Aerospace Sci.Meeting［C］.Pasadena，CA.，1980.

［8］林永明，李煒.氣泡羽流紊流的應力代數模型及數值分析［J］.水道港口，1994，21(2):32-36.

［9］Robert F.Mudde，Oliver simonin.Two-and three-simulations of a bubble plume using a two-fluid model［J］.Engineering Science，1999，54:5061-5069.

［10］王雙峰，槐文信，李煒.靜止均勻環境中氣泡射流特性的研究——形成區及形成后區特性的數值研究［J］.水科學進展，2000，11(1):32-37.

［11］馬霞，李建中，魏文禮，等.氣泡羽流的數值模擬［J］.西安理工大學學報，2001，17(1):86-89.

［12］劉洪濤. 有內熱源熔池內的氣液兩相流流動與傳熱［D］.重慶:重慶大學，2006.

［13］喻太君，王寶壽.水下沖壓發動機噴管內兩相流動［J］.四川兵工學報，2012，33(3):4-7.