基于車內綜合聲場貢獻分析的車身板件聲振優化

靳 暢，周 鋐

(同濟大學新能源汽車工程中心，上海 201804)

?

2015242

基于車內綜合聲場貢獻分析的車身板件聲振優化

靳 暢，周 鋐

(同濟大學新能源汽車工程中心，上海 201804)

在應用聲傳遞向量技術對某商用客車的車內噪聲進行板件聲學貢獻分析的基礎上，提出了引入特征頻率計權系數和場點權重系數確定多特征頻率下對車內綜合聲場聲學貢獻量最大的關鍵車身板件的方法。接著采用中心組合設計通過最小二乘擬合建立了以關鍵板件振速和1階模態頻率為目標，板件與阻尼層厚度為變量的非線性的響應面模型，通過優化確定了變量的最佳組合。優化方案的實車試驗結果顯示車內噪聲改善效果明顯。

車身板件；聲學貢獻；聲傳遞向量；中心組合設計；響應面模型；優化

前言

汽車車身大部分由薄鋼板構成，當其受到發動機或路面不平引起的邊界載荷激勵時引起板件結構振動向車內輻射聲能形成車內噪聲，因此板件是車內結構聲[1]傳遞的一個重要環節。確定對車內關鍵位置噪聲貢獻最大的結構板件是進行車內降噪的重要前提，之后對關鍵板件的振動抑制是降低車內低頻噪聲的有效手段。文獻[2]中基于有限元法(FEM)預測了車身板件輻射引起的100～500Hz車內噪聲，但其研究中以激振器作為加載而非實際的載荷。文獻[3]和文獻[4]中采用了基于邊界元法(BEM)[5]和有限元法的聲傳遞向量(ATV)法[6]對怠速時的車身板件聲學貢獻做了相應的研究，但都只針對車內單個噪聲場點或單個問題特征頻率，無法體現板件在多個特征頻率下對整體車內聲場的聲學貢獻量。文獻[7]中以“聲學貢獻和”和“聲場總貢獻”來衡量車身板件對乘員室聲壓響應的聲學貢獻，但在板件降噪措施上并未做系統的優化分析。本文中在聲傳遞向量法分析板件聲學貢獻的基礎上，提出了引入特征頻率計權系數和場點權重系數以確定多特征頻率下車內綜合聲場聲學貢獻量最大的關鍵車身板件，并提出了基于非線性響應面模型的近似擬合來建立板件振速、1階模態頻率與板件、阻尼層厚度之間的關系，系統地優化了板件與阻尼層厚度組合以達到最佳降噪效果。

1 聲傳遞向量板件聲學貢獻

聲傳遞向量(acoustic transfer vector, ATV)法是有限元-邊界元耦合分析法的發展，聲傳遞向量ATV在場點聲壓與結構振動表面之間建立了一種對應關系，其物理意義可以理解為單元在特定頻率下的單位速度在場點上引起的聲壓值[6]。將車身板件劃分成K個有限單元，車內某場點的總聲壓p可以表示為這K個有限單元振動引起的聲壓的矢量疊加，則在某點處的聲壓為

(1)

式中：K為單元總數；ve,j(ω)為單元j的法向振速。

單元e對某場點的聲學貢獻量De是該單元振動引起的那部分聲壓pe在該點總聲壓p矢量上的投影，板件區域由k個單元劃分組成，其歸一化的聲學貢獻量為

(2)

根據聲傳遞向量法對某商用客車以70km/h的車速在粗糙路面行駛工況下進行板件聲學貢獻分析。為了反映整個車內聲場特性在駕駛員和第1～5排乘客右耳5個位置布置噪聲場點測點，試驗在半消聲室內的比利時路面底盤測功機上進行，采用LMS公司SC305數據采集系統測量噪聲，由分析軟件Test.Lab計算的A計權噪聲自功率譜如圖1所示，在43，75，188和225Hz處有明顯噪聲峰值，將其作為分析的特征頻率。建立車身的結構和聲腔模型，結構有限元模型材料參數如表1所示，車內聲腔邊界元模型和板件劃分區域見圖2。在70km/h下經過輪胎、懸架和車架傳至車身底部4個連接點(圖3)的3方向激勵力(圖4)作為模型的載荷輸入，采用LMS Virtual.Lab軟件計算聲傳遞向量后得到各特征頻率處車內各場點的板件聲學貢獻，如圖5所示。由圖可見，同一場點在不同特征頻率處的貢獻是不一樣的，甚至會有正負之差。因此應該綜合考慮板件、場點和頻率因素的不同，避免在抑制板件振動降低某一頻率聲壓響應的同時，造成另一頻率位置的噪聲惡化。

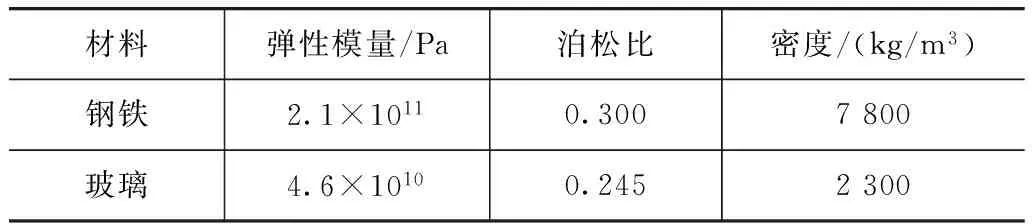
表1 車身模型主要材料參數

2 多特征頻率車內綜合聲場聲學貢獻

根據上述分析，車身板件在各特征頻率下對各場點的聲學貢獻是不同的。但可以根據場點和特征頻率在車內綜合聲場中的重要性，賦予每個場點和每個響應特征頻率不同的計權。本文中提出了一個車內整體聲學貢獻的表達式為

(3)

式中：(pc)Total為所有板件在多特征頻率車內綜合聲場下的貢獻量集；(pc)i,N為所有劃分的板件對某場點N聲壓響應中的某特征頻率i處的聲學貢獻量；n為板件貢獻量分析關心的特征頻率數量；m為場點數量；αi為每個特征頻率的計權系數，表示對特征頻率的不同重視程度；βN為第N個場點的權重系數。權重系數βN可根據在場點N處的主要特征頻率總聲壓響應占所有場點聲壓響應總和比例的大小而確定，可表示為

(4)

式中DN,i為場點N在特征頻率i下的聲壓頻率響應值。

式(3)的多特征頻率車內綜合聲場貢獻量可全面地表征板件對車內聲場整體聲學特性的影響，其量值表示該板件對車內聲場整體聲學特性貢獻量的大小。結合所研究的車輛，板件區域數量為36，n=4，m=5；對每個特征頻率都給予相同的重視程度，αi=1；βN則按式(4)計算得到，見表2。板件的整體聲學貢獻量排序結果如圖6所示，6號板件即左后頂圍區域為對車內整體聲場具有最大的聲學正貢獻量，因此需要對其進行修改優化。

表2 各場點計權系數βN

3 基于非線性響應面模型的板件振速優化

根據聲傳遞向量原理，板件的振速直接關系到車內的聲學特性，抑制板件的振動是車內降噪的有效手段。根據研究[8]，改變板件厚度和鋪設阻尼層都會對振速產生抑制作用。因此，通過修改關鍵板件和阻尼層厚度來優化結構的聲振特性以降低車內噪聲。

3.1 非線性響應面模型

在結構優化之前首先要明確板件振速與厚度間定性和定量的關系。對于鋪設阻尼層的車身板件復合結構所涉及的結構振動優化問題一般是非線性且非常復雜的，采用仿真計算的方法費時費力，為降低優化的復雜程度，減少計算時間，近似擬合是一個有效的方法，響應面法(response surface method, RSM)能夠很好地表述目標函數和約束函數與設計變量之間的非線性關系[9-10]。其基本思想是通過有限的輸入變量和輸出響應的樣本點進行回歸分析，擬合出解析表達式來代替真實響應面。

一般地，系統的響應量y與設計變量(x1,x2,…,xk)可以表示為

y=g(x1,x2,…,xk)+ε

(5)

通過有限樣本點而得的系統函數f(x1,x2,…,xk)也可寫為

y=f(x1,x2,…,xk)+ε

(6)

式中ε表示響應的觀測誤差或噪聲。f(x1,x2,…,xk)是對g(x1,x2,…,xk)的近似，對于非線性的響應關系，用2階多項式表示為

(7)

響應面法建模的關鍵是模擬的準確性和效率，利用實驗設計可以用有限的數值計算樣本點保證較高的響應面模型精度。基于中心組合設計(CCD)[11]的2階響應面建模使用較少的實驗點，并能保證回歸分析的精度。通過實驗設計擬合出響應面模型，從而確定設計變量的最佳組合，結構的優化問題就變成一個純粹的數學優化問題，其流程如圖7所示。

以關鍵板件的單元最大振速vn和阻尼復合板件的1階模態頻率ω作為響應面模型的分析目標，選取板件厚度t1和阻尼層厚度t2作為設計變量。關鍵板件6號左后頂圍的基礎厚度為0.8mm，考慮到工程實際中板件厚度可改變的范圍，表3列出了設計變量t1和t2的初始取值。將設計變量轉換為無量綱的編碼以方便進行中心組合實驗，新的無量綱變量為

(8)

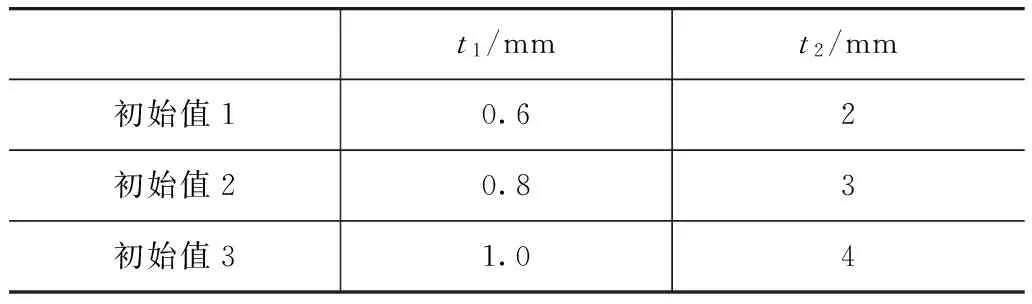
表3 設計變量初始值

原設計變量初始值轉變為如表4的3種無量綱初始水平。

采用兩個變量一個中心點的中心組合設計方法，選取9個數值仿真樣本點進行回歸分析。對應左后頂圍關鍵板件在車身有限元模型相應位置以體(Solid)單元模擬瀝青材料阻尼層，設置其彈性模量為71MPa，密度為1 200kg/m3，泊松比為0.45，阻尼材料的損耗因子取常數0.8。用公共節點法來模擬阻尼與板件的粘接作用。以70km/h下車身工作力邊界載荷添加20～300Hz的激勵計算9組設計變量下關鍵板件的vn和ω，結果如表5所示。

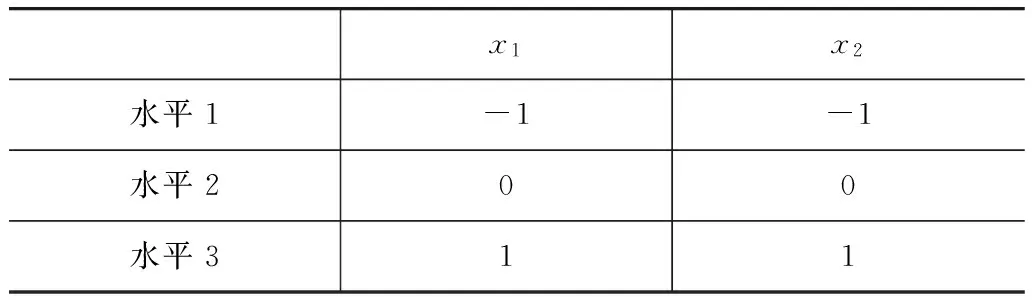
表4 中心組合設計的設計變量取值

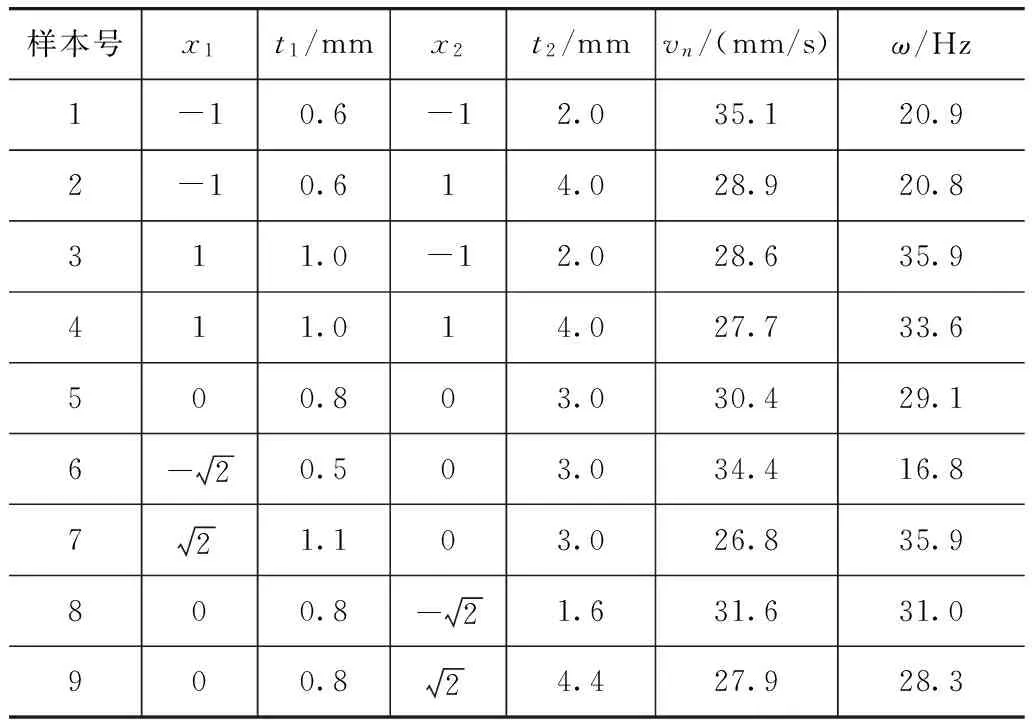
表5 中心組合設計的數值計算樣本

取得了分析目標和設計變量的樣本數據后，就可進行回歸分析，確定它們之間的定量關系，建立響應面模型。考慮到目標與變量之間關系較為復雜，因此采用式(7)的二階多項式來擬合響應面。多項式中的各項系數可用基于最小二乘法的回歸分析來確定[12]，未知系數β的解為

(9)

對于二次多項式，有

X=[1,x1,…,xn,x12,x1x2,…,x1xn,…,xn2]T

未知系數的解為

(10)

式中：n為樣本點總數；k為設計變量數。

以中心組合設計結合最小二乘法得到板件振速2階多項式響應面擬合為

vn= 31.13-2.34x1-1.53x2+1.07x1x2-

0.21x12-1.14x22

(11)

板件1階模態頻率2階多項式響應面擬合為

ω= 29.14+6.84x1-0.77x2-0.54x1x2-

1.46x12+0.21x22

(12)

為檢驗所得的響應面模型的正確性，在設計變量取值范圍內任意取3組設計變量組合(x1,x2)進行數值計算，并與響應面模型的計算結果相比較并計算偏差，結果如表6和表7所示。可以看出，結果偏差都在3%以內，證實響應面模型能較真實地反映阻尼復合板件的響應特性。

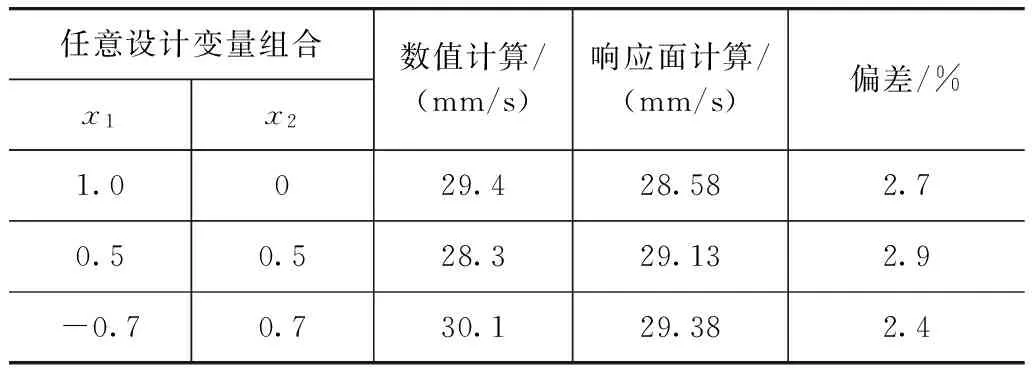
表6 板件最大振速vn數值計算與響應面計算結果對比

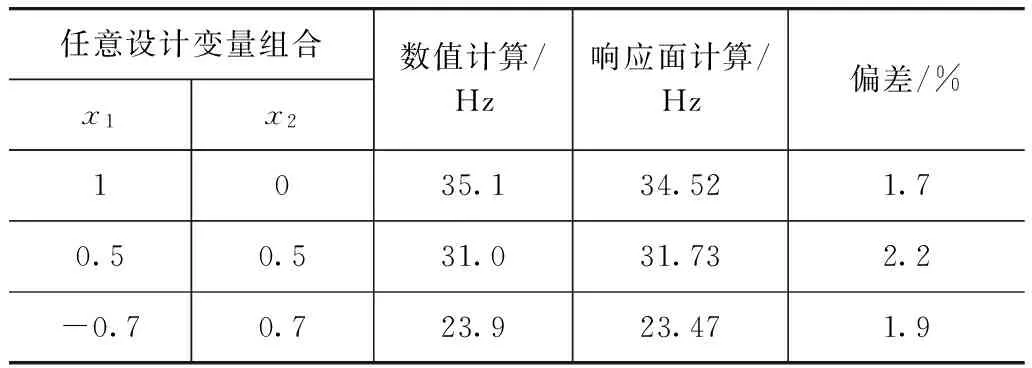
表7 板件1階模態頻率ω數值計算與響應面計算結果對比

圖8和圖9直觀地顯示了分析目標響應面模型的圖形。可以看出，當板件厚度一定且較薄時(接近-1)阻尼復合板件的振速隨阻尼層厚度的增加而降低；當板件厚度較厚時(接近1)振速隨阻尼厚度先升高后降低；當阻尼層厚度一定時，振速隨基層厚度的增加而快速下降。1階模態頻率隨板件厚度的減小而迅速降低，同時板件厚度對1階模態頻率的影響要遠大于阻尼厚度。可以看到，設計變量的變化對分析目標的影響是復雜的，因此需要確定變量的最佳組合來優化阻尼復合板件結構，從而達到減振降噪的目的。

3.2 板件振速優化

建立響應面模型的最終目的就是找出變量在設計范圍內對分析目標的最優點，板件振速是影響其向車內輻射噪聲的主要因素，因此將其作為優化的目標。而1階模態頻率直接反映了板件的結構剛度，應保證優化后不低于原狀態1階模態頻率，將其作為約束條件之一。另外，考慮到輕量化的需求，阻尼復合后的板件質量也不能過大，將其設為不高于原質量的50%作為另一個約束條件。關鍵板件基礎厚度為0.8mm，質量為8.1kg，面積為1.267m2，1階模態頻率為32.7Hz。優化設計的變量為板件厚度x1和阻尼厚度x2。由此建立如下的優化模型：

(13)

式(13)的數學模型屬于帶約束的最小化優化問題，采用MATLAB的fmincon優化函數[13]進行求解。

整個優化函數的詳細表達式為

(14)

令初始值x1=0，x2=0，優化求解得

(15)

根據式(9)將無量綱的變量轉換為實際厚度得到：

(16)

根據工程實際，取板件厚度為整數t1=0.9mm后，由響應面模型計算得到的板件振速vn=29.7625mm/s。這就是考慮了板件1階模態和板件質量約束條件下的厚度最優組合。

4 實車試驗驗證

針對上文的優化結果對實車進行方案實施并試驗。改變左后頂圍區域板件厚度為0.9mm并鋪設瀝青阻尼層，厚度2mm，如圖10所示。按照優化前相同的運行工況和場點布置進行車內噪聲試驗，由于是考察車內多個場點改善的綜合效果，在此引入一個綜合性的指標體現措施前后的差別：

(17)

式中：psyn為車內多場點的綜合噪聲指標；pN(ω)為場點N的噪聲頻譜。

圖11為板件優化前后車內多場點綜合噪聲頻譜的對比，表8列出了優化前后4個特征頻率下以及總噪聲的變化，圖12為每個場點總聲壓級的變化。可以看出，改善的效果明顯。因此，本文中提出的基于車內綜合聲場聲學貢獻分析的車身板件聲振優化方法是有效的。

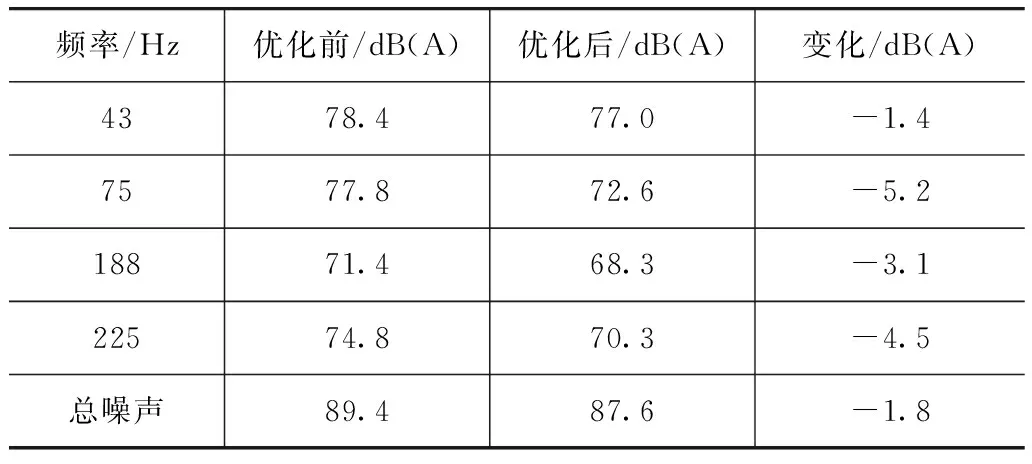
頻率/Hz優化前/dB(A)優化后/dB(A)變化/dB(A)4378.477.0-1.47577.872.6-5.218871.468.3-3.122574.870.3-4.5總噪聲89.487.6-1.8

5 結論

(1) 在采用聲傳遞向量法分析板件聲學貢獻的基礎上，提出了引入特征頻率計權系數和場點權重系數來確定多特征頻率下對車內綜合聲場聲學貢獻最大的關鍵車身板件。

(2) 提出基于響應面法尋求板件優化的目標。建立了以關鍵板件振速與1階模態頻率為目標、板件和阻尼厚度為變量的非線性響應面模型。該模型顯示，當板件厚度一定且較薄時阻尼復合板件的振速隨阻尼層厚度的增加而降低；當板件厚度較厚時振速隨阻尼厚度先升高后降低；當阻尼層厚度一定時，振速隨基層厚度的增加而快速下降。1階模態頻率隨板件厚度的減小而迅速降低，同時板件厚度對1階模態頻率的影響要遠大于阻尼厚度。

(3) 以板件振速最小化為目標，1階模態頻率和質量為約束條件確定了板件與阻尼厚度的最優組合。實車試驗結果顯示優化方案對各特征頻率和各場點的車內噪聲改善明顯。因此，本文中所提出的基于車內綜合聲場的響應面板件優化是有效可行的，為車身板件的減振降噪提供了一種較為完整、系統的優化方法。

[1] 龐劍,湛剛,何華.汽車噪聲與振動[M].北京:北京理工大學出版社,2006:312-319.

[2] Teik C Lim. Automotive Panel Noise Contribution Modeling Based on Finite Element and Measured Structural-acoustic Spectra[J]. Applied Acoustics,2000,60:505-519.

[3] 趙靜,周鋐,梁映珍,等.車身板件振動聲學貢獻分析與優化[J].機械工程學報,2010,46(24):96-100.

[4] 王二兵,周鋐,徐剛,等.基于車身板件聲學貢獻分析的聲振優化[J].江蘇大學學報,2012,33(1):25-29.

[5] 靳曉雄,張立軍.汽車噪聲的預測與控制[M].上海:同濟大學出版社,2004.

[6] 李增剛,詹福良.Virtual. Lab Acoustics聲學仿真計算高級應用實例[M].北京:國防工業出版社,2010.

[7] 韓旭,林海東,郭永進,等.基于壁板聲學貢獻分析的轎車乘員室聲場降噪研究[J].上海交通大學學報,2008,42(8):1254-1258.

[8] 梁新華.汽車車身薄壁件阻尼復合結構振動-聲學分析與優化[D].上海:上海交通大學,2007.

[9] 王永菲,王成國.響應面法的理論與應用[J].中央民族大學學報(自然科學版),2005(3):236-240.

[10] Roux W J, Stander N, Haftka R T. Response Surface Approximations for Structural Optimization[J]. Int J Numer Methods Eng,1998,3(42):517-534.

[11] 陳立周.穩健設計[M].北京:機械工業出版社,2000.

[12] 邱秩兵.實驗設計與數據處理[M].安徽:中國科學技術大學出版社,2008:185.

[13] 曹衛華,郭正.最優化方法及MATLAB實現[M].北京:化學工業出版社,2005:78-89.

Vibro-acoustic Optimization of Vehicle Body Panels Basedon Overall Interior Noise Contribution Analysis

Jin Chang & Zhou Hong

CleanEnergyAutomotiveEngineeringCenter,TongjiUniversity,Shanghai201804

Acoustic transfer vector technique is applied to an analysis on panel acoustic contribution to the interior noise of a commercial bus. Based on the analysis, a scheme is proposed of introducing weighting coefficients for characteristic frequencies and field points to determine the dominant body panels having the most acoustic contribution to overall interior sound field. Then central composite design and least square fitting are adopted to build a nonlinear response surface model with the vibration velocity of key panels and the 1st order modal frequency as objective and the thicknesses of panels and damping layers as design variables, and an optimum combination of variables is determined by optimization in the end. The results of real vehicle test with optimized scheme demonstrate an apparent noise improvement effect.

vehicle body panel; acoustic contribution; acoustic transfer vector; central composite design; response surface model; optimization

原稿收到日期為2014年5月19日，修改稿收到日期為2014年8月4日。