基于數據融合和改進MUGM（1，m，w）的導彈裝備故障預測

趙建忠，徐廷學，葉 文，張 磊

（1．海軍航空工程學院兵器科學與技術系，山東煙臺264001；2．海軍航空工程學院科研部，山東煙臺264001）

基于數據融合和改進MUGM（1，m，w）的導彈裝備故障預測

趙建忠1，徐廷學1，葉 文1，張 磊2

（1．海軍航空工程學院兵器科學與技術系，山東煙臺264001；2．海軍航空工程學院科研部，山東煙臺264001）

針對現代導彈裝備系統組成復雜、結構關系模糊、特征參數獲取不完整和不確定，造成其故障預測實現困難的問題，借鑒數據融合技術和灰色預測理論，提出了一種基于數據融合和改進多因素新陳代謝不等時距加權灰色預測模型（improved multi-variables metabolism unequal interval weighted grey model，IMUGM（1，m，w））的導彈裝備故障預測方法。首先，通過引入加權因子w的方式建立多因素不等時距加權灰色預測模型（UGM（1，m，w）），再通過初始值改進、殘差修正、新陳代謝思想相結合的方式對模型進行改進；然后以特定個體的歷史監測數據為基準，計算同類產品和特定個體的相應預測值及其與特定個體性能退化數值的Euclid距離，并根據Euclid距離確定隸屬度權值，基于加權思想建立特定個體的性能退化模型，最后結合實時監測數據依次更新性能退化數據、Euclid距離、隸屬度權值和性能退化模型，實現導彈裝備故障預測，實例仿真及分析驗證了方法的有效性。

多因素；灰色預測模型（GM（1，1））；多因素不等時距加權灰色預測模型（UGM（1，m，w））；數據融合

0 引 言

為了更好地制定導彈裝備精確維修保障計劃，降低維修保障費用，提高戰備完好率、任務成功率，最大限度地避免因裝備故障而導致的安全事故，迫切需要開展故障預測研究。文中導彈裝備主要是指導彈地面保障設備，以導彈測試設備、計量設備、監控設備等精密儀器設備為主，其系統組成復雜，結構關系模糊，特征參數獲取往往是不完整和不確定的，這成為故障預測實現的難點。灰色系統理論為“少數據”、“貧信息”、“不確定性”導彈裝備故障預測提供了一種新的途徑，是當前故障預測的一種有效方式。但在GM（1，1）模型的基礎上，仍存在一些需要優化或改進的地方［1］。首先，GM（1，1）模型通常選取第一個數據作為初始值，根據模型原理可知，這樣會降低模型的精度；其次，常見的GM（1，1）模型及其改進型大都基于等時距建立的，而導彈裝備故障預測實踐中，由于種種原因可能致數據缺失，呈現非等間隔期的狀態數據，這就大大限制了GM（1，1）模型的適用范圍，且等時距是不等時距的一個特例。因此，建立不等時距的灰色預測模型（unequal interval grey model，UGM（1，1））具有重要的現實意義。當前處理不等時距主要有以下3種方法：一是插值法。該方法由于人為主觀性太強，預測精度不高［2］。二是生成新數列法。該種方法由于在生成新數據列時，要以數據列差值與時間差的線性關系為前提，模型的邏輯性相對較差［34］。三是傳統UGM（1，1）模型法。該方法彌補了前兩種方法的不足，且計算簡便，精度較高［5-6］。另外，在導彈裝備故障過程中，故障發展、發生的影響因素較多，且這些因素大都存在內在的聯系，有時幾個指標或參數一起才能反映裝備的狀態。因此，很多情況下導彈裝備故障的預測是一種多因素故障預測［7］。文獻［8］建立了一種多因素灰色預測模型，文獻［9- 10］擴展了等間距構造方式，建立了多因素不等時距灰色預測模型（multi-variables unequal interval grey model，UGM（1，m）），但這些模型的背景值構造方式都是緊鄰均值法，這就導致在數據序列變化較大時預測誤差較大的問題；還有，我們注意到在預測實施過程中，隨著時間的推移，舊數據的信息有效性將逐漸降低，而新數據則包含大量的趨勢信息。一些學者提出了多種新陳代謝灰色預測模型，進一步提高了預測精度［11］；當灰色預測模型未達到精度要求時，需要進行殘差修正。傅里葉變換為殘差修正提供了一個很好的數學工具，可補償系統的隨機誤差，提高預測精度。除了研究導彈裝備故障預測的建模問題之外，還有如何增加輸入數據樣本量的問題，可以考慮充分利用同類型裝備在相同環境下的性能退化數據，因為它們具有同源相近性特點。

結合導彈裝備保障實際，為充分利用同類型裝備的性能退化數據，提高灰色模型的預測精度，提出一種基于數據融合和改進多因素新陳代謝不等時距加權灰色預測模型（improved multi-variables metabolism unequal interval weighted grey model，IMUGM（1，m，w））相結合的預測方法。在UGM（1，m）模型的基礎上，通過引入加權因子w的方式重新構造背景值，通過初始值優化、殘差修正和新陳代謝思想進一步提高灰色模型預測精度，通過隸屬度加權法來融合不同輸入條件下的預測結果，以便進一步提高預測精度。

1 問題描述

假設導彈裝備的工作負荷相對穩定，其電流、電壓、功率等特征參數y會隨著運行時間t呈現單調遞增或遞減的變化趨勢，當y達到失效閾值η時裝備發生故障。把第i個裝備的第j次測量時刻記為tij（i＝1，2，…，p；j＝1，2，…，n），對應的監測值記為yij，共測量nij次，并且已經獲取d個同類型裝備的性能退化數據，則第i個裝備的性能退化數據為

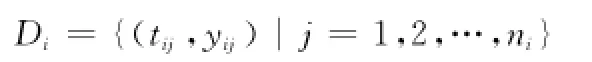
記特定裝備Z的eZ次歷史測量數據為

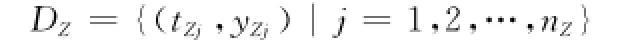
基于同類型導彈裝備的性能退化數據Di（i＝1，2，…，p）和特定導彈裝備Z的歷史測量數據DZ建立Z的性能退化軌跡模型，即y與t之間的函數關系為

通過求解η＝fZ（T），預測Z的故障時間T。將Z的監測數據（t，yZ）代入式（1），實現故障預測模型的及時更新，再重新進行預測。

2 IMUGM（1，m，w）模型建立

在UGM（1，m）模型的基礎上，通過引入加權因子w的方式建立多因素不等時距加權灰色預測模型UGM（1，m，w），再通過初始值優化、殘差修正和新陳代謝方式進一步改進，建立了IMUGM（1，m，w）模型。

2.1 初始值的改進

運用灰色自適應模型思想，對UGM（1，1）模型中的初始值選取方式進行改進。設能實現最佳預測效果的模型初始值為x（0）i（t1）＋ci，ci為一個未知優化量。則白化微分方程的時間響應函數變為

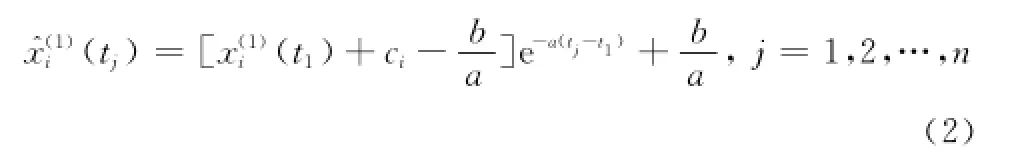
對于優化量ci，可通過使生成序列預測值的誤差在最小二乘意義下最小來求解［12］，即

為了使U（ci）最小，令求偏導得

式中

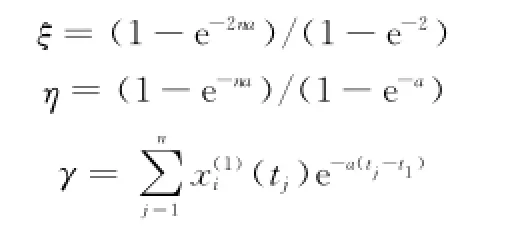
2.2 模型建立

把間距作為乘子，對原始數據列序列進行一次累加生成，可得

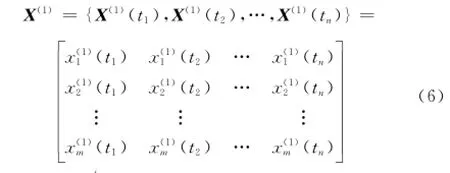
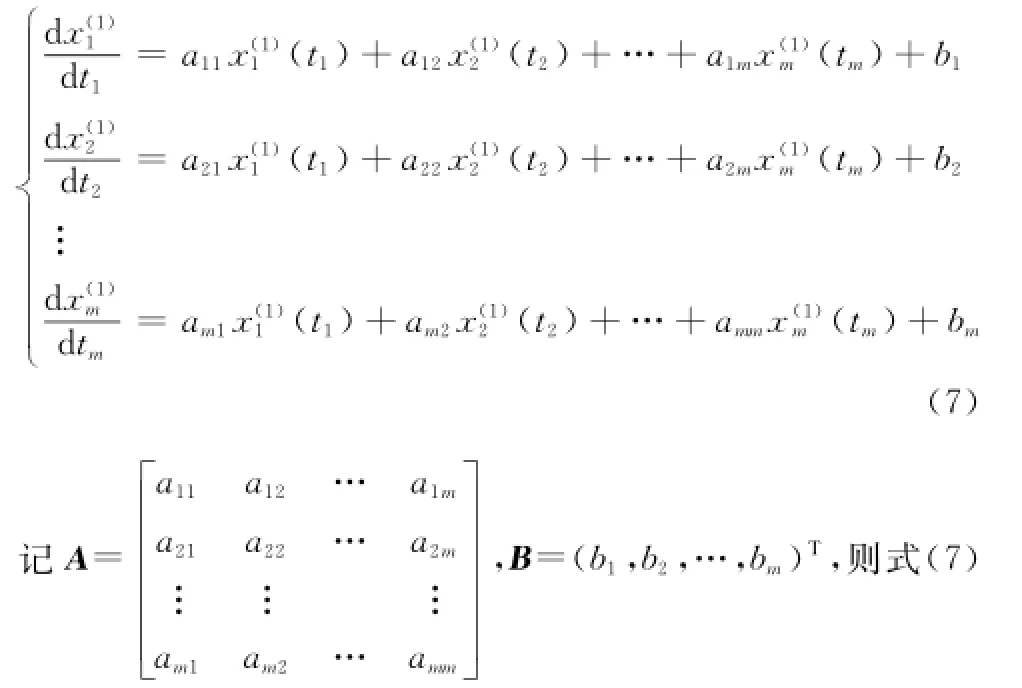
的向量表達式為

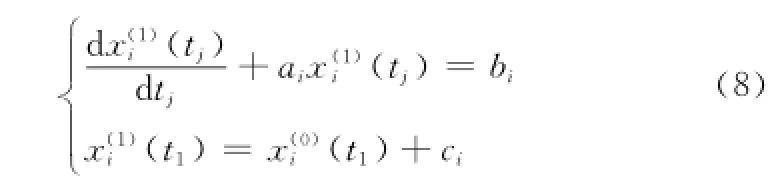
離散化上述微分方程，可得

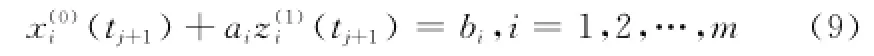
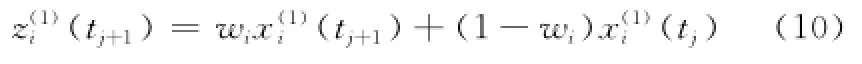
式中，wi為背景值最佳生成系數（0＜wi＜1），根據平均相對誤差最小來確定［14］。平均相對誤差表示原始值與模型預測值的誤差，表達式為

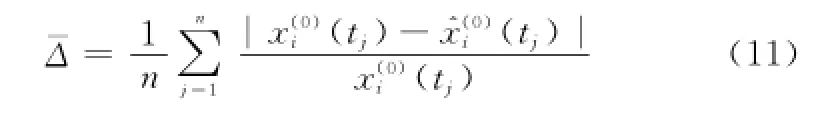
令ai＝（ai1，ai2，…，ain，bi）T，i＝1，2，…，m。用矩陣形式表示式（9），即

式中

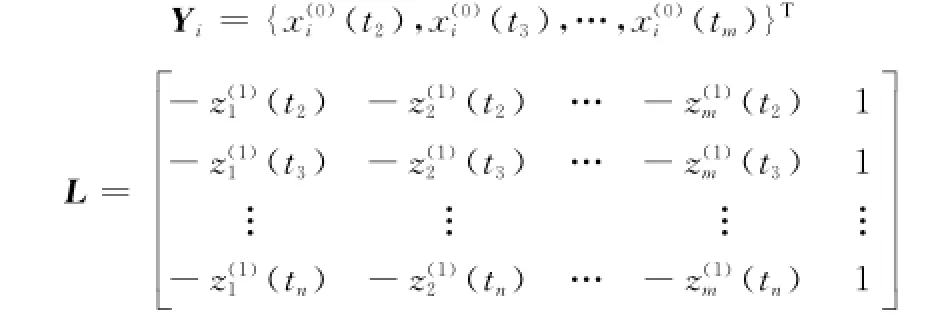
采用最小二乘法求解式（12），得

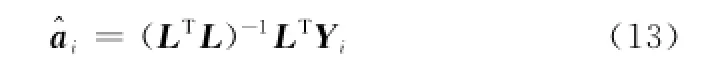
則可以得到A和B的辨識值

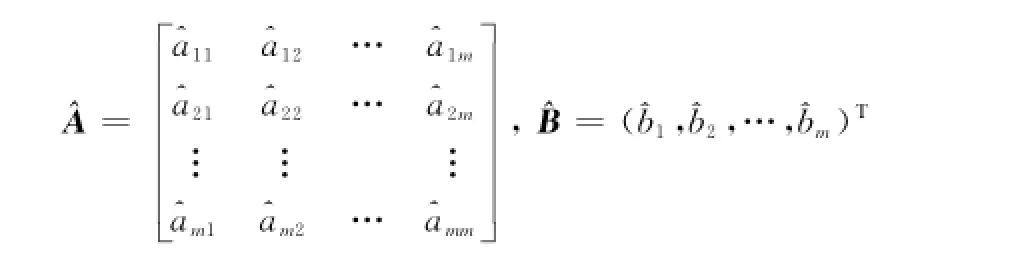
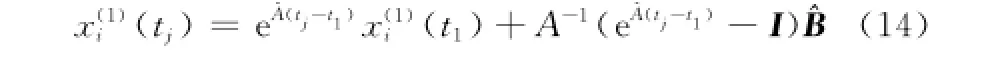
式中

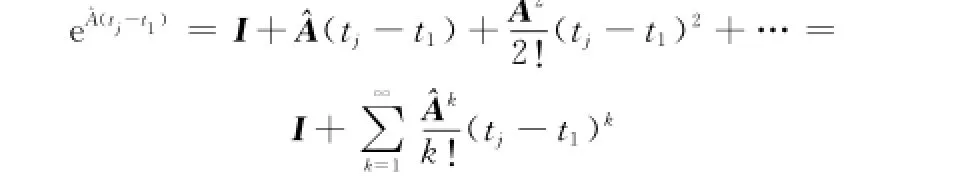
再將上式累減還原，得原始監測數據的預測值表達式：

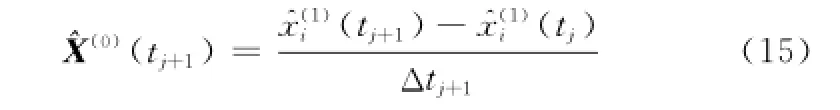
2.3 殘差修正

建立殘差序列

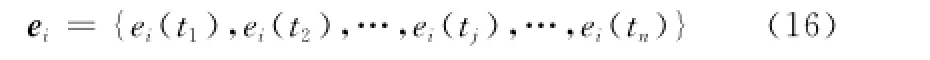
式中，ei（tj）＝（tj），i＝1，2，…，m；j＝1，2，…，n。

利用傅里葉公式將殘差序列近似表示為

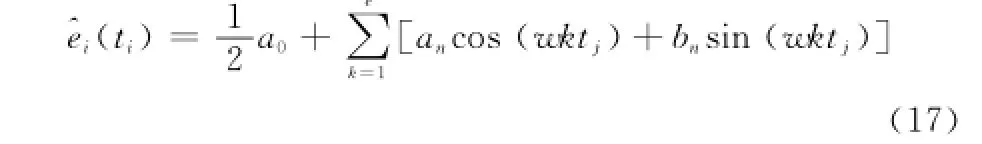
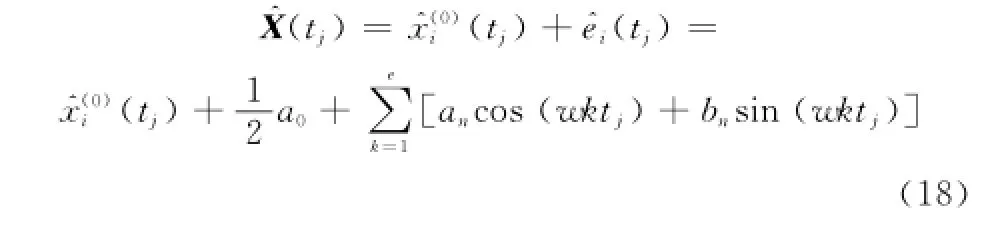
2.4 新陳代謝

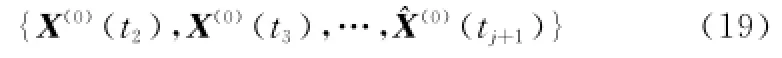
取X（1）（t2）＝X（0）（t2），執行上述式（2）～式（19）的操作，得^X（0）（tj＋2）。然后，以此類推直到最后求^X（0）（tn）。

3 基于數據融合和IMUGM（1，m，w）的導彈裝備故障預測

本文所提出的導彈裝備故障預測方法從總體上可劃分為建模和預測兩個階段，如圖1所示。先建立同類型裝備和特定裝備的IMUGM（1，m，w）故障預測模型，然后計算特定裝備對各同類型裝備的隸屬度，再運用數據融合及時建立特定裝備故障預測模型，最后結合監測數據更新隸屬度和特定裝備故障預測模型，進行故障預測。

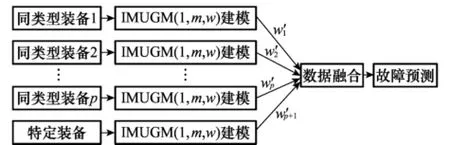
圖1 基于數據融合和IUGM（1，m，w）的導彈裝備故障預測框架圖

3.1 故障預測建模

根據IMUGM（1，m，w）模型原理，運用同類型導彈裝備的歷史監測數據yij（i＝1，2，…，p；j＝1，2，…，n），建立p個基于IMUGM（1，m，w）的故障預測模型；再運用特定裝備Z的歷史監測值yZj，建立第p＋1個基于IMUGM（1，m，w）的故障預測模型，記為｛fi（t）｜i＝1，2，…，p＋1｝。

3.2 故障預測實現

將Z的監測數據tZ分別代入p個故障預測模型，求出p個預測值向量Yi（i＝1，2，…，p）；再計算Z的監測值向量YZ與Yi的Euclid距離dZi［16］；然后根據dZi確定出Z對各同類型裝備參數值的隸屬度權值w′i，對n個故障預測模型進行加權得到特定裝備Z的故障預測模型fZ（t）；最后結合Z的監測數據［t，yZ］對tZ和YZ進行擴充，依次更新Yi，dZi和w′i，進而將fZ（t）進行及時更新，并參照η實現故障預測，將上述過程稱為隸屬度加權法（degree of membership weighted method，DWM）。

DWM的應用過程歸納為以下5個步驟。

步驟1 令s＝nZ，to＝tZs，tZ＝［tZ1，tZ2，…，tZs］T，YZ＝［yZ1，yZ2，…，yZs］T。

步驟2 將tZ代人｛fi（t）｜i＝1，2，…，p｝，算得Yi＝［fi（tZ1），fi（tZ2），…，fi（tZs）］T，i＝1，2，…，p；計算YZ與Yi的Euclid距離

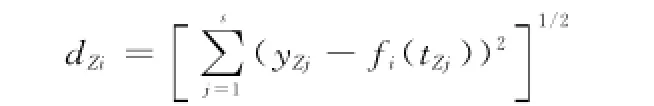
步驟3 計算Z對各同類型裝備監測參數值的隸屬度權值［17］：w′ifi（t），求解η＝fZ（T）得Z的故障發生時刻預測值T，計算故障發生時間（T－t0）。

步驟5 獲取Z的最新監測數據（t，yZ），令t0＝t，s＝s＋1，tZ＝［tz；t］，YZ＝［YZ；yZ］，轉步驟2。如果存在i，使得dZi＝0，則有w′i＝1，w′j＝0（j≠i）。

步驟4 建立Z的故障預測模型fZ（t）＝

4 案例分析

高頻模擬器裝置是雷達制導導彈檢測設備中的重要組成部分，用來產生模擬攻擊目標的距離、方位等信息的各種脈沖波形，然后再把回波信號反饋傳輸給導引頭以達到檢測導彈性能參數的目的。以某型導彈測試設備為例，它的高頻模擬器依據通訊協議，由控制器控制發出所需要的脈沖信號，然后經由高頻信號調制并進行放大，最后由天線發射出去。接收到的回波信號送給一個功率分配器，再將調制后的高頻信號送到設備的自檢接口進行自檢，其工作原理框架如圖2所示。

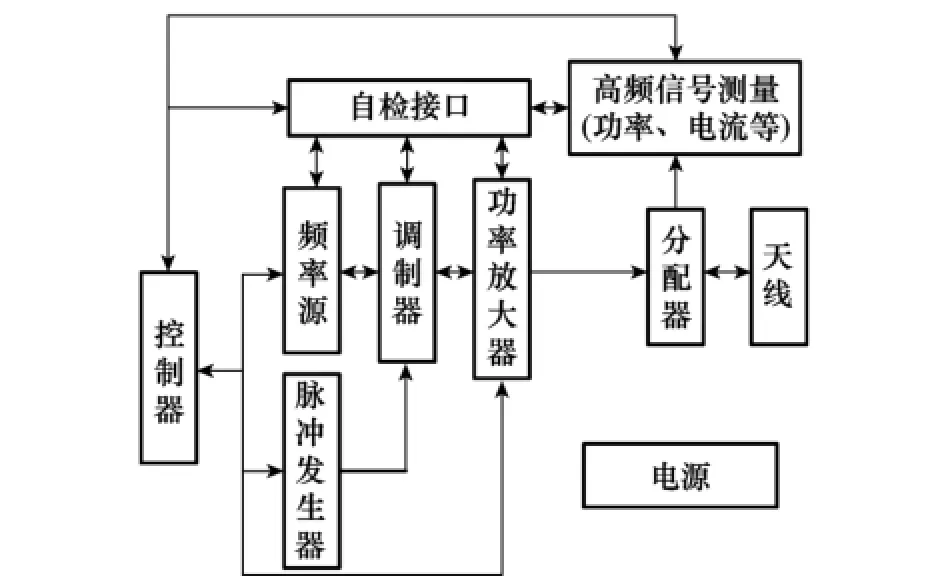
圖2 高頻模擬器原理框圖

圖2 中，功放組件是高頻模擬器的重要功能部件，它可以為導彈導引頭測試提供一定功率、頻率的信號，它的狀態正常與否直接影響著導彈測試設備的功效。功放組件在工作過程中，通常處于大功率、大電流以及高頻率工作狀態，屬于故障頻發件。在輸入一定的條件下，某型功放組件的正常工作輸出功率為70～74W，電流為2～2．6A，當超過上述工作范圍時，就會出現故障。因此，可將功放組件的輸出功率值和電流值作為該功放組件故障預測的特征量。對3套功放組件工作狀態進行監測，獲得的數據如表1所示。

4.1 模型建立

對于分析對象特定設備3，利用數據序列中從首個數據開始的前7組數據建模，后4組數據進行模型驗證。對于同類型設備1和設備2，利用數據序列中從第2個數據開始的前7組數據建模。

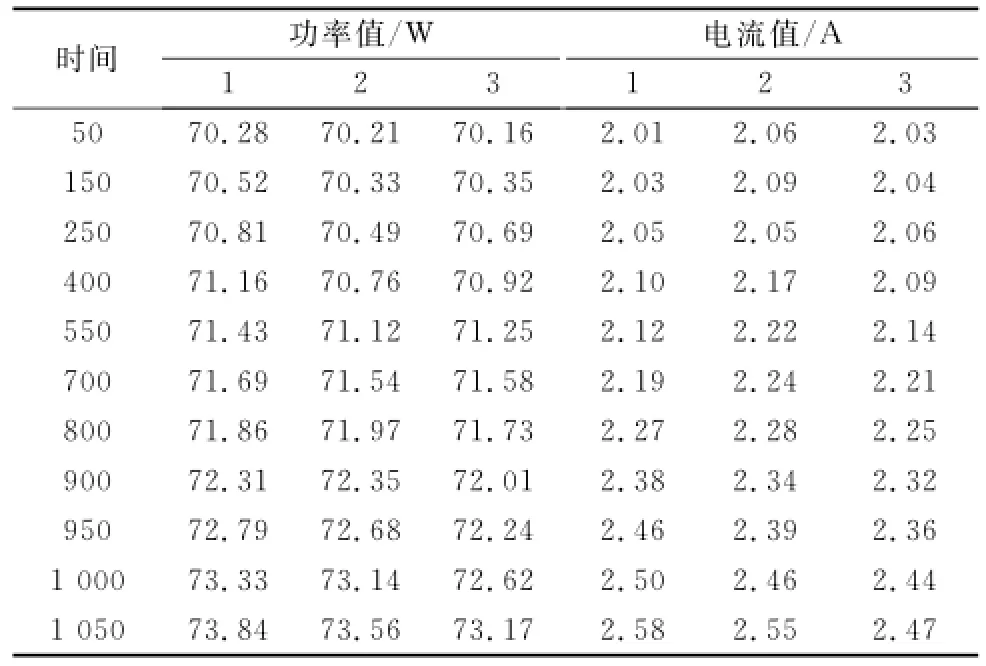
表1 某型高頻模擬器的狀態監測數據

根據表1，可將原始數據序列表示為

根據式（2）～式（19），編程計算得

同理，可以計算其他數據。

4.2 故障預測

根據Euclid距離dZi和隸屬度權值w′i的表達公式，可以編程計算得：w′11＝0.171 3，w′21＝0.287 2，w′31＝0.541 5，進而求得x＾（0）（t8）＝（72.078 1，2.308 4）。依次類推，最后求得：w′14＝0.282 2，w′24＝0.116 0，w′34＝0.601 8，x＾（0）（t11）＝（73.259 8，2.485 1）。

為了說明本文預測方法的優越性，將傳統UGM（1，m）模型、改進新陳代謝不等時距灰色預測模型（improved metabolism unequal interval grey model，IMUGM（1，1））以及IMUGM（1，m，w）與本文預測方法的預測結果進行比較分析，各預測方法或模型的預測結果分別如表2以及圖3、圖4所示，并分別以預測值（forecast，FU）、相對誤差（relative error，RPE）和平均相對誤差（meam relative error，MRE）表示。

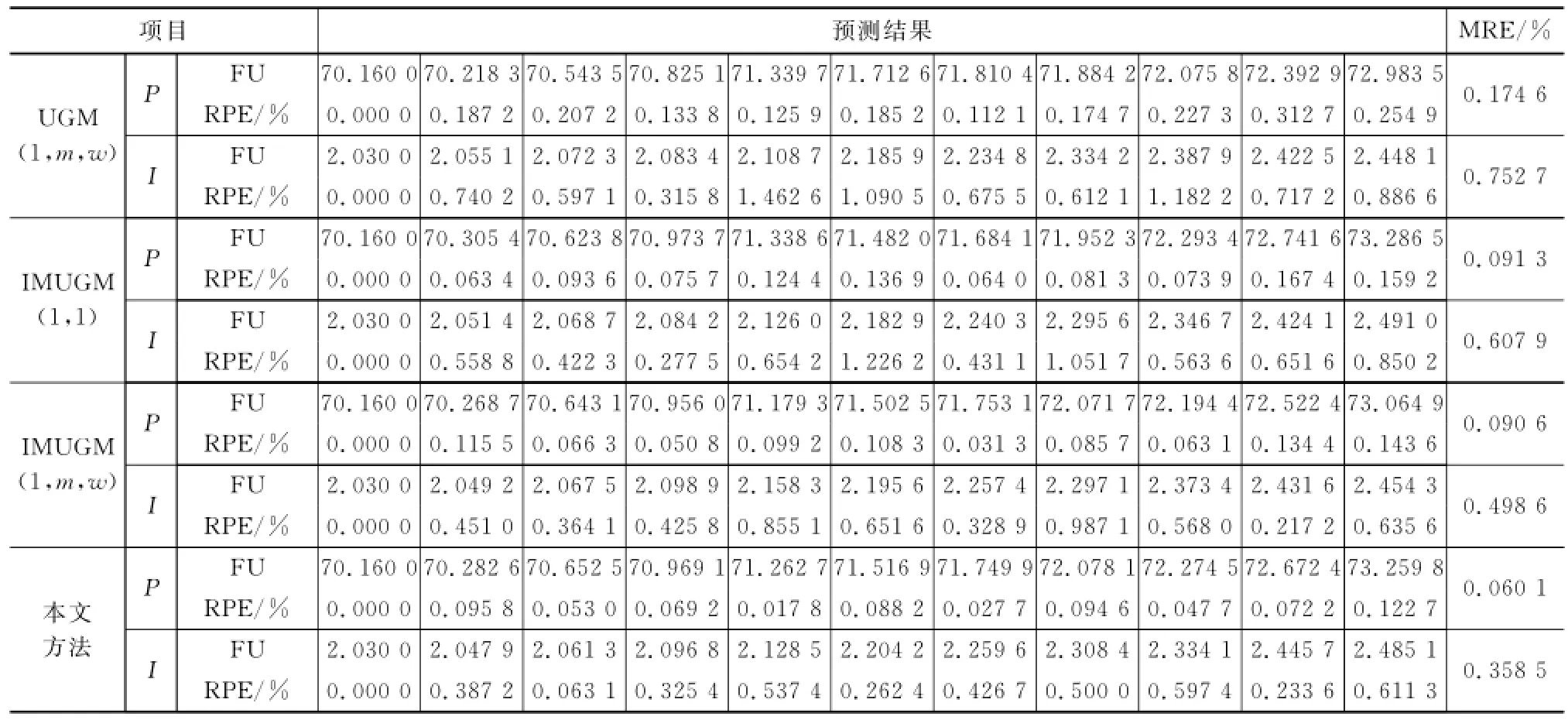
表2 不同方法的預測值及相對誤差

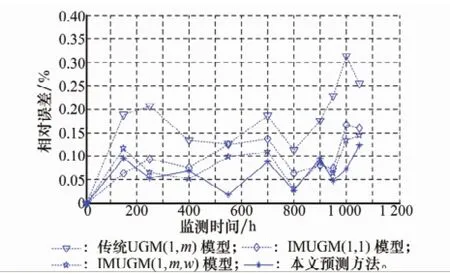
圖3 輸出功率預測結果對比圖

圖4 電流預測結果對比圖

4.3 結果分析

由表2以及圖3和圖4可知，傳統UGM（1，m）模型精度最差，IMUGM（1，m，w）模型次之，而本文方法擬合效果最好、預測精度最高。這是因為，傳統UGM（1，m）模型是最初的不等時距灰色預測模型，存在較多的缺陷；IMUGM（1，1，w）模型引入加權因子w的方式重新構造背景值，并通過初始值優化、殘差修正和新陳代謝思想對模型進行了改進；IMUGM（1，m，w）模型是在IMUGM（1，1，w）模型的基礎上，綜合利用了功放組件的多個因素之間的相關性信息；而本文中的故障預測方法在IMUGM（1，m，w）模型的基礎上，還運用數據融合技術來融合同類型設備的性能退化數據進行建模，進一步提高了預測精度。

5 結 論

由于導彈裝備屬于精密的機電設備，影響其狀態變化的因素很多，反映其狀態的參量呈現較大的波動性、動態性和隨機性，通過簡單的建模難以表達清楚。在分析當前故障預測技術和灰色系統理論發展的基礎上，提出了基于數據融合和改進不等時距加權灰色預測模型的導彈裝備故障預測方法。它通過引入加權因子w的方式重新構造背景值，解決了在數據序列變化較大時傳統UGM（1，m）模型預測誤差較大的問題，并提出了一種基于隸屬度加權法的融合同類型裝備性能退化數據的故障預測方法，充分利用了同類型裝備的性能退化數據。此外，由于多因素灰色預測模型綜合考慮了導彈裝備狀態變化對各個特征參數的影響，預測精度更高，具有廣闊的應用前景。

［1］Liu S F，Dang Y G，Fang Z G．Grey system theory and it’s application［M］．Beijing：Science Press，2004．（劉思峰，黨耀國，方志耕．灰色系統理論及其應用［M］．北京：科學出版社，2004．）

［2］Kuo H C，Wu L J．Prediction of heat-affected zone using grey theory［J］．Journal of Materials Processing Technology，2002，120（1）：151- 168．

［3］Trivedi H V，Singh J K．Application of grey system theory in the development of a runoff prediction model［J］．Biosystems Engineering，2005，92（4）：521- 526．

［4］Chen Y G，Dai W Z．Modeling research of model GM（1，1）based on improved Euler formula and its application［C］∥Proc.of the IEEE International Conference on Grey Systems and Intelligent Services，2007：416- 420．

［5］Erdal K，Ulutas B，Kaynak O．Grey system theory-based models in time series prediction［J］．Expert Systems with Applications，2010，37（2）：1784- 1789．

［6］Kumar U，Jain V K．Times series models（grey-Markov，grey model with rolling mechanism and singular spectrum analysis）to forecast energy consumption in India［J］．Energy，2010，35（4）：1709- 1706．

［7］Jan M K，Michal B．Diagnostic models of industrial processes［J］．International Journal of COMADEM，2005，8（2）：23- 29．

［8］Li J F，Dai W Z．A new approach of background value building and its application based on data interpolation and Newton-Cores formula［J］．Systems Engineering-Theory&Practice，2004，24（10）：122- 126．（李俊峰，戴文戰．基于插值和Newton-Cores公式的GM（1，1）模型的背景值構造新方法與應用［J］．系統工程理論與實踐，2004，24（10）：122- 126．）

［9］Sun N．Prediction of transformer fault by non-equidistance multivariable grey model［J］．Electric Power Science and Engineering，2010，26（9）：27- 30．（孫娜．基于非等間距灰色多變量模型預測變壓器故障［J］．電力科學與工程，2010，26（9）：27- 30．）

［10］Wang F X．Multivariable non-equidistance GM（1，m）model and its application［J］．Systems Engineering and Electronics，2007，29（3）：388- 390．（王豐效．多變量非等間距GM（1，m）模型及其應用［J］．系統工程與電子技術，2007，29（3）：388- 390．）

［11］Chen S，Li Z．Grey target theory based equipment condition monitoring and wear mode recognition［J］．Wear，2006，260（4／5）：438- 449．

［12］Huang S J，Huang C L．Control of an inverted pendulum using grey prediction model［J］．IEEE Trans.on Industry Application，2000，36（2）：452 458．

［13］Zhou S J，Lai Z K，Zang D Y，et al．Weighted grey prediction model and implement of its computation［J］．Geomatics and Information Science of Wuhan University，2002，27（5）：451-455．（周世健，賴志坤，藏德彥，等．加權灰色預測模型及其計算實現［J］．武漢大學學報（信息科學版），2002，27（5）：451- 455．）

［14］Huang S J，Huang C L．Control of an inverted pendulum using grey prediction model［J］．IEEE Trans.on Industry Application，2000，36（2）：452- 458．

［15］Xie N M．Discrete grey forecasting model and its optimization［J］．Application Mathematical Modeling，2009，33（2）：1173- 1186．

［16］Liu R Y．Euclid distance with weight and its applications［J］．Application of Statistics and Management，2002，21（5）：1216- 1225．

［17］Zhang L L，Yin J X，Hou Z C．Ecological drought evaluation function of Baiyangdian based on fuzzy membership degree［J］．Journal of Hohai University（Natural Sciences），2010，34（3）：1143- 1149．

Missile equipment fault forecast based on data fusion and improved MUGM（1，m，w）

ZHAO Jian-zhong1，XU Ting-xue1，YE Wen1，ZHANG Lei2
（1.Department of Ordnance Science and Technology，Naval Aeronautical and Astronautical University，Yantai 264001，China；2.Department of Scientific Research，Naval Aeronautical and Astronautical University，Yantai 264001，China）

In order to overcome the difficulty of modern missile equipment fault forecast，which is induced by the complexity of system composition，fuzziness of configuration connection and incomplete and uncertaint character parameters，according to data fusion technique and grey forecast theory，a new forecast method based on data fusion and improved multi-variables metabolism unequal interval weighted grey model（IMUGM（1，m，w）model）is proposed．Firstly，multi-variables unequal interval weight grey model（MUGM（1，m，w）model）is built by introducing weight gene and optimized by initial value optimization，residual error correction and metabolism．Then the specific individual’s historical measure data are used as the benchmark，and the same kind of products and the specific individual’s corresponding forecast values are calculated using IMUGM（1，m，w）models．The Euclid distances are used to determine degree of membership，so the individual’s performance degradation model is built on the basis of the degree-of-membership weighted method．Finally，the measurement data，Euclid distances，degree of membership and performance degradation model are updated with real-time measurement data．The proposed method is applied to fatigue crack growth data，and the experimental results validate the validity．The result of simulating practical missile equipment fault forecast and analysis validates the validity．

multi-variables；grey forecast model（GM（1，1））；multi-variables unequal interval weighted grey model（UGM（1，m，w））；date fusion

V 237

A

10．3969／j．issn．1001-506X．2015．04．17

趙建忠（1978-），男，講師，博士，主要研究方向為裝備綜合保障理論與技術、航空軍械保障工程。E-mail：zjznavy＠163．com

徐廷學（1962-），男，教授，博士，主要研究方向為裝備綜合保障。E-mail：xtx1962＠163．com

葉 文（1979-），男，副教授，博士，主要研究方向為航空軍械保障。E-mail：yw1979＠163．com

張 磊（1980-），男，碩士，主要研究方向為導彈裝備技術保障。E-mail：zhl1980＠163．com

1001-506X（2015）04-0832-06

2013- 12- 26；

2014- 05- 06；網絡優先出版日期：2014- 07- 30。

網絡優先出版地址：http：／／w ww．cnki．net／kcms／detail／11．2422．TN．20140730．1051．004．html

軍隊科研項目資助課題